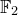1. Introduction
1.1 Background
A real structure on a complex manifold
![]() $X$
is an anti-holomorphic involution, that is, a diffeomorphism
$X$
is an anti-holomorphic involution, that is, a diffeomorphism
satisfying
![]() $\sigma^2=\textrm {id}_X$
and
$\sigma^2=\textrm {id}_X$
and
![]() $\sigma ^*I=-I$
, where
$\sigma ^*I=-I$
, where
![]() $I$
denotes the complex structure on
$I$
denotes the complex structure on
![]() $X$
. In this paper, a real variety (or
$X$
. In this paper, a real variety (or
![]() $\mathbb {R}$
-variety) refers to a pair
$\mathbb {R}$
-variety) refers to a pair
![]() $(X, \sigma )$
consisting of a complex manifold
$(X, \sigma )$
consisting of a complex manifold
![]() $X$
and a real structure
$X$
and a real structure
![]() $\sigma$
on it. If there is no risk of confusion, we may omit the reference to
$\sigma$
on it. If there is no risk of confusion, we may omit the reference to
![]() $\sigma$
in our notation. The real locus of
$\sigma$
in our notation. The real locus of
![]() $(X, \sigma )$
, denoted by
$(X, \sigma )$
, denoted by
![]() $X(\mathbb {R})$
, is defined to be the fixed locus of the involution
$X(\mathbb {R})$
, is defined to be the fixed locus of the involution
![]() $\sigma$
. When
$\sigma$
. When
![]() $X(\mathbb {R})\neq \emptyset$
, it is a differentiable submanifold of
$X(\mathbb {R})\neq \emptyset$
, it is a differentiable submanifold of
![]() $X$
, and its real dimension is equal to the complex dimension of
$X$
, and its real dimension is equal to the complex dimension of
![]() $X$
. These concepts can be extended to the setting of complex analytic spaces.
$X$
. These concepts can be extended to the setting of complex analytic spaces.
In algebraic geometry, a real form of a complex algebraic variety
![]() $X$
is an algebraic variety
$X$
is an algebraic variety
![]() $X_0$
defined over
$X_0$
defined over
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
![]() $X\simeq X_0\times _{\textrm {Spec} \mathbb {R}} \textrm {Spec}\mathbb {C}$
as
$X\simeq X_0\times _{\textrm {Spec} \mathbb {R}} \textrm {Spec}\mathbb {C}$
as
![]() $\mathbb {C}$
-varieties. For a quasi-projective complex variety
$\mathbb {C}$
-varieties. For a quasi-projective complex variety
![]() $X$
, there is a natural bijection between the set of its real forms (up to
$X$
, there is a natural bijection between the set of its real forms (up to
![]() $\mathbb {R}$
-isomorphism) and the set of real structures on
$\mathbb {R}$
-isomorphism) and the set of real structures on
![]() $X(\mathbb {C})$
(up to conjugation); see [Reference HartshorneHar77, Exercise II.4.7]. In this paper, we will use both perspectives interchangeably. Except in Section 11,
$X(\mathbb {C})$
(up to conjugation); see [Reference HartshorneHar77, Exercise II.4.7]. In this paper, we will use both perspectives interchangeably. Except in Section 11,
![]() $X$
denotes the complex space
$X$
denotes the complex space
![]() $X(\mathbb {C})$
.
$X(\mathbb {C})$
.
As was included as the 16th problem in Hilbert’s famous list [Reference Hilbert and ProblemeHil00], real algebraic geometry has a central theme of studying the topology of the real locus
![]() $X(\mathbb {R})$
and its relation to the complex geometry of
$X(\mathbb {R})$
and its relation to the complex geometry of
![]() $X$
. This subject predates complex algebraic geometry, as seen in the classical Harnack theorem from 1876 [Reference HarnackHar76], which states that a real plane curve of degree
$X$
. This subject predates complex algebraic geometry, as seen in the classical Harnack theorem from 1876 [Reference HarnackHar76], which states that a real plane curve of degree
![]() $d$
has at most
$d$
has at most
![]() $\frac {d^2-3d+4}{2}$
connected components. In 1882, Klein [Reference KleinKle82] found an intrinsic generalization of this theorem to any genus-
$\frac {d^2-3d+4}{2}$
connected components. In 1882, Klein [Reference KleinKle82] found an intrinsic generalization of this theorem to any genus-
![]() $g$
compact Riemann surface equipped with a real structure, showing that the real locus can have at most
$g$
compact Riemann surface equipped with a real structure, showing that the real locus can have at most
![]() $g+1$
connected components (which are circles). This result on curves is generalized to arbitrary dimensions through the Smith–Thom inequality; see, for example, [Reference Degtyarev, Itenberg and KharlamovDIK00, §1.2] and [Reference MangolteMan20, Theorem 3.3.6].
$g+1$
connected components (which are circles). This result on curves is generalized to arbitrary dimensions through the Smith–Thom inequality; see, for example, [Reference Degtyarev, Itenberg and KharlamovDIK00, §1.2] and [Reference MangolteMan20, Theorem 3.3.6].
Theorem 1.1 (Smith–Thom inequality). Let
![]() $(X,\sigma )$
be a real variety of dimension
$(X,\sigma )$
be a real variety of dimension
![]() $n$
. We have the following inequality for the total
$n$
. We have the following inequality for the total
![]() $\mathbb {F}_2$
-Betti numbers:
$\mathbb {F}_2$
-Betti numbers:
Here for a topological space
![]() $W$
, its total
$W$
, its total
![]() $\mathbb {F}_2$
-Betti number is
$\mathbb {F}_2$
-Betti number is
![]() $b_*(W, \mathbb {F}_2):=\sum _{i} b_i(W, \mathbb {F}_2)$
with
$b_*(W, \mathbb {F}_2):=\sum _{i} b_i(W, \mathbb {F}_2)$
with
![]() $b_i(W, \mathbb {F}_2):=\dim _{\mathbb {F}_2} H^i(W, \mathbb {F}_2)$
.
$b_i(W, \mathbb {F}_2):=\dim _{\mathbb {F}_2} H^i(W, \mathbb {F}_2)$
.
When equality in (1) holds, we call
![]() $(X, \sigma )$
a maximal real variety (or M-variety). Maximal real varieties have attracted significant research interest over the decades. Intriguing properties are uncovered for those real varieties, such as the Rokhlin congruence theorem for even-dimensional maximal smooth projective real varieties:
$(X, \sigma )$
a maximal real variety (or M-variety). Maximal real varieties have attracted significant research interest over the decades. Intriguing properties are uncovered for those real varieties, such as the Rokhlin congruence theorem for even-dimensional maximal smooth projective real varieties:
![]() $\chi _{\mathrm {top}}(X(\mathbb {R}))\equiv \operatorname {sgn}(X) \mod 16$
; see [Reference MangolteMan20, Theorem 3.4.2]. On the other hand, providing a rich supply of examples of maximal real varieties has always been an important task, but constructing them has proven challenging, particularly in higher dimensions. For curves and surfaces, the construction problem has been extensively studied, and for certain class of varieties (e.g. K3 surfaces) even a classification up to real deformation is partially achieved; we refer to [Reference MangolteMan20] for an account. However, the available methods for constructing higher-dimensional maximal real varieties have been somewhat limited. Viro’s combinatorial patchworking for hypersurfaces [Reference Itenberg and ViroIV07] is currently the most powerful method. We refer to [Reference Brugallé and SchaffhauserBS22, §3] for a recent summary.
$\chi _{\mathrm {top}}(X(\mathbb {R}))\equiv \operatorname {sgn}(X) \mod 16$
; see [Reference MangolteMan20, Theorem 3.4.2]. On the other hand, providing a rich supply of examples of maximal real varieties has always been an important task, but constructing them has proven challenging, particularly in higher dimensions. For curves and surfaces, the construction problem has been extensively studied, and for certain class of varieties (e.g. K3 surfaces) even a classification up to real deformation is partially achieved; we refer to [Reference MangolteMan20] for an account. However, the available methods for constructing higher-dimensional maximal real varieties have been somewhat limited. Viro’s combinatorial patchworking for hypersurfaces [Reference Itenberg and ViroIV07] is currently the most powerful method. We refer to [Reference Brugallé and SchaffhauserBS22, §3] for a recent summary.
1.2 Results
The main objective of this paper is to present a new type of construction that produces new maximal varieties from existing ones. Our approach can be loosely described as ‘taking moduli spaces of objects on a maximal variety’, where objects can refer to algebraic cycles (or flags of such), vector bundles, coherent sheaves (or complexes of such) and so on. We have achieved the following concrete results.
-
(i) We provide a short and computation-free proof of Brugallé–Schaffhauser’s result (Theorem5.3) that, for coprime integers
 $n\gt 0$
and
$n\gt 0$
and
 $d$
, the moduli space
$d$
, the moduli space
 $M_C(n, d)$
of stable vector bundles of rank
$M_C(n, d)$
of stable vector bundles of rank
 $n$
and degree
$n$
and degree
 $d$
on a maximal curve
$d$
on a maximal curve
 $C$
is a maximal variety, and vice versa if
$C$
is a maximal variety, and vice versa if
 $C(\mathbb {R})\neq \emptyset$
. The same result holds for the moduli spaces of stable parabolic bundles with full flag type (Corollary 5.5).
$C(\mathbb {R})\neq \emptyset$
. The same result holds for the moduli spaces of stable parabolic bundles with full flag type (Corollary 5.5). -
(ii) By adapting our new proof in (i) to the context of Higgs bundles, we establish the maximality of the moduli space
 $H_C(n, d)$
of stable Higgs bundles over a maximal curve
$H_C(n, d)$
of stable Higgs bundles over a maximal curve
 $C$
of coprime rank and degree (Theorem6.3).
$C$
of coprime rank and degree (Theorem6.3). -
(iii) If a real variety
 $X$
has maximal Hilbert square
$X$
has maximal Hilbert square
 $X^{[2]}$
and
$X^{[2]}$
and
 $X(\mathbb {R})\neq \emptyset$
, then
$X(\mathbb {R})\neq \emptyset$
, then
 $X$
itself, its Hilbert cube
$X$
itself, its Hilbert cube
 $X^{[3]}$
and the nested Hilbert schemes
$X^{[3]}$
and the nested Hilbert schemes
 $X^{[1,2]}$
and
$X^{[1,2]}$
and
 $X^{[2,3]}$
are all maximal (Theorem7.3).
$X^{[2,3]}$
are all maximal (Theorem7.3). -
(iv) For a maximal real smooth cubic 3-fold, all the smooth (nested) Hilbert schemes are maximal (Theorem7.5). On the contrary, for a maximal real smooth cubic 4-fold, its Hilbert square is never maximal (Theorem11.12).
-
(v) If a smooth projective maximal
 $\mathbb {R}$
-surface
$\mathbb {R}$
-surface
 $S$
satisfies
$S$
satisfies
 $H^1(S, \mathbb {F}_2)=0$
and
$H^1(S, \mathbb {F}_2)=0$
and
 $S(\mathbb {R})$
is connected, then the
$S(\mathbb {R})$
is connected, then the
 $n$
th punctual Hilbert scheme
$n$
th punctual Hilbert scheme
 $S^{[n]}$
is maximal, for any
$S^{[n]}$
is maximal, for any
 $n\gt 0$
(Theorem8.1). This result applies, for example, to maximal
$n\gt 0$
(Theorem8.1). This result applies, for example, to maximal
 $\mathbb {R}$
-rational real surfaces (Corollary 8.6), to some surfaces of Kodaira dimension 1 (Corollary 8.9) and to smooth projective real surfaces with Tate motives (Theorem11.10).
$\mathbb {R}$
-rational real surfaces (Corollary 8.6), to some surfaces of Kodaira dimension 1 (Corollary 8.9) and to smooth projective real surfaces with Tate motives (Theorem11.10). -
(vi) For integers
 $r\gt 0, c_1, c_2$
with
$r\gt 0, c_1, c_2$
with
 $ \gcd \left (r, c_1, \frac {c_1(c_1+1)}{2}-c_2\right )=1$
, the moduli space of stable sheaves on
$ \gcd \left (r, c_1, \frac {c_1(c_1+1)}{2}-c_2\right )=1$
, the moduli space of stable sheaves on
 $\mathbb {P}^2_{\mathbb {R}}$
with rank
$\mathbb {P}^2_{\mathbb {R}}$
with rank
 $r$
and first and second Chern classes
$r$
and first and second Chern classes
 $c_1$
and
$c_1$
and
 $c_2$
is also maximal (Theorem9.1).
$c_2$
is also maximal (Theorem9.1). -
(vii) For a Poisson
 $\mathbb {R}$
-surface
$\mathbb {R}$
-surface
 $S$
satisfying the K-maximality condition (Definition 4.1) and a generic real ample line bundle
$S$
satisfying the K-maximality condition (Definition 4.1) and a generic real ample line bundle
 $H$
, the moduli spaces
$H$
, the moduli spaces
 $M_H(S, v)$
of
$M_H(S, v)$
of
 $H$
-stable sheaves with Mukai vector
$H$
-stable sheaves with Mukai vector
 $v$
on
$v$
on
 $S$
are maximal (Theorem10.1). This result applies, for example, to
$S$
are maximal (Theorem10.1). This result applies, for example, to
 $\mathbb {R}$
-rational maximal real Poisson surfaces (Corollary 10.2).
$\mathbb {R}$
-rational maximal real Poisson surfaces (Corollary 10.2).
In all of our results, we implicitly include the claim that the moduli space (or Hilbert scheme) under consideration has a natural real structure. The maximality referred to in the conclusion is with respect to this real structure.
1.3 Motives
In addition to providing examples of maximal varieties obtained via moduli constructions, another important aspect of the paper is to highlight, in Section 11, the significant role played by motive and its equivariant formality in the study of maximal real varieties.
We observe that the maximality of real algebraic varieties is a motivic property, determined solely by the homological real motive with
![]() $\mathbb {F}_2$
-coefficients of the real variety (Definition 11.2). As a consequence (Corollary 11.7), if a real algebraic variety
$\mathbb {F}_2$
-coefficients of the real variety (Definition 11.2). As a consequence (Corollary 11.7), if a real algebraic variety
![]() $Y$
has motive contained in the tensor subcategory generated by the motives of some maximal varieties
$Y$
has motive contained in the tensor subcategory generated by the motives of some maximal varieties
![]() $\{X_i\} _{i}$
(in which case we say that
$\{X_i\} _{i}$
(in which case we say that
![]() $Y$
is motivated by the
$Y$
is motivated by the
![]() $X_i$
's), then
$X_i$
's), then
![]() $Y$
is also maximal. From this motivic perspective, many results established in this paper can be explained or reproved. Further details can be found in Section 11.
$Y$
is also maximal. From this motivic perspective, many results established in this paper can be explained or reproved. Further details can be found in Section 11.
1.4 Branes in hyper-Kähler manifolds
On a hyper-Kähler manifold
![]() $X$
, an anti-holomorphic involution
$X$
, an anti-holomorphic involution
![]() $\sigma$
is referred to as an (ABA) or (AAB) brane involution,Footnote
1
and its fixed locus, which is precisely the real locus
$\sigma$
is referred to as an (ABA) or (AAB) brane involution,Footnote
1
and its fixed locus, which is precisely the real locus
![]() $X(\mathbb {R})$
, is known as an (ABA) or (AAB) brane in
$X(\mathbb {R})$
, is known as an (ABA) or (AAB) brane in
![]() $X$
, as defined in [Reference Baraglia and SchaposnikBS14] (see also [Reference Franco, Jardim and MenetFJM19, §2.3]). Regarding to the Smith–Thom inequality,
$X$
, as defined in [Reference Baraglia and SchaposnikBS14] (see also [Reference Franco, Jardim and MenetFJM19, §2.3]). Regarding to the Smith–Thom inequality,
![]() $X(\mathbb {R})$
is called a maximal brane if the real variety
$X(\mathbb {R})$
is called a maximal brane if the real variety
![]() $(X, \sigma )$
is maximal. Our aforementioned result (ii) on Higgs bundles provides examples of maximal (ABA) or (AAB) branes in hyper-Kähler manifolds of arbitrarily high dimensions, which are non-compact but have a complete hyper-Kähler metric. Another example of maximal brane in a non-compact hyper-Kähler manifold is provided by the cotangent bundle of a maximal
$(X, \sigma )$
is maximal. Our aforementioned result (ii) on Higgs bundles provides examples of maximal (ABA) or (AAB) branes in hyper-Kähler manifolds of arbitrarily high dimensions, which are non-compact but have a complete hyper-Kähler metric. Another example of maximal brane in a non-compact hyper-Kähler manifold is provided by the cotangent bundle of a maximal
![]() $\mathbb {R}$
-variety.
$\mathbb {R}$
-variety.
However, the situation is more intriguing for compact hyper-Kähler manifolds (see [Reference BeauvilleBea83] and [Reference HuybrechtsHuy99] for generalities of such manifolds). On the one hand, in (complex) dimension 2, maximal real K3 surfaces and abelian surfaces exist and have been thoroughly studied; see [Reference KharlamovKha76], [Reference SilholSil89, Chapters IV, VIII]. On the other hand, Kharlamov and Răsdeaconu [Reference Kharlamov and RăsdeaconuKR23] recently discovered that the Hilbert squares of maximal real K3 surfaces and Fano varieties of lines of maximal cubic 4-folds are never maximal (see Remark 7.4). This leads to a challenging question: does there exist maximal (ABA) or (AAB) branes in compact hyper-Kähler manifolds of dimension
![]() $\geqslant 4?$
$\geqslant 4?$
1.5 Structure of the paper
-
– Section 2 provides a brief overview of equivariant cohomology, Atiyah’s
 $\textrm {KR}$
-theory and Chern classes.
$\textrm {KR}$
-theory and Chern classes. -
– Section 3 covers fundamental operations that preserve maximality of real varieties, including products (Lemma 3.1), symmetric powers (Theorem3.2), projective bundles or flag bundles (Proposition 3.3), blow-ups (Proposition 3.5), flips and flops (Remark 3.6), generically finite surjection with odd degree (Proposition 3.8), the Albanese variety and the Picard variety (Proposition 3.10), the intermediate Jacobian of a maximal real cubic 3-folds (Proposition 3.14), etc. These results are either documented in the literature or well-known to experts.
-
– Section 4 introduces
 $c_1$
-maximality and K-maximality, discusses their relation to maximality and provides some examples.
$c_1$
-maximality and K-maximality, discusses their relation to maximality and provides some examples. -
– The main results are presented and proved in Sections 5–10; please refer to the table of contents.
-
– In Section 11, basic notions of motives are recalled and the notion of equivariant formality is introduced. Maximality is reformulated in the context of motives, and Section 11.4 revisits the results from a motivic point of view and provides some more applications.
2. Preliminaries
Throughout the paper, we denote
![]() $G:=\operatorname {Gal}(\mathbb {C}/\mathbb {R})$
, which is a cyclic group of order 2.
$G:=\operatorname {Gal}(\mathbb {C}/\mathbb {R})$
, which is a cyclic group of order 2.
2.1 Equivariant cohomology
Let
![]() $X$
be a complex variety or manifold. A real structure
$X$
be a complex variety or manifold. A real structure
![]() $\sigma$
on
$\sigma$
on
![]() $X$
gives rise to an action of
$X$
gives rise to an action of
![]() $G$
on
$G$
on
![]() $X$
, where the non-trivial element of
$X$
, where the non-trivial element of
![]() $G$
acts by
$G$
acts by
![]() $\sigma$
, an anti-holomorphic involution.
$\sigma$
, an anti-holomorphic involution.
Let
![]() $BG$
be the classifying space of
$BG$
be the classifying space of
![]() $G$
and
$G$
and
![]() $EG$
its universal cover. These spaces are unique up to homotopy equivalence. In the case where
$EG$
its universal cover. These spaces are unique up to homotopy equivalence. In the case where
![]() $G\simeq \mathbb {Z}/2\mathbb {Z}$
, we can use the infinite-dimensional real projective space
$G\simeq \mathbb {Z}/2\mathbb {Z}$
, we can use the infinite-dimensional real projective space
![]() $\mathbb {R}\mathbb {P}^{\infty }$
(respectively, infinite-dimensional sphere
$\mathbb {R}\mathbb {P}^{\infty }$
(respectively, infinite-dimensional sphere
![]() $\mathbb {S}^{\infty }$
), endowed with the weak topology, as a model for
$\mathbb {S}^{\infty }$
), endowed with the weak topology, as a model for
![]() $BG$
(respectively,
$BG$
(respectively,
![]() $EG$
).
$EG$
).
Let
![]() $X_G:=X\times ^G EG$
be the Borel construction, where
$X_G:=X\times ^G EG$
be the Borel construction, where
![]() $\times ^{G}$
denotes the quotient by the (free) diagonal action of
$\times ^{G}$
denotes the quotient by the (free) diagonal action of
![]() $G$
. Given a coefficient ring
$G$
. Given a coefficient ring
![]() $F$
(such as
$F$
(such as
![]() $\mathbb {Z}$
or
$\mathbb {Z}$
or
![]() $\mathbb {F}_2$
), we denote by
$\mathbb {F}_2$
), we denote by
the equivariant cohomology ring with
![]() $F$
-coefficients.
$F$
-coefficients.
We note that there is a natural fiber sequence
which gives rise to the Leray–Serre spectral sequence:
Here, the left-hand side is the group cohomology and
![]() $H^q(X, \mathbb {F}_2)$
is viewed as a
$H^q(X, \mathbb {F}_2)$
is viewed as a
![]() $G$
-module.
$G$
-module.
More generally, if we have a
![]() $G$
-module
$G$
-module
![]() $\mathcal {F}$
, such as
$\mathcal {F}$
, such as
![]() $\mathbb {Z}(r):=(\sqrt {-1})^r\mathbb {Z}$
, which is the
$\mathbb {Z}(r):=(\sqrt {-1})^r\mathbb {Z}$
, which is the
![]() $G$
-module with underlying group
$G$
-module with underlying group
![]() $\mathbb {Z}$
upon which the non-trivial element of
$\mathbb {Z}$
upon which the non-trivial element of
![]() $G$
acts by
$G$
acts by
![]() $(-1)^r$
(hence only the parity of
$(-1)^r$
(hence only the parity of
![]() $r$
matters), then we have the corresponding local system on the Borel construction
$r$
matters), then we have the corresponding local system on the Borel construction
![]() $X_G$
, still denoted by
$X_G$
, still denoted by
![]() $\mathcal {F}$
. We define
$\mathcal {F}$
. We define
![]() $H^*_G(X, \mathcal {F})$
to be the local cohomology
$H^*_G(X, \mathcal {F})$
to be the local cohomology
![]() $H^*(X_G, \mathcal {F})$
, and the Leray–Serre spectral sequence (2) generalizes to this setting. For example,
$H^*(X_G, \mathcal {F})$
, and the Leray–Serre spectral sequence (2) generalizes to this setting. For example,
Remark 2.1 (Algebraic setting). For an algebraic variety
![]() $X_0$
defined over
$X_0$
defined over
![]() $\mathbb {R}$
, and a torsion
$\mathbb {R}$
, and a torsion
![]() $G$
-module
$G$
-module
![]() $\mathcal {F}$
, viewed as an étale sheaf on
$\mathcal {F}$
, viewed as an étale sheaf on
![]() $\textrm {Spec}(\mathbb {R})$
, the equivariant cohomology
$\textrm {Spec}(\mathbb {R})$
, the equivariant cohomology
![]() $H^*_G(X_0(\mathbb {C}), \mathcal {F})$
discussed above is canonically identified with the étale cohomology
$H^*_G(X_0(\mathbb {C}), \mathcal {F})$
discussed above is canonically identified with the étale cohomology
![]() $H^*_{\mathrm {\acute {e}t}}(X_0, a^*\mathcal {F})$
, where
$H^*_{\mathrm {\acute {e}t}}(X_0, a^*\mathcal {F})$
, where
![]() $a^*\mathcal {F}$
denotes the pullback of the étale sheaf
$a^*\mathcal {F}$
denotes the pullback of the étale sheaf
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $X_0$
via the structural morphism
$X_0$
via the structural morphism
![]() $a\colon X_0\to \textrm {Spec}(\mathbb {R})$
(see [Reference ScheidererSch94, Corollary 15.3.1]). Under this identification, the Leray–Serre spectral sequence is identified with the Hochschild–Serre spectral sequence.
$a\colon X_0\to \textrm {Spec}(\mathbb {R})$
(see [Reference ScheidererSch94, Corollary 15.3.1]). Under this identification, the Leray–Serre spectral sequence is identified with the Hochschild–Serre spectral sequence.
We will use the following basic fact.
Lemma 2.2.
Let
![]() $X$
be a real variety with
$X$
be a real variety with
![]() $X(\mathbb {R})\neq \emptyset$
and
$X(\mathbb {R})\neq \emptyset$
and
![]() $F$
a
$F$
a
![]() $G$
-module (e.g.
$G$
-module (e.g.
![]() $\mathbb {F}_2$
,
$\mathbb {F}_2$
,
![]() $\mathbb {Z}$
, or
$\mathbb {Z}$
, or
![]() $\mathbb {Z}(1)$
). Then, for any
$\mathbb {Z}(1)$
). Then, for any
![]() $i$
, the following pull-back map along the projection
$i$
, the following pull-back map along the projection
![]() $\pi \colon X_G\to BG$
is injective:
$\pi \colon X_G\to BG$
is injective:
Proof.
We can choose a real point
![]() $x\in X(\mathbb {R})$
, which induces a section
$x\in X(\mathbb {R})$
, which induces a section
![]() $s\colon BG\to X_G$
of
$s\colon BG\to X_G$
of
![]() $\pi$
. Therefore,
$\pi$
. Therefore,
![]() $s^*\circ \pi ^*=\textrm {id}$
and
$s^*\circ \pi ^*=\textrm {id}$
and
![]() $\pi ^*$
is injective.
$\pi ^*$
is injective.
2.2 Maximality
Recall that a real variety
![]() $(X, \sigma )$
is said to be maximal if the Smith–Thom inequality in Theorem1.1 becomes an equality:
$(X, \sigma )$
is said to be maximal if the Smith–Thom inequality in Theorem1.1 becomes an equality:
![]() $b_*(X, \mathbb {F}_2)=b_*(X(\mathbb {R}), \mathbb {F}_2)$
.
$b_*(X, \mathbb {F}_2)=b_*(X(\mathbb {R}), \mathbb {F}_2)$
.
We will use repeatedly the following result, which reformulates the maximality of a real variety
![]() $(X, \sigma )$
in terms of the surjectivity of the restriction map from equivariant cohomology to ordinary cohomology. A proof in a more general setting can be found, for instance, in [Reference tom DiecktD11, Chapter III, Proposition 4.16].
$(X, \sigma )$
in terms of the surjectivity of the restriction map from equivariant cohomology to ordinary cohomology. A proof in a more general setting can be found, for instance, in [Reference tom DiecktD11, Chapter III, Proposition 4.16].
Proposition 2.3 (Maximality and equivariant formality). Let
![]() $(X, \sigma )$
be a real variety. The following conditions are equivalent:
$(X, \sigma )$
be a real variety. The following conditions are equivalent:
-
(i)
 $X$
is maximal;
$X$
is maximal;
-
(ii) the action of
 $G$
on
$G$
on
 $H^*(X, \mathbb {F}_2)$
is trivial and the Leray–Serre spectral sequence (2) degenerates at the
$H^*(X, \mathbb {F}_2)$
is trivial and the Leray–Serre spectral sequence (2) degenerates at the
 $E_2$
-page;
$E_2$
-page;
-
(iii) the restriction homomorphism
 $H^*_G(X, \mathbb {F}_2)\to H^*(X, \mathbb {F}_2)$
is surjective.
$H^*_G(X, \mathbb {F}_2)\to H^*(X, \mathbb {F}_2)$
is surjective.
The condition (iii) is called the equivariant formality for the action of
![]() $G$
on
$G$
on
![]() $X$
(with coefficients
$X$
(with coefficients
![]() $\mathbb {F}_2$
), see [Reference FranzFra18]. This notion will be extended to motives in Section 11.
$\mathbb {F}_2$
), see [Reference FranzFra18]. This notion will be extended to motives in Section 11.
We state the following simple fact for future reference.
Lemma 2.4.
Let
![]() $(X, \sigma )$
be a real variety and let
$(X, \sigma )$
be a real variety and let
![]() $i$
be a natural number. Assume that
$i$
be a natural number. Assume that
![]() $H^i(X, \mathbb {Z})$
and
$H^i(X, \mathbb {Z})$
and
![]() $H^{i+1}(X, \mathbb {Z})$
are both 2-torsion-free. If the action of
$H^{i+1}(X, \mathbb {Z})$
are both 2-torsion-free. If the action of
![]() $G$
on
$G$
on
![]() $H^i(X, \mathbb {F}_2)$
is trivial (e.g. when
$H^i(X, \mathbb {F}_2)$
is trivial (e.g. when
![]() $X$
is maximal), then we have
$X$
is maximal), then we have
where
![]() $H^i(X, \mathbb {Z}(1))^G$
denotes the
$H^i(X, \mathbb {Z}(1))^G$
denotes the
![]() $\sigma$
-anti-invariant part of
$\sigma$
-anti-invariant part of
![]() $H^i(X, \mathbb {Z})$
.
$H^i(X, \mathbb {Z})$
.
Proof.
By the 2-torsion freeness assumption,
![]() $H^i(X, \mathbb {Z})^G\cap H^i(X, \mathbb {Z}(1))^G=0$
and we have an exact sequence
$H^i(X, \mathbb {Z})^G\cap H^i(X, \mathbb {Z}(1))^G=0$
and we have an exact sequence
For any
![]() $\alpha \in H^i(X, \mathbb {Z})$
, since
$\alpha \in H^i(X, \mathbb {Z})$
, since
![]() $\sigma$
acts trivially on its image
$\sigma$
acts trivially on its image
![]() $\overline {\alpha }\in H^i(X, \mathbb {F}_2)$
by assumption, the above exact sequence implies that there exist unique elements
$\overline {\alpha }\in H^i(X, \mathbb {F}_2)$
by assumption, the above exact sequence implies that there exist unique elements
![]() $\alpha _1, \alpha _2\in H^i(X, \mathbb {Z})$
such that
$\alpha _1, \alpha _2\in H^i(X, \mathbb {Z})$
such that
![]() $\alpha +\sigma ^*(\alpha )=2\alpha _1$
and
$\alpha +\sigma ^*(\alpha )=2\alpha _1$
and
![]() $\alpha -\sigma ^*(\alpha )=2\alpha _2$
. Again by the 2-torsion freeness assumption, we have
$\alpha -\sigma ^*(\alpha )=2\alpha _2$
. Again by the 2-torsion freeness assumption, we have
![]() $\alpha _1\in H^i(X, \mathbb {Z})^G$
,
$\alpha _1\in H^i(X, \mathbb {Z})^G$
,
![]() $\alpha _2\in H^i(X, \mathbb {Z}(1))^G$
and
$\alpha _2\in H^i(X, \mathbb {Z}(1))^G$
and
![]() $\alpha =\alpha _1+\alpha _2$
. The direct sum decomposition is proved.
$\alpha =\alpha _1+\alpha _2$
. The direct sum decomposition is proved.
2.3 K-theory
For a topological space
![]() $X$
, Atiyah [Reference AtiyahAti67] introduced the topological (complex) K-theory, denoted by
$X$
, Atiyah [Reference AtiyahAti67] introduced the topological (complex) K-theory, denoted by
![]() $\textrm {KU}^*(X)$
in this paper.Footnote
2
One key property of the topological K-theory is the Bott periodicity, which states that
$\textrm {KU}^*(X)$
in this paper.Footnote
2
One key property of the topological K-theory is the Bott periodicity, which states that
![]() $\textrm {KU}^*(X)\simeq \textrm {KU}^{*+2}(X)$
. Specifically,
$\textrm {KU}^*(X)\simeq \textrm {KU}^{*+2}(X)$
. Specifically,
![]() $\textrm {KU}^0(X)$
is defined as the Grothendieck group of the category of
$\textrm {KU}^0(X)$
is defined as the Grothendieck group of the category of
![]() $\mathcal {C}^\infty$
complex vector bundles on
$\mathcal {C}^\infty$
complex vector bundles on
![]() $X$
. Chern classes can be defined on
$X$
. Chern classes can be defined on
![]() $\textrm {KU}^0(X)$
using standard axioms, which allows the construction of the Chern polynomial map:
$\textrm {KU}^0(X)$
using standard axioms, which allows the construction of the Chern polynomial map:
This map sends
![]() $[E]$
to
$[E]$
to
![]() $1+c_1(E)t+c_2(E)t^2+\cdots$
, where
$1+c_1(E)t+c_2(E)t^2+\cdots$
, where
![]() $[E]$
denotes the class of a complex vector bundle
$[E]$
denotes the class of a complex vector bundle
![]() $E$
.
$E$
.
Now, let
![]() $(X, \sigma )$
be a real variety. A Real vector bundle on
$(X, \sigma )$
be a real variety. A Real vector bundle on
![]() $X$
, in the sense of Atiyah [Reference AtiyahAti66], is a complexFootnote
3
vector bundle
$X$
, in the sense of Atiyah [Reference AtiyahAti66], is a complexFootnote
3
vector bundle
![]() $\pi \colon E\to X$
together with an involution
$\pi \colon E\to X$
together with an involution
![]() $\widetilde \sigma$
covering
$\widetilde \sigma$
covering
![]() $\sigma$
:
$\sigma$
:

such that the map
![]() $\widetilde \sigma$
on the fibers
$\widetilde \sigma$
on the fibers
![]() $E_x\to E_{\sigma (x)}$
is
$E_x\to E_{\sigma (x)}$
is
![]() $\mathbb {C}$
-anti-linear for any
$\mathbb {C}$
-anti-linear for any
![]() $x\in X$
.
$x\in X$
.
Remark 2.5. To avoid confusion, it is important to note that, just like in the complex case, a Real vector bundle
![]() $(E, \widetilde {\sigma })$
does not necessarily have a holomorphic structure, and as a manifold,
$(E, \widetilde {\sigma })$
does not necessarily have a holomorphic structure, and as a manifold,
![]() $E$
does not have a natural complex analytic structure. Therefore, it does not make sense to say that
$E$
does not have a natural complex analytic structure. Therefore, it does not make sense to say that
![]() $\widetilde {\sigma }$
is anti-holomorphic. However, in the holomorphic context, we can define a holomorphic real vector bundle (also known as
$\widetilde {\sigma }$
is anti-holomorphic. However, in the holomorphic context, we can define a holomorphic real vector bundle (also known as
![]() $\mathbb {R}$
-bundle) on a real variety
$\mathbb {R}$
-bundle) on a real variety
![]() $(X, \sigma )$
. This is a holomorphic vector bundle
$(X, \sigma )$
. This is a holomorphic vector bundle
![]() $E\to X$
together with a real structure (an anti-holomorphic involution)
$E\to X$
together with a real structure (an anti-holomorphic involution)
![]() $\widetilde \sigma$
on
$\widetilde \sigma$
on
![]() $E$
, which covers
$E$
, which covers
![]() $\sigma$
and induces a
$\sigma$
and induces a
![]() $\mathbb {C}$
-anti-linear map
$\mathbb {C}$
-anti-linear map
![]() $E_x\to E_{\sigma (x)}$
for any
$E_x\to E_{\sigma (x)}$
for any
![]() $x\in X$
. According to GAGA, for a smooth projective
$x\in X$
. According to GAGA, for a smooth projective
![]() $\mathbb {R}$
-variety with a corresponding real form
$\mathbb {R}$
-variety with a corresponding real form
![]() $X_{\mathbb {R}}$
, the datum of a holomorphic real vector bundle on
$X_{\mathbb {R}}$
, the datum of a holomorphic real vector bundle on
![]() $X_{\mathbb {C}}$
is equivalent to that of an algebraic vector bundle on
$X_{\mathbb {C}}$
is equivalent to that of an algebraic vector bundle on
![]() $X_{\mathbb {R}}$
.
$X_{\mathbb {R}}$
.
Atiyah [Reference AtiyahAti66] defined the
![]() $\textrm {KR}$
-theory for a real variety
$\textrm {KR}$
-theory for a real variety
![]() $(X, \sigma )$
, denoted by
$(X, \sigma )$
, denoted by
![]() $\textrm {KR}^*(X)$
, which is a graded commutative ring, with unit given by the class of the trivial line bundle
$\textrm {KR}^*(X)$
, which is a graded commutative ring, with unit given by the class of the trivial line bundle
![]() $\mathbb {C}\times X$
with the complex conjugation on fibers. Specifically,
$\mathbb {C}\times X$
with the complex conjugation on fibers. Specifically,
![]() $\textrm {KR}^0(X)$
is the Grothendieck ring of the tensor category of Real vector bundles on
$\textrm {KR}^0(X)$
is the Grothendieck ring of the tensor category of Real vector bundles on
![]() $X$
. The
$X$
. The
![]() $\textrm {KR}$
-theory
$\textrm {KR}$
-theory
![]() $\textrm {KR}^*(X)$
satisfies Bott periodicity
$\textrm {KR}^*(X)$
satisfies Bott periodicity
![]() $\textrm {KR}^*(X)\simeq \textrm {KR}^{*+8}(X)$
and interpolates between the (complex) topological K-theory, the equivariant K-theory and the
$\textrm {KR}^*(X)\simeq \textrm {KR}^{*+8}(X)$
and interpolates between the (complex) topological K-theory, the equivariant K-theory and the
![]() $\operatorname {KO}$
-theory. More details on
$\operatorname {KO}$
-theory. More details on
![]() $\textrm {KR}$
-theory can be found in the original source [Reference AtiyahAti66].
$\textrm {KR}$
-theory can be found in the original source [Reference AtiyahAti66].
Forgetting the involution on the bundle gives a natural map from the
![]() $\textrm {KR}$
-theory to the topological K-theory:
$\textrm {KR}$
-theory to the topological K-theory:
2.4 Chern class
For a Real vector bundle
![]() $E$
on a real variety
$E$
on a real variety
![]() $X$
and a positive integer
$X$
and a positive integer
![]() $r\in \mathbb {N}$
, the
$r\in \mathbb {N}$
, the
![]() $r$
th equivariant Chern class of
$r$
th equivariant Chern class of
![]() $E$
, denoted by
$E$
, denoted by
![]() $c^G_r(E)$
, is defined by Kahn [Reference KahnKah87]. It is an element in
$c^G_r(E)$
, is defined by Kahn [Reference KahnKah87]. It is an element in
![]() $H^{2r}_G(X, \mathbb {Z}(r))$
, where
$H^{2r}_G(X, \mathbb {Z}(r))$
, where
![]() $\mathbb {Z}(r)=(\sqrt {-1})^r\mathbb {Z}$
is the Tate twist. We can define the equivariant Chern polynomial
$\mathbb {Z}(r)=(\sqrt {-1})^r\mathbb {Z}$
is the Tate twist. We can define the equivariant Chern polynomial
It is easy to see that equivariant Chern classes satisfy the same axioms as Chern classes. In particular, the additivity with respect to short exact sequences ensures that equivariant Chern classes are well-defined on
![]() $\textrm {KR}^0(X)$
. For our purpose, we are mostly interested in cohomology with
$\textrm {KR}^0(X)$
. For our purpose, we are mostly interested in cohomology with
![]() $\mathbb {F}_2$
-coefficients. We often view
$\mathbb {F}_2$
-coefficients. We often view
![]() $c_r^G(E)$
as an element in
$c_r^G(E)$
as an element in
![]() $H^{2r}_G(X, \mathbb {F}_2)$
, by composing with the natural map
$H^{2r}_G(X, \mathbb {F}_2)$
, by composing with the natural map
![]() $H^{2r}_G(X, \mathbb {Z}(r))\to H^{2r}_G(X, \mathbb {F}_2)$
. (Note that the Tate twists are dropped when passing to
$H^{2r}_G(X, \mathbb {Z}(r))\to H^{2r}_G(X, \mathbb {F}_2)$
. (Note that the Tate twists are dropped when passing to
![]() $\mathbb {F}_2$
-coefficients since the
$\mathbb {F}_2$
-coefficients since the
![]() $G$
-module
$G$
-module
![]() $\mathbb {F}_2(r)$
is always isomorphic to the trivial one
$\mathbb {F}_2(r)$
is always isomorphic to the trivial one
![]() $\mathbb {F}_2$
.)
$\mathbb {F}_2$
.)
We have the following commutative diagram:

where the top horizontal arrow is induced by forgetting the involution, and the middle and bottom horizontal arrows are restriction maps.
On the level of cohomology, there is a natural map of ‘restricting to the real locus’, which was introduced by Krasnov [Reference KrasnovKra94] and van Hamel [Reference van HamelvH00]:
For a Real vector bundle
![]() $E$
, we define
$E$
, we define
![]() $c_r^R(E)\in H^{r}(X(\mathbb {R}), \mathbb {F}_2)$
to be the image of the equivariant Chern class
$c_r^R(E)\in H^{r}(X(\mathbb {R}), \mathbb {F}_2)$
to be the image of the equivariant Chern class
![]() $c_r^G(E)\in H^{2r}_G(X, \mathbb {F}_2)$
under the above map; this element, called the
$c_r^G(E)\in H^{2r}_G(X, \mathbb {F}_2)$
under the above map; this element, called the
![]() $r$
th real Chern class of
$r$
th real Chern class of
![]() $E$
, is nothing but the
$E$
, is nothing but the
![]() $r$
th Stiefel–Whitney class of the bundle
$r$
th Stiefel–Whitney class of the bundle
![]() $E(\mathbb {R})$
on
$E(\mathbb {R})$
on
![]() $X(\mathbb {R})$
by Kahn [Reference KahnKah87, Théorème 4]. In the algebraic setting, for an algebraic vector bundle
$X(\mathbb {R})$
by Kahn [Reference KahnKah87, Théorème 4]. In the algebraic setting, for an algebraic vector bundle
![]() $E$
on a real variety
$E$
on a real variety
![]() $X_{\mathbb {R}}$
, we can equivalently define
$X_{\mathbb {R}}$
, we can equivalently define
![]() $c_r^R(E)$
as the image of the Chow-theoretic Chern class
$c_r^R(E)$
as the image of the Chow-theoretic Chern class
![]() $c_r(E)\in \textrm {CH}^r(X_{\mathbb {R}})$
under the Borel–Haefliger cycle class map [Reference Borel and HaefligerBH61]
$c_r(E)\in \textrm {CH}^r(X_{\mathbb {R}})$
under the Borel–Haefliger cycle class map [Reference Borel and HaefligerBH61]
![]() $\textrm {cl}_R\colon \textrm {CH}^r(X_{\mathbb {R}})\to H^r(X(\mathbb {R}), \mathbb {F}_2)$
.
$\textrm {cl}_R\colon \textrm {CH}^r(X_{\mathbb {R}})\to H^r(X(\mathbb {R}), \mathbb {F}_2)$
.
3. Basic operations preserving maximality
To facilitate easy reference, this section summarizes various operations that enable the construction of new maximal real varieties from existing ones.
3.1 Product
Lemma 3.1.
Let
![]() $X_1, \dots, X_n$
be real varieties. Then the product
$X_1, \dots, X_n$
be real varieties. Then the product
![]() $X:=X_1\times \dots \times X_n$
(endowed with the product real structure) is maximal if and only if each
$X:=X_1\times \dots \times X_n$
(endowed with the product real structure) is maximal if and only if each
![]() $X_i$
is maximal.
$X_i$
is maximal.
Proof.
By the Künneth formula
![]() $H^*(X, \mathbb {F}_2)\simeq \bigotimes _i H^*(X_i, \mathbb {F}_2)$
, we have
$H^*(X, \mathbb {F}_2)\simeq \bigotimes _i H^*(X_i, \mathbb {F}_2)$
, we have
Since
![]() $X(\mathbb {R})=X_1(\mathbb {R})\times \cdots \times X_n(\mathbb {R})$
, the Künneth formula yields that
$X(\mathbb {R})=X_1(\mathbb {R})\times \cdots \times X_n(\mathbb {R})$
, the Künneth formula yields that
Comparing (7) and (8), we see immediately that the maximality of all
![]() $X_i$
implies the maximality of
$X_i$
implies the maximality of
![]() $X$
, and also the converse by combining with the Smith–Thom inequality (Theorem1.1).
$X$
, and also the converse by combining with the Smith–Thom inequality (Theorem1.1).
3.2 Symmetric power
For a positive integer
![]() $n$
, the
$n$
, the
![]() $n$
th symmetric power of a complex variety
$n$
th symmetric power of a complex variety
![]() $X$
, denoted by
$X$
, denoted by
![]() $X^{(n)}$
or
$X^{(n)}$
or
![]() $\textrm {Sym}^n(X)$
, is defined as the quotient of
$\textrm {Sym}^n(X)$
, is defined as the quotient of
![]() $X^n$
by the permutation action of the symmetric group
$X^n$
by the permutation action of the symmetric group
![]() $\mathfrak {S}_n$
. More generally, for any subgroup
$\mathfrak {S}_n$
. More generally, for any subgroup
![]() $\Gamma$
of
$\Gamma$
of
![]() $\mathfrak {S}_n$
, one can define the
$\mathfrak {S}_n$
, one can define the
![]() $\Gamma$
-product of
$\Gamma$
-product of
![]() $X$
, denoted by
$X$
, denoted by
![]() $X^\Gamma$
, as the quotient
$X^\Gamma$
, as the quotient
![]() $X^n/\Gamma$
. A real structure
$X^n/\Gamma$
. A real structure
![]() $\sigma$
on
$\sigma$
on
![]() $X$
induces a natural real structure
$X$
induces a natural real structure
![]() $\sigma ^{(n)}$
on
$\sigma ^{(n)}$
on
![]() $X^{(n)}$
by sending
$X^{(n)}$
by sending
![]() $\{x_1, \dots, x_n\}$
to
$\{x_1, \dots, x_n\}$
to
![]() $\{\sigma (x_1), \dots, \sigma (x_n)\}$
, and more generally also a real structure
$\{\sigma (x_1), \dots, \sigma (x_n)\}$
, and more generally also a real structure
![]() $\sigma ^\Gamma$
on
$\sigma ^\Gamma$
on
![]() $X^\Gamma$
.
$X^\Gamma$
.
Note that even when
![]() $X$
is smooth,
$X$
is smooth,
![]() $X^\Gamma$
can be singular (e.g.
$X^\Gamma$
can be singular (e.g.
![]() $X^{(n)}$
is singular when
$X^{(n)}$
is singular when
![]() $\dim (X)\geqslant 2$
and
$\dim (X)\geqslant 2$
and
![]() $n\geqslant 2$
), but the notion of real structures still makes sense. Moreover, the Smith–Thom inequality remains valid and we can speak of maximality.
$n\geqslant 2$
), but the notion of real structures still makes sense. Moreover, the Smith–Thom inequality remains valid and we can speak of maximality.
We record the following theorem of Franz [Reference FranzFra18], which generalizes an earlier work of Biswas and D’Mello on curves [Reference Biswas and D’MelloBD17].
Theorem 3.2.
If
![]() $(X, \sigma )$
is a maximal real variety, then, for any
$(X, \sigma )$
is a maximal real variety, then, for any
![]() $n\gt 0$
and any subgroup
$n\gt 0$
and any subgroup
![]() $\Gamma$
of
$\Gamma$
of
![]() $\mathfrak {S}_n$
, the
$\mathfrak {S}_n$
, the
![]() $\Gamma$
-product
$\Gamma$
-product
![]() $(X^\Gamma, \sigma ^\Gamma )$
is maximal. In particular, all the symmetric powers
$(X^\Gamma, \sigma ^\Gamma )$
is maximal. In particular, all the symmetric powers
![]() $(X^{(n)}, \sigma ^{(n)})$
are maximal.
$(X^{(n)}, \sigma ^{(n)})$
are maximal.
3.3 Projective bundle
Let
![]() $X$
be a complex manifold or a complex algebraic variety, and let
$X$
be a complex manifold or a complex algebraic variety, and let
![]() $E$
be a holomorphic vector bundle of rank
$E$
be a holomorphic vector bundle of rank
![]() $r+1$
on
$r+1$
on
![]() $X$
. The relative projectivization gives rise to a complex manifold
$X$
. The relative projectivization gives rise to a complex manifold
![]() $\mathbb {P}(E):=\mathbb {P}_X(E)$
which is a
$\mathbb {P}(E):=\mathbb {P}_X(E)$
which is a
![]() $\mathbb {C}\mathbb {P}^r$
-bundle over
$\mathbb {C}\mathbb {P}^r$
-bundle over
![]() $X$
,
$X$
,
called the projective bundle associated to
![]() $E$
. If, moreover,
$E$
. If, moreover,
![]() $(X, \sigma )$
is a real variety and
$(X, \sigma )$
is a real variety and
![]() $(E, \widetilde {\sigma })$
is a holomorphic real vector bundle (i.e. an
$(E, \widetilde {\sigma })$
is a holomorphic real vector bundle (i.e. an
![]() $\mathbb {R}$
-bundle) on it (Remark 2.5), then
$\mathbb {R}$
-bundle) on it (Remark 2.5), then
![]() $\mathbb {P}(E)$
inherits a natural real structure, sending
$\mathbb {P}(E)$
inherits a natural real structure, sending
![]() $(x, [v])$
to
$(x, [v])$
to
![]() $(\sigma (x), [\widetilde \sigma (v)])$
, which makes
$(\sigma (x), [\widetilde \sigma (v)])$
, which makes
![]() $\pi$
a morphism of real varieties. (In the algebraic setting, it follows from the simple observation that the projective bundle construction is defined over the base field.)
$\pi$
a morphism of real varieties. (In the algebraic setting, it follows from the simple observation that the projective bundle construction is defined over the base field.)
Proposition 3.3.
Let
![]() $E$
be a holomorphic real vector bundle on a real variety
$E$
be a holomorphic real vector bundle on a real variety
![]() $X$
. Then
$X$
. Then
![]() $X$
is maximal if and only if the projective bundle
$X$
is maximal if and only if the projective bundle
![]() $\mathbb {P}(E)$
is maximal.
$\mathbb {P}(E)$
is maximal.
Proof.
Let
![]() $\mathcal {O}_{\pi }(1)$
be the relative Serre bundle. Denote by
$\mathcal {O}_{\pi }(1)$
be the relative Serre bundle. Denote by
![]() $\xi :=c_1^G(\mathcal {O}_\pi (1))\in H^2_G(\mathbb {P}(E), \mathbb {F}_2)$
its first equivariant Chern class as well as its image, the usual first Chern class, in
$\xi :=c_1^G(\mathcal {O}_\pi (1))\in H^2_G(\mathbb {P}(E), \mathbb {F}_2)$
its first equivariant Chern class as well as its image, the usual first Chern class, in
![]() $H^2(\mathbb {P}(E), \mathbb {F}_2)$
, and denote by
$H^2(\mathbb {P}(E), \mathbb {F}_2)$
, and denote by
![]() $\xi _R:=c_1^R(\mathcal {O}_\pi (1))\in H^1(\mathbb {P}(E)(\mathbb {R}), \mathbb {F}_2)$
its first real Chern class (see Section 2.4).
$\xi _R:=c_1^R(\mathcal {O}_\pi (1))\in H^1(\mathbb {P}(E)(\mathbb {R}), \mathbb {F}_2)$
its first real Chern class (see Section 2.4).
Let
![]() $r+1$
be the rank of
$r+1$
be the rank of
![]() $E$
. By definition, the restriction of
$E$
. By definition, the restriction of
![]() $\xi$
to a fiber
$\xi$
to a fiber
![]() $\mathbb {C}\mathbb {P}^r$
is a generator of its cohomology ring
$\mathbb {C}\mathbb {P}^r$
is a generator of its cohomology ring
![]() $H^*(\mathbb {C}\mathbb {P}^r, \mathbb {F}_2)=\mathbb {F}_2[\xi ]/(\xi ^{r+1})$
. By the Leray–Hirsch theorem,
$H^*(\mathbb {C}\mathbb {P}^r, \mathbb {F}_2)=\mathbb {F}_2[\xi ]/(\xi ^{r+1})$
. By the Leray–Hirsch theorem,
In particular,
On the other hand, it is clear that the real locus
![]() $\mathbb {P}(E)(\mathbb {R})$
is a
$\mathbb {P}(E)(\mathbb {R})$
is a
![]() $\mathbb {R}\mathbb {P}^r$
-bundle over
$\mathbb {R}\mathbb {P}^r$
-bundle over
![]() $X(\mathbb {R})$
. Again, by construction, the restriction of
$X(\mathbb {R})$
. Again, by construction, the restriction of
![]() $\xi _R$
to a fiber is a generator of the cohomology ring
$\xi _R$
to a fiber is a generator of the cohomology ring
![]() $H^*(\mathbb {R}\mathbb {P}^r, \mathbb {F}_2)=\mathbb {F}_2[\xi _R]/(\xi _R^{r+1})$
. By the Leray–Hirsch theorem,
$H^*(\mathbb {R}\mathbb {P}^r, \mathbb {F}_2)=\mathbb {F}_2[\xi _R]/(\xi _R^{r+1})$
. By the Leray–Hirsch theorem,
Consequently,
Comparing (10) and (12), we see that
![]() $X$
is maximal if and only if
$X$
is maximal if and only if
![]() $\mathbb {P}(E)$
is maximal.
$\mathbb {P}(E)$
is maximal.
Remark 3.4. Proposition 3.3 can be easily generalized to flag bundles (e.g. Grassmannian bundles) associated to a holomorphic real vector bundle. The argument is similar: in the above proof, one replaces the usual (respectively, equivariant, real) first Chern class of the relative Serre bundle by the usual (respectively, equivariant, real) Chern classes of the universal/tautological bundles, and apply Leray–Hirsch in the same way. A more conceptual proof is via motives (see Section 11.4). In general, it is an interesting question to relate the maximality of the total space of a fibration to the maximalities of the base and the fiber.
3.4 Blow-up
Let
![]() $X$
be a smooth real variety and let
$X$
be a smooth real variety and let
![]() $Y$
be a smooth real subvariety of codimension
$Y$
be a smooth real subvariety of codimension
![]() $c\geqslant 2$
. Then the blow-up
$c\geqslant 2$
. Then the blow-up
![]() $\textrm {Bl}_YX$
, as well as the exceptional divisor
$\textrm {Bl}_YX$
, as well as the exceptional divisor
![]() $E\cong \mathbb {P}(N_{Y/X})$
, has a natural real structure, where
$E\cong \mathbb {P}(N_{Y/X})$
, has a natural real structure, where
![]() $N_{Y/X}$
is the normal bundle. We have the commutative diagram of morphisms of real varieties.
$N_{Y/X}$
is the normal bundle. We have the commutative diagram of morphisms of real varieties.

Proposition 3.5.
If
![]() $X$
and
$X$
and
![]() $Y$
are both maximal, then
$Y$
are both maximal, then
![]() $\textrm {Bl}_YX$
is maximal.
$\textrm {Bl}_YX$
is maximal.
Proof.
We have the following commutative diagram (the coefficients
![]() $\mathbb {F}_2$
are omitted):
$\mathbb {F}_2$
are omitted):

where all the vertical arrows are restriction maps, and both horizontal maps are given by
 \begin{align*}(\alpha, \beta _1, \dots, \beta _{c-1})\mapsto \tau ^*(\alpha )+\sum _{k=1}^{c-1} j_*(p^*(\beta _k)\smile \xi ^{k-1}),\end{align*}
\begin{align*}(\alpha, \beta _1, \dots, \beta _{c-1})\mapsto \tau ^*(\alpha )+\sum _{k=1}^{c-1} j_*(p^*(\beta _k)\smile \xi ^{k-1}),\end{align*}
where
![]() $\xi$
is
$\xi$
is
![]() $c^G_1(\mathcal {O}_{p}(1))\in H^2_G(E)$
in the top row and is
$c^G_1(\mathcal {O}_{p}(1))\in H^2_G(E)$
in the top row and is
![]() $c_1(\mathcal {O}_{p}(1))\in H^2(E)$
in the bottom row; the commutativity of the diagram follows from the fact that all maps in (13) are real maps and
$c_1(\mathcal {O}_{p}(1))\in H^2(E)$
in the bottom row; the commutativity of the diagram follows from the fact that all maps in (13) are real maps and
![]() $\mathcal {O}_p(1)$
is an
$\mathcal {O}_p(1)$
is an
![]() $\mathbb {R}$
-line bundle on
$\mathbb {R}$
-line bundle on
![]() $E$
.
$E$
.
Now in diagram (14), the bottom arrow is an isomorphism by the blow-up formula,Footnote
4
and the left vertical arrow is surjective by the maximalities of
![]() $X$
and
$X$
and
![]() $Y$
(Proposition 2.3). Therefore, the right vertical arrow is surjective. By Proposition 2.3,
$Y$
(Proposition 2.3). Therefore, the right vertical arrow is surjective. By Proposition 2.3,
![]() $\textrm {Bl}_YX$
is maximal.
$\textrm {Bl}_YX$
is maximal.
Remark 3.6 (Flips and flops). There are other types of basic birational transformations that preserve maximality. For instance, a standard flipFootnote 5 (or flop) of a maximal real variety along a maximal real flipping/flopping center is again maximal (this can be deduced from the blow-up formula, or by using Jiang [Reference JiangJia21, Corollary 3.8]). Similarly, the Mukai flop of a maximal real hyper-Kähler manifold along a real flopping center is maximal (use, e.g., [Reference Fu, Hoskins and LehalleurFHPL23, Theorem 3.6]).
We give an example of application. Given a smooth compact complex manifold
![]() $X$
and an integer
$X$
and an integer
![]() $n$
, the configuration space
$n$
, the configuration space
![]() $F(X, n)$
is the open subset of
$F(X, n)$
is the open subset of
![]() $X^n$
parameterizing
$X^n$
parameterizing
![]() $n$
ordered distinct points in
$n$
ordered distinct points in
![]() $X$
. Fulton and MacPherson constructed in [Reference Fulton and MacPhersonFM94] a compactification
$X$
. Fulton and MacPherson constructed in [Reference Fulton and MacPhersonFM94] a compactification
![]() $X[n]$
of
$X[n]$
of
![]() $F(X, n)$
, such that the complement is a simple normal crossing divisor with geometric description. The quickest way to define
$F(X, n)$
, such that the complement is a simple normal crossing divisor with geometric description. The quickest way to define
![]() $X[n]$
is as the closure of the embedding
$X[n]$
is as the closure of the embedding
![]() $F(X,n)\subset X^n\times \prod _{I} \textrm {Bl}_{\delta }(X^I)$
, where
$F(X,n)\subset X^n\times \prod _{I} \textrm {Bl}_{\delta }(X^I)$
, where
![]() $I$
runs through all subsets of
$I$
runs through all subsets of
![]() $\{1, \cdots, n\}$
with
$\{1, \cdots, n\}$
with
![]() $|I|\geqslant 2$
,
$|I|\geqslant 2$
,
![]() $X^I$
is the
$X^I$
is the
![]() $|I|$
-the power of
$|I|$
-the power of
![]() $X$
, and
$X$
, and
![]() $\delta$
is the small(est) diagonal of
$\delta$
is the small(est) diagonal of
![]() $X^I$
. Clearly, a real structure on
$X^I$
. Clearly, a real structure on
![]() $X$
induces a real structure on
$X$
induces a real structure on
![]() $X[n]$
.
$X[n]$
.
Proposition 3.7.
If
![]() $X$
is a maximal real variety, then
$X$
is a maximal real variety, then
![]() $X[n]$
, equipped with the induced real structure, is also maximal.
$X[n]$
, equipped with the induced real structure, is also maximal.
Proof.
We use the geometric inductive construction of Fulton–MacPherson’s compactification. We refer the reader to [Reference Fulton and MacPhersonFM94, §3] for the details. Roughly speaking, starting from
![]() $X^n$
,
$X^n$
,
![]() $X[n]$
is obtained as a sequence of
$X[n]$
is obtained as a sequence of
![]() $ 2^n-n-1$
blow-ups along centers that are themselves successive blow-ups of similar form. By repeatedly using Proposition 3.5, one shows by induction that all the varieties obtained as well as the blow-up centers are maximal.
$ 2^n-n-1$
blow-ups along centers that are themselves successive blow-ups of similar form. By repeatedly using Proposition 3.5, one shows by induction that all the varieties obtained as well as the blow-up centers are maximal.
3.5 Generically finite surjection of odd degree
Proposition 3.8.
Let
![]() $f\colon X\to Y$
be a surjective proper real morphism between smooth real varieties. Assume that
$f\colon X\to Y$
be a surjective proper real morphism between smooth real varieties. Assume that
![]() $f$
admits a rational multi-section of odd degree; for example, when
$f$
admits a rational multi-section of odd degree; for example, when
![]() $f$
is generically finite of odd degree. If
$f$
is generically finite of odd degree. If
![]() $X$
is maximal, then
$X$
is maximal, then
![]() $Y$
is maximal.
$Y$
is maximal.
Proof. We have the commutative diagram

where the horizontal arrows are push-forwards and the vertical arrows are restriction maps. We claim that the bottom map is surjective. Indeed, let
![]() $S$
be the closure of a rational multi-section of odd degree, then by projection formula we have that
$S$
be the closure of a rational multi-section of odd degree, then by projection formula we have that
![]() $f_*(f^*(-)\smile [S])=\deg (S/Y)\cdot \textrm {id}$
, which is the identity since
$f_*(f^*(-)\smile [S])=\deg (S/Y)\cdot \textrm {id}$
, which is the identity since
![]() $\deg (S/Y)$
is odd and we are working with
$\deg (S/Y)$
is odd and we are working with
![]() $\mathbb {F}_2$
-coefficients. Therefore,
$\mathbb {F}_2$
-coefficients. Therefore,
![]() $f_*$
is surjective. The left vertical map is surjective by the maximality of
$f_*$
is surjective. The left vertical map is surjective by the maximality of
![]() $X$
. Therefore, the right vertical arrow is also surjective. By Proposition 2.3, it yields that
$X$
. Therefore, the right vertical arrow is also surjective. By Proposition 2.3, it yields that
![]() $Y$
is maximal.
$Y$
is maximal.
Remark 3.9. The statement does not hold for maps of even degree. As a counter-example, take a maximal real surface
![]() $S$
with non-maximal Hilbert square
$S$
with non-maximal Hilbert square
![]() $S^{[2]}$
(such surface exists by [Reference Kharlamov and RăsdeaconuKR23], see Remark 7.4), then the degree-2 quotient map
$S^{[2]}$
(such surface exists by [Reference Kharlamov and RăsdeaconuKR23], see Remark 7.4), then the degree-2 quotient map
![]() $\textrm {Bl}_{\Delta }(S\times S)\to S^{[2]}$
is from a maximal variety to a non-maximal one.
$\textrm {Bl}_{\Delta }(S\times S)\to S^{[2]}$
is from a maximal variety to a non-maximal one.
3.6 Albanese and Picard
Recall that for a projective complex manifold
![]() $X$
, there are two naturally associated abelian varieties, namely, its Picard variety
$X$
, there are two naturally associated abelian varieties, namely, its Picard variety
and its Albanese variety
A real structure on
![]() $X$
naturally induces real structures on
$X$
naturally induces real structures on
![]() $\textrm {Alb}(X)$
and
$\textrm {Alb}(X)$
and
![]() $\textrm {Pic}^0(X)$
(see [Reference Ciliberto and PedriniCP96, §2.7]), they are moreover proper in the sense of [Reference Ciliberto and PedriniCP96]. The theory of real abelian varieties was developed by Comessatti [Reference ComessattiCom24, Reference ComessattiCom25] ; see also [Reference Ciliberto and PedriniCP96] for a recent account.
$\textrm {Pic}^0(X)$
(see [Reference Ciliberto and PedriniCP96, §2.7]), they are moreover proper in the sense of [Reference Ciliberto and PedriniCP96]. The theory of real abelian varieties was developed by Comessatti [Reference ComessattiCom24, Reference ComessattiCom25] ; see also [Reference Ciliberto and PedriniCP96] for a recent account.
Proposition 3.10.
Let
![]() $X$
be a smooth projective real variety with
$X$
be a smooth projective real variety with
![]() $H_1(X, \mathbb {Z})$
torsion-free. If
$H_1(X, \mathbb {Z})$
torsion-free. If
![]() $X$
is maximal, then
$X$
is maximal, then
![]() $\textrm {Alb}(X)$
and
$\textrm {Alb}(X)$
and
![]() $\textrm {Pic}^0(X)$
are also maximal. In particular, the dual of a maximal real abelian variety is again maximal.
$\textrm {Pic}^0(X)$
are also maximal. In particular, the dual of a maximal real abelian variety is again maximal.
Proof.
Recall that
![]() $\textrm {Alb}(X)$
and
$\textrm {Alb}(X)$
and
![]() $\textrm {Pic}^0(X)$
are both of dimension
$\textrm {Pic}^0(X)$
are both of dimension
![]() $q:=h^{1,0}(X)$
, the irregularity of
$q:=h^{1,0}(X)$
, the irregularity of
![]() $X$
, and they both have total
$X$
, and they both have total
![]() $\mathbb {F}_2$
-Betti number
$\mathbb {F}_2$
-Betti number
![]() $2^{2q}$
. Denote by
$2^{2q}$
. Denote by
![]() $\sigma$
the real structure on
$\sigma$
the real structure on
![]() $X$
. Recall that the first Comessatti characteristic is
$X$
. Recall that the first Comessatti characteristic is
The maximality of
![]() $X$
implies that
$X$
implies that
![]() $\sigma$
acts trivially on
$\sigma$
acts trivially on
![]() $H^1(X, \mathbb {F}_2)$
, hence
$H^1(X, \mathbb {F}_2)$
, hence
![]() $\lambda _1(X)=0$
.
$\lambda _1(X)=0$
.
We apply [Reference Ciliberto and PedriniCP96, Theorem 2.7.2 and Theorem 2.7.9], which say that
![]() $\textrm {Alb}(X)(\mathbb {R})$
and
$\textrm {Alb}(X)(\mathbb {R})$
and
![]() $\textrm {Pic}^0(X)(\mathbb {R})$
are both isomorphic as Lie groups to
$\textrm {Pic}^0(X)(\mathbb {R})$
are both isomorphic as Lie groups to
![]() $(\mathbb {R}/\mathbb {Z})^q\times (\mathbb {Z}/2)^{q-\lambda _1}$
. Since
$(\mathbb {R}/\mathbb {Z})^q\times (\mathbb {Z}/2)^{q-\lambda _1}$
. Since
![]() $\lambda _1=0$
, the total
$\lambda _1=0$
, the total
![]() $\mathbb {F}_2$
-Betti number is clearly
$\mathbb {F}_2$
-Betti number is clearly
![]() $2^{2q}$
, hence
$2^{2q}$
, hence
![]() $\textrm {Alb}(X)$
and
$\textrm {Alb}(X)$
and
![]() $\textrm {Pic}^0(X)$
are maximal. The assertion for dual abelian varieties follows since
$\textrm {Pic}^0(X)$
are maximal. The assertion for dual abelian varieties follows since
![]() $\widehat {A}\cong \textrm {Pic}^0(A)$
, as real varieties.
$\widehat {A}\cong \textrm {Pic}^0(A)$
, as real varieties.
Remark 3.11 (Dual complex tori). In fact, the same argument shows that if a complex torus
![]() $T$
equipped with a real structure is maximal, then its dual torus
$T$
equipped with a real structure is maximal, then its dual torus
![]() $\widehat {T}$
, equipped with the natural real structure, is also maximal.
$\widehat {T}$
, equipped with the natural real structure, is also maximal.
The following result was first obtained by Gross and Harris [Reference Gross and HarrisGH81].
Corollary 3.12 (Jacobian). Let
![]() $C$
be a smooth projective real curve. If
$C$
be a smooth projective real curve. If
![]() $C$
is maximal, then its Jacobian
$C$
is maximal, then its Jacobian
![]() $J(C)$
is also maximal. Conversely, if
$J(C)$
is also maximal. Conversely, if
![]() $J(C)$
is maximal and
$J(C)$
is maximal and
![]() $C(\mathbb {R})\neq \emptyset$
, then
$C(\mathbb {R})\neq \emptyset$
, then
![]() $C$
is also maximal.
$C$
is also maximal.
Proof.
The first claim is a special case of Proposition 3.10, since the Jacobian of
![]() $C$
is identified with
$C$
is identified with
![]() $\textrm {Alb}(C)$
(and also with
$\textrm {Alb}(C)$
(and also with
![]() $\textrm {Pic}^0(C)$
by the Abel–Jacobi theorem). Conversely, the Abel–Jacobi map
$\textrm {Pic}^0(C)$
by the Abel–Jacobi theorem). Conversely, the Abel–Jacobi map
![]() $a: C\to J(C)$
, which is a real morphism, induces an isomorphism
$a: C\to J(C)$
, which is a real morphism, induces an isomorphism
![]() $a^*\colon H^1(J(C), \mathbb {F}_2)\xrightarrow {\cong } H^1(C, \mathbb {F}_2)$
. In the commutative diagram
$a^*\colon H^1(J(C), \mathbb {F}_2)\xrightarrow {\cong } H^1(C, \mathbb {F}_2)$
. In the commutative diagram

the left vertical map is surjective and the bottom map is an isomorphism. Therefore, the right vertical map is surjective.
![]() $H^j_G(C, \mathbb {F}_2)\to H^j(C, \mathbb {F}_2)$
is clearly surjective for
$H^j_G(C, \mathbb {F}_2)\to H^j(C, \mathbb {F}_2)$
is clearly surjective for
![]() $j=0$
and also for
$j=0$
and also for
![]() $j=2$
as
$j=2$
as
![]() $C(\mathbb {R})\neq \emptyset$
. Hence
$C(\mathbb {R})\neq \emptyset$
. Hence
![]() $C$
is maximal by Proposition 2.3.
$C$
is maximal by Proposition 2.3.
Remark 3.13. Corollary 3.12 can also be deduced from Franz’s Theorem 3.2: for
![]() $N\geqslant 2g+2$
, the symmetric power
$N\geqslant 2g+2$
, the symmetric power
![]() $C^{(N)}$
, which is maximal by Theorem 3.2, is a projective bundle over
$C^{(N)}$
, which is maximal by Theorem 3.2, is a projective bundle over
![]() $J^N(C)$
. By Proposition 3.3,
$J^N(C)$
. By Proposition 3.3,
![]() $J^{N}(C)$
is maximal. Since
$J^{N}(C)$
is maximal. Since
![]() $C(\mathbb {R})\neq \emptyset$
,
$C(\mathbb {R})\neq \emptyset$
,
![]() $J(C)$
is isomorphic to
$J(C)$
is isomorphic to
![]() $J^N(C)$
as real varieties, hence is maximal.
$J^N(C)$
as real varieties, hence is maximal.
3.7 Intermediate Jacobians
For a smooth projective variety
![]() $X$
of odd dimension
$X$
of odd dimension
![]() $n=2m+1$
with the only non-zero Hodge numbers
$n=2m+1$
with the only non-zero Hodge numbers
![]() $h^{i,i}(X)$
for all
$h^{i,i}(X)$
for all
![]() $0\leqslant i\leqslant n$
and
$0\leqslant i\leqslant n$
and
![]() $h^{m, m+1}=h^{m+1, m}$
. Its intermediate Jacobian, denoted by
$h^{m, m+1}=h^{m+1, m}$
. Its intermediate Jacobian, denoted by
![]() $J(X)$
, is a principally polarized abelian variety with the underlying complex torus
$J(X)$
, is a principally polarized abelian variety with the underlying complex torus
and with polarization induced by the intersection pairing on
![]() $H^n(X, \mathbb {Z})$
.
$H^n(X, \mathbb {Z})$
.
Examples of such varieties include cubic 3-folds, cubic 5-folds, quartic 3-folds, quartic double solids, complete intersections of two even-dimensional quadrics, complete intersections of three odd-dimensional quadrics, odd-dimensional Gushel–Mukai varieties, etc. A real structure
![]() $\sigma$
on
$\sigma$
on
![]() $X$
induces a
$X$
induces a
![]() $\mathbb {C}$
-anti-linear map
$\mathbb {C}$
-anti-linear map
![]() $H^{m, m+1}(X)\to H^{m+1, m}(X)=\overline {H^{m, m+1}(X)}$
respecting
$H^{m, m+1}(X)\to H^{m+1, m}(X)=\overline {H^{m, m+1}(X)}$
respecting
![]() $H^n(X, \mathbb {Z})_{\operatorname {tf}}$
, and thus a natural real structure on
$H^n(X, \mathbb {Z})_{\operatorname {tf}}$
, and thus a natural real structure on
![]() $J(X)$
. The following result for the Fano surface of lines is due to Krasnov [Reference KrasnovKra05].
$J(X)$
. The following result for the Fano surface of lines is due to Krasnov [Reference KrasnovKra05].
Proposition 3.14.
Let
![]() $X$
be a smooth real cubic 3-fold. If
$X$
be a smooth real cubic 3-fold. If
![]() $X$
is maximal, then its Fano surface of lines
$X$
is maximal, then its Fano surface of lines
![]() $F(X)$
and the intermediate Jacobian
$F(X)$
and the intermediate Jacobian
![]() $J(X)$
are also maximal.
$J(X)$
are also maximal.
Proof.
We recall the proof for convenience of readers. Let
![]() $\mathcal {P}:=\{(x, L)\in X\times F(X)\ |\ x\in L\}$
be the incidence variety, or equivalently, the universal projective line over
$\mathcal {P}:=\{(x, L)\in X\times F(X)\ |\ x\in L\}$
be the incidence variety, or equivalently, the universal projective line over
![]() $F(X)$
. The correspondence via
$F(X)$
. The correspondence via
![]() $\mathcal {P}$
induces an isomorphism ([Reference Clemens and GriffithsCG72]):
$\mathcal {P}$
induces an isomorphism ([Reference Clemens and GriffithsCG72]):
Consider the commutative diagram

where the top map is the correspondence induced by the equivariant cycle class
![]() $\textrm {cl}_G(\mathcal {P})$
, the bottom map is an isomorphism by (16) and the universal coefficient theorem, the vertical arrows are restriction maps and the left one is surjective by assumption. Therefore, the right arrow
$\textrm {cl}_G(\mathcal {P})$
, the bottom map is an isomorphism by (16) and the universal coefficient theorem, the vertical arrows are restriction maps and the left one is surjective by assumption. Therefore, the right arrow
![]() $H^1_G(F(X), \mathbb {F}_2)\to H^1(F(X), \mathbb {F}_2)$
is surjective too. Since
$H^1_G(F(X), \mathbb {F}_2)\to H^1(F(X), \mathbb {F}_2)$
is surjective too. Since
![]() $H^2(F(X), \mathbb {F}_2)=\wedge^2H^1(F(X)), \mathbb {F}_2)$
, we have that
$H^2(F(X), \mathbb {F}_2)=\wedge^2H^1(F(X)), \mathbb {F}_2)$
, we have that
![]() $H^*_G(F(X), \mathbb {F}_2)\to H^*(F(X), \mathbb {F}_2)$
is surjective, hence
$H^*_G(F(X), \mathbb {F}_2)\to H^*(F(X), \mathbb {F}_2)$
is surjective, hence
![]() $F(X)$
is maximal. Consequently, by Proposition 3.10,
$F(X)$
is maximal. Consequently, by Proposition 3.10,
![]() $\textrm {Alb}(F(X))$
is also maximal. Finally, by [Reference Clemens and GriffithsCG72], we have
$\textrm {Alb}(F(X))$
is also maximal. Finally, by [Reference Clemens and GriffithsCG72], we have
![]() $J(X)\cong \textrm {Alb}(F(X))$
and it is straightforward to check that the isomorphism is defined over
$J(X)\cong \textrm {Alb}(F(X))$
and it is straightforward to check that the isomorphism is defined over
![]() $\mathbb {R}$
. Therefore,
$\mathbb {R}$
. Therefore,
![]() $J(X)$
is also maximal.
$J(X)$
is also maximal.
The same argument shows similar results as follows:
-
– for a general real cubic 5-fold
 $X$
that is maximal, its Fano variety of planes
$X$
that is maximal, its Fano variety of planes
 $F_2(X)$
and its intermediate Jacobian
$F_2(X)$
and its intermediate Jacobian
 $J(X)$
are also maximal;
$J(X)$
are also maximal; -
– for a general real quartic 3-fold
 $X$
that is maximal, its Fano variety of conics
$X$
that is maximal, its Fano variety of conics
 $F_c(X)$
and its intermediate Jacobian
$F_c(X)$
and its intermediate Jacobian
 $J(X)$
are also maximal;
$J(X)$
are also maximal; -
– for a real smooth Gushel–Mukai 3-fold or 5-fold
 $X$
that is maximal, its double EPW surface
$X$
that is maximal, its double EPW surface
 $\widetilde {Y}^{\geqslant 2}_{A(X)}$
and its intermediate Jacobian
$\widetilde {Y}^{\geqslant 2}_{A(X)}$
and its intermediate Jacobian
 $J(X)$
are also maximal;
$J(X)$
are also maximal;
where in place of the results of Clemens and Griffiths [Reference Clemens and GriffithsCG72], one applies results of Collino [Reference CollinoCol86], Letizia [Reference LetiziaLet84] and Debarre–Kuznetsov [Reference Debarre and KuznetsovDK20], respectively.
4. Variants of maximality
Inspired by Proposition 2.3, we propose several variants of the notion of maximality for real varieties. As we will see, these notions are closely related to topological properties, for example maximality, of surfaces. Their implications for higher-dimensional varieties are not clear to the author.
Definition 4.1 (K-maximality). Let
![]() $X$
be a real variety. We say that
$X$
be a real variety. We say that
![]() $X$
is
$X$
is
![]() $K^0$
-maximal if the natural map forgetting the real structure
$K^0$
-maximal if the natural map forgetting the real structure
is surjective. Similarly, one can define
![]() $K^1$
-maximality by the surjectivity of
$K^1$
-maximality by the surjectivity of
![]() $\textrm {KR}^1(X)\to \textrm {KU}^1(X)$
.
$\textrm {KR}^1(X)\to \textrm {KU}^1(X)$
.
We say that
![]() $X$
is K-maximal if it is
$X$
is K-maximal if it is
![]() $K^0$
-maximal and
$K^0$
-maximal and
![]() $K^1$
-maximal.
$K^1$
-maximal.
Definition 4.2 (
![]() $c_1$
-maximality). Let
$c_1$
-maximality). Let
![]() $X$
be a real variety. We say that
$X$
be a real variety. We say that
![]() $X$
is
$X$
is
![]() $c_1$
-maximal if the first Chern class map
$c_1$
-maximal if the first Chern class map
is surjective. By first taking the determinant bundle, it is clear that the
![]() $c_1$
-maximality is equivalent to the surjectivity of
$c_1$
-maximality is equivalent to the surjectivity of
Thanks to [Reference KahnKah87, Proposition 1], this condition is also equivalent to the surjectivity of the following natural map:
It would be very interesting to compare these notions to the usual maximality. First, we have a few easy relations.
Lemma 4.3.
Let
![]() $X$
be a smooth projective real variety.
$X$
be a smooth projective real variety.
-
(i) If
 $X$
is
$X$
is
 $K^0$
-maximal
Footnote
6
and
$K^0$
-maximal
Footnote
6
and
 $H^3(X, \mathbb {Z})$
has no 2-torsion, then
$H^3(X, \mathbb {Z})$
has no 2-torsion, then
 $X$
is
$X$
is
 $c_1$
-maximal.
$c_1$
-maximal.
-
(ii) If
 $X$
is a
$X$
is a
 $c_1$
-maximal
$c_1$
-maximal
 $\mathbb {R}$
-surface such that
$\mathbb {R}$
-surface such that
 $X(\mathbb {R})\neq \emptyset$
and
$X(\mathbb {R})\neq \emptyset$
and
 $b_1(X)=0$
, then
$b_1(X)=0$
, then
 $X$
is maximal.
$X$
is maximal.
Proof.
For (i), the map
![]() $c_1\colon \textrm {KR}^0(X)\to H^2(X, \mathbb {F}_2)$
is the composition
$c_1\colon \textrm {KR}^0(X)\to H^2(X, \mathbb {F}_2)$
is the composition
The first map is surjective by assumption, the second map is surjective since
![]() $K(\mathbb {Z}, 2)\cong \mathbb {C}\mathbb {P}^{\infty }$
classifies vector bundles of rank 1 and the third map is surjective since
$K(\mathbb {Z}, 2)\cong \mathbb {C}\mathbb {P}^{\infty }$
classifies vector bundles of rank 1 and the third map is surjective since
![]() $H^3(X, \mathbb {Z})$
has no 2-torsion.
$H^3(X, \mathbb {Z})$
has no 2-torsion.
For (ii), since
![]() $c_1 \colon \textrm {KR}^0(X)\to H^2(X, \mathbb {F}_2)$
factors through the equivariant first Chern class map
$c_1 \colon \textrm {KR}^0(X)\to H^2(X, \mathbb {F}_2)$
factors through the equivariant first Chern class map
![]() $c_1^G \colon \textrm {KR}^0(X)\to H^2_G(X, \mathbb {F}_2)$
, we get that
$c_1^G \colon \textrm {KR}^0(X)\to H^2_G(X, \mathbb {F}_2)$
, we get that
![]() $H^2_G(X, \mathbb {F}_2)\to H^2(X, \mathbb {F}_2)$
is surjective. Since
$H^2_G(X, \mathbb {F}_2)\to H^2(X, \mathbb {F}_2)$
is surjective. Since
![]() $b_1(X)=0$
,
$b_1(X)=0$
,
![]() $H^j_G(X, \mathbb {F}_2)\to H^j(X, \mathbb {F}_2)$
is surjective for
$H^j_G(X, \mathbb {F}_2)\to H^j(X, \mathbb {F}_2)$
is surjective for
![]() $j=1, 3$
. Since
$j=1, 3$
. Since
![]() $X(\mathbb {R})\neq \emptyset$
,
$X(\mathbb {R})\neq \emptyset$
,
![]() $H^4_G(X, \mathbb {F}_2)\to H^4(X, \mathbb {F}_2)$
is also surjective. Therefore,
$H^4_G(X, \mathbb {F}_2)\to H^4(X, \mathbb {F}_2)$
is also surjective. Therefore,
![]() $X$
is maximal.
$X$
is maximal.
For maximal real surfaces, the
![]() $c_1$
-maximality can be reinterpreted geometrically as follows (the equivalence between (ii) and (iii) below is due to Kharlamov, who kindly taught me the nice geometric argument and allowed me to include it here).
$c_1$
-maximality can be reinterpreted geometrically as follows (the equivalence between (ii) and (iii) below is due to Kharlamov, who kindly taught me the nice geometric argument and allowed me to include it here).
Proposition 4.4.
Let
![]() $X$
be a maximal smooth projective real surface with
$X$
be a maximal smooth projective real surface with
![]() $H^1(X, \mathbb {F}_2)=0$
. Then the following conditions are equivalent:
$H^1(X, \mathbb {F}_2)=0$
. Then the following conditions are equivalent:
-
(i)
 $X$
is
$X$
is
 $c_1$
-maximal, i.e.
$c_1$
-maximal, i.e.
 $H^2_G(X, \mathbb {Z}(1)) \to H^2(X, \mathbb {F}_2)$
is surjective;
$H^2_G(X, \mathbb {Z}(1)) \to H^2(X, \mathbb {F}_2)$
is surjective;
-
(ii)
 $\textrm {rk} H^2(X, \mathbb {Z})^G=0$
;
$\textrm {rk} H^2(X, \mathbb {Z})^G=0$
; -
(iii)
 $X(\mathbb {R})$
is connected.
$X(\mathbb {R})$
is connected.
Proof.
The condition
![]() $H^1(X, \mathbb {F}_2)=0$
is equivalent to saying that
$H^1(X, \mathbb {F}_2)=0$
is equivalent to saying that
![]() $b_1(X)=b_3(X)=0$
and
$b_1(X)=b_3(X)=0$
and
![]() $H^*(X, \mathbb {Z})$
is 2-torsion-free.
$H^*(X, \mathbb {Z})$
is 2-torsion-free.
For
![]() $({\rm i}) \Leftrightarrow {\rm (ii)}$
, by the Leray–Serre spectral sequence (3), together with the fact that
$({\rm i}) \Leftrightarrow {\rm (ii)}$
, by the Leray–Serre spectral sequence (3), together with the fact that
![]() $H^1(X, \mathbb {Z})=0$
(since
$H^1(X, \mathbb {Z})=0$
(since
![]() $b_1=0$
), we have an exact sequence
$b_1=0$
), we have an exact sequence
Since
![]() $H^2(G, \mathbb {Z}(1))=0$
and
$H^2(G, \mathbb {Z}(1))=0$
and
![]() $H^3(G, \mathbb {Z}(1))\to H^3_G(X, \mathbb {Z}(1))$
is injective by Lemma 2.2 (
$H^3(G, \mathbb {Z}(1))\to H^3_G(X, \mathbb {Z}(1))$
is injective by Lemma 2.2 (
![]() $X(\mathbb {R})\neq \emptyset$
since
$X(\mathbb {R})\neq \emptyset$
since
![]() $X$
is maximal), the natural map
$X$
is maximal), the natural map
![]() $H^2_G(X, \mathbb {Z}(1))\to H^2(X, \mathbb {Z}(1))^G$
is an isomorphism. Hence the natural map
$H^2_G(X, \mathbb {Z}(1))\to H^2(X, \mathbb {Z}(1))^G$
is an isomorphism. Hence the natural map
![]() $H^2_G(X, \mathbb {Z}(1))\to H^2(X, \mathbb {F}_2)$
factorizes as follows:
$H^2_G(X, \mathbb {Z}(1))\to H^2(X, \mathbb {F}_2)$
factorizes as follows:
By Lemma 2.4,
Since
![]() $H^2(X, \mathbb {F}_2)=H^2(X, \mathbb {Z})\otimes \mathbb {F}_2$
, the surjectivity of (17) (i.e. the
$H^2(X, \mathbb {F}_2)=H^2(X, \mathbb {Z})\otimes \mathbb {F}_2$
, the surjectivity of (17) (i.e. the
![]() $c_1$
-maximality) is equivalent to the vanishing of
$c_1$
-maximality) is equivalent to the vanishing of
![]() $H^2(X, \mathbb {Z})^G\otimes \mathbb {F}_2$
or, equivalently, since
$H^2(X, \mathbb {Z})^G\otimes \mathbb {F}_2$
or, equivalently, since
![]() $H^2(X, \mathbb {Z})^G$
is 2-torsion-free,
$H^2(X, \mathbb {Z})^G$
is 2-torsion-free,
![]() $H^2(X, \mathbb {Z})^G$
is of rank zero.
$H^2(X, \mathbb {Z})^G$
is of rank zero.
For
![]() ${\rm (ii)}\Rightarrow {\rm (iii)}$
, supposing the contrary that
${\rm (ii)}\Rightarrow {\rm (iii)}$
, supposing the contrary that
![]() $X(\mathbb {R})$
is disconnected, one can take two points
$X(\mathbb {R})$
is disconnected, one can take two points
![]() $x, y$
belonging to distinct components of
$x, y$
belonging to distinct components of
![]() $X(\mathbb {R})$
. Let
$X(\mathbb {R})$
. Let
![]() $\gamma$
be a path from
$\gamma$
be a path from
![]() $x$
to
$x$
to
![]() $y$
. Then
$y$
. Then
![]() $\gamma -\sigma _*(\gamma )$
is a 1-cycle in
$\gamma -\sigma _*(\gamma )$
is a 1-cycle in
![]() $X$
. Since
$X$
. Since
![]() $H_1(X, \mathbb {Z})$
is of odd torsion, there exists an odd number
$H_1(X, \mathbb {Z})$
is of odd torsion, there exists an odd number
![]() $N$
such that
$N$
such that
![]() $N(\gamma -\sigma _*(\gamma ))$
is a boundary of a 2-chain
$N(\gamma -\sigma _*(\gamma ))$
is a boundary of a 2-chain
![]() $T$
, i.e.
$T$
, i.e.
Then
![]() $T+\sigma _*(T)$
is a 2-cycle,
$T+\sigma _*(T)$
is a 2-cycle,
![]() $\sigma$
-invariant. Moreover, its class in
$\sigma$
-invariant. Moreover, its class in
![]() $H_2(X, \mathbb {Z})$
is non-torsion, since the intersection number of
$H_2(X, \mathbb {Z})$
is non-torsion, since the intersection number of
![]() $T+\sigma _*(T)$
with the connected component of
$T+\sigma _*(T)$
with the connected component of
![]() $S(\mathbb {R})$
containing
$S(\mathbb {R})$
containing
![]() $x$
is odd. We thus obtain a free class in
$x$
is odd. We thus obtain a free class in
![]() $H_2(X, \mathbb {Z})^G$
, a contradiction.
$H_2(X, \mathbb {Z})^G$
, a contradiction.
For
![]() ${\rm (iii)}\Rightarrow {\rm (ii)}$
, assuming
${\rm (iii)}\Rightarrow {\rm (ii)}$
, assuming
![]() $X(\mathbb {R})$
is connected, the maximality of
$X(\mathbb {R})$
is connected, the maximality of
![]() $X$
implies that
$X$
implies that
Consider the Viro homomorphism (see [Reference Degtyarev, Itenberg and KharlamovDIK00, Section 1.5]),
which is, roughly speaking, defined as follows: for a two-dimensional
![]() $\sigma$
-invariant oriented real submanifold
$\sigma$
-invariant oriented real submanifold
![]() $\Sigma \subset X$
such that
$\Sigma \subset X$
such that
![]() $\sigma$
reverses its orientation,
$\sigma$
reverses its orientation,
![]() $\operatorname {bv}$
sends the class
$\operatorname {bv}$
sends the class
![]() $[\Sigma ]\in H_2(X, \mathbb {Z}(1))^G$
to the class of the smooth curve
$[\Sigma ]\in H_2(X, \mathbb {Z}(1))^G$
to the class of the smooth curve
![]() $\Sigma \cap X(\mathbb {R})$
in
$\Sigma \cap X(\mathbb {R})$
in
![]() $H_2(X(\mathbb {R}), \mathbb {F}_2)$
.
$H_2(X(\mathbb {R}), \mathbb {F}_2)$
.
We claim that the Viro homomorphism
![]() $\operatorname {bv}$
is surjective. Indeed, for any 1-cycle
$\operatorname {bv}$
is surjective. Indeed, for any 1-cycle
![]() $\gamma$
representing a class
$\gamma$
representing a class
![]() $H_1(X(\mathbb {R}), \mathbb {F}_2)$
, its image inside
$H_1(X(\mathbb {R}), \mathbb {F}_2)$
, its image inside
![]() $H_1(X, \mathbb {Z})$
is of odd torsion. Hence there is an odd number
$H_1(X, \mathbb {Z})$
is of odd torsion. Hence there is an odd number
![]() $N$
such that the class of
$N$
such that the class of
![]() $N\gamma$
vanishes, i.e. there exists a 2-chain
$N\gamma$
vanishes, i.e. there exists a 2-chain
![]() $T$
in
$T$
in
![]() $X$
such that
$X$
such that
![]() $\partial T=N\gamma$
. Then
$\partial T=N\gamma$
. Then
![]() $T-\sigma _*(T)$
is a 2-cycle,
$T-\sigma _*(T)$
is a 2-cycle,
![]() $\sigma$
-anti-invariant, and hence defines an element in
$\sigma$
-anti-invariant, and hence defines an element in
![]() $H^2(X, \mathbb {Z}(1))^G$
, which is a preimage of
$H^2(X, \mathbb {Z}(1))^G$
, which is a preimage of
![]() $[\gamma ]$
. The surjectivity of the Viro homomorphism implies that
$[\gamma ]$
. The surjectivity of the Viro homomorphism implies that
![]() $\textrm {rk} H^2(X, \mathbb {Z}(1))^G\geqslant \dim H^1(X(\mathbb {R}), \mathbb {F}_2)$
. Therefore, we must have
$\textrm {rk} H^2(X, \mathbb {Z}(1))^G\geqslant \dim H^1(X(\mathbb {R}), \mathbb {F}_2)$
. Therefore, we must have
![]() $\textrm {rk} H^2(X, \mathbb {Z})^G=0$
.
$\textrm {rk} H^2(X, \mathbb {Z})^G=0$
.
Lemma 4.5.
A maximal
![]() $\mathbb {R}$
-rational real surface is K-maximal and
$\mathbb {R}$
-rational real surface is K-maximal and
![]() $c_1$
-maximal.
$c_1$
-maximal.
Proof. The minimal model theory for surfaces has its real version: any smooth projective real surface can be obtained from a minimalFootnote 7 one by a sequence of successive blow-ups, where at each step the blow-up center is either a point in the real locus or a pair of complex conjugate points outside of the real locus; see [Reference KollárKol01].
Note that, given a maximal surface
![]() $S$
, (any of) its minimal model
$S$
, (any of) its minimal model
![]() $S_0$
is again maximal by Proposition 3.8. Moreover, at each step of blow-up in
$S_0$
is again maximal by Proposition 3.8. Moreover, at each step of blow-up in
![]() $S=S_n\to \cdots \to S_1\to S_0$
, the blow-up center must be a point in the real locus (otherwise
$S=S_n\to \cdots \to S_1\to S_0$
, the blow-up center must be a point in the real locus (otherwise
![]() $b_2(S_{i+1}, \mathbb {F}_2)-b_2(S_i, \mathbb {F}_2)=2$
, but the real locus does not change). Therefore, any maximal real surface can be obtained from a maximal minimal real surface, via a sequence of blow-ups at points in the real loci. Since blowing up at a point in the real locus preserves the K-maximality, we only need to check that, for any minimal rational real surface, maximality implies K-maximality (which implies
$b_2(S_{i+1}, \mathbb {F}_2)-b_2(S_i, \mathbb {F}_2)=2$
, but the real locus does not change). Therefore, any maximal real surface can be obtained from a maximal minimal real surface, via a sequence of blow-ups at points in the real loci. Since blowing up at a point in the real locus preserves the K-maximality, we only need to check that, for any minimal rational real surface, maximality implies K-maximality (which implies
![]() $c_1$
-maximality by Lemma 4.3).
$c_1$
-maximality by Lemma 4.3).
By classification (see [Reference MangolteMan20, Theorem 4.3.23 and Theorem 4.4.11]), minimal rational real surfaces that are maximal are
![]() $\mathbb {P}^2$
,
$\mathbb {P}^2$
,
![]() $\mathbb {P}^1\times _{\mathbb {R}} \mathbb {P}^1$
and
$\mathbb {P}^1\times _{\mathbb {R}} \mathbb {P}^1$
and
![]() $\mathbb {F}_n$
(real Hirzebruch surface) for
$\mathbb {F}_n$
(real Hirzebruch surface) for
![]() $n\geqslant 2$
. For each surface
$n\geqslant 2$
. For each surface
![]() $S$
in the list,
$S$
in the list,
![]() $\textrm {KU}^1(S)=0$
and
$\textrm {KU}^1(S)=0$
and
![]() $\textrm {KU}^0(S)$
is generated by real algebraic line bundles:
$\textrm {KU}^0(S)$
is generated by real algebraic line bundles:
- for
![]() $\mathbb {P}^2$
, the generators are
$\mathbb {P}^2$
, the generators are
![]() $\mathcal {O}, \mathcal {O}(1), \mathcal {O}(2)$
;
$\mathcal {O}, \mathcal {O}(1), \mathcal {O}(2)$
;
- for
![]() $\mathbb {P}^1\times \mathbb {P}^1$
, the generators are
$\mathbb {P}^1\times \mathbb {P}^1$
, the generators are
![]() $\mathcal {O},p_1^* \mathcal {O}(1), p_2^* \mathcal {O}(1), p_1^* \mathcal {O}(1)\otimes p_2^* \mathcal {O}(1)$
;
$\mathcal {O},p_1^* \mathcal {O}(1), p_2^* \mathcal {O}(1), p_1^* \mathcal {O}(1)\otimes p_2^* \mathcal {O}(1)$
;
- for
![]() $\mathbb {F}_n=\mathbb {P}_{\mathbb {P}^1}(\mathcal {O}\oplus \mathcal {O}(n))\xrightarrow {\pi } \mathbb {P}^1$
, the generators are
$\mathbb {F}_n=\mathbb {P}_{\mathbb {P}^1}(\mathcal {O}\oplus \mathcal {O}(n))\xrightarrow {\pi } \mathbb {P}^1$
, the generators are
![]() $\mathcal {O}, \pi ^*\mathcal {O}_{\mathbb {P}^1}(1), \mathcal {O}_\pi (1), \pi ^*\mathcal {O}_{\mathbb {P}^1}(1)\otimes \mathcal {O}_{\pi }(1)$
.
$\mathcal {O}, \pi ^*\mathcal {O}_{\mathbb {P}^1}(1), \mathcal {O}_\pi (1), \pi ^*\mathcal {O}_{\mathbb {P}^1}(1)\otimes \mathcal {O}_{\pi }(1)$
.
Hence
![]() $\textrm {KR}^0(S)\to \textrm {KU}^0(S)$
is surjective.
$\textrm {KR}^0(S)\to \textrm {KU}^0(S)$
is surjective.
5. Moduli spaces of vector bundles on curves
Let
![]() $C$
be a compact Riemann surface of genus
$C$
be a compact Riemann surface of genus
![]() $g\geqslant 2$
. Let
$g\geqslant 2$
. Let
![]() $n\gt 0$
and
$n\gt 0$
and
![]() $d$
be two coprime integers. Let
$d$
be two coprime integers. Let
![]() $M:=M_C(n, d)$
be the moduli space of stable vector bundles of rank
$M:=M_C(n, d)$
be the moduli space of stable vector bundles of rank
![]() $n$
and degree
$n$
and degree
![]() $d$
. Since
$d$
. Since
![]() $n$
and
$n$
and
![]() $d$
are assumed to be coprime,
$d$
are assumed to be coprime,
![]() $M$
is a projective complex manifold of dimension
$M$
is a projective complex manifold of dimension
![]() $n^2(g-1)+1$
and there exists a universal bundle
$n^2(g-1)+1$
and there exists a universal bundle
![]() $\mathcal {E}$
on
$\mathcal {E}$
on
![]() $C\times M$
. We denote by
$C\times M$
. We denote by
![]() $p\colon C\times M\to C$
and
$p\colon C\times M\to C$
and
![]() $\pi \colon C\times M\to M$
the two natural projections.
$\pi \colon C\times M\to M$
the two natural projections.
We will use the following fundamental theorem of Atiyah and Bott [Reference Atiyah and BottAB83, Theorem 9.11] on generators of the cohomology ring of
![]() $M$
.
$M$
.
Theorem 5.1 (Atiyah–Bott). Assume that
![]() $d\gt (2g-2)n$
. The cohomology ring
$d\gt (2g-2)n$
. The cohomology ring
![]() $H^*(M, \mathbb {Z})$
is torsion-free and generated by the following three types of elements.
$H^*(M, \mathbb {Z})$
is torsion-free and generated by the following three types of elements.
-
(i) For
 $1\leqslant r\leqslant n$
, the Chern class
$1\leqslant r\leqslant n$
, the Chern class
 $a_r:=c_r(\mathcal {E}|_M)\in H^{2r}(M, \mathbb {Z})$
, where
$a_r:=c_r(\mathcal {E}|_M)\in H^{2r}(M, \mathbb {Z})$
, where
 $\mathcal {E}|_M$
is the restriction of
$\mathcal {E}|_M$
is the restriction of
 $\mathcal {E}$
to a fiber of
$\mathcal {E}$
to a fiber of
 $p$
.
$p$
. -
(ii) For
 $1\leqslant r\leqslant n$
, the
$1\leqslant r\leqslant n$
, the
 $(1, 2r-1)$
-Künneth components
$(1, 2r-1)$
-Künneth components
 $b_{r,j}\in H^{2r-1}(M, \mathbb {Z})$
of
$b_{r,j}\in H^{2r-1}(M, \mathbb {Z})$
of
 $c_r(\mathcal {E})$
, where we write
$c_r(\mathcal {E})$
, where we write
 $c_r(\mathcal {E})=\sum _{j=1}^{2g} \alpha _j\otimes b_{r, j}+1_C\otimes a_r+ [\textrm {pt}]\otimes \pi _*(c_r(\mathcal {E}))$
, where
$c_r(\mathcal {E})=\sum _{j=1}^{2g} \alpha _j\otimes b_{r, j}+1_C\otimes a_r+ [\textrm {pt}]\otimes \pi _*(c_r(\mathcal {E}))$
, where
 $\{\alpha _j\}_{1\leqslant j\leqslant 2g}$
form a basis of
$\{\alpha _j\}_{1\leqslant j\leqslant 2g}$
form a basis of
 $H^1(C, \mathbb {Z})$
,
$H^1(C, \mathbb {Z})$
,
 $1_C$
is the fundamental class of
$1_C$
is the fundamental class of
 $C$
and
$C$
and
 $[\textrm {pt}]$
is the class of a point on
$[\textrm {pt}]$
is the class of a point on
 $C$
.
$C$
. -
(iii) For
 $1\leqslant r\leqslant d+n(1-g)$
, the Chern class
$1\leqslant r\leqslant d+n(1-g)$
, the Chern class
 $c_r(\pi _*\mathcal {E})\in H^{2r}(M, \mathbb {Z})$
.
$c_r(\pi _*\mathcal {E})\in H^{2r}(M, \mathbb {Z})$
.
Remark 5.2. In the above theorem, note that under the numerical assumption
![]() $d\gt (2g-2)n$
, we have
$d\gt (2g-2)n$
, we have
![]() $R^1\pi _*\mathcal {E}=0$
and
$R^1\pi _*\mathcal {E}=0$
and
![]() $\pi _*\mathcal {E}$
is a vector bundle of rank
$\pi _*\mathcal {E}$
is a vector bundle of rank
![]() $d+n(1-g)$
by the Riemann–Roch theorem. This assumption can be dropped in the statement provided that in (iii) we replace the direct image
$d+n(1-g)$
by the Riemann–Roch theorem. This assumption can be dropped in the statement provided that in (iii) we replace the direct image
![]() $\pi _*\mathcal {E}$
by the K-theoretic push-forward
$\pi _*\mathcal {E}$
by the K-theoretic push-forward
![]() $\pi _!\mathcal {E}:=\sum _i (-1)^i[R^i\pi _*\mathcal {E}]$
and allow
$\pi _!\mathcal {E}:=\sum _i (-1)^i[R^i\pi _*\mathcal {E}]$
and allow
![]() $r$
to be any integer.
$r$
to be any integer.
Now, let
![]() $\sigma$
be a real structure on the curve
$\sigma$
be a real structure on the curve
![]() $C$
. It naturally induces a real structure
$C$
. It naturally induces a real structure
![]() $\sigma _M$
on
$\sigma _M$
on
![]() $M$
, given by the anti-holomorphic involution sending
$M$
, given by the anti-holomorphic involution sending
![]() $E$
to
$E$
to
![]() $\overline {\sigma ^*(E)}$
(indeed, the rank and the degree are both preserved by
$\overline {\sigma ^*(E)}$
(indeed, the rank and the degree are both preserved by
![]() $\sigma _M$
). We give a short proof of the following theorem of Brugallé and Schaffhauser [Reference Brugallé and SchaffhauserBS22, Theorem 1.2], which is based on previous works of Earl and Kirwan [Reference Earl and KirwanEK00], Schaffhauser [Reference SchaffhauserSch12] and Liu and Schaffhauser [Reference Liu and SchaffhauserLS13].
$\sigma _M$
). We give a short proof of the following theorem of Brugallé and Schaffhauser [Reference Brugallé and SchaffhauserBS22, Theorem 1.2], which is based on previous works of Earl and Kirwan [Reference Earl and KirwanEK00], Schaffhauser [Reference SchaffhauserSch12] and Liu and Schaffhauser [Reference Liu and SchaffhauserLS13].
Theorem 5.3.
Let
![]() $(C, \sigma )$
be a smooth projective real curve. If
$(C, \sigma )$
be a smooth projective real curve. If
![]() $(C, \sigma )$
is maximal, then
$(C, \sigma )$
is maximal, then
![]() $(M, \sigma _M)$
is also maximal. Conversely, if
$(M, \sigma _M)$
is also maximal. Conversely, if
![]() $(M, \sigma _M)$
is maximal and
$(M, \sigma _M)$
is maximal and
![]() $C(\mathbb {R})\neq \emptyset$
, then
$C(\mathbb {R})\neq \emptyset$
, then
![]() $(C, \sigma )$
is maximal.
$(C, \sigma )$
is maximal.
Proof.
For simplicity, we drop the real structures from the notation. First, we assume that
![]() $C$
is maximal and prove the maximality of
$C$
is maximal and prove the maximality of
![]() $M$
. Tensoring with an algebraic
$M$
. Tensoring with an algebraic
![]() $\mathbb {R}$
-line bundle
$\mathbb {R}$
-line bundle
![]() $\mathcal {L}$
on
$\mathcal {L}$
on
![]() $C$
of positive degree induces an isomorphism of moduli spaces that is compatible with the real structures (in particular, the maximality is preserved):
$C$
of positive degree induces an isomorphism of moduli spaces that is compatible with the real structures (in particular, the maximality is preserved):
We can therefore assume that
![]() $d\gt (2g-2)n$
.
$d\gt (2g-2)n$
.
By passing to the
![]() $\mathbb {F}_2$
-coefficient in Theorem5.1, we get a set of generators for the ring
$\mathbb {F}_2$
-coefficient in Theorem5.1, we get a set of generators for the ring
![]() $H^*_G(M, \mathbb {F}_2)$
. We will show that they are all in the image of the restriction map
$H^*_G(M, \mathbb {F}_2)$
. We will show that they are all in the image of the restriction map
![]() $H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
. The key point is that the universal bundle
$H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
. The key point is that the universal bundle
![]() $\mathcal {E}$
is a real algebraic/holomorphic vector bundle on the real variety
$\mathcal {E}$
is a real algebraic/holomorphic vector bundle on the real variety
![]() $C\times M$
, and hence defines a class
$C\times M$
, and hence defines a class
![]() $[\mathcal {E}]\in \textrm {KR}^0(C\times M)$
and possesses equivariant Chern classes
$[\mathcal {E}]\in \textrm {KR}^0(C\times M)$
and possesses equivariant Chern classes
![]() $c^G_r(\mathcal {E})\in H^{2r}_G(C\times M, \mathbb {F}_2)$
for any
$c^G_r(\mathcal {E})\in H^{2r}_G(C\times M, \mathbb {F}_2)$
for any
![]() $r\in \mathbb {N}$
.
$r\in \mathbb {N}$
.
- For the generators in (i) and (ii), they are all of the form
![]() $[c_r(\mathcal {E})]_*(\alpha ):=\pi _*( p^*(\alpha )\smile c_r(\mathcal {E}))$
, where
$[c_r(\mathcal {E})]_*(\alpha ):=\pi _*( p^*(\alpha )\smile c_r(\mathcal {E}))$
, where
![]() $\alpha \in H^*(C, \mathbb {F}_2)$
, upon which the Chern class
$\alpha \in H^*(C, \mathbb {F}_2)$
, upon which the Chern class
![]() $c_r(\mathcal {E})\in H^*(C\times M, \mathbb {F}_2)$
acts as cohomological correspondence. Since we have the commutative diagram
$c_r(\mathcal {E})\in H^*(C\times M, \mathbb {F}_2)$
acts as cohomological correspondence. Since we have the commutative diagram

where the left vertical arrow is surjective by the maximality of
![]() $C$
(and Proposition 2.3), we obtain that
$C$
(and Proposition 2.3), we obtain that
![]() $[c_r(\mathcal {E})]_*(\alpha )$
lies in the image of
$[c_r(\mathcal {E})]_*(\alpha )$
lies in the image of
![]() $H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
.
$H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
.
- For the generators in (iii), consider the commutative diagram (for any
![]() $r\in \mathbb {N}$
)
$r\in \mathbb {N}$
)

where the left horizontal arrows are the K-theoretic push-forwards along the projection
![]() $\pi \colon C\times M\to M$
(which is a real map). Recall that
$\pi \colon C\times M\to M$
(which is a real map). Recall that
![]() $[\mathcal {E}]\in \textrm {KR}^0(C\times M)$
is mapped to
$[\mathcal {E}]\in \textrm {KR}^0(C\times M)$
is mapped to
![]() $[\mathcal {E}]\in \textrm {KU}^0(C\times M)$
. Therefore,
$[\mathcal {E}]\in \textrm {KU}^0(C\times M)$
. Therefore,
![]() $c_r(\pi _*(\mathcal {E}))=c_r(\pi _![\mathcal {E}])$
(see Remark 5.2), which naturally lies in the image of
$c_r(\pi _*(\mathcal {E}))=c_r(\pi _![\mathcal {E}])$
(see Remark 5.2), which naturally lies in the image of
![]() $H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
.
$H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
.
Consequently,
![]() $H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
is surjective. We conclude the maximality of
$H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
is surjective. We conclude the maximality of
![]() $M$
by Proposition 2.3.
$M$
by Proposition 2.3.
Conversely, assuming that
![]() $M$
is maximal, then by Proposition 3.10 and the fact that
$M$
is maximal, then by Proposition 3.10 and the fact that
![]() $H^*(M, \mathbb {Z})$
is torsion-free, we get the maximality of the Albanese variety of
$H^*(M, \mathbb {Z})$
is torsion-free, we get the maximality of the Albanese variety of
![]() $M$
, which is identified with
$M$
, which is identified with
![]() $J^d(C)$
. Since
$J^d(C)$
. Since
![]() $C(\mathbb {R})\neq \emptyset$
by our hypothesis, tensoring with a degree-1 real line bundle shows that
$C(\mathbb {R})\neq \emptyset$
by our hypothesis, tensoring with a degree-1 real line bundle shows that
![]() $J(C)$
is isomorphic to
$J(C)$
is isomorphic to
![]() $J^d(C)$
, and hence is also maximal. By Corollary 3.12,
$J^d(C)$
, and hence is also maximal. By Corollary 3.12,
![]() $C$
is maximal.
$C$
is maximal.
Remark 5.4.
-
(i) Brugallé and Schaffhauser [Reference Brugallé and SchaffhauserBS22] also proved that, for a
 $\mathbb {R}$
-line bundle
$\mathbb {R}$
-line bundle
 $\mathcal {L}$
on a maximal real curve
$\mathcal {L}$
on a maximal real curve
 $C$
, the moduli space
$C$
, the moduli space
 $M_C(n, \mathcal {L})$
of stable bundles with fixed determinant is also maximal.
$M_C(n, \mathcal {L})$
of stable bundles with fixed determinant is also maximal. -
(ii) Brugallé and Schaffhauser [Reference Brugallé and SchaffhauserBS22] actually shows that
 $M_C(n, d)$
and
$M_C(n, d)$
and
 $M_C(n, \mathcal {L})$
satisfy a stronger property called Hodge-expressivity provided
$M_C(n, \mathcal {L})$
satisfy a stronger property called Hodge-expressivity provided
 $C$
is maximal. Our proof does not give any information on this regard; the reason is partially explained in Remark 11.8.
$C$
is maximal. Our proof does not give any information on this regard; the reason is partially explained in Remark 11.8.
Moduli spaces of parabolic vector bundles were introduced and studied by Mehta and Seshadri [Reference Mehta and SeshadriMS80]. Theorem5.3 admits the following consequence in this context.
Corollary 5.5 (Moduli of parabolic bundles). Let
![]() $C$
be a maximal real curve. Fix a (finite) set
$C$
be a maximal real curve. Fix a (finite) set
![]() $D\subset C(\mathbb {R})$
whose elements are called parabolic points. Let
$D\subset C(\mathbb {R})$
whose elements are called parabolic points. Let
![]() $n\gt 0$
and
$n\gt 0$
and
![]() $d$
be coprime integers. Let
$d$
be coprime integers. Let
![]() $\underline {1}$
denote the full flag type (at each point of
$\underline {1}$
denote the full flag type (at each point of
![]() $D$
), and let
$D$
), and let
![]() $\alpha$
be a generic weight. Then the moduli space
$\alpha$
be a generic weight. Then the moduli space
![]() $M^{\alpha }_{C, D}(n, d, \underline {1})$
of
$M^{\alpha }_{C, D}(n, d, \underline {1})$
of
![]() $\alpha$
-stable parabolic vector bundles of rank
$\alpha$
-stable parabolic vector bundles of rank
![]() $n$
, degree
$n$
, degree
![]() $d$
and full flag type is maximal.
$d$
and full flag type is maximal.
Proof.
By [Reference Boden and HuBH95], [Reference Boden and YokogawaBY99] and [Reference ThaddeusTha96], there is a wall-and-chamber structure on the space of weights and, by varying the weight, the moduli space stays the same within the chamber and undergoes a standard flip when crossing a wall with flipping centers being projective bundles over products of moduli spaces of stable parabolic bundles with smaller invariants (see [Reference Boden and YokogawaBY99, Theorem 4.1] or [Reference Fu, Hoskins and LehalleurFHPL23, Theorem 5.11]). Therefore, by wall-crossing, induction and Remark 3.6, we only need to prove the maximality of
![]() $M^{\alpha }_{C, D}(n, d, \underline {1})$
for
$M^{\alpha }_{C, D}(n, d, \underline {1})$
for
![]() $\alpha$
generic in the minimal chamber, where the stability of a parabolic bundle reduces to the stability of the underlying vector bundle. To this end, one uses natural morphisms which forget the flags. By [Reference Boden and YokogawaBY99, Theorem 4.2], such morphisms identify the moduli space of parabolic bundles as iterated flag bundles (hence iterated Grassmannian bundles) over
$\alpha$
generic in the minimal chamber, where the stability of a parabolic bundle reduces to the stability of the underlying vector bundle. To this end, one uses natural morphisms which forget the flags. By [Reference Boden and YokogawaBY99, Theorem 4.2], such morphisms identify the moduli space of parabolic bundles as iterated flag bundles (hence iterated Grassmannian bundles) over
![]() $M_C(n,d)$
. By Proposition 3.3 (or rather Remark 3.4) and Theorem5.3, we can conclude the maximality of
$M_C(n,d)$
. By Proposition 3.3 (or rather Remark 3.4) and Theorem5.3, we can conclude the maximality of
![]() $M^{\alpha }_{C, D}(n, d, \underline {1})$
.
$M^{\alpha }_{C, D}(n, d, \underline {1})$
.
6. Moduli spaces of Higgs bundles on curves
Let
![]() $C$
be smooth projective curve of genus
$C$
be smooth projective curve of genus
![]() $g\geqslant 2$
. A Higgs bundle on
$g\geqslant 2$
. A Higgs bundle on
![]() $C$
is a pair
$C$
is a pair
![]() $(E, \phi )$
where
$(E, \phi )$
where
![]() $E$
is a holomorphic vector bundle on
$E$
is a holomorphic vector bundle on
![]() $C$
and
$C$
and
![]() $\phi \colon E\to E\otimes \omega _C$
is
$\phi \colon E\to E\otimes \omega _C$
is
![]() $\mathcal {O}_C$
-linear. Such a pair
$\mathcal {O}_C$
-linear. Such a pair
![]() $(E, \phi )$
is said to be (semi-)stable if any proper Higgs sub-bundle
$(E, \phi )$
is said to be (semi-)stable if any proper Higgs sub-bundle
![]() $(E^{\prime}, \phi |_{E^{\prime}})$
satisfies the slope inequality
$(E^{\prime}, \phi |_{E^{\prime}})$
satisfies the slope inequality
![]() $\mu (E^{\prime})(\leqslant )\lt \mu (E)$
. Fix two integers
$\mu (E^{\prime})(\leqslant )\lt \mu (E)$
. Fix two integers
![]() $n\gt 0$
and
$n\gt 0$
and
![]() $d$
that are coprime to each other. Then stability and semi-stability coincide for Higgs bundles of rank
$d$
that are coprime to each other. Then stability and semi-stability coincide for Higgs bundles of rank
![]() $n$
and degree
$n$
and degree
![]() $d$
, and the moduli space
$d$
, and the moduli space
![]() $H_C(n, d)$
, constructed by Nitsure in [Reference NitsureNit91], of (semi-)stable Higgs bundles of rank
$H_C(n, d)$
, constructed by Nitsure in [Reference NitsureNit91], of (semi-)stable Higgs bundles of rank
![]() $n$
and degree
$n$
and degree
![]() $d$
is a smooth quasi-projective variety of dimension
$d$
is a smooth quasi-projective variety of dimension
![]() $2n^2(g-1)+2$
, admitting a hyper-Kähler metric and containing the cotangent bundle of
$2n^2(g-1)+2$
, admitting a hyper-Kähler metric and containing the cotangent bundle of
![]() $M_C(n, d)$
as an open subscheme. There is a so-called Hitchin map sending
$M_C(n, d)$
as an open subscheme. There is a so-called Hitchin map sending
![]() $(E, \phi )$
to the coefficients of the characteristic polynomial of
$(E, \phi )$
to the coefficients of the characteristic polynomial of
![]() $\phi$
:
$\phi$
:
 \begin{align*}H_C(n,d)\to \bigoplus _{i=1}^nH^0(C, \omega _C^{\otimes i}).\end{align*}
\begin{align*}H_C(n,d)\to \bigoplus _{i=1}^nH^0(C, \omega _C^{\otimes i}).\end{align*}
The Hitchin map is a proper map (see Hitchin [Reference HitchinHit87], Nitsure [Reference NitsureNit91] and Simpson [Reference SimpsonSim92, Proposition 1.4]). Hence
![]() $H_C(n,d)$
is a partial compactificationFootnote
8
of the cotangent bundle of
$H_C(n,d)$
is a partial compactificationFootnote
8
of the cotangent bundle of
![]() $M_C(n, d)$
. We refer to [Reference HitchinHit87] and [Reference SimpsonSim92] for more details.
$M_C(n, d)$
. We refer to [Reference HitchinHit87] and [Reference SimpsonSim92] for more details.
Markman constructed in [Reference MarkmanMar07, Theorem 3] a system of integral generators of the cohomology ring
![]() $H^*(H_C(n,d), \mathbb {Z})$
. By [Reference García-Prada and HeinlothGPH13, Corollary 9],
$H^*(H_C(n,d), \mathbb {Z})$
. By [Reference García-Prada and HeinlothGPH13, Corollary 9],
![]() $H^*(H_C(n,d), \mathbb {Z})$
is torsion-free, and hence Markman’s generators also give generators for
$H^*(H_C(n,d), \mathbb {Z})$
is torsion-free, and hence Markman’s generators also give generators for
![]() $H^*(H_C(n,d), \mathbb {F}_2)$
. We will need the following somewhat different characterizations of these integral generators, in a way closer to that in Atiyah and Bott’s Theorem5.1.
$H^*(H_C(n,d), \mathbb {F}_2)$
. We will need the following somewhat different characterizations of these integral generators, in a way closer to that in Atiyah and Bott’s Theorem5.1.
Theorem 6.1 (Integral generators for cohomology of Higgs moduli). Let
![]() $H:=H_C(n, d)$
be the moduli space of stable Higgs bundles of coprime rank
$H:=H_C(n, d)$
be the moduli space of stable Higgs bundles of coprime rank
![]() $n$
and degree
$n$
and degree
![]() $d$
. Let
$d$
. Let
![]() $\mathcal {E}$
be a universal bundle over
$\mathcal {E}$
be a universal bundle over
![]() $C \times H$
. Let
$C \times H$
. Let
![]() $p_1, p_2$
be the two projections from
$p_1, p_2$
be the two projections from
![]() $C\times H$
to its two factors. Then the cohomology ring
$C\times H$
to its two factors. Then the cohomology ring
![]() $H^*(H, \mathbb {Z})$
is torsion-free and generated by the following three types of elements.
$H^*(H, \mathbb {Z})$
is torsion-free and generated by the following three types of elements.
-
(i) For
 $1\leqslant r\leqslant n$
, the Chern class
$1\leqslant r\leqslant n$
, the Chern class
 $a_r:=c_r(\mathcal {E}|_H)\in H^{2r}(H, \mathbb {Z})$
, where
$a_r:=c_r(\mathcal {E}|_H)\in H^{2r}(H, \mathbb {Z})$
, where
 $\mathcal {E}|_H$
is the restriction of
$\mathcal {E}|_H$
is the restriction of
 $\mathcal {E}$
to a fiber of
$\mathcal {E}$
to a fiber of
 $p_1$
.
$p_1$
. -
(ii) For
 $1\leqslant r\leqslant n$
, the
$1\leqslant r\leqslant n$
, the
 $(1, 2r-1)$
-Künneth components
$(1, 2r-1)$
-Künneth components
 $b_{r,j}\in H^{2r-1}(H, \mathbb {Z})$
of
$b_{r,j}\in H^{2r-1}(H, \mathbb {Z})$
of
 $c_r(\mathcal {E})$
, where we write
$c_r(\mathcal {E})$
, where we write
 $c_r(\mathcal {E})=\sum _{j=1}^{2g} \alpha _j\otimes b_{r, j}+1_C\otimes a_r+ [\textrm {pt}]\otimes p_{2,*}(c_r(\mathcal {E}))$
via the Künneth formula, where
$c_r(\mathcal {E})=\sum _{j=1}^{2g} \alpha _j\otimes b_{r, j}+1_C\otimes a_r+ [\textrm {pt}]\otimes p_{2,*}(c_r(\mathcal {E}))$
via the Künneth formula, where
 $\{\alpha _j\}_{1\leqslant j\leqslant 2g}$
form a basis of
$\{\alpha _j\}_{1\leqslant j\leqslant 2g}$
form a basis of
 $H^1(C, \mathbb {Z})$
,
$H^1(C, \mathbb {Z})$
,
 $1_C$
is the fundamental class of
$1_C$
is the fundamental class of
 $C$
and
$C$
and
 $[\textrm {pt}]$
is the class of a point on
$[\textrm {pt}]$
is the class of a point on
 $C$
.
$C$
. -
(iii) For
 $r\geqslant 0$
, the Chern class
$r\geqslant 0$
, the Chern class
 $c_r(p_{2, !}[\mathcal {E}])\in H^{2r}(H, \mathbb {Z})$
, where
$c_r(p_{2, !}[\mathcal {E}])\in H^{2r}(H, \mathbb {Z})$
, where
 $[\mathcal {E}]$
is viewed as in
$[\mathcal {E}]$
is viewed as in
 $\textrm {KU}^0(C\times H)$
and
$\textrm {KU}^0(C\times H)$
and
 $p_{2,!}$
is the K-theoretic push-forward (Gysin map).
$p_{2,!}$
is the K-theoretic push-forward (Gysin map).
Proof.
As is mentioned above,
![]() $H^*(H, \mathbb {Z})$
is torsion-free thanks to [Reference García-Prada and HeinlothGPH13, Corollary 9].
$H^*(H, \mathbb {Z})$
is torsion-free thanks to [Reference García-Prada and HeinlothGPH13, Corollary 9].
The Atiyah–Hirzebruch spectral sequence
![]() $E_2^{p,q}=H^p(C, \textrm {KU}^q(\textrm {pt}))\Rightarrow \textrm {KU}^{p+q}(C)$
degenerates at the
$E_2^{p,q}=H^p(C, \textrm {KU}^q(\textrm {pt}))\Rightarrow \textrm {KU}^{p+q}(C)$
degenerates at the
![]() $E_2$
-page for dimension reasons. We obtain that:
$E_2$
-page for dimension reasons. We obtain that:
-
– the Chern character map
 $(\textrm {rk}, c_1)\colon \textrm {KU}^0(C)\xrightarrow {\cong } H^0(C, \mathbb {Z})\oplus H^2(C, \mathbb {Z})$
is an isomorphism;
$(\textrm {rk}, c_1)\colon \textrm {KU}^0(C)\xrightarrow {\cong } H^0(C, \mathbb {Z})\oplus H^2(C, \mathbb {Z})$
is an isomorphism; -
– the higher first Chern classFootnote 9 map
 $c_{\frac {1}{2}}\colon \textrm {KU}^1(C) \xrightarrow {\cong } H^1(C, \mathbb {Z})$
is an isomorphism.
$c_{\frac {1}{2}}\colon \textrm {KU}^1(C) \xrightarrow {\cong } H^1(C, \mathbb {Z})$
is an isomorphism.
As in the statement of the theorem, let
![]() $\{\alpha _i\}_{i=1}^{2g}$
be a basis of
$\{\alpha _i\}_{i=1}^{2g}$
be a basis of
![]() $H^1(C, \mathbb {Z})$
. We consider the following basis of
$H^1(C, \mathbb {Z})$
. We consider the following basis of
![]() $H^0(C, \mathbb {Z})\oplus H^2(C, \mathbb {Z})$
:
$H^0(C, \mathbb {Z})\oplus H^2(C, \mathbb {Z})$
:
Via the above Chern class isomorphisms, we lift
![]() $\{\alpha _i\}_{i=1}^{2g+2}$
to a basis
$\{\alpha _i\}_{i=1}^{2g+2}$
to a basis
![]() $\{x_i\}_{i=1}^{2g+2}$
of
$\{x_i\}_{i=1}^{2g+2}$
of
![]() $\textrm {KU}^*(C)$
. In particular,
$\textrm {KU}^*(C)$
. In particular,
![]() $c_{\frac {1}{2}}(x_i)=\alpha _i$
for
$c_{\frac {1}{2}}(x_i)=\alpha _i$
for
![]() $1\leqslant i\leqslant 2g$
, and
$1\leqslant i\leqslant 2g$
, and
![]() $x_{2g+1}$
(respectively,
$x_{2g+1}$
(respectively,
![]() $x_{2g+2}$
) is represented by a degree
$x_{2g+2}$
) is represented by a degree
![]() $g-1$
line bundle (respectively, by
$g-1$
line bundle (respectively, by
![]() $[\mathcal {O}_C]-[\mathcal {O}_C(-x)]$
for a point
$[\mathcal {O}_C]-[\mathcal {O}_C(-x)]$
for a point
![]() $x\in C$
).
$x\in C$
).
We can write the decomposition of the class
![]() $[\mathcal {E}]\in \textrm {KU}^0(C\times H)$
via the Künneth formula
$[\mathcal {E}]\in \textrm {KU}^0(C\times H)$
via the Künneth formula
![]() $\textrm {KU}^0(C\times H)=\textrm {KU}^1(C)\otimes \textrm {KU}^1(H)\oplus \textrm {KU}^0(C)\otimes \textrm {KU}^0(H)$
as follows:
$\textrm {KU}^0(C\times H)=\textrm {KU}^1(C)\otimes \textrm {KU}^1(H)\oplus \textrm {KU}^0(C)\otimes \textrm {KU}^0(H)$
as follows:
 \begin{align} [\mathcal {E}]=\sum _{i=1}^{2g+2}p_1^*(x_i)\otimes p_2^*(e_i),\ \end{align}
\begin{align} [\mathcal {E}]=\sum _{i=1}^{2g+2}p_1^*(x_i)\otimes p_2^*(e_i),\ \end{align}
where
![]() $e_i\in \textrm {KU}^*(H)$
. By Markman [Reference MarkmanMar07, Theorem 3], the (usual) Chern classes
$e_i\in \textrm {KU}^*(H)$
. By Markman [Reference MarkmanMar07, Theorem 3], the (usual) Chern classes
![]() $c_r(e_i)$
for
$c_r(e_i)$
for
![]() $i=2g+1$
and
$i=2g+1$
and
![]() $2g+2$
, and the higher Chern classes
$2g+2$
, and the higher Chern classes
![]() $c_{r-\frac {1}{2}}(e_i)$
for
$c_{r-\frac {1}{2}}(e_i)$
for
![]() $i\leqslant 2g$
, where
$i\leqslant 2g$
, where
![]() $r\in \mathbb {N}^*$
, generate the cohomology ring
$r\in \mathbb {N}^*$
, generate the cohomology ring
![]() $H^*(H, \mathbb {Z})$
. We will show that they all can be written in the form of generators in (i), (ii) and (iii) in the statement of the theorem:
$H^*(H, \mathbb {Z})$
. We will show that they all can be written in the form of generators in (i), (ii) and (iii) in the statement of the theorem:
- For the Chern classes of
![]() $e_{2g+2}$
, it is easy to check that when applying
$e_{2g+2}$
, it is easy to check that when applying
![]() $p_{2,!}$
to (20), on the right-hand side, the only contribution is the term
$p_{2,!}$
to (20), on the right-hand side, the only contribution is the term
![]() $p_{2,!}(p_1^*(x_{2g+2})\otimes p_2^*(e_{2g+2}))=\chi (x_{2g+2})e_{2g+2}=e_{2g+2}$
. Indeed,
$p_{2,!}(p_1^*(x_{2g+2})\otimes p_2^*(e_{2g+2}))=\chi (x_{2g+2})e_{2g+2}=e_{2g+2}$
. Indeed,
![]() $\chi (x_{2g+1})=0$
and
$\chi (x_{2g+1})=0$
and
![]() $\chi (x_{2g+2})=1$
by the Riemann–Roch theorem and the choices for
$\chi (x_{2g+2})=1$
by the Riemann–Roch theorem and the choices for
![]() $x_{2g+1}$
and
$x_{2g+1}$
and
![]() $x_{2g+2}$
. Therefore,
$x_{2g+2}$
. Therefore,
![]() $e_{2g+2}=p_{2, !}([\mathcal {E}])$
, and its Chern classes are included in (iii).
$e_{2g+2}=p_{2, !}([\mathcal {E}])$
, and its Chern classes are included in (iii).
- For the Chern classes of
![]() $e_{2g+1}$
, it is easy to check that when restricting both sides of (20) to a fiber of
$e_{2g+1}$
, it is easy to check that when restricting both sides of (20) to a fiber of
![]() $p_1$
, on the right-hand side, the only contribution comes from the term
$p_1$
, on the right-hand side, the only contribution comes from the term
![]() $p_1^*(x_{2g+1})\otimes p_2^*(e_{2g+1})$
, which restricts to
$p_1^*(x_{2g+1})\otimes p_2^*(e_{2g+1})$
, which restricts to
![]() $e_{2g+1}$
. Indeed, when restricting to a point of
$e_{2g+1}$
. Indeed, when restricting to a point of
![]() $C$
,
$C$
,
![]() $x_{2g+1}$
becomes
$x_{2g+1}$
becomes
![]() $1_{\textrm {pt}}$
and
$1_{\textrm {pt}}$
and
![]() $x_{2g+2}$
becomes zero. Therefore,
$x_{2g+2}$
becomes zero. Therefore,
![]() $e_{2g+1}=[\mathcal {E}]|_{H}$
, and its Chern classes are included in (i).
$e_{2g+1}=[\mathcal {E}]|_{H}$
, and its Chern classes are included in (i).
- For the higher Chern classes of
![]() $\{e_i\}_{i=1}^{2g}$
, take the
$\{e_i\}_{i=1}^{2g}$
, take the
![]() $(1, 2r-1)$
-Künneth component of the
$(1, 2r-1)$
-Künneth component of the
![]() $r$
th Chern classes of both sides of (20):
$r$
th Chern classes of both sides of (20):
 \begin{align*} &[c_r(\mathcal {E})]_{(1, 2r-1)}\\ =&\left [c_r\left (\sum _{i=1}^{2g+2}p_1^*(x_i)\otimes p_2^*(e_i)\right )\right ]_{(1, 2r-1)}\\ =&\left [c_r\left (\sum _{i=1}^{2g}p_1^*(x_i)\otimes p_2^*(e_i)\right )\right ]_{(1, 2r-1)}\\ =& \sum _{i=1}^{2g}\left [c_r\left (p_1^*(x_i)\otimes p_2^*(e_i)\right )\right ]_{(1, 2r-1)}\\ =& \sum _{i=1}^{2g} p_1^*c_{\frac {1}{2}}(x_i)\smile p_2^*c_{r-\frac {1}{2}}(e_i)\\ =& \sum _{i=1}^{2g} p_1^*\alpha _i\smile p_2^*c_{r-\frac {1}{2}}(e_i), \end{align*}
\begin{align*} &[c_r(\mathcal {E})]_{(1, 2r-1)}\\ =&\left [c_r\left (\sum _{i=1}^{2g+2}p_1^*(x_i)\otimes p_2^*(e_i)\right )\right ]_{(1, 2r-1)}\\ =&\left [c_r\left (\sum _{i=1}^{2g}p_1^*(x_i)\otimes p_2^*(e_i)\right )\right ]_{(1, 2r-1)}\\ =& \sum _{i=1}^{2g}\left [c_r\left (p_1^*(x_i)\otimes p_2^*(e_i)\right )\right ]_{(1, 2r-1)}\\ =& \sum _{i=1}^{2g} p_1^*c_{\frac {1}{2}}(x_i)\smile p_2^*c_{r-\frac {1}{2}}(e_i)\\ =& \sum _{i=1}^{2g} p_1^*\alpha _i\smile p_2^*c_{r-\frac {1}{2}}(e_i), \end{align*}
where the second equality follows from the fact that
![]() $x_{2g+1}, x_{2g+2}, e_{2g+1}, e_{2g+2}$
are in
$x_{2g+1}, x_{2g+2}, e_{2g+1}, e_{2g+2}$
are in
![]() $\textrm {KU}^0$
and hence do not have higher Chern classes in odd cohomology; the third equality is because
$\textrm {KU}^0$
and hence do not have higher Chern classes in odd cohomology; the third equality is because
![]() $c_r\left (\sum _{i=1}^{2g}p_1^*(x_i)\otimes p_2^*(e_i)\right )$
is a polynomial in higher Chern classes of
$c_r\left (\sum _{i=1}^{2g}p_1^*(x_i)\otimes p_2^*(e_i)\right )$
is a polynomial in higher Chern classes of
![]() $x_i$
and
$x_i$
and
![]() $e_i$
, but each
$e_i$
, but each
![]() $x_i$
can only contribute to
$x_i$
can only contribute to
![]() $c_{\frac {1}{2}}(x_i)\in H^1(C, \mathbb {Z})$
for the
$c_{\frac {1}{2}}(x_i)\in H^1(C, \mathbb {Z})$
for the
![]() $(1, 2r-1)$
-Künneth component, so only one of the
$(1, 2r-1)$
-Künneth component, so only one of the
![]() $x_i$
can contribute each time; the fourth equality follows from the explicit computation in [Reference MarkmanMar07], as is explained in the next lemma; the last equality is by the definition of the
$x_i$
can contribute each time; the fourth equality follows from the explicit computation in [Reference MarkmanMar07], as is explained in the next lemma; the last equality is by the definition of the
![]() $x_i$
. Therefore,
$x_i$
. Therefore,
![]() $c_{r-\frac {1}{2}}(e_i)$
is a Künneth component of
$c_{r-\frac {1}{2}}(e_i)$
is a Künneth component of
![]() $c_r(\mathcal {E})$
, which is included in (ii).
$c_r(\mathcal {E})$
, which is included in (ii).
To summarize, we have showed the Markman’s generators are indeed the ones in (i), (ii) and (iii) in the statement of the theorem.
Lemma 6.2.
Given a variety
![]() $H$
and a curve
$H$
and a curve
![]() $C$
, for any
$C$
, for any
![]() $x\in \textrm {KU}^1(C)$
and
$x\in \textrm {KU}^1(C)$
and
![]() $y\in \textrm {KU}^1(H)$
, we have
$y\in \textrm {KU}^1(H)$
, we have
for any positive integer
![]() $r$
.
$r$
.
Proof. Combining Markman [Reference MarkmanMar07, Lemma 22 (3)] and [Reference MarkmanMar07, the last formula in Section 2], we get
 \begin{align*}&c_r(p_1^*x\otimes p_2^*y)=\\& \sum _{\lambda ={(1^{m_1}\cdots s^{m_s})}\dashv r}(-1)^{r-\ell (\lambda )}\prod _{i\geqslant 1}(-1)^{m_i(i-1)}\sum _{0\leqslant k_1\lt \cdots \lt k_{m_i}\leqslant i-1}\prod _{j=1}^{m_i}\left(\begin{array}{c}{i-1}\\{k_j}\end{array}\right)p_1^*c_{k_j+\frac {1}{2}}(x)\smile p_2^*c_{i-k_j-\frac {1}{2}}(y).\end{align*}
\begin{align*}&c_r(p_1^*x\otimes p_2^*y)=\\& \sum _{\lambda ={(1^{m_1}\cdots s^{m_s})}\dashv r}(-1)^{r-\ell (\lambda )}\prod _{i\geqslant 1}(-1)^{m_i(i-1)}\sum _{0\leqslant k_1\lt \cdots \lt k_{m_i}\leqslant i-1}\prod _{j=1}^{m_i}\left(\begin{array}{c}{i-1}\\{k_j}\end{array}\right)p_1^*c_{k_j+\frac {1}{2}}(x)\smile p_2^*c_{i-k_j-\frac {1}{2}}(y).\end{align*}
On the right-hand side,
![]() $c_{k_j+\frac {1}{2}}(x)$
is non-zero only if
$c_{k_j+\frac {1}{2}}(x)$
is non-zero only if
![]() $k_j=0$
. Therefore, all
$k_j=0$
. Therefore, all
![]() $k_j=0$
, and hence
$k_j=0$
, and hence
![]() $m_i=0$
or 1 (i.e.
$m_i=0$
or 1 (i.e.
![]() $\lambda$
has no repeated parts), and the above formula simplifies to
$\lambda$
has no repeated parts), and the above formula simplifies to
 \begin{align*}c_r(p_1^*x\otimes p_2^*y)=\sum _{\lambda =(\lambda _1\gt \cdots \gt \lambda _{\ell })\dashv r}(-1)^{r-\ell }\prod _{j\geqslant 1}^{\ell }(-1)^{(\lambda _j-1)}p_1^*c_{\frac {1}{2}}(x)\smile p_2^*c_{i-\frac {1}{2}}(y).\end{align*}
\begin{align*}c_r(p_1^*x\otimes p_2^*y)=\sum _{\lambda =(\lambda _1\gt \cdots \gt \lambda _{\ell })\dashv r}(-1)^{r-\ell }\prod _{j\geqslant 1}^{\ell }(-1)^{(\lambda _j-1)}p_1^*c_{\frac {1}{2}}(x)\smile p_2^*c_{i-\frac {1}{2}}(y).\end{align*}
Now if we take the
![]() $(1, 2r-1)$
-Künneth component, for each term there can be at most one
$(1, 2r-1)$
-Künneth component, for each term there can be at most one
![]() $c_{\frac {1}{2}}(x)$
in the product, so only the trivial partition
$c_{\frac {1}{2}}(x)$
in the product, so only the trivial partition
![]() $\lambda =(r)$
contributes to this Künneth component, and we get the desired formula.
$\lambda =(r)$
contributes to this Künneth component, and we get the desired formula.
If
![]() $C$
is defined over
$C$
is defined over
![]() $\mathbb {R}$
, then so is
$\mathbb {R}$
, then so is
![]() $H_C(n, d)$
by construction. In other words, a real structure on
$H_C(n, d)$
by construction. In other words, a real structure on
![]() $C$
induces a natural real structure on
$C$
induces a natural real structure on
![]() $H_C(n, d)$
. We have the following analogue of Theorem5.3.
$H_C(n, d)$
. We have the following analogue of Theorem5.3.
Theorem 6.3.
Let
![]() $C$
be a smooth projective real curve. Let
$C$
be a smooth projective real curve. Let
![]() $n\gt 0$
and
$n\gt 0$
and
![]() $d$
be two coprime integers. If
$d$
be two coprime integers. If
![]() $C$
is maximal, then the moduli space
$C$
is maximal, then the moduli space
![]() $H_C(n, d)$
is also maximal. Conversely, if
$H_C(n, d)$
is also maximal. Conversely, if
![]() $H_C(n, d)$
is maximal and
$H_C(n, d)$
is maximal and
![]() $C(\mathbb {R})\neq \emptyset$
, then
$C(\mathbb {R})\neq \emptyset$
, then
![]() $C$
is maximal.
$C$
is maximal.
7. Hilbert squares and Hilbert cubes
Given a smooth complex variety
![]() $X$
and a positive integer
$X$
and a positive integer
![]() $n$
, the Hilbert scheme of length
$n$
, the Hilbert scheme of length
![]() $n$
subschemes on
$n$
subschemes on
![]() $X$
is called the
$X$
is called the
![]() $n$
th punctual Hilbert scheme of
$n$
th punctual Hilbert scheme of
![]() $X$
, denoted by
$X$
, denoted by
![]() $X^{[n]}$
or
$X^{[n]}$
or
![]() $\textrm {Hilb}_n(X)$
, which is a proper (respectively, projective) scheme if
$\textrm {Hilb}_n(X)$
, which is a proper (respectively, projective) scheme if
![]() $X$
is proper (respectively, projective). When
$X$
is proper (respectively, projective). When
![]() $\dim (X)=1$
,
$\dim (X)=1$
,
![]() $X^{[n]}$
is nothing but the symmetric power
$X^{[n]}$
is nothing but the symmetric power
![]() $ X^{(n)}$
, which is smooth. When
$ X^{(n)}$
, which is smooth. When
![]() $\dim (X)=2$
,
$\dim (X)=2$
,
![]() $X^{[n]}$
is again smooth by Fogarty [Reference FogartyFog68] and it provides a crepant resolution of the symmetric power
$X^{[n]}$
is again smooth by Fogarty [Reference FogartyFog68] and it provides a crepant resolution of the symmetric power
![]() $X^{(n)}$
via the Hilbert–Chow morphism. When
$X^{(n)}$
via the Hilbert–Chow morphism. When
![]() $\dim (X)\geqslant 3$
, by Cheah [Reference CheahChe98],
$\dim (X)\geqslant 3$
, by Cheah [Reference CheahChe98],
![]() $X^{[2]}$
and
$X^{[2]}$
and
![]() $X^{[3]}$
are still smooth, but
$X^{[3]}$
are still smooth, but
![]() $X^{[n]}$
are singular for
$X^{[n]}$
are singular for
![]() $n\geqslant 4$
.
$n\geqslant 4$
.
More generally, for any sequence of positive integers
![]() $n_1\lt n_2\lt \cdots \lt n_r$
, we have the so-called nested punctual Hilbert scheme
$n_1\lt n_2\lt \cdots \lt n_r$
, we have the so-called nested punctual Hilbert scheme
![]() $X^{[n_1, n_2, \ldots, n_r]}$
classifying flags of subschemes of lengths
$X^{[n_1, n_2, \ldots, n_r]}$
classifying flags of subschemes of lengths
![]() $n_1, \dots, n_r$
, defined as the incidence subscheme in the product
$n_1, \dots, n_r$
, defined as the incidence subscheme in the product
![]() $X^{[n_1]}\times \cdots \times X^{[n_r]}$
. Cheah [Reference CheahChe98] proved that, when
$X^{[n_1]}\times \cdots \times X^{[n_r]}$
. Cheah [Reference CheahChe98] proved that, when
![]() $\dim (X)\geqslant 3$
, the only smooth nested Hilbert schemes are
$\dim (X)\geqslant 3$
, the only smooth nested Hilbert schemes are
![]() $X$
,
$X$
,
![]() $X^{[1, 2]}$
,
$X^{[1, 2]}$
,
![]() $X^{[2]}$
,
$X^{[2]}$
,
![]() $X^{[3]}$
and
$X^{[3]}$
and
![]() $X^{[2,3]}$
.
$X^{[2,3]}$
.
Remark 7.1 (Explicit construction). We call
![]() $X^{[2]}$
the Hilbert square of
$X^{[2]}$
the Hilbert square of
![]() $X$
. One can construct
$X$
. One can construct
![]() $X^{[2]}$
simply as the blow-up of the (in general, singular) symmetric square
$X^{[2]}$
simply as the blow-up of the (in general, singular) symmetric square
![]() $X^{(2)}$
along the diagonal. An alternative way of construction is as follows: let
$X^{(2)}$
along the diagonal. An alternative way of construction is as follows: let
![]() $\textrm {Bl}_{\Delta }(X\times X)$
be the blow-up of
$\textrm {Bl}_{\Delta }(X\times X)$
be the blow-up of
![]() $X\times X$
along its diagonal, so then the natural involution on
$X\times X$
along its diagonal, so then the natural involution on
![]() $X\times X$
lifts to the blow-up and the quotient of
$X\times X$
lifts to the blow-up and the quotient of
![]() $\textrm {Bl}_{\Delta }(X\times X)$
by the involution is isomorphic to
$\textrm {Bl}_{\Delta }(X\times X)$
by the involution is isomorphic to
![]() $X^{[2]}$
.
$X^{[2]}$
.
Similarly, we call
![]() $X^{[3]}$
the Hilbert cube of
$X^{[3]}$
the Hilbert cube of
![]() $X$
. There is also a concrete construction for the Hilbert cube starting from
$X$
. There is also a concrete construction for the Hilbert cube starting from
![]() $X\times X\times X$
. Roughly, we first perform successive blow-ups in
$X\times X\times X$
. Roughly, we first perform successive blow-ups in
![]() $X^3$
to resolve the natural rational map
$X^3$
to resolve the natural rational map
![]() $X^3\dashrightarrow X^{[3]}$
, then quotient by the symmetric group
$X^3\dashrightarrow X^{[3]}$
, then quotient by the symmetric group
![]() $\mathfrak {S}_3$
and finally contract a divisor; see [Reference Shen and VialSV16] for the details.
$\mathfrak {S}_3$
and finally contract a divisor; see [Reference Shen and VialSV16] for the details.
Remark 7.2 (Douady spaces). The construction of Hilbert schemes can be generalized to the analytic category: for a complex manifold
![]() $X$
and a positive integer
$X$
and a positive integer
![]() $n$
, we have the so-called
$n$
, we have the so-called
![]() $n$
th punctual Douady space
$n$
th punctual Douady space
![]() $X^{[n]}$
, as well as the nested version. The aforementioned results of Cheah still hold in this setting: the only smooth nested punctual Douady spaces associated to a complex manifold
$X^{[n]}$
, as well as the nested version. The aforementioned results of Cheah still hold in this setting: the only smooth nested punctual Douady spaces associated to a complex manifold
![]() $X$
of dimension
$X$
of dimension
![]() $\geqslant 3$
are
$\geqslant 3$
are
![]() $X$
,
$X$
,
![]() $X^{[1, 2]}$
,
$X^{[1, 2]}$
,
![]() $X^{[2]}$
,
$X^{[2]}$
,
![]() $X^{[3]}$
and
$X^{[3]}$
and
![]() $X^{[2,3]}$
. In what follows, we will use the algebraic terminology Hilbert schemes (squares, cubes, etc.) to refer to their Douady analogues, and all the results in this section hold in the analytic category as well as in the algebraic category, with the same proof.
$X^{[2,3]}$
. In what follows, we will use the algebraic terminology Hilbert schemes (squares, cubes, etc.) to refer to their Douady analogues, and all the results in this section hold in the analytic category as well as in the algebraic category, with the same proof.
If
![]() $(X, \sigma )$
is a real variety, then
$(X, \sigma )$
is a real variety, then
![]() $\sigma$
naturally induces real structures on the nested punctual Hilbert schemes. Indeed, for a finite length closed subscheme
$\sigma$
naturally induces real structures on the nested punctual Hilbert schemes. Indeed, for a finite length closed subscheme
![]() $Z$
of
$Z$
of
![]() $X$
, consider the base change by the conjugate automorphism of the base field
$X$
, consider the base change by the conjugate automorphism of the base field
![]() $\mathbb {C}$
:
$\mathbb {C}$
:

Then define the image of
![]() $Z$
to be the closed subscheme
$Z$
to be the closed subscheme
![]() $\sigma \circ i^{\prime}: \bar {Z}\hookrightarrow S$
. In what follows, we always equip the (nested) Hilbert schemes with such natural real structures.
$\sigma \circ i^{\prime}: \bar {Z}\hookrightarrow S$
. In what follows, we always equip the (nested) Hilbert schemes with such natural real structures.
Theorem 7.3.
Let
![]() $X$
be a smooth real variety.
$X$
be a smooth real variety.
-
(i) If
 $X$
is maximal, then
$X$
is maximal, then
 $X^{[1, 2]}$
is maximal.
$X^{[1, 2]}$
is maximal.
-
(ii) If
 $X^{[2]}$
is maximal and
$X^{[2]}$
is maximal and
 $X(\mathbb {R})\neq \emptyset$
, then
$X(\mathbb {R})\neq \emptyset$
, then
 $X$
,
$X$
,
 $X^{[1, 2]}$
,
$X^{[1, 2]}$
,
 $X^{[2,3]}$
and
$X^{[2,3]}$
and
 $X^{[3]}$
are all maximal.
$X^{[3]}$
are all maximal.
Proof.
(i) It is easy to see that
![]() $X^{[1,2]}$
is isomorphic to
$X^{[1,2]}$
is isomorphic to
![]() $\textrm {Bl}_{\Delta }(X\times X)$
, the blow-up of
$\textrm {Bl}_{\Delta }(X\times X)$
, the blow-up of
![]() $X\times X$
along its diagonal, whose maximality follows from Lemma 3.1 and Proposition 3.5.
$X\times X$
along its diagonal, whose maximality follows from Lemma 3.1 and Proposition 3.5.
(ii) Denote by
![]() $\tau \colon \textrm {Bl}_{\Delta }(X\times X)\to X\times X$
and
$\tau \colon \textrm {Bl}_{\Delta }(X\times X)\to X\times X$
and
![]() $g\colon \textrm {Bl}_{\Delta }(X\times X)\to X^{[2]}$
the natural morphisms, both defined over
$g\colon \textrm {Bl}_{\Delta }(X\times X)\to X^{[2]}$
the natural morphisms, both defined over
![]() $\mathbb {R}$
. For any class
$\mathbb {R}$
. For any class
![]() $\gamma \neq [X]\in H^*(X, \mathbb {F}_2)$
, we first remark that
$\gamma \neq [X]\in H^*(X, \mathbb {F}_2)$
, we first remark that
Since
![]() $g_*\tau ^*(\gamma \otimes [X])\in H^*(X^{[2]}, \mathbb {F}_2)$
, which is the image of some
$g_*\tau ^*(\gamma \otimes [X])\in H^*(X^{[2]}, \mathbb {F}_2)$
, which is the image of some
![]() $\alpha \in H^*_G(X^{[2]}, \mathbb {F}_2)$
by the maximality assumption, we obtain that
$\alpha \in H^*_G(X^{[2]}, \mathbb {F}_2)$
by the maximality assumption, we obtain that
Taking any real point
![]() $p\in X(\mathbb {R})$
, define the
$p\in X(\mathbb {R})$
, define the
![]() $\mathbb {R}$
-morphism
$\mathbb {R}$
-morphism
![]() $i_p\colon X\to X\times X$
sending
$i_p\colon X\to X\times X$
sending
![]() $x$
to
$x$
to
![]() $(x, p)$
. It follows that
$(x, p)$
. It follows that
![]() $i_p^*(\gamma \otimes [X]+[X]\otimes \gamma )=\gamma$
is in the image of
$i_p^*(\gamma \otimes [X]+[X]\otimes \gamma )=\gamma$
is in the image of
![]() $H^*_G(X, \mathbb {F}_2)\to H^*(X, \mathbb {F}_2)$
. Therefore,
$H^*_G(X, \mathbb {F}_2)\to H^*(X, \mathbb {F}_2)$
. Therefore,
![]() $X$
is maximal by Proposition 2.3. (The maximality of
$X$
is maximal by Proposition 2.3. (The maximality of
![]() $X$
in the surface case is also shown by Kharlamov and Răsdeaconu in [Reference Kharlamov and RăsdeaconuKR23, Theorem 1.1] with a different argument and without the assumption
$X$
in the surface case is also shown by Kharlamov and Răsdeaconu in [Reference Kharlamov and RăsdeaconuKR23, Theorem 1.1] with a different argument and without the assumption
![]() $X(\mathbb {R})\neq \emptyset$
.)
$X(\mathbb {R})\neq \emptyset$
.)
Using (i),
![]() $X^{[1,2]}$
is maximal as well.
$X^{[1,2]}$
is maximal as well.
For
![]() $X^{[2,3]}$
, we first note that the universal subscheme in
$X^{[2,3]}$
, we first note that the universal subscheme in
![]() $X\times X^{[2]}$
is canonically identified with the nested Hilbert scheme
$X\times X^{[2]}$
is canonically identified with the nested Hilbert scheme
![]() $X^{[1,2]}$
, which is in turn isomorphic to
$X^{[1,2]}$
, which is in turn isomorphic to
![]() $\textrm {Bl}_{\Delta }(X\times X)$
as mentioned above. It is known that
$\textrm {Bl}_{\Delta }(X\times X)$
as mentioned above. It is known that
![]() $X^{[2,3]}$
is isomorphic to the blow-up of
$X^{[2,3]}$
is isomorphic to the blow-up of
![]() $X\times X^{[2]}$
along its universal subscheme. Hence
$X\times X^{[2]}$
along its universal subscheme. Hence
All the involved embeddings are real morphisms between smooth real varieties. Therefore, we can conclude the maximality of
![]() $X^{[2,3]}$
by invoking Lemma 3.1 and Proposition 3.5 together with the maximalities of
$X^{[2,3]}$
by invoking Lemma 3.1 and Proposition 3.5 together with the maximalities of
![]() $X$
,
$X$
,
![]() $X^{[2]}$
and
$X^{[2]}$
and
![]() $X^{[1,2]}$
.
$X^{[1,2]}$
.
Finally, for
![]() $X^{[3]}$
, note that there is a natural surjection
$X^{[3]}$
, note that there is a natural surjection
![]() $\pi \colon X^{[2,3]}\to X^{[3]}$
by forgetting the length 2 subscheme. It is easy to see that
$\pi \colon X^{[2,3]}\to X^{[3]}$
by forgetting the length 2 subscheme. It is easy to see that
![]() $\pi$
is generically finite of degree
$\pi$
is generically finite of degree
![]() $3$
(an odd number). Proposition 3.8 allows us to deduce the maximality of
$3$
(an odd number). Proposition 3.8 allows us to deduce the maximality of
![]() $X^{[3]}$
from that of
$X^{[3]}$
from that of
![]() $X^{[2,3]}$
.
$X^{[2,3]}$
.
Remark 7.4 (Loss of maximality in Hilbert squares). It is quite surprising that Kharlamov and Răsdeaconu [Reference Kharlamov and RăsdeaconuKR23] recently discovered the existence of maximal real surfaces with non-maximal Hilbert squares. In fact, they showed in [Reference Kharlamov and RăsdeaconuKR23, Theorem 1.2] that, for a real surface
![]() $X$
with
$X$
with
![]() $H^1(X, \mathbb {F}_2)=0$
, its Hilbert square
$H^1(X, \mathbb {F}_2)=0$
, its Hilbert square
![]() $X^{[2]}$
is maximal if and only if
$X^{[2]}$
is maximal if and only if
![]() $X(\mathbb {R})$
is connected. This finding led to the discovery of many examples of maximal surfaces with non-maximal Hilbert square, such as K3 surfaces. We will provide in Theorem 11.12 a higher-dimensional counter-example: the Hilbert square of a maximal real cubic 4-fold is never maximal.
$X(\mathbb {R})$
is connected. This finding led to the discovery of many examples of maximal surfaces with non-maximal Hilbert square, such as K3 surfaces. We will provide in Theorem 11.12 a higher-dimensional counter-example: the Hilbert square of a maximal real cubic 4-fold is never maximal.
Although taking the Hilbert square fails to preserve maximality in general, we provide an interesting example where Theorem7.3 can be applied. More examples in the surface case can be found in Section 8.
Theorem 7.5 (Cubic 3-folds). Let
![]() $X$
be a smooth real cubic 3-fold. If
$X$
be a smooth real cubic 3-fold. If
![]() $X$
is maximal, then
$X$
is maximal, then
![]() $X^{[2]}$
,
$X^{[2]}$
,
![]() $X^{[3]}$
,
$X^{[3]}$
,
![]() $X^{[1,2]}$
and
$X^{[1,2]}$
and
![]() $X^{[2,3]}$
are all maximal.
$X^{[2,3]}$
are all maximal.
Proof.
By Krasnov [Reference KrasnovKra05], the maximality of
![]() $X$
implies that its Fano surface of lines
$X$
implies that its Fano surface of lines
![]() $F:=F(X)$
is also maximal (see Proposition 3.14). Applying the realization functors
$F:=F(X)$
is also maximal (see Proposition 3.14). Applying the realization functors
![]() $H^*(-, \mathbb {F}_2)$
and
$H^*(-, \mathbb {F}_2)$
and
![]() $H^*(-(\mathbb {R}), \mathbb {F}_2)$
to the motivic Galkin–Shinder relation [Reference Galkin and ShinderGS14] established in [Reference Belmans, Fu and RaedscheldersBFR22, Corollary 18], we obtain the following relations between the total
$H^*(-(\mathbb {R}), \mathbb {F}_2)$
to the motivic Galkin–Shinder relation [Reference Galkin and ShinderGS14] established in [Reference Belmans, Fu and RaedscheldersBFR22, Corollary 18], we obtain the following relations between the total
![]() $\mathbb {F}_2$
-Betti numbers of
$\mathbb {F}_2$
-Betti numbers of
![]() $X$
,
$X$
,
![]() $F$
and
$F$
and
![]() $X^{[2]}$
:
$X^{[2]}$
:
 \begin{align*} b_*(F, \mathbb {F}_2)+4 b_*(X, \mathbb {F}_2)&=b_*(X^{[2]}, \mathbb {F}_2)\\ b_*(F(\mathbb {R}), \mathbb {F}_2)+4 b_*(X(\mathbb {R}), \mathbb {F}_2)&=b_*(X^{[2]}(\mathbb {R}), \mathbb {F}_2). \end{align*}
\begin{align*} b_*(F, \mathbb {F}_2)+4 b_*(X, \mathbb {F}_2)&=b_*(X^{[2]}, \mathbb {F}_2)\\ b_*(F(\mathbb {R}), \mathbb {F}_2)+4 b_*(X(\mathbb {R}), \mathbb {F}_2)&=b_*(X^{[2]}(\mathbb {R}), \mathbb {F}_2). \end{align*}
Therefore,
![]() $X^{[2]}$
is also maximal. We can conclude by applying Theorem7.3.
$X^{[2]}$
is also maximal. We can conclude by applying Theorem7.3.
8. Punctual Hilbert schemes of surfaces
As discussed in the previous section, for a smooth complex surface
![]() $S$
, the punctual Hilbert scheme/Douady space
$S$
, the punctual Hilbert scheme/Douady space
![]() $S^{[n]}$
is smooth for any
$S^{[n]}$
is smooth for any
![]() $n\geqslant 1$
[Reference FogartyFog68]. Moreover, a real structure on
$n\geqslant 1$
[Reference FogartyFog68]. Moreover, a real structure on
![]() $S$
naturally induces a real structure on
$S$
naturally induces a real structure on
![]() $S^{[n]}$
. This section aims to prove the maximality of Hilbert powers of certain maximal
$S^{[n]}$
. This section aims to prove the maximality of Hilbert powers of certain maximal
![]() $\mathbb {R}$
-surfaces:
$\mathbb {R}$
-surfaces:
Theorem 8.1.
Let
![]() $(S, \sigma )$
be a maximal smooth projective real surface with
$(S, \sigma )$
be a maximal smooth projective real surface with
![]() $H^1(S, \mathbb {F}_2)=0$
. If
$H^1(S, \mathbb {F}_2)=0$
. If
![]() $S(\mathbb {R})$
is connected, then
$S(\mathbb {R})$
is connected, then
![]() $S^{[n]}$
is maximal for any
$S^{[n]}$
is maximal for any
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
Remark 8.2. The case of
![]() $n=2$
in Theorem 8.1 gives a different proof of the ‘if’ part of Kharlamov and Răsdeaconu’s result [Reference Kharlamov and RăsdeaconuKR23, Theorem 1.2]. It is worth noting some details about the conditions in Theorem 8.1.
$n=2$
in Theorem 8.1 gives a different proof of the ‘if’ part of Kharlamov and Răsdeaconu’s result [Reference Kharlamov and RăsdeaconuKR23, Theorem 1.2]. It is worth noting some details about the conditions in Theorem 8.1.
-
– The condition on the connectedness of
 $S(\mathbb {R})$
can be equivalently replaced by
$S(\mathbb {R})$
can be equivalently replaced by
 $\textrm {rk} H^2(S, \mathbb {Z})^{\sigma }=0$
, or by
$\textrm {rk} H^2(S, \mathbb {Z})^{\sigma }=0$
, or by
 $c_1$
-maximality (Definition 4.2), as shown in Proposition 4.4.
$c_1$
-maximality (Definition 4.2), as shown in Proposition 4.4. -
– By Poincaré duality and the universal coefficient theorem, the condition
 $H^1(S, \mathbb {F}_2)=0$
is equivalent to
$H^1(S, \mathbb {F}_2)=0$
is equivalent to
 $b_{\operatorname {odd}}(S)=0$
and
$b_{\operatorname {odd}}(S)=0$
and
 $H^*(S, \mathbb {Z})$
has no 2-torsion. By Göttsche [Reference GöttscheG90] and Totaro [Reference TotaroTot20, Theorem 3.1], this condition implies that, for any
$H^*(S, \mathbb {Z})$
has no 2-torsion. By Göttsche [Reference GöttscheG90] and Totaro [Reference TotaroTot20, Theorem 3.1], this condition implies that, for any
 $n\geqslant 1$
, the odd Betti numbers of
$n\geqslant 1$
, the odd Betti numbers of
 $S^{[n]}$
vanish and the integral cohomology ring of
$S^{[n]}$
vanish and the integral cohomology ring of
 $S^{[n]}$
is 2-torsion-free.
$S^{[n]}$
is 2-torsion-free. -
– All the conditions in Theorem 8.1 are invariant under blow-ups at real points.
Remark 8.3 (Nested Hilbert schemes). By Theorem 7.3, for any maximal real surface
![]() $S$
satisfying the conditions in Theorem 8.1, the nested Hilbert schemes
$S$
satisfying the conditions in Theorem 8.1, the nested Hilbert schemes
![]() $S^{[1,2]}$
and
$S^{[1,2]}$
and
![]() $S^{[2,3]}$
are also maximal. However, by Cheah [Reference CheahChe98], in dimension 2, all the nested Hilbert schemes
$S^{[2,3]}$
are also maximal. However, by Cheah [Reference CheahChe98], in dimension 2, all the nested Hilbert schemes
![]() $S^{[n,n+1]}$
are smooth. This raises the interesting question of whether
$S^{[n,n+1]}$
are smooth. This raises the interesting question of whether
![]() $S^{[n, n+1]}$
is maximal for any
$S^{[n, n+1]}$
is maximal for any
![]() $n$
in this case.
$n$
in this case.
Our strategy for proving Theorem8.1 is similar to that of Theorem5.3. We will rely on the following result of Li and Qin [Reference Li and QinLQ08, Theorem 1.2] (based on [Reference Li, Qin and WangLQW02b, Reference Li, Qin and WangLQW02a, Reference Li, Qin and WangLQW03, Reference Qin and WangQW05]) on the generators of the cohomology ring of
![]() $S^{[n]}$
, which can be viewed as the analogue of Atiyah and Bott’s Theorem5.1.
$S^{[n]}$
, which can be viewed as the analogue of Atiyah and Bott’s Theorem5.1.
Theorem 8.4 (Li–Qin). Let
![]() $S$
be a smooth projective complex surface with
$S$
be a smooth projective complex surface with
![]() $b_1(S)=0$
, and
$b_1(S)=0$
, and
![]() $n$
a positive integer. Then
$n$
a positive integer. Then
![]() $H^*(S^{[n]}, \mathbb {Z})/\textrm {Tors}$
is generated by the following three types of elements:
$H^*(S^{[n]}, \mathbb {Z})/\textrm {Tors}$
is generated by the following three types of elements:
-
(i) for
 $1\leqslant r\leqslant n$
, the Chern class
$1\leqslant r\leqslant n$
, the Chern class
 $c_r(\mathcal {O}_S^{[n]})\in H^{2r}(S^{[n]}, \mathbb {Z})$
, where
$c_r(\mathcal {O}_S^{[n]})\in H^{2r}(S^{[n]}, \mathbb {Z})$
, where
 $\mathcal {O}_S^{[n]}$
is the tautological rank-
$\mathcal {O}_S^{[n]}$
is the tautological rank-
 $n$
bundle defined as
$n$
bundle defined as
 $p_*(\mathcal {O}_{\mathcal {Z}_n})$
where
$p_*(\mathcal {O}_{\mathcal {Z}_n})$
where
 $p\colon S^{[n]}\times S\to S^{[n]}$
is the projection and
$p\colon S^{[n]}\times S\to S^{[n]}$
is the projection and
 $\mathcal {Z}_n\subset S^{[n]}\times S$
is the universal subscheme;
$\mathcal {Z}_n\subset S^{[n]}\times S$
is the universal subscheme;
-
(ii) for
 $1\leqslant r\leqslant n$
, and
$1\leqslant r\leqslant n$
, and
 $\alpha \in H^2(S, \mathbb {Z})/\textrm {Tors}$
, the class
$\alpha \in H^2(S, \mathbb {Z})/\textrm {Tors}$
, the class
 $\unicode {x1D7D9}_{-(n-r)}\mathfrak {m}_{(1^r), \alpha }|0\rangle$
;
$\unicode {x1D7D9}_{-(n-r)}\mathfrak {m}_{(1^r), \alpha }|0\rangle$
; -
(iii) for
 $1\leqslant r\leqslant n$
, the class
$1\leqslant r\leqslant n$
, the class
 $\unicode {x1D7D9}_{-(n-r)}\mathfrak {p}_{-r}(\textrm {pt})|0\rangle$
, where
$\unicode {x1D7D9}_{-(n-r)}\mathfrak {p}_{-r}(\textrm {pt})|0\rangle$
, where
 $\textrm {pt}\in H^4(S, \mathbb {Z})$
denotes the class of a point.
$\textrm {pt}\in H^4(S, \mathbb {Z})$
denotes the class of a point.
Here
![]() $|0\rangle$
denotes the positive generator of
$|0\rangle$
denotes the positive generator of
![]() $H^0(S^{[0]}, \mathbb {Z})$
, the operator
$H^0(S^{[0]}, \mathbb {Z})$
, the operator
![]() $\mathfrak {p}$
is Nakajima’s operator [Reference NakajimaNak99] and the operators
$\mathfrak {p}$
is Nakajima’s operator [Reference NakajimaNak99] and the operators
![]() $\unicode {x1D7D9}$
and
$\unicode {x1D7D9}$
and
![]() $\mathfrak {m}$
are defined in [Reference Li, Qin and WangLQW03, Reference Qin and WangQW05, Reference Li and QinLQ08]; see the explanation in the remark below.
$\mathfrak {m}$
are defined in [Reference Li, Qin and WangLQW03, Reference Qin and WangQW05, Reference Li and QinLQ08]; see the explanation in the remark below.
Remark 8.5 (Operators). Let us give some more details on the operators
![]() $\mathfrak {p}$
,
$\mathfrak {p}$
,
![]() $\unicode {x1D7D9}$
and
$\unicode {x1D7D9}$
and
![]() $\mathfrak {m}$
. In the discussion below, the coefficients of the cohomology can be chosen arbitrarily (e.g.
$\mathfrak {m}$
. In the discussion below, the coefficients of the cohomology can be chosen arbitrarily (e.g.
![]() $\mathbb {Z}$
), and are omitted.
$\mathbb {Z}$
), and are omitted.
-
(i) For any
 $r\geqslant 0$
and any
$r\geqslant 0$
and any
 $\alpha \in H^*(S)$
, the (creation) Nakajima operator
$\alpha \in H^*(S)$
, the (creation) Nakajima operator
 $\mathfrak {p}_{-r}(\alpha )$
sends, for any
$\mathfrak {p}_{-r}(\alpha )$
sends, for any
 $j\geqslant 0$
, an element
$j\geqslant 0$
, an element
 $\beta \in H^*(S^{[j]})$
to the class
$\beta \in H^*(S^{[j]})$
to the class
 $q_*(p^*(\beta )\smile \rho ^*(\alpha )\smile [Q_{j+r, j}])\in H^*(S^{[j+r]})$
, where
$q_*(p^*(\beta )\smile \rho ^*(\alpha )\smile [Q_{j+r, j}])\in H^*(S^{[j+r]})$
, where
 $Q_{j+r, j}:=\{(Z, x, Z^{\prime})\in S^{[j]}\times S\times S^{[j+r]}\ |\ \operatorname {supp}(I_Z/I_{Z^{\prime}})=\{x\}\}$
, and
$Q_{j+r, j}:=\{(Z, x, Z^{\prime})\in S^{[j]}\times S\times S^{[j+r]}\ |\ \operatorname {supp}(I_Z/I_{Z^{\prime}})=\{x\}\}$
, and
 $p, \rho\ \text{and}\ q$
are the projections from
$p, \rho\ \text{and}\ q$
are the projections from
 $S^{[j]}\times S\times S^{[j+r]}$
to
$S^{[j]}\times S\times S^{[j+r]}$
to
 $S^{[j]}$
,
$S^{[j]}$
,
 $S$
and
$S$
and
 $S^{[j+r]}$
, respectively. In particular, taking
$S^{[j+r]}$
, respectively. In particular, taking
 $j=0$
, then
$j=0$
, then
 $\mathfrak {p}_{-r}(\alpha )|0\rangle$
is the image of
$\mathfrak {p}_{-r}(\alpha )|0\rangle$
is the image of
 $\alpha$
via the correspondence
$\alpha$
via the correspondence
 $[\Gamma _r]_*\colon H^*(S)\to H^*(S^{[r]})$
, where
$[\Gamma _r]_*\colon H^*(S)\to H^*(S^{[r]})$
, where
 $\Gamma _r:=\{(x, Z)\in S\times S^{[r]}\ |\ \operatorname {supp}(Z)=\{x\}\}$
.
$\Gamma _r:=\{(x, Z)\in S\times S^{[r]}\ |\ \operatorname {supp}(Z)=\{x\}\}$
. -
(ii) For any
 $r\geqslant 0$
, the operator
$r\geqslant 0$
, the operator
 $\unicode {x1D7D9}_{-r}$
is defined in [Reference Li, Qin and WangLQW03, Definition 4.1] and [Reference Li and QinLQ08, (2.7)] as
$\unicode {x1D7D9}_{-r}$
is defined in [Reference Li, Qin and WangLQW03, Definition 4.1] and [Reference Li and QinLQ08, (2.7)] as
 $\unicode {x1D7D9}_{-r}:=\frac {1}{r!}\mathfrak {p}_{-1}(1_S)^r$
. Despite of the apparent denominator, in [Reference Qin and WangQW05, Lemma 3.3] it is proved that
$\unicode {x1D7D9}_{-r}:=\frac {1}{r!}\mathfrak {p}_{-1}(1_S)^r$
. Despite of the apparent denominator, in [Reference Qin and WangQW05, Lemma 3.3] it is proved that
 $\unicode {x1D7D9}_{-r}$
is an integral operator. Indeed, it can be equivalently defined as follows: for any
$\unicode {x1D7D9}_{-r}$
is an integral operator. Indeed, it can be equivalently defined as follows: for any
 $j\geqslant 0$
, the operator
$j\geqslant 0$
, the operator
 $\unicode {x1D7D9}_{-r}: H^*(S^{[j]})\to H^*(S^{[j+r]})$
is the correspondence
$\unicode {x1D7D9}_{-r}: H^*(S^{[j]})\to H^*(S^{[j+r]})$
is the correspondence
 $[S^{[j, j+r]}]_*$
, where
$[S^{[j, j+r]}]_*$
, where
 $S^{[j, j+r]}:=\{ (Z, Z^{\prime}) \in S^{[j]}\times S^{[j+r]}\ |\ Z\subset Z^{\prime}\}$
is the nested Hilbert scheme.
$S^{[j, j+r]}:=\{ (Z, Z^{\prime}) \in S^{[j]}\times S^{[j+r]}\ |\ Z\subset Z^{\prime}\}$
is the nested Hilbert scheme. -
(iii) The operator
 $\mathfrak {m}$
is defined in [Reference Qin and WangQW05, §4.2] and in [Reference Li and QinLQ08, Definition 3.3]. The precise definition is somewhat involved. Let us only mention here that when
$\mathfrak {m}$
is defined in [Reference Qin and WangQW05, §4.2] and in [Reference Li and QinLQ08, Definition 3.3]. The precise definition is somewhat involved. Let us only mention here that when
 $\alpha =[C]$
for a smooth irreducible curve
$\alpha =[C]$
for a smooth irreducible curve
 $C$
in
$C$
in
 $S$
, then, for any partition
$S$
, then, for any partition
 $\lambda =(\lambda _1\geqslant \cdots \geqslant \lambda _N)$
of
$\lambda =(\lambda _1\geqslant \cdots \geqslant \lambda _N)$
of
 $n$
, we have
$n$
, we have
 $\mathfrak {m}_{\lambda, C}|0\rangle = [L^\lambda C]$
, where
$\mathfrak {m}_{\lambda, C}|0\rangle = [L^\lambda C]$
, where
 $L^\lambda C$
is the closure in
$L^\lambda C$
is the closure in
 $S^{[n]}$
of
$S^{[n]}$
of
 $\{\lambda _1x_1+\cdots +\lambda _Nx_N | x_i \in S \text { distinct}\}.$
An interpretation which works for
$\{\lambda _1x_1+\cdots +\lambda _Nx_N | x_i \in S \text { distinct}\}.$
An interpretation which works for
 $\lambda =(1^n)$
and for any class
$\lambda =(1^n)$
and for any class
 $\alpha$
will be given and used in the proof of Theorem 8.1 below.
$\alpha$
will be given and used in the proof of Theorem 8.1 below.
Proof of Theorem. By Remark 8.2, the condition
![]() $H^1(S, \mathbb {F}_2)=0$
implies that
$H^1(S, \mathbb {F}_2)=0$
implies that
![]() $b_{\operatorname {odd}}(S^{[n]})=0$
and
$b_{\operatorname {odd}}(S^{[n]})=0$
and
![]() $H^*(S^{[n]}, \mathbb {Z})$
has no 2-torsion. By the universal coefficient theorem, the cohomology ring
$H^*(S^{[n]}, \mathbb {Z})$
has no 2-torsion. By the universal coefficient theorem, the cohomology ring
![]() $H^*(S^{[n]}, \mathbb {F}_2)$
is generated by the same collection of generators in Theorem8.4 by passing to
$H^*(S^{[n]}, \mathbb {F}_2)$
is generated by the same collection of generators in Theorem8.4 by passing to
![]() $\mathbb {F}_2$
-coefficients. Like in Theorem5.3, we only need to show that all the generators are in the image of the restriction map
$\mathbb {F}_2$
-coefficients. Like in Theorem5.3, we only need to show that all the generators are in the image of the restriction map
![]() $H^*_G(S^{[n]}, \mathbb {F}_2)\to H^*(S^{[n]}, \mathbb {F}_2)$
.
$H^*_G(S^{[n]}, \mathbb {F}_2)\to H^*(S^{[n]}, \mathbb {F}_2)$
.
- For generators in (i), since the tautological vector bundle
![]() $\mathcal {O}_S^{[n]}$
is a holomorphic real vector bundle on
$\mathcal {O}_S^{[n]}$
is a holomorphic real vector bundle on
![]() $S^{[n]}$
by construction, it hence defines a class
$S^{[n]}$
by construction, it hence defines a class
![]() $[\mathcal {O}_S^{[n]}]\in \textrm {KR}^0(S^{[n]})$
. As
$[\mathcal {O}_S^{[n]}]\in \textrm {KR}^0(S^{[n]})$
. As
![]() $c^G_r(\mathcal {O}_S^{[n]})\in H^*_G(S^{[n]}, \mathbb {F}_2)$
is mapped to
$c^G_r(\mathcal {O}_S^{[n]})\in H^*_G(S^{[n]}, \mathbb {F}_2)$
is mapped to
![]() $c_r(\mathcal {O}_S^{[n]}) \in H^*(S^{[n]}, \mathbb {F}_2)$
, the latter is in the image of the restriction map.
$c_r(\mathcal {O}_S^{[n]}) \in H^*(S^{[n]}, \mathbb {F}_2)$
, the latter is in the image of the restriction map.
- For generators in (ii), given a class
![]() $\alpha \in H^2(S, \mathbb {F}_2)$
, by Proposition 4.4,
$\alpha \in H^2(S, \mathbb {F}_2)$
, by Proposition 4.4,
![]() $S$
is
$S$
is
![]() $c_1$
-maximal, i.e.
$c_1$
-maximal, i.e.
![]() $c_1\colon \textrm {KR}^0(S)\to H^2(S, \mathbb {F}_2)$
is surjective, and there exists an element
$c_1\colon \textrm {KR}^0(S)\to H^2(S, \mathbb {F}_2)$
is surjective, and there exists an element
![]() $L\in \textrm {KR}^0(S)$
such that
$L\in \textrm {KR}^0(S)$
such that
![]() $c_1(L)=\alpha$
. Up to replacing
$c_1(L)=\alpha$
. Up to replacing
![]() $L$
by its determinant, one can in fact assume that
$L$
by its determinant, one can in fact assume that
![]() $L$
is a real vector bundle of rank 1.
$L$
is a real vector bundle of rank 1.
We denote by
![]() $\widetilde {\alpha }:=c_1^G(L)\in H^2_G(S, \mathbb {F}_2)$
the equivariant first Chern class of
$\widetilde {\alpha }:=c_1^G(L)\in H^2_G(S, \mathbb {F}_2)$
the equivariant first Chern class of
![]() $L$
. Clearly,
$L$
. Clearly,
![]() $\widetilde {\alpha }$
is mapped to
$\widetilde {\alpha }$
is mapped to
![]() $\alpha$
under the restriction map. Let
$\alpha$
under the restriction map. Let
![]() $\mathcal {Z}_n\subset S^{[r]}\times S$
be the universal subscheme. Let
$\mathcal {Z}_n\subset S^{[r]}\times S$
be the universal subscheme. Let
![]() $p_1\ \text{and}\ p_2$
be the two natural projections from
$p_1\ \text{and}\ p_2$
be the two natural projections from
![]() $\mathcal {Z}_r$
to
$\mathcal {Z}_r$
to
![]() $S^{[r]}$
and
$S^{[r]}$
and
![]() $S$
, which are real morphisms since
$S$
, which are real morphisms since
![]() $\mathcal {Z}_n$
is a subscheme defined over
$\mathcal {Z}_n$
is a subscheme defined over
![]() $\mathbb {R}$
. We thus obtain an element
$\mathbb {R}$
. We thus obtain an element
![]() $p_{1,!}(p_2^*(L))\in \textrm {KR}^0(S^{[n]})$
. By the proof of [Reference Li and QinLQ08, Lemma 3.5], we have the following equality (which holds integrally):
$p_{1,!}(p_2^*(L))\in \textrm {KR}^0(S^{[n]})$
. By the proof of [Reference Li and QinLQ08, Lemma 3.5], we have the following equality (which holds integrally):
Therefore,
![]() $c^G_r(p_{1,!}(p_2^*(L)))\in H_G^*(S^{[r]}, \mathbb {F}_2)$
is mapped to
$c^G_r(p_{1,!}(p_2^*(L)))\in H_G^*(S^{[r]}, \mathbb {F}_2)$
is mapped to
![]() $\mathfrak {m}_{(1^r), \alpha }$
via the restriction map.
$\mathfrak {m}_{(1^r), \alpha }$
via the restriction map.
Now consider the commutative diagram

where the vertical arrows are restriction maps, and the horizontal maps are given by the correspondences induced by the nested Hilbert scheme
![]() $S^{[r,n]}:=\{(Z, Z^{\prime})\in S^{[r]}\times S^{[n]}\ |\ Z \subset Z^{\prime}\}$
, viewed as algebraic cycles (defined over
$S^{[r,n]}:=\{(Z, Z^{\prime})\in S^{[r]}\times S^{[n]}\ |\ Z \subset Z^{\prime}\}$
, viewed as algebraic cycles (defined over
![]() $\mathbb {R})$
. By Remark 8.5, the bottom arrow sends
$\mathbb {R})$
. By Remark 8.5, the bottom arrow sends
![]() $\mathfrak {m}_{(1^r), \alpha }$
to
$\mathfrak {m}_{(1^r), \alpha }$
to
![]() $\unicode {x1D7D9}_{-(n-r)}\mathfrak {m}_{(1^r), \alpha }$
. Since we just proved that
$\unicode {x1D7D9}_{-(n-r)}\mathfrak {m}_{(1^r), \alpha }$
. Since we just proved that
![]() $\mathfrak {m}_{(1^r), \alpha }$
is in the image of the left vertical arrow, we conclude by the commutativity of the diagram that
$\mathfrak {m}_{(1^r), \alpha }$
is in the image of the left vertical arrow, we conclude by the commutativity of the diagram that
![]() $\unicode {x1D7D9}_{-(n-r)}\mathfrak {m}_{(1^r), \alpha }$
is in the image of the right vertical arrow.
$\unicode {x1D7D9}_{-(n-r)}\mathfrak {m}_{(1^r), \alpha }$
is in the image of the right vertical arrow.
- For generators in (iii), by definition,
![]() $\unicode {x1D7D9}_{-(n-r)}\mathfrak {p}_{-r}(\textrm {pt})|0\rangle$
is the image of the class
$\unicode {x1D7D9}_{-(n-r)}\mathfrak {p}_{-r}(\textrm {pt})|0\rangle$
is the image of the class
![]() $[\textrm {pt}]\in H^4(S)$
under the following composition of correspondences:
$[\textrm {pt}]\in H^4(S)$
under the following composition of correspondences:
where
![]() $\Gamma _r:=\{(x, Z)\in S\times S^{[r]}\ |\ \operatorname {supp}(Z)=\{x\}\}$
and
$\Gamma _r:=\{(x, Z)\in S\times S^{[r]}\ |\ \operatorname {supp}(Z)=\{x\}\}$
and
![]() $S^{[r,n]}$
is as above, both viewed as algebraic cycles (see Remark 8.5). However,
$S^{[r,n]}$
is as above, both viewed as algebraic cycles (see Remark 8.5). However,
![]() $\Gamma _n$
and
$\Gamma _n$
and
![]() $S^{[r,n]}$
(although singular) are defined over
$S^{[r,n]}$
(although singular) are defined over
![]() $\mathbb {R}$
, so they induce equivariant correspondences; we have the commutative diagram
$\mathbb {R}$
, so they induce equivariant correspondences; we have the commutative diagram

where all the vertical arrows are restriction maps and the left one is surjective since
![]() $S$
is maximal (Lemma 4.3). Therefore,
$S$
is maximal (Lemma 4.3). Therefore,
![]() $\unicode {x1D7D9}_{-(n-r)}\mathfrak {p}_{-r}(\textrm {pt})|0\rangle =[S^{[r,n]}]_*\circ [\Gamma _r]_*([\textrm {pt}])$
is in the image of the restriction map.
$\unicode {x1D7D9}_{-(n-r)}\mathfrak {p}_{-r}(\textrm {pt})|0\rangle =[S^{[r,n]}]_*\circ [\Gamma _r]_*([\textrm {pt}])$
is in the image of the restriction map.
To summarize, all types of generators lie in the image of the restriction map
![]() $H^*_G(S^{[n]}, \mathbb {F}_2)\to H^*(S^{[n]}, \mathbb {F}_2)$
, and hence the latter is surjective, and
$H^*_G(S^{[n]}, \mathbb {F}_2)\to H^*(S^{[n]}, \mathbb {F}_2)$
, and hence the latter is surjective, and
![]() $S^{[n]}$
is maximal by Proposition 2.3.
$S^{[n]}$
is maximal by Proposition 2.3.
We provide two types of surfaces to which Theorem8.1 applies: rational surfaces and some surfaces of Kodaira dimension 1.
8.1 Example I: rational surfaces
The first type of examples includes
![]() $\mathbb {P}^2$
,
$\mathbb {P}^2$
,
![]() $\mathbb {P}^1\times \mathbb {P}^1$
and Hirzebruch surfaces, as well as blow-ups of these surfaces at real points.
$\mathbb {P}^1\times \mathbb {P}^1$
and Hirzebruch surfaces, as well as blow-ups of these surfaces at real points.
Corollary 8.6.
The punctual Hilbert schemes of a maximal
![]() $\mathbb {R}$
-rational real surface are maximal.
$\mathbb {R}$
-rational real surface are maximal.
Proof.
By Theorem8.1, we only need to verify that
![]() $H^1(S, \mathbb {F}_2)=0$
and that
$H^1(S, \mathbb {F}_2)=0$
and that
![]() $S(\mathbb {R})$
is connected (or, equivalently,
$S(\mathbb {R})$
is connected (or, equivalently,
![]() $c_1$
-maximal). The former is obvious for rational surfaces, and the latter follows from Lemmas 4.5 and 4.3.
$c_1$
-maximal). The former is obvious for rational surfaces, and the latter follows from Lemmas 4.5 and 4.3.
Remark 8.7 (Del Pezzo of degree 1). If we consider a more general class of surfaces, namely geometrically rational surfaces, which are real surface
![]() $S$
with
$S$
with
![]() $S_{\mathbb {C}}$
rational, there is another type of maximal minimal real surface, namely
$S_{\mathbb {C}}$
rational, there is another type of maximal minimal real surface, namely
![]() $\mathbb {B}_1$
, the real minimal del Pezzo surface of degree 1 whose real locus is
$\mathbb {B}_1$
, the real minimal del Pezzo surface of degree 1 whose real locus is
![]() $\mathbb {R}\mathbb {P}^2\coprod 4 \mathbb {S}^2$
; see [Reference KollárKol01, Reference RussoRus02]. By Proposition 4.4,
$\mathbb {R}\mathbb {P}^2\coprod 4 \mathbb {S}^2$
; see [Reference KollárKol01, Reference RussoRus02]. By Proposition 4.4,
![]() $\mathbb {B}_1$
is not
$\mathbb {B}_1$
is not
![]() $c_1$
-maximal (nor K-maximal). According to the result of Kharlamov and Răsdeaconu [Reference Kharlamov and RăsdeaconuKR23] mentioned in Remark 7.4, the Hilbert square of
$c_1$
-maximal (nor K-maximal). According to the result of Kharlamov and Răsdeaconu [Reference Kharlamov and RăsdeaconuKR23] mentioned in Remark 7.4, the Hilbert square of
![]() $\mathbb {B}_1$
is not maximal. Furthermore, note that
$\mathbb {B}_1$
is not maximal. Furthermore, note that
![]() $\mathbb {B}_1$
is not Hodge expressive in the sense of [Reference Brugallé and SchaffhauserBS22].
$\mathbb {B}_1$
is not Hodge expressive in the sense of [Reference Brugallé and SchaffhauserBS22].
8.2 Example II: generalized Dolgachev surfaces
Let
![]() $m\gt 1$
be an integer, and choose another auxiliary integer
$m\gt 1$
be an integer, and choose another auxiliary integer
![]() $0\lt k\lt m$
. Recall that, for a relatively minimal elliptic surface
$0\lt k\lt m$
. Recall that, for a relatively minimal elliptic surface
![]() $f\colon S\to C$
with a smooth fiber
$f\colon S\to C$
with a smooth fiber
![]() $S_c$
over a point
$S_c$
over a point
![]() $c\in C$
, a logarithmic transformation of order
$c\in C$
, a logarithmic transformation of order
![]() $m$
at
$m$
at
![]() $c$
produces another relatively minimal elliptic surface
$c$
produces another relatively minimal elliptic surface
![]() $f^{\prime}\colon S^{\prime}\to C$
with a multiple fiber
$f^{\prime}\colon S^{\prime}\to C$
with a multiple fiber
![]() $S^{\prime}_c$
of multiplicity
$S^{\prime}_c$
of multiplicity
![]() $m$
over
$m$
over
![]() $c$
, such that
$c$
, such that
![]() $S\backslash S_c$
is isomorphic to
$S\backslash S_c$
is isomorphic to
![]() $S^{\prime}\backslash S^{\prime}_c$
over
$S^{\prime}\backslash S^{\prime}_c$
over
![]() $C\backslash \{c\}$
. In fact, the logarithmic transformation can be performed more generally to replace a fiber of type
$C\backslash \{c\}$
. In fact, the logarithmic transformation can be performed more generally to replace a fiber of type
![]() $I_b$
in an elliptic fibration by a multiple fiber of type
$I_b$
in an elliptic fibration by a multiple fiber of type
![]() ${}_mI_b$
. We refer to [Reference Barth, Hulek, Peters and Van de VenBHPVdV04, Chapter V, §13] for more details.
${}_mI_b$
. We refer to [Reference Barth, Hulek, Peters and Van de VenBHPVdV04, Chapter V, §13] for more details.
Dolgachev [Reference DolgachevDol10] used logarithmic transformations to construct simply connected irrational elliptic surfaces of Kodaira dimension 1 with vanishing geometric genus. Although all homeomorphic to the blow-up of
![]() $\mathbb {P}^2$
at nine points [Reference FreedmanFre82], Donaldson [Reference DonaldsonDon87] and Okonek and Van de Ven [Reference Okonek and Van de VenOVdV86] showed that Dolgachev surfaces provide infinitely many distinct diffeomorphic types.
$\mathbb {P}^2$
at nine points [Reference FreedmanFre82], Donaldson [Reference DonaldsonDon87] and Okonek and Van de Ven [Reference Okonek and Van de VenOVdV86] showed that Dolgachev surfaces provide infinitely many distinct diffeomorphic types.
For our purpose, we follow Lübke and Okonek [Reference Lübke and OkonekLO87] to construct certain variants of Dolgachev surfaces and adapt them to real geometry. We consider two real smooth planar cubic curves intersecting at nine distinct real points in
![]() $\mathbb {P}^2(\mathbb {R})$
. Blowing up these nine points, we get an
$\mathbb {P}^2(\mathbb {R})$
. Blowing up these nine points, we get an
![]() $\mathbb {R}$
-rational surface
$\mathbb {R}$
-rational surface
![]() $S$
fibered in elliptic curves over
$S$
fibered in elliptic curves over
![]() $ \mathbb {P}^1$
. The morphism
$ \mathbb {P}^1$
. The morphism
is defined over
![]() $\mathbb {R}$
. For any odd integer
$\mathbb {R}$
. For any odd integer
![]() $m\gt 2$
and a generic pair of complex conjugate points
$m\gt 2$
and a generic pair of complex conjugate points
![]() $t, \bar {t} \in \mathbb {P}^1(\mathbb {C})\backslash \mathbb {P}^1(\mathbb {R})$
, performing the logarithmic transformations at
$t, \bar {t} \in \mathbb {P}^1(\mathbb {C})\backslash \mathbb {P}^1(\mathbb {R})$
, performing the logarithmic transformations at
![]() $t$
and
$t$
and
![]() $\bar {t}$
of the same order
$\bar {t}$
of the same order
![]() $m$
(and with the same auxiliary choice of
$m$
(and with the same auxiliary choice of
![]() $k$
) produces another elliptic surface
$k$
) produces another elliptic surface
![]() $S_{m,m}\to \mathbb {P}^1$
which is isomorphic to
$S_{m,m}\to \mathbb {P}^1$
which is isomorphic to
![]() $S$
over
$S$
over
![]() $\mathbb {P}^1\backslash \{t, \bar {t}\}$
. The real structure on
$\mathbb {P}^1\backslash \{t, \bar {t}\}$
. The real structure on
![]() $S$
gives rise to a real structure on
$S$
gives rise to a real structure on
![]() $S_{m,m}$
.
$S_{m,m}$
.
Lemma 8.8.
The real locus of
![]() $S_{m,m}$
is
$S_{m,m}$
is
with
![]() $\mathbb {F}_2$
-Betti numbers 1, 10, 1.
$\mathbb {F}_2$
-Betti numbers 1, 10, 1.
The
![]() $\mathbb {F}_2$
-Betti numbers of
$\mathbb {F}_2$
-Betti numbers of
![]() $S_{m,m}$
are 1, 0, 10, 0, 1. In particular,
$S_{m,m}$
are 1, 0, 10, 0, 1. In particular,
![]() $S_{m, m}$
is a maximal real surface.
$S_{m, m}$
is a maximal real surface.
Proof.
Since the logarithmic transformation along two conjugate complex points does not change the real locus,
![]() $S_{m,m}(\mathbb {R})$
is the same as the real locus of the blow-up of
$S_{m,m}(\mathbb {R})$
is the same as the real locus of the blow-up of
![]() $\mathbb {P}^2$
at nine real points. As blowing up at a real point modifies the real locus by taking a connected sum with a copy of
$\mathbb {P}^2$
at nine real points. As blowing up at a real point modifies the real locus by taking a connected sum with a copy of
![]() $\mathbb {R}\mathbb {P}^2$
, the formula of
$\mathbb {R}\mathbb {P}^2$
, the formula of
![]() $S_{m,m}(\mathbb {R})$
follows. Its
$S_{m,m}(\mathbb {R})$
follows. Its
![]() $\mathbb {F}_2$
-Betti numbers can be easily computed.
$\mathbb {F}_2$
-Betti numbers can be easily computed.
Contrary to the simple connectedness of the classical Dolgachev surfaces, we know that
![]() $\pi _1(S_{m,m})\cong \mathbb {Z}/m\mathbb {Z}$
(see [Reference DolgachevDol10] or [Reference Lübke and OkonekLO87]). Since
$\pi _1(S_{m,m})\cong \mathbb {Z}/m\mathbb {Z}$
(see [Reference DolgachevDol10] or [Reference Lübke and OkonekLO87]). Since
![]() $m$
is odd,
$m$
is odd,
![]() $H^1(S_{m,m}, \mathbb {F}_2)=0$
. The Euler characteristic is not changed by logarithmic transformations (and hence is equal to
$H^1(S_{m,m}, \mathbb {F}_2)=0$
. The Euler characteristic is not changed by logarithmic transformations (and hence is equal to
![]() $\chi _{\mathrm {top}}(\textrm {Bl}_{9}\mathbb {P}^2)=12$
), and therefore the
$\chi _{\mathrm {top}}(\textrm {Bl}_{9}\mathbb {P}^2)=12$
), and therefore the
![]() $\mathbb {F}_2$
-Betti numbers of
$\mathbb {F}_2$
-Betti numbers of
![]() $S_{m,m}$
can be determined.
$S_{m,m}$
can be determined.
Corollary 8.9 (Generalized Dolgachev surface). The punctual Hilbert schemes of the real surfaces
![]() $S_{m,m}$
constructed above are maximal.
$S_{m,m}$
constructed above are maximal.
Proof.
By Lemma 8.8, the surface
![]() $S_{m,m}$
satisfies all the conditions in Theorem8.1, which implies that its punctual Hilbert schemes are maximal.
$S_{m,m}$
satisfies all the conditions in Theorem8.1, which implies that its punctual Hilbert schemes are maximal.
Remark 8.10. The surfaces
![]() $S_{m,m}$
provide infinitely many new examples as they have Kodaira dimension 1 (see [Reference Lübke and OkonekLO87, p. 219]) and, by [Reference Lübke and OkonekLO87, p. 220, Corollary],
$S_{m,m}$
provide infinitely many new examples as they have Kodaira dimension 1 (see [Reference Lübke and OkonekLO87, p. 219]) and, by [Reference Lübke and OkonekLO87, p. 220, Corollary],
![]() $\{S_{m,m}\}_m$
contains infinitely many diffeomorphic types.
$\{S_{m,m}\}_m$
contains infinitely many diffeomorphic types.
9. Moduli spaces of sheaves on the projective plane
Given integers
![]() $r\gt 0, c_1, c_2$
, let
$r\gt 0, c_1, c_2$
, let
![]() $M:=M(r, c_1, c_2)$
be the moduli space of stable sheaves of rank
$M:=M(r, c_1, c_2)$
be the moduli space of stable sheaves of rank
![]() $r$
with first and second Chern classes
$r$
with first and second Chern classes
![]() $c_1$
and
$c_1$
and
![]() $c_2$
on the complex projective plane
$c_2$
on the complex projective plane
![]() $\mathbb {P}^2_{\mathbb {C}}$
. Assume that
$\mathbb {P}^2_{\mathbb {C}}$
. Assume that
Then
![]() $M$
is a smooth projective fine moduli space.
$M$
is a smooth projective fine moduli space.
We equip
![]() $\mathbb {P}^2_{\mathbb {C}}$
with its standard real structure
$\mathbb {P}^2_{\mathbb {C}}$
with its standard real structure
![]() $\sigma$
. We claim that this induces a natural real structure
$\sigma$
. We claim that this induces a natural real structure
![]() $\sigma _M$
on
$\sigma _M$
on
![]() $M$
:
$M$
:
Indeed,
![]() $\sigma _M$
is clearly anti-holomorphic of order 2, and we only need to show that the Chern classes of
$\sigma _M$
is clearly anti-holomorphic of order 2, and we only need to show that the Chern classes of
![]() $\overline {\sigma ^*(E)}$
and
$\overline {\sigma ^*(E)}$
and
![]() $E$
are the same: first, it is easy to see that
$E$
are the same: first, it is easy to see that
![]() $\sigma ^*$
acts on cohomology as
$\sigma ^*$
acts on cohomology as
![]() $\textrm {id}$
on
$\textrm {id}$
on
![]() $H^0(\mathbb {P}^2_{\mathbb {C}}, \mathbb {Z})\oplus H^4(\mathbb {P}^2_{\mathbb {C}}, \mathbb {Z})$
and as
$H^0(\mathbb {P}^2_{\mathbb {C}}, \mathbb {Z})\oplus H^4(\mathbb {P}^2_{\mathbb {C}}, \mathbb {Z})$
and as
![]() $-\textrm {id}$
on
$-\textrm {id}$
on
![]() $H^2(\mathbb {P}^2_{\mathbb {C}}, \mathbb {Z})$
(because complex conjugate changes of orientation on
$H^2(\mathbb {P}^2_{\mathbb {C}}, \mathbb {Z})$
(because complex conjugate changes of orientation on
![]() $\mathbb {C}$
). Therefore,
$\mathbb {C}$
). Therefore,
The claim is proved and
![]() $\sigma _M$
is a real structure.
$\sigma _M$
is a real structure.
Recall that
![]() $\mathbb {P}^2_{\mathbb {C}}$
has only one real structure (up to equivalence), namely the standard one, and it is maximal (
$\mathbb {P}^2_{\mathbb {C}}$
has only one real structure (up to equivalence), namely the standard one, and it is maximal (
![]() $b_*(\mathbb {P}^2(\mathbb {C}), \mathbb {F}_2)=b_*(\mathbb {P}^2(\mathbb {R}), \mathbb {F}_2)=3$
). We show that the maximality is inherited by the moduli spaces.
$b_*(\mathbb {P}^2(\mathbb {C}), \mathbb {F}_2)=b_*(\mathbb {P}^2(\mathbb {R}), \mathbb {F}_2)=3$
). We show that the maximality is inherited by the moduli spaces.
Theorem 9.1.
For integers
![]() $r\gt 0, c_1, c_2$
satisfying (23), the moduli space
$r\gt 0, c_1, c_2$
satisfying (23), the moduli space
![]() $M(r, c_1, c_2)$
of stable sheaves on the projective plane equipped with its natural real structure is maximal.
$M(r, c_1, c_2)$
of stable sheaves on the projective plane equipped with its natural real structure is maximal.
Proof.
By construction (using GIT for example),
![]() $M:=M(r, c_1, c_2)$
is a smooth projective variety defined over
$M:=M(r, c_1, c_2)$
is a smooth projective variety defined over
![]() $\mathbb {R}$
. Since
$\mathbb {R}$
. Since
![]() $M$
is a fine moduli space, there is a universal sheaf
$M$
is a fine moduli space, there is a universal sheaf
![]() $\mathcal {E}$
on
$\mathcal {E}$
on
![]() $M\times \mathbb {P}^2$
, which is also defined over
$M\times \mathbb {P}^2$
, which is also defined over
![]() $\mathbb {R}$
. By Ellingsrud and Strømme [Reference Ellingsrud and StrømmeES93], the cohomology ring
$\mathbb {R}$
. By Ellingsrud and Strømme [Reference Ellingsrud and StrømmeES93], the cohomology ring
![]() $H^*(M, \mathbb {Z})$
has no odd cohomology, and it is torsion-free and generated by the elements
$H^*(M, \mathbb {Z})$
has no odd cohomology, and it is torsion-free and generated by the elements
where
![]() $p:M\times S\to M$
is the natural projection,
$p:M\times S\to M$
is the natural projection,
![]() $1\leqslant j\leqslant 3$
and
$1\leqslant j\leqslant 3$
and
![]() $i\in \mathbb {N}$
. Therefore,
$i\in \mathbb {N}$
. Therefore,
![]() $H^*(M, \mathbb {F}_2)$
is also generated, as
$H^*(M, \mathbb {F}_2)$
is also generated, as
![]() $\mathbb {F}_2$
-algebra, by (the images of) the elements in (24). However,
$\mathbb {F}_2$
-algebra, by (the images of) the elements in (24). However,
![]() $R^1p_*(\mathcal {E}(-j))$
is a real algebraic vector bundle on
$R^1p_*(\mathcal {E}(-j))$
is a real algebraic vector bundle on
![]() $M$
, and hence its equivariant Chern class
$M$
, and hence its equivariant Chern class
![]() $c^G_i(R^1p_*(\mathcal {E}(-j)))\in H^*_G(M, \mathbb {F}_2)$
is mapped to
$c^G_i(R^1p_*(\mathcal {E}(-j)))\in H^*_G(M, \mathbb {F}_2)$
is mapped to
![]() $c_i(R^1p_*(\mathcal {E}(-j)))$
via the restriction map
$c_i(R^1p_*(\mathcal {E}(-j)))$
via the restriction map
![]() $H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
. Therefore, the restriction map is surjective and
$H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
. Therefore, the restriction map is surjective and
![]() $M$
is maximal by Proposition 2.3.
$M$
is maximal by Proposition 2.3.
10. Moduli spaces of sheaves on Poisson surfaces
Let
![]() $S$
be a Poisson surface, that is, a smooth projective complex surface with an effective anti-canonical bundle:
$S$
be a Poisson surface, that is, a smooth projective complex surface with an effective anti-canonical bundle:
![]() $H^0(S, -K_S)\neq 0$
. Poisson surfaces are classified by Bartocci and Macrì [Reference Bartocci and MacrìBM05]: they are either symplectic (i.e. K3 or abelian) surfaces or ruled surfaces; see [Reference Bartocci and MacrìBM05, Theorem 1.1] for the precise classification of ruled Poisson surfaces.
$H^0(S, -K_S)\neq 0$
. Poisson surfaces are classified by Bartocci and Macrì [Reference Bartocci and MacrìBM05]: they are either symplectic (i.e. K3 or abelian) surfaces or ruled surfaces; see [Reference Bartocci and MacrìBM05, Theorem 1.1] for the precise classification of ruled Poisson surfaces.
A Mukai vector on
![]() $S$
is an element
$S$
is an element
![]() $v\in \textrm {KU}^0(S)$
. We denote by
$v\in \textrm {KU}^0(S)$
. We denote by
![]() $\textrm {rk}(v)\in \mathbb {Z}$
its rank and by
$\textrm {rk}(v)\in \mathbb {Z}$
its rank and by
![]() $c_i(v)\in H^{2i}(S, \mathbb {Z})$
its
$c_i(v)\in H^{2i}(S, \mathbb {Z})$
its
![]() $i$
th Chern class for
$i$
th Chern class for
![]() $i=1, 2$
. Any coherent sheaf
$i=1, 2$
. Any coherent sheaf
![]() $E$
on
$E$
on
![]() $S$
gives rise to a class in the Grothendieck group
$S$
gives rise to a class in the Grothendieck group
![]() $[E]\in \operatorname {K}^0(S)$
, and its image under the natural map
$[E]\in \operatorname {K}^0(S)$
, and its image under the natural map
![]() $\operatorname {K}^0(S)\to \textrm {KU}^0(S)$
is called the Mukai vector of
$\operatorname {K}^0(S)\to \textrm {KU}^0(S)$
is called the Mukai vector of
![]() $E$
. A polarization
$E$
. A polarization
![]() $H$
is said to be
$H$
is said to be
![]() $v$
-generic if
$v$
-generic if
![]() $H$
-stability coincides with
$H$
-stability coincides with
![]() $H$
-semi-stability for any coherent sheaves with Mukai vector
$H$
-semi-stability for any coherent sheaves with Mukai vector
![]() $v$
. Here and in the following, (semi-)stability is in the sense of Gieseker and Maruyama (see [Reference Huybrechts and LehnHL10]).
$v$
. Here and in the following, (semi-)stability is in the sense of Gieseker and Maruyama (see [Reference Huybrechts and LehnHL10]).
Let
![]() $v$
be a primitive Mukai vector with
$v$
be a primitive Mukai vector with
![]() $\textrm {rk}(v)\gt 0$
and
$\textrm {rk}(v)\gt 0$
and
![]() $c_1(v)\in \operatorname {NS}(S):=H^2(S, \mathbb {Z})\cap H^{1,1}(S)$
, and
$c_1(v)\in \operatorname {NS}(S):=H^2(S, \mathbb {Z})\cap H^{1,1}(S)$
, and
![]() $H$
a
$H$
a
![]() $v$
-generic polarization, which always exists.Footnote
10
Let
$v$
-generic polarization, which always exists.Footnote
10
Let
![]() $M:=M_H(S, v)$
be the moduli space of
$M:=M_H(S, v)$
be the moduli space of
![]() $H$
-stable sheaves on
$H$
-stable sheaves on
![]() $S$
with Mukai vector
$S$
with Mukai vector
![]() $v$
.
$v$
.
For a symplectic surface
![]() $S$
, the moduli space
$S$
, the moduli space
![]() $M$
is a connected smooth projective holomorphic symplectic variety of dimension
$M$
is a connected smooth projective holomorphic symplectic variety of dimension
![]() $2n:=2-\chi (v, v)=(1-r)c_1^2+2rc_2-r^2 \chi (\mathcal {O}_S)+2$
, and is deformation equivalent to the
$2n:=2-\chi (v, v)=(1-r)c_1^2+2rc_2-r^2 \chi (\mathcal {O}_S)+2$
, and is deformation equivalent to the
![]() $n$
th punctual Hilbert scheme
$n$
th punctual Hilbert scheme
![]() $S^{[n]}$
(and hence hyper-Kähler if
$S^{[n]}$
(and hence hyper-Kähler if
![]() $S$
is a K3 surface). This is a theorem established by the works of Mukai [Reference MukaiMuk84], Göttsche and Huybrechts [Reference Göttsche and HuybrechtsGH96], O’Grady [Reference O’GradyO’G97], Yoshioka [Reference YoshiokaYos99], etc; see [Reference Huybrechts and LehnHL10, Theorem 6.2.5].
$S$
is a K3 surface). This is a theorem established by the works of Mukai [Reference MukaiMuk84], Göttsche and Huybrechts [Reference Göttsche and HuybrechtsGH96], O’Grady [Reference O’GradyO’G97], Yoshioka [Reference YoshiokaYos99], etc; see [Reference Huybrechts and LehnHL10, Theorem 6.2.5].
For a ruled Poisson surface
![]() $S$
, the moduli space
$S$
, the moduli space
![]() $M$
, if non-empty, is a connected smooth projective variety of dimension
$M$
, if non-empty, is a connected smooth projective variety of dimension
![]() $1-\chi (v, v)=(1-r)c_1^2+2rc_2-r^2 \chi (\mathcal {O}_S)+1$
with a Poisson structure. This is due to Bottacin [Reference BottacinBot95] (based on Tyurin [Reference TyurinTyu88]).
$1-\chi (v, v)=(1-r)c_1^2+2rc_2-r^2 \chi (\mathcal {O}_S)+1$
with a Poisson structure. This is due to Bottacin [Reference BottacinBot95] (based on Tyurin [Reference TyurinTyu88]).
Theorem 10.1.
Let
![]() $(S, \sigma )$
be a Poisson surface with a real structure. Let
$(S, \sigma )$
be a Poisson surface with a real structure. Let
![]() $v\in \textrm {KU}^0(S)$
be a primitive Mukai vector with
$v\in \textrm {KU}^0(S)$
be a primitive Mukai vector with
![]() $\textrm {rk}(v)\gt 0$
and satisfying
$\textrm {rk}(v)\gt 0$
and satisfying
![]() $c_1(v)\in \operatorname {NS}(S)$
and
$c_1(v)\in \operatorname {NS}(S)$
and
![]() $\sigma ^*(c_1(v))=-c_1(v)$
. Let
$\sigma ^*(c_1(v))=-c_1(v)$
. Let
![]() $H$
be a real algebraic ample line bundle that is
$H$
be a real algebraic ample line bundle that is
![]() $v$
-generic. Then
$v$
-generic. Then
![]() $\sigma$
induces a natural real structure on
$\sigma$
induces a natural real structure on
![]() $M:=M_H(S, v)$
. If
$M:=M_H(S, v)$
. If
![]() $S$
is K-maximal (Definition 4.1) in the sense that the natural maps
$S$
is K-maximal (Definition 4.1) in the sense that the natural maps
![]() $\textrm {KR}^i(S)\to \textrm {KU}^i(S)$
are surjective for
$\textrm {KR}^i(S)\to \textrm {KU}^i(S)$
are surjective for
![]() $i=0, 1$
, then
$i=0, 1$
, then
![]() $M$
is maximal.
$M$
is maximal.
Proof.
Let
![]() $\mathcal {E}$
be a (quasi)-universal sheaf on
$\mathcal {E}$
be a (quasi)-universal sheaf on
![]() $M\times S$
, which defines a class
$M\times S$
, which defines a class
![]() $e\in \textrm {KU}^0(M\times S)$
; see [Reference MarkmanMar07, Section 3] for the detailed construction of
$e\in \textrm {KU}^0(M\times S)$
; see [Reference MarkmanMar07, Section 3] for the detailed construction of
![]() $e$
in the absence of universal sheaf. By construction,
$e$
in the absence of universal sheaf. By construction,
![]() $\mathcal {E}$
is a real sheaf, and hence the class
$\mathcal {E}$
is a real sheaf, and hence the class
![]() $e\in \textrm {KU}^0(M\times S)$
is the image of a class
$e\in \textrm {KU}^0(M\times S)$
is the image of a class
![]() $\widetilde {e}\in \textrm {KR}^0(M\times S)$
.
$\widetilde {e}\in \textrm {KR}^0(M\times S)$
.
In the following, for simplicity, we denote
![]() $\textrm {KU}^*:= \textrm {KU}^0\oplus \textrm {KU}^1$
and
$\textrm {KU}^*:= \textrm {KU}^0\oplus \textrm {KU}^1$
and
![]() $\textrm {KR}^*:= \textrm {KR}^0\oplus \textrm {KR}^1$
. Let
$\textrm {KR}^*:= \textrm {KR}^0\oplus \textrm {KR}^1$
. Let
![]() $p_1\ \textrm{and}\ p_2$
be the projections from
$p_1\ \textrm{and}\ p_2$
be the projections from
![]() $M\times S$
to
$M\times S$
to
![]() $M$
and
$M$
and
![]() $S$
, respectively. Since
$S$
, respectively. Since
![]() $\textrm {KU}^*(S)$
is torsion-free (for any Poisson surface
$\textrm {KU}^*(S)$
is torsion-free (for any Poisson surface
![]() $S$
), we have the Künneth decomposition for topological K-theory:
$S$
), we have the Künneth decomposition for topological K-theory:
Via the above decomposition, we write the following equality in
![]() $\textrm {KU}^0(M\times S)$
:
$\textrm {KU}^0(M\times S)$
:
where
![]() $\{x_i\}_i$
is a basis of
$\{x_i\}_i$
is a basis of
![]() $\textrm {KU}^*(S)$
, and
$\textrm {KU}^*(S)$
, and
![]() $e_i\in \textrm {KU}^*(M)$
.
$e_i\in \textrm {KU}^*(M)$
.
By Markman [Reference MarkmanMar07, Theorem 1], the cohomology ring
![]() $H^*(M, \mathbb {Z})$
is torsion-free and generated by Chern classes
$H^*(M, \mathbb {Z})$
is torsion-free and generated by Chern classes
![]() $\{c_j(e_i)\}_{i,j}$
, where
$\{c_j(e_i)\}_{i,j}$
, where
![]() $j$
runs through
$j$
runs through
![]() $\mathbb {N}+\frac {1}{2}$
if
$\mathbb {N}+\frac {1}{2}$
if
![]() $e_i\in \textrm {KU}^1(M)$
; see [Reference MarkmanMar07, Definition 19] for the definition of Chern classes of elements in odd K-theory. Therefore,
$e_i\in \textrm {KU}^1(M)$
; see [Reference MarkmanMar07, Definition 19] for the definition of Chern classes of elements in odd K-theory. Therefore,
![]() $H^*(M, \mathbb {F}_2)$
is also generated by
$H^*(M, \mathbb {F}_2)$
is also generated by
![]() $\{c_j(e_i)\}_{i,j}$
. We only need to prove that every generator
$\{c_j(e_i)\}_{i,j}$
. We only need to prove that every generator
![]() $c_j(e_i)\in H^{2j}(M, \mathbb {F}_2)$
has a preimage in
$c_j(e_i)\in H^{2j}(M, \mathbb {F}_2)$
has a preimage in
![]() $H^{2j}_G(M, \mathbb {F}_2)$
.
$H^{2j}_G(M, \mathbb {F}_2)$
.
Since the pairing
is perfect (see [Reference MarkmanMar07, Remark 18]), one can find a dual basis
![]() $\{y_i\}_i$
of
$\{y_i\}_i$
of
![]() $\textrm {KU}^*(S)$
, i.e.
$\textrm {KU}^*(S)$
, i.e.
![]() $\chi (x_i^\vee \otimes y_j)=\delta _{ij}$
. Since
$\chi (x_i^\vee \otimes y_j)=\delta _{ij}$
. Since
![]() $\textrm {KR}^*(S)\to \textrm {KU}^*(S)$
is surjective by assumption, we have that, for each
$\textrm {KR}^*(S)\to \textrm {KU}^*(S)$
is surjective by assumption, we have that, for each
![]() $i$
, there exists
$i$
, there exists
![]() $\widetilde {y_i}\in \textrm {KR}^*(S)$
whose image in
$\widetilde {y_i}\in \textrm {KR}^*(S)$
whose image in
![]() $\textrm {KU}^*(S)$
is
$\textrm {KU}^*(S)$
is
![]() $y_i$
.
$y_i$
.
Consider the element
The image of
![]() $\widetilde {e_i}$
under the map
$\widetilde {e_i}$
under the map
![]() $\textrm {KR}^*(M)\to \textrm {KU}^*(M)$
is computed as follows using (25):
$\textrm {KR}^*(M)\to \textrm {KU}^*(M)$
is computed as follows using (25):
We obtain that, for any
![]() $i$
, the class
$i$
, the class
![]() $\widetilde {e_i}\in \textrm {KR}^*(M)$
is mapped to
$\widetilde {e_i}\in \textrm {KR}^*(M)$
is mapped to
![]() $e_i\in \textrm {KU}^*(M)$
. Therefore, the equivariant Chern class
$e_i\in \textrm {KU}^*(M)$
. Therefore, the equivariant Chern class
![]() $c_j^G(\widetilde {e_i})\in H_G^{2j}(M, \mathbb {F}_2)$
is mapped to the Chern class
$c_j^G(\widetilde {e_i})\in H_G^{2j}(M, \mathbb {F}_2)$
is mapped to the Chern class
![]() $c_j(e_i)\in H^{2j}(M, \mathbb {F}_2)$
via the restriction map. As
$c_j(e_i)\in H^{2j}(M, \mathbb {F}_2)$
via the restriction map. As
![]() $\{c_j(e_i)\}$
are generators, the restriction map
$\{c_j(e_i)\}$
are generators, the restriction map
![]() $H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
is surjective, and
$H^*_G(M, \mathbb {F}_2)\to H^*(M, \mathbb {F}_2)$
is surjective, and
![]() $M$
is maximal by Proposition 2.3.
$M$
is maximal by Proposition 2.3.
To provide examples where Theorem10.1 applies, let us give the following generalization of Theorem9.1.
Corollary 10.2 (Rational real Poisson surface). Let
![]() $S$
be a Poisson surface with a real structure
$S$
be a Poisson surface with a real structure
![]() $\sigma$
such that it is
$\sigma$
such that it is
![]() $\mathbb {R}$
-rational. Let
$\mathbb {R}$
-rational. Let
![]() $v$
be a primitive Mukai vector satisfying
$v$
be a primitive Mukai vector satisfying
![]() $\textrm {rk}(v)\gt 0$
and
$\textrm {rk}(v)\gt 0$
and
![]() $\sigma ^*(c_1(v))=-c_1(v)$
. Let
$\sigma ^*(c_1(v))=-c_1(v)$
. Let
![]() $H$
be a real algebraic ample line bundle that is
$H$
be a real algebraic ample line bundle that is
![]() $v$
-generic. If
$v$
-generic. If
![]() $(S, \sigma )$
is maximal, then
$(S, \sigma )$
is maximal, then
![]() $M_H(S, v)$
, equipped with the natural real structure, is also maximal.
$M_H(S, v)$
, equipped with the natural real structure, is also maximal.
11. Real motives, equivariant formality, and maximality
The notion of motive was invented by Grothendieck around 1960 to unify various cohomology theories and to deal with problems involving algebraic cycles. It has become a standard and powerful tool nowadays throughout algebraic geometry. See [Reference AndréAnd04] for an introduction. In this section, we would like to explain the relation between the maximality of real varieties and their motives. Although not logically necessary for the results obtained in this paper, we highlight the following principle which underlies the whole paper.
Principle: The maximality of real varieties is a motivicproperty calledequivariant formality, and new maximal varieties can be constructed as thosemotivatedby maximal ones.
For the precise meaning of the principle, see Definition 11.2 and Corollary 11.7. We switch to the algebraic notation in this section: for an algebraic variety
![]() $X$
defined over
$X$
defined over
![]() $\mathbb {R}$
, the complex analytic space is denoted by
$\mathbb {R}$
, the complex analytic space is denoted by
![]() $X(\mathbb {C}):=X_{\mathbb {C}}^{an}$
. In particular,
$X(\mathbb {C}):=X_{\mathbb {C}}^{an}$
. In particular,
![]() $(X\times _{\mathbb {R}}Y)(\mathbb {C})=X(\mathbb {C})\times Y(\mathbb {C})$
.
$(X\times _{\mathbb {R}}Y)(\mathbb {C})=X(\mathbb {C})\times Y(\mathbb {C})$
.
11.1 Motives
Let us briefly recall some basic notions on motives; see [Reference AndréAnd04] for a detailed account.
Definition 11.1 (Real motives). Fix a commutative ring
![]() $F$
as the coefficient ring. In this paper,
$F$
as the coefficient ring. In this paper,
![]() $F=\mathbb {Z}$
,
$F=\mathbb {Z}$
,
![]() $\mathbb {Q}$
, or
$\mathbb {Q}$
, or
![]() $\mathbb {F}_2$
, etc.
$\mathbb {F}_2$
, etc.
(i) The category of Chow motives over the field
![]() $\mathbb {R}$
with coefficients in
$\mathbb {R}$
with coefficients in
![]() $F$
, denoted by
$F$
, denoted by
![]() $\textrm {CHM}(\mathbb {R})_F$
, is defined as follows.
$\textrm {CHM}(\mathbb {R})_F$
, is defined as follows.
- An object, called a Chow motive, is a triple
![]() $(X, p, n)$
, where
$(X, p, n)$
, where
![]() $n$
is an integer,
$n$
is an integer,
![]() $X$
is a smooth projective variety over
$X$
is a smooth projective variety over
![]() $\mathbb {R}$
of dimension
$\mathbb {R}$
of dimension
![]() $d_X$
and
$d_X$
and
![]() $p\in \textrm {CH}^{d_X}(X\times _{\mathbb {R}} X)_F$
is an algebraic cycle (modulo rational equivalence) in
$p\in \textrm {CH}^{d_X}(X\times _{\mathbb {R}} X)_F$
is an algebraic cycle (modulo rational equivalence) in
![]() $X\times _{\mathbb {R}} X$
with
$X\times _{\mathbb {R}} X$
with
![]() $F$
-coefficients such that
$F$
-coefficients such that
![]() $p\circ p=p$
; here
$p\circ p=p$
; here
![]() $\circ$
denotes the composition of correspondences.
$\circ$
denotes the composition of correspondences.
- A morphism between two Chow motives
![]() $(X, p, n)$
and
$(X, p, n)$
and
![]() $(Y, q, m)$
is an element in the group
$(Y, q, m)$
is an element in the group
The composition of morphisms is given by the composition of correspondences.
- There is a natural (contravariant) functor of ‘taking Chow motives’:
 \begin{align*} \text {(Smooth projective $\mathbb {R}$-varieties, $\mathbb {R}$-morphisms)}^{\operatorname {op}} & \to \textrm {CHM}(\mathbb {R})_F\\ X&\mapsto \mathfrak {h}(X):=(X, \Delta _X, 0)\\ (f\colon Y\to X) & \mapsto \Gamma _f\in \textrm {CH}^{d_X}(X\times _{\mathbb {R}} Y)_F \end{align*}
\begin{align*} \text {(Smooth projective $\mathbb {R}$-varieties, $\mathbb {R}$-morphisms)}^{\operatorname {op}} & \to \textrm {CHM}(\mathbb {R})_F\\ X&\mapsto \mathfrak {h}(X):=(X, \Delta _X, 0)\\ (f\colon Y\to X) & \mapsto \Gamma _f\in \textrm {CH}^{d_X}(X\times _{\mathbb {R}} Y)_F \end{align*}
where
![]() $\Delta _X\in \textrm {CH}^{d_X}(X\times _{\mathbb {R}} X)_F$
is the class of the diagonal and
$\Delta _X\in \textrm {CH}^{d_X}(X\times _{\mathbb {R}} X)_F$
is the class of the diagonal and
![]() $\Gamma _f$
is the graph of
$\Gamma _f$
is the graph of
![]() $f$
.
$f$
.
The category
![]() $\textrm {CHM}(\mathbb {R})_F$
is an
$\textrm {CHM}(\mathbb {R})_F$
is an
![]() $F$
-linear, idempotent complete, rigid tensor category, with unit object
$F$
-linear, idempotent complete, rigid tensor category, with unit object
![]() $\unicode {x1D7D9}=(\textrm {Spec}(\mathbb {R}), \Delta, 0)$
,
$\unicode {x1D7D9}=(\textrm {Spec}(\mathbb {R}), \Delta, 0)$
,
![]() $(X, p, n)\otimes (Y, q, m):= (X\times _{\mathbb {R}} Y, p\times q, m+n)$
and
$(X, p, n)\otimes (Y, q, m):= (X\times _{\mathbb {R}} Y, p\times q, m+n)$
and
![]() $(X, p, n)^\vee := (X, {}^tp, d_X-n)$
, where
$(X, p, n)^\vee := (X, {}^tp, d_X-n)$
, where
![]() ${}^tp$
is the transpose of
${}^tp$
is the transpose of
![]() $p$
(i.e. its image under the involution on
$p$
(i.e. its image under the involution on
![]() $X\times _{\mathbb {R}} X$
) swapping two factors. For an integer
$X\times _{\mathbb {R}} X$
) swapping two factors. For an integer
![]() $n$
, the Tate object is
$n$
, the Tate object is
![]() $\unicode {x1D7D9}(n):=(\textrm {Spec}(\mathbb {R}), \Delta, n)$
.
$\unicode {x1D7D9}(n):=(\textrm {Spec}(\mathbb {R}), \Delta, n)$
.
(ii) Similarly, by replacing the Chow groups by the groups of algebraic cycles modulo homological equivalence in the above definition, we obtain the category of homological (or Grothendieck) motives, denoted by
![]() $\textrm {Mot}(\mathbb {R})_F$
. The (contravariant) functor of taking homological motives is denoted by
$\textrm {Mot}(\mathbb {R})_F$
. The (contravariant) functor of taking homological motives is denoted by
![]() $X\mapsto M(X)$
.
$X\mapsto M(X)$
.
(iii) Since rational equivalence is finer than homological equivalence, we have a natural functor
![]() $\textrm {CHM}(\mathbb {R})_F\to \textrm {Mot}(\mathbb {R})_F$
.
$\textrm {CHM}(\mathbb {R})_F\to \textrm {Mot}(\mathbb {R})_F$
.
11.2 Realizations
It is easy to check that any (generalized) cohomological theory (like Chow group
![]() $\textrm {CH}^*$
, cohomology
$\textrm {CH}^*$
, cohomology
![]() $H^*$
, equivariant cohomology
$H^*$
, equivariant cohomology
![]() $H_G^*$
, K-theory, topological K-theory, etc.) that behaves well with respect to correspondences (i.e. with respect to pullbacks, push-forwards and intersection products) can be extended to appropriate categories of motives, called realizations. Let us mention some examples. Let
$H_G^*$
, K-theory, topological K-theory, etc.) that behaves well with respect to correspondences (i.e. with respect to pullbacks, push-forwards and intersection products) can be extended to appropriate categories of motives, called realizations. Let us mention some examples. Let
![]() $\textrm {Mod}_F$
(respectively,
$\textrm {Mod}_F$
(respectively,
![]() $\textrm {Mod}_F^{\mathbb {Z}}$
) be the category of (respectively, graded)
$\textrm {Mod}_F^{\mathbb {Z}}$
) be the category of (respectively, graded)
![]() $F$
-modules.
$F$
-modules.
-
(i) (Chow group). Define
It follows from the definition that the Chow group of a Chow motive \begin{align*} \textrm {CH}^*\colon \textrm {CHM}(\mathbb {R})_F \to & \textrm {Mod}_F^{\mathbb {Z}}\\ (X, p, n)&\mapsto \textrm {Im}(p_*\colon \textrm {CH}^{*+n}(X)_F\to \textrm {CH}^{*+n}(X)_F). \end{align*}
\begin{align*} \textrm {CH}^*\colon \textrm {CHM}(\mathbb {R})_F \to & \textrm {Mod}_F^{\mathbb {Z}}\\ (X, p, n)&\mapsto \textrm {Im}(p_*\colon \textrm {CH}^{*+n}(X)_F\to \textrm {CH}^{*+n}(X)_F). \end{align*}
 $M$
is just a
$M$
is just a
 $\textrm {Hom}$
group in the category
$\textrm {Hom}$
group in the category
 $\textrm {CHM}(\mathbb {R})_F$
:
$\textrm {CHM}(\mathbb {R})_F$
: \begin{align*}\textrm {CH}^i(M)_F=\textrm {Hom}(\unicode {x1D7D9}(-i), M).\end{align*}
\begin{align*}\textrm {CH}^i(M)_F=\textrm {Hom}(\unicode {x1D7D9}(-i), M).\end{align*}
-
(ii) (Equivariant cohomology). Let
 $G=\operatorname {Gal}(\mathbb {C}/\mathbb {R})$
. For any integers
$G=\operatorname {Gal}(\mathbb {C}/\mathbb {R})$
. For any integers
 $i, j$
, we havewhere
$i, j$
, we havewhere \begin{align*} H_G^i(-, F(j))\colon \textrm {Mot}(\mathbb {R})_F &\to \textrm {Mod}_F\\ (X, p, n)&\mapsto \textrm {Im}(\textrm {cl}_G(p)_*\colon H^{i+2n}_G(X(\mathbb {C}), F(j+n))\to H^{i+2n}_G(X(\mathbb {C}), F(j+n))), \end{align*}
\begin{align*} H_G^i(-, F(j))\colon \textrm {Mot}(\mathbb {R})_F &\to \textrm {Mod}_F\\ (X, p, n)&\mapsto \textrm {Im}(\textrm {cl}_G(p)_*\colon H^{i+2n}_G(X(\mathbb {C}), F(j+n))\to H^{i+2n}_G(X(\mathbb {C}), F(j+n))), \end{align*}
 $F(j)=\sqrt {-1}^j\mathbb {Z}$
as
$F(j)=\sqrt {-1}^j\mathbb {Z}$
as
 $G$
-module.
$G$
-module.
Here we used the existence of the equivariant cycle class map: for any smooth projective real variety
 $W$
, we havewhich is compatible with the functorialities and cup-product of equivariant cohomology, thanks to Krasnov [Reference KrasnovKra91]. Let us also mention that, when
$W$
, we havewhich is compatible with the functorialities and cup-product of equivariant cohomology, thanks to Krasnov [Reference KrasnovKra91]. Let us also mention that, when \begin{align*}\textrm {cl}_G\colon \textrm {CH}^*(W)_F\to H^{2*}_G(W(\mathbb {C}), F(*)),\end{align*}
\begin{align*}\textrm {cl}_G\colon \textrm {CH}^*(W)_F\to H^{2*}_G(W(\mathbb {C}), F(*)),\end{align*}
 $F$
is torsion,
$F$
is torsion,
 $H_G^i(-, F(j))$
is canonically identified with the étale cohomology
$H_G^i(-, F(j))$
is canonically identified with the étale cohomology
 $H_{\mathrm {\acute {e}t}}^i(-, F(j))$
(see [Reference ScheidererSch94, Corollary 15.3.1]), and the standard compatibility with étale cycle class map yields the étale realization functor.
$H_{\mathrm {\acute {e}t}}^i(-, F(j))$
(see [Reference ScheidererSch94, Corollary 15.3.1]), and the standard compatibility with étale cycle class map yields the étale realization functor.
-
(iii) (Cohomology of complexification). For motives over
 $\mathbb {C}$
, we have the realization of singular cohomology:where
$\mathbb {C}$
, we have the realization of singular cohomology:where \begin{align*} H^*\colon \textrm {Mot}(\mathbb {C})_F&\to \textrm {Mod}_F^{\mathbb {Z}}\\ (X, p, n)& \mapsto \textrm {Im}(\textrm {cl}(p)_*\colon H^{*+2n}(X(\mathbb {C}), F)\to H^{*+2n}(X(\mathbb {C}), F)), \end{align*}
\begin{align*} H^*\colon \textrm {Mot}(\mathbb {C})_F&\to \textrm {Mod}_F^{\mathbb {Z}}\\ (X, p, n)& \mapsto \textrm {Im}(\textrm {cl}(p)_*\colon H^{*+2n}(X(\mathbb {C}), F)\to H^{*+2n}(X(\mathbb {C}), F)), \end{align*}
 $\textrm {cl}$
is the usual (complex) cycle class map. By composing with the complexification functor
$\textrm {cl}$
is the usual (complex) cycle class map. By composing with the complexification functor
 $-_{\mathbb {C}}\colon \textrm {Mot}(\mathbb {R})_F\to \textrm {Mot}(\mathbb {C})_F$
, we get the following realization, still denoted by
$-_{\mathbb {C}}\colon \textrm {Mot}(\mathbb {R})_F\to \textrm {Mot}(\mathbb {C})_F$
, we get the following realization, still denoted by
 $H$
:In fact, when
$H$
:In fact, when \begin{align*} H^*\colon \textrm {Mot}(\mathbb {R})_F&\to \textrm {Mod}_F^{\mathbb {Z}}\\ M=(X, p, n)& \mapsto H^*(M_{\mathbb {C}}):= \textrm {Im}(\textrm {cl}(p_{\mathbb {C}})_*\colon H^{*+2n}(X(\mathbb {C}), F)\to H^{*+2n}(X(\mathbb {C}), F)). \end{align*}
\begin{align*} H^*\colon \textrm {Mot}(\mathbb {R})_F&\to \textrm {Mod}_F^{\mathbb {Z}}\\ M=(X, p, n)& \mapsto H^*(M_{\mathbb {C}}):= \textrm {Im}(\textrm {cl}(p_{\mathbb {C}})_*\colon H^{*+2n}(X(\mathbb {C}), F)\to H^{*+2n}(X(\mathbb {C}), F)). \end{align*}
 $F=\mathbb {Z}$
or
$F=\mathbb {Z}$
or
 $\mathbb {Q}$
, we can further enhance the realization functor into a functor with target the category of (polarizable) Hodge structures, still denoted by
$\mathbb {Q}$
, we can further enhance the realization functor into a functor with target the category of (polarizable) Hodge structures, still denoted by
 $H^*$
:
$H^*$
: \begin{align*} H^*\colon \textrm {Mot}(\mathbb {R})_F\to \operatorname {HS}_F^{\mathbb {Z}}. \end{align*}
\begin{align*} H^*\colon \textrm {Mot}(\mathbb {R})_F\to \operatorname {HS}_F^{\mathbb {Z}}. \end{align*}
-
(iv) (Cohomology of real loci). To each real variety
 $X$
, one can associate the cohomology of its real locus
$X$
, one can associate the cohomology of its real locus
 $H^*(X(\mathbb {R}), \mathbb {F}_2)$
. We claim that this extends to a realization functor:Here we used that, for any smooth projective real variety
$H^*(X(\mathbb {R}), \mathbb {F}_2)$
. We claim that this extends to a realization functor:Here we used that, for any smooth projective real variety \begin{align*} H\!\mathbb {R}^*\colon \textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}&\to \textrm {Mod}_{\mathbb {F}_2}^{\mathbb {Z}}\\ (X, p, n)& \mapsto \textrm {Im}(\textrm {cl}_R(p)_*\colon H^{*+n}(X(\mathbb {R}), \mathbb {F}_2)\to H^{*+n}(X(\mathbb {R}), \mathbb {F}_2)). \end{align*}
\begin{align*} H\!\mathbb {R}^*\colon \textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}&\to \textrm {Mod}_{\mathbb {F}_2}^{\mathbb {Z}}\\ (X, p, n)& \mapsto \textrm {Im}(\textrm {cl}_R(p)_*\colon H^{*+n}(X(\mathbb {R}), \mathbb {F}_2)\to H^{*+n}(X(\mathbb {R}), \mathbb {F}_2)). \end{align*}
 $W$
, we have the Borel–Haefliger real cycle class map [Reference Borel and HaefligerBH61]which is compatible with pullbacks, push-forwards and the intersection product. The latter fact can be justified as follows: thanks to Krasnov [Reference KrasnovKra94], the Borel–Haefliger cycle class map is the composition of the equivariant cycle class map
$W$
, we have the Borel–Haefliger real cycle class map [Reference Borel and HaefligerBH61]which is compatible with pullbacks, push-forwards and the intersection product. The latter fact can be justified as follows: thanks to Krasnov [Reference KrasnovKra94], the Borel–Haefliger cycle class map is the composition of the equivariant cycle class map \begin{align*}\textrm {cl}_R\colon \textrm {CH}^*(W)\to H^*(W(\mathbb {R}), \mathbb {F}_2),\end{align*}
\begin{align*}\textrm {cl}_R\colon \textrm {CH}^*(W)\to H^*(W(\mathbb {R}), \mathbb {F}_2),\end{align*}
 $\textrm {cl}_G$
with the map of restricting to the real locus constructed in [Reference KrasnovKra94]:The compatibility with respect to the pullbacks and the intersection product is easy to check while the compatibility with respect to push-forwards can be found in [Reference Benoist and WittenbergBW20, Theorem 1.21 and Proposition 1.22].
$\textrm {cl}_G$
with the map of restricting to the real locus constructed in [Reference KrasnovKra94]:The compatibility with respect to the pullbacks and the intersection product is easy to check while the compatibility with respect to push-forwards can be found in [Reference Benoist and WittenbergBW20, Theorem 1.21 and Proposition 1.22]. \begin{align*}H^{2*}_G(W, \mathbb {F}_2)\to H^*(W(\mathbb {R}), \mathbb {F}_2).\end{align*}
\begin{align*}H^{2*}_G(W, \mathbb {F}_2)\to H^*(W(\mathbb {R}), \mathbb {F}_2).\end{align*}
-
(v) We have various natural transformations between these realization functors on motives. For example, for any Chow motive
 $M$
, we have
$M$
, we have-
– the restriction map
 $H^i_G(M, F(j))\to H^i(M_{\mathbb {C}}, F)$
;
$H^i_G(M, F(j))\to H^i(M_{\mathbb {C}}, F)$
; -
– the equivariant cycle class map
 $\textrm {cl}_G\colon \textrm {CH}^*(M)\to H^{2*}_G(M, \mathbb {Z}(*))$
;
$\textrm {cl}_G\colon \textrm {CH}^*(M)\to H^{2*}_G(M, \mathbb {Z}(*))$
; -
– Krasnov’s map of restricting to real loci
 $H^{2*}_G(M, \mathbb {F}_2)\to H\!\mathbb {R}^*(M, \mathbb {F}_2)$
;
$H^{2*}_G(M, \mathbb {F}_2)\to H\!\mathbb {R}^*(M, \mathbb {F}_2)$
; -
– composing the previous two morphisms, we get Borel–Haefliger’s real cycle class map for real motives
 $\textrm {cl}_R\colon \textrm {CH}^*(M)\to H\!\mathbb {R}^*(M, \mathbb {F}_2)$
.
$\textrm {cl}_R\colon \textrm {CH}^*(M)\to H\!\mathbb {R}^*(M, \mathbb {F}_2)$
.
-
We can now generalize the notion of maximality as follows, in view of Proposition 2.3.
Definition 11.2 (Equivariantly formal real motives). A homological motive
![]() $M\in \textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
is said to be equivariantly formal if the restriction morphism
$M\in \textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
is said to be equivariantly formal if the restriction morphism
![]() $H^*_G(M, \mathbb {F}_2)\to H^*(M_{\mathbb {C}}, \mathbb {F}_2)$
is surjective.
$H^*_G(M, \mathbb {F}_2)\to H^*(M_{\mathbb {C}}, \mathbb {F}_2)$
is surjective.
By Proposition 2.3, a smooth projective real variety
![]() $X$
is maximal if and only if its homological motive
$X$
is maximal if and only if its homological motive
![]() $M(X)\in \textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
is equivariantly formal. Of course, we have the following more naive generalization of maximality (and Hodge expressivity) to motives.
$M(X)\in \textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
is equivariantly formal. Of course, we have the following more naive generalization of maximality (and Hodge expressivity) to motives.
Definition 11.3 (Maximal and Hodge expressive motives). A homological motive
![]() $M\in \textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
is said to be maximal if
$M\in \textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
is said to be maximal if
Similarly,
![]() $M\in \textrm {Mot}(\mathbb {R})$
is said to be Hodge expressive if
$M\in \textrm {Mot}(\mathbb {R})$
is said to be Hodge expressive if
![]() $H^*(M, \mathbb {Z})$
is torsion-free and, for any
$H^*(M, \mathbb {Z})$
is torsion-free and, for any
![]() $p\in \mathbb {Z}$
,
$p\in \mathbb {Z}$
,
where
![]() $H^{p,q}(M)$
is the
$H^{p,q}(M)$
is the
![]() $(p,q)$
-component of the Hodge structure
$(p,q)$
-component of the Hodge structure
![]() $H^*(M_{\mathbb {C}}, \mathbb {Q})$
.
$H^*(M_{\mathbb {C}}, \mathbb {Q})$
.
Remark 11.4. The notions of maximality and Hodge expressivity for real motives defined above do not seem very useful, since it is a priori not inherited by submotives; see Remark 11.8.
11.3 Inheriting maximality by motivation
Recall that the category
![]() $\textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
is a tensor category. We first check that the standard tensor operations in
$\textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
is a tensor category. We first check that the standard tensor operations in
![]() $\textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
preserve equivariant formality.
$\textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
preserve equivariant formality.
It is clear from Definition 11.2 that the direct sum of some equivariantly formal motives is equivariantly formal, and a direct summand of an equivariantly formal motive is equivariantly formal, and one can check directly (using the maximality of
![]() $\mathbb {P}^n_{\mathbb {R}}$
for example) that the Tate motives
$\mathbb {P}^n_{\mathbb {R}}$
for example) that the Tate motives
![]() $\unicode {x1D7D9}(n)$
are equivariantly formal for all
$\unicode {x1D7D9}(n)$
are equivariantly formal for all
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
Next, recall that the tensor product of motives is given essentially by the fiber product (see Definition 11.1). Similarly to Lemma 3.1, equivariant formality is preserved by the tensor product of motives.
Lemma 11.5 (Tensor product). If
![]() $M_1, \ldots, M_n\in \textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
are equivariantly formal real motives, then
$M_1, \ldots, M_n\in \textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
are equivariantly formal real motives, then
![]() $M_1\otimes \cdots \otimes M_n$
is also equivariantly formal. In particular, Tate twists of equivariantly formal real motives are equivariantly formal.
$M_1\otimes \cdots \otimes M_n$
is also equivariantly formal. In particular, Tate twists of equivariantly formal real motives are equivariantly formal.
Proof.
By induction, it is enough to show the case where
![]() $n=2$
. Consider the following commutative diagram, where we omit the coefficient
$n=2$
. Consider the following commutative diagram, where we omit the coefficient
![]() $\mathbb {F}_2$
:
$\mathbb {F}_2$
:

where the horizontal arrows are restriction maps, the right vertical arrow is given by the exterior cup product of singular cohomology, the left vertical arrow is the composition of the exterior cup product for equivariant cohomology followed by the restriction map from
![]() $G\times G$
to
$G\times G$
to
![]() $\Delta _G$
:
$\Delta _G$
:
(or equivalently, since we are using
![]() $\mathbb {F}_2$
-coefficients, we can identify the equivariant realization with the étale realization, so the left arrow is given by the exterior cup product for étale cohomology).
$\mathbb {F}_2$
-coefficients, we can identify the equivariant realization with the étale realization, so the left arrow is given by the exterior cup product for étale cohomology).
Since the right vertical arrow is an isomorphism by the Künneth formula and the top arrow is surjective by assumption, we can conclude that the bottom arrow is also surjective.
Fix a category of motives
![]() $\mathcal {C} =\textrm {CHM}(\mathbb {R})_F$
or
$\mathcal {C} =\textrm {CHM}(\mathbb {R})_F$
or
![]() $\textrm {Mot}(\mathbb {R})_F$
. For a collection of (Chow or homological) motives
$\textrm {Mot}(\mathbb {R})_F$
. For a collection of (Chow or homological) motives
![]() $\{M_i\}_{i\in I}$
, we denote by
$\{M_i\}_{i\in I}$
, we denote by
![]() $\langle M_i; i\in I\rangle ^{\otimes }$
the thick tensor subcategory generated by the
$\langle M_i; i\in I\rangle ^{\otimes }$
the thick tensor subcategory generated by the
![]() $M_i$
, that is, the smallest
$M_i$
, that is, the smallest
![]() $F$
-linear subcategory of
$F$
-linear subcategory of
![]() $\mathcal {C}$
containing all
$\mathcal {C}$
containing all
![]() $M_i$
and closed under isomorphisms, direct sums, tensor products, direct summands and Tate twists. By Lemma 11.5, if all
$M_i$
and closed under isomorphisms, direct sums, tensor products, direct summands and Tate twists. By Lemma 11.5, if all
![]() $M_i$
are equivariantly formal motives, then every object in the category
$M_i$
are equivariantly formal motives, then every object in the category
![]() $\langle M_i; i\in I\rangle ^{\otimes }_{\textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}}$
is equivariantly formal.
$\langle M_i; i\in I\rangle ^{\otimes }_{\textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}}$
is equivariantly formal.
Definition 11.6 (Motivation). A real variety
![]() $Y$
is said to be motivated by a collection of smooth projective real varieties
$Y$
is said to be motivated by a collection of smooth projective real varieties
![]() $\{X_i\}_{i\in I}$
if its homological motive with
$\{X_i\}_{i\in I}$
if its homological motive with
![]() $\mathbb {F}_2$
-coefficients
$\mathbb {F}_2$
-coefficients
![]() $M(Y)$
lies in the subcategory
$M(Y)$
lies in the subcategory
![]() $\langle M(X_i); i\in I\rangle ^{\otimes }_{\textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}}$
.
$\langle M(X_i); i\in I\rangle ^{\otimes }_{\textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}}$
.
The main point of this section is the following observation.
Corollary 11.7.
A real variety
![]() $Y$
motivated by a collection of maximal real varieties
$Y$
motivated by a collection of maximal real varieties
![]() $\{X_i\}_{i\in I}$
is maximal.
$\{X_i\}_{i\in I}$
is maximal.
Proof.
It is almost evident: if
![]() $Y$
is motivated by
$Y$
is motivated by
![]() $\{X_i\}_{i\in I}$
, that is, in the category
$\{X_i\}_{i\in I}$
, that is, in the category
![]() $\textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
,
$\textrm {Mot}(\mathbb {R})_{\mathbb {F}_2}$
,
Since
![]() $M(X_i)$
is equivariantly formal for any
$M(X_i)$
is equivariantly formal for any
![]() $i$
, Lemma 11.5 (and the remarks preceding it) implies that
$i$
, Lemma 11.5 (and the remarks preceding it) implies that
![]() $M(Y)$
is equivariantly formal. Hence
$M(Y)$
is equivariantly formal. Hence
![]() $Y$
is maximal by Proposition 2.3.
$Y$
is maximal by Proposition 2.3.
Remark 11.8 (Hodge expressivity). Maximality as well as its strengthening Hodge expressivity (see [Reference Brugallé and SchaffhauserBS22]) are notions in terms of realizations (Hodge numbers, Betti numbers of real loci, etc.), and it is clear that the tensor product of two maximal (respectively, Hodge expressive) motives is again maximal (respectively, Hodge expressive). However, it is unclear if a submotive of a maximal or Hodge expressive motive inherits the same property. Hence, a priori, we do not have the Hodge expressive analogue of Corollary 11.7.
11.4 Applications
Despite the formal nature of Corollary 11.7, many results obtained in the previous sections on various constructions of maximal real algebraic varieties can be viewed as instances of Corollary 11.7. Let us list them again by providing either an alternative motivic proof using Corollary 11.7, a motivic explanation of the proof or a conjectural motivic strengthening, in light of Corollary 11.7. Notation is retained from the statements in the previous sections and, in the motivic results, the base field
![]() $\mathbb {R}$
can often be replaced by any field.
$\mathbb {R}$
can often be replaced by any field.
-
(i) (Projective bundle). Proposition 3.3 can be proved directly by using the projective bundle formula for motives, which holds even integrally for Chow motives ([Reference AndréAnd04, §4.3.2]):
Similarly, the claim in Remark 3.4 on flag bundles follows from the flag bundle formula for motives, \begin{align*}\mathfrak {h}(\mathbb {P}_X(E))\simeq \mathfrak {h}(X)\oplus \mathfrak {h}(X)(-1)\oplus \cdots \oplus \mathfrak {h}(X)(-r) \quad \quad \text { in } \textrm {CHM}(\mathbb {R}).\end{align*}
\begin{align*}\mathfrak {h}(\mathbb {P}_X(E))\simeq \mathfrak {h}(X)\oplus \mathfrak {h}(X)(-1)\oplus \cdots \oplus \mathfrak {h}(X)(-r) \quad \quad \text { in } \textrm {CHM}(\mathbb {R}).\end{align*}
 \begin{align*}\mathfrak {h}(\operatorname {Fl}_X(E))\simeq \mathfrak {h}(X)\otimes \mathfrak {h}(\operatorname {Fl(\mathbb {A}^{r+1})}).\end{align*}
\begin{align*}\mathfrak {h}(\operatorname {Fl}_X(E))\simeq \mathfrak {h}(X)\otimes \mathfrak {h}(\operatorname {Fl(\mathbb {A}^{r+1})}).\end{align*}
-
(ii) (Blow-up). Proposition 3.5 can be seen directly by using the blow-up formula for motives, which also holds integrally for Chow motives ([[Reference AndréAnd04], §4.3.2]):
 \begin{align*}\mathfrak {h}(\textrm {Bl}_YX)\simeq \mathfrak {h}(X)\oplus \mathfrak {h}(Y)(-1)\oplus \cdots \oplus \mathfrak {h}(Y)(-(c-1)) \quad \quad \text { in } \textrm {CHM}(\mathbb {R}).\end{align*}
\begin{align*}\mathfrak {h}(\textrm {Bl}_YX)\simeq \mathfrak {h}(X)\oplus \mathfrak {h}(Y)(-1)\oplus \cdots \oplus \mathfrak {h}(Y)(-(c-1)) \quad \quad \text { in } \textrm {CHM}(\mathbb {R}).\end{align*}
-
(iii) (Compactification of configuration space). Proposition 3.7 can be deduced from the fact that the Fulton–MacPherson compactification of the configuration space
 $X[n]$
is motivated by
$X[n]$
is motivated by
 $X$
(even integrally for Chow motives).
$X$
(even integrally for Chow motives). -
(iv) (Surjection of odd degree). The proof of Proposition 3.8 actually shows that, for a generically finite surjection of odd degree
 $Y\to X$
,
$Y\to X$
,
 $X$
is motivated (even for Chow motives with
$X$
is motivated (even for Chow motives with
 $\mathbb {F}_2$
-coefficients) by
$\mathbb {F}_2$
-coefficients) by
 $Y$
.
$Y$
. -
(v) (Moduli of vector bundles on curves). For the moduli space
 $M_C(n,d)$
in Theorem5.3, the main ingredient in our proof is Atiyah and Bott’s Theorem5.1, which suggests that the integral Chow motive of
$M_C(n,d)$
in Theorem5.3, the main ingredient in our proof is Atiyah and Bott’s Theorem5.1, which suggests that the integral Chow motive of
 $M_C(n,d)$
might be motivated by
$M_C(n,d)$
might be motivated by
 $C$
and its symmetric powers. It was known to hold with rational coefficients ([Reference del BañodBn01, Theorem 4.5], [Reference BeauvilleBea95], [Reference BüllesB20, Remark 2.2], [Reference Fu, Hoskins and LehalleurFHPL23, Proposition 4.1]). If we could show that the integral Chow motive of
$C$
and its symmetric powers. It was known to hold with rational coefficients ([Reference del BañodBn01, Theorem 4.5], [Reference BeauvilleBea95], [Reference BüllesB20, Remark 2.2], [Reference Fu, Hoskins and LehalleurFHPL23, Proposition 4.1]). If we could show that the integral Chow motive of
 $M_C(n,d)$
is motivated by the symmetric powers of
$M_C(n,d)$
is motivated by the symmetric powers of
 $C$
, then, using Franz’s Theorem3.2, we may get another alternative proof of Theorem5.3.
$C$
, then, using Franz’s Theorem3.2, we may get another alternative proof of Theorem5.3. -
(vi) (Moduli of parabolic bundles). Using the language of motives, Corollary 5.5 can be proved by induction and by saying that [Reference Fu, Hoskins and LehalleurFHPL23, Corollaries 5.16 and 5.19] imply that
 $M_{C, D}^{\alpha }(n, d, \underline {1})$
is motivated by
$M_{C, D}^{\alpha }(n, d, \underline {1})$
is motivated by
 $M_C(n, d)$
and all
$M_C(n, d)$
and all
 $M_{C, D}^{\alpha }(n^{\prime}, d^{\prime}, \underline {1})$
with
$M_{C, D}^{\alpha }(n^{\prime}, d^{\prime}, \underline {1})$
with
 $(n^{\prime}, d^{\prime}, \underline {1})$
smaller invariants.
$(n^{\prime}, d^{\prime}, \underline {1})$
smaller invariants. -
(vii) (Moduli of Higgs bundles on curves). The main ingredient in the proof of Theorem6.3 for the maximality of the moduli space
 $H_C(n, d)$
is Theorem6.1 (a variant of Markman’s result [Reference MarkmanMar07]). One can expect that
$H_C(n, d)$
is Theorem6.1 (a variant of Markman’s result [Reference MarkmanMar07]). One can expect that
 $H_C(n, d)$
is motivated by all symmetric powers of
$H_C(n, d)$
is motivated by all symmetric powers of
 $C$
. This is only established with rational coefficients in [Reference Hoskins and LehalleurHPL21, Theorem 4.1].
$C$
. This is only established with rational coefficients in [Reference Hoskins and LehalleurHPL21, Theorem 4.1]. -
(viii) (Hilbert square and cube). In Theorem7.3, we actually showed that
 $X^{[2,3]}$
and
$X^{[2,3]}$
and
 $X^{[3]}$
are motivated (for Chow motives with
$X^{[3]}$
are motivated (for Chow motives with
 $\mathbb {F}_2$
-coefficients) by
$\mathbb {F}_2$
-coefficients) by
 $X^{[2]}$
and
$X^{[2]}$
and
 $X$
.
$X$
. -
(ix) (Cubic 3-folds). Theorem7.5 can be proven directly by using the fact that, for a cubic threefolds
 $X$
, its Hilbert square
$X$
, its Hilbert square
 $X^{[2]}$
is motivated by
$X^{[2]}$
is motivated by
 $X$
and its Fano surface of lines
$X$
and its Fano surface of lines
 $F(X)$
, thanks to [Reference Belmans, Fu and RaedscheldersBFR22, Corollary 18].
$F(X)$
, thanks to [Reference Belmans, Fu and RaedscheldersBFR22, Corollary 18]. -
(x) (Hilbert schemes of surfaces). For
 $S^{[n]}$
, the key ingredient towards Theorem8.1 is Li and Qin’s Theorem8.4, which leads to the challenge of understanding the motive of
$S^{[n]}$
, the key ingredient towards Theorem8.1 is Li and Qin’s Theorem8.4, which leads to the challenge of understanding the motive of
 $S^{[n]}$
in terms of the motive of
$S^{[n]}$
in terms of the motive of
 $S$
. The author has no idea for integral coefficients. But with rational coefficients, de Cataldo and Migliorini [Reference de Cataldo and MigliorinidCM02] showed that
$S$
. The author has no idea for integral coefficients. But with rational coefficients, de Cataldo and Migliorini [Reference de Cataldo and MigliorinidCM02] showed that
 $S^{[n]}$
is motivated by
$S^{[n]}$
is motivated by
 $S$
.
$S$
. -
(xi) (Moduli of sheaves on
 $\mathbb {P}^2$
). Ellingsrud and Strømme [Reference Ellingsrud and StrømmeES93] actually show that the Chow motive of
$\mathbb {P}^2$
). Ellingsrud and Strømme [Reference Ellingsrud and StrømmeES93] actually show that the Chow motive of
 $M(r, c_1, c_2)$
is a direct sum of Tate motives in
$M(r, c_1, c_2)$
is a direct sum of Tate motives in
 $\textrm {CHM}(\mathbb {R})$
, from which Theorem9.1 can be immediately deduced, by Corollary 11.7.
$\textrm {CHM}(\mathbb {R})$
, from which Theorem9.1 can be immediately deduced, by Corollary 11.7. -
(xii) (Moduli of sheaves on Poisson surfaces). In view of the result of Markman [Reference MarkmanMar07], we would like to make the following conjecture, with the hope of having more cases than in Theorem10.1.
Conjecture 11.9. The integral Chow motive of
 $M_H(S, v)$
, the moduli space of stable sheaves on a Poisson surface
$M_H(S, v)$
, the moduli space of stable sheaves on a Poisson surface
 $S$
with primitive Mukai vector
$S$
with primitive Mukai vector
 $v$
and
$v$
and
 $v$
-generic stability condition
$v$
-generic stability condition
 $H$
, is in the tensor category generated by the motives of Hilbert schemes
$H$
, is in the tensor category generated by the motives of Hilbert schemes
 $\{S^{[n]}\}_n$
.
$\{S^{[n]}\}_n$
.This conjecture is known with rational coefficients, thanks to Bülles [Reference BüllesB20].
To further illustrate the power of this motivic point of view, we provide some more applications. Firstly, we have the following complement to Theorem8.1.
Theorem 11.10 (Hilbert schemes of surfaces with Tate motives). Let
![]() $S$
be a smooth projective real surface. If its integral Chow motive
$S$
be a smooth projective real surface. If its integral Chow motive
![]() $\mathfrak {h}(S)\in \textrm {CHM}(\mathbb {R})$
is a direct sum of Tate motives, then the Hilbert scheme
$\mathfrak {h}(S)\in \textrm {CHM}(\mathbb {R})$
is a direct sum of Tate motives, then the Hilbert scheme
![]() $S^{[n]}$
is maximal for any
$S^{[n]}$
is maximal for any
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
Proof.
By Totaro [Reference TotaroTot20, Theorem 4.1],
![]() $\mathfrak {h}(S^{[n]})$
is also a direct sum of Tate motives. Since Tate motives are equivariantly formal,
$\mathfrak {h}(S^{[n]})$
is also a direct sum of Tate motives. Since Tate motives are equivariantly formal,
![]() $S^{[n]}$
is maximal.
$S^{[n]}$
is maximal.
Remark 11.11. The above theorem generalizes Corollary 8.6, since
![]() $\mathbb {R}$
-rational real surfaces all have Tate motives. This can be seen from the minimal model theory for real surfaces, the classification of rational real surfaces and the blow-up formula (see the proof of Lemma 4.5).
$\mathbb {R}$
-rational real surfaces all have Tate motives. This can be seen from the minimal model theory for real surfaces, the classification of rational real surfaces and the blow-up formula (see the proof of Lemma 4.5).
Secondly, in the direction of [Reference Kharlamov and RăsdeaconuKR23], we show that cubic 4-folds provide more examples of maximal varieties with non-maximal Hilbert square. This contrasts with the case of cubic 3-folds in Theorem7.5.
Theorem 11.12 (Hilbert squares of cubic 4-folds). Let
![]() $X$
be a real smooth cubic 4-fold. Assume that in Finashin and Kharlamov’s classification [Reference Finashin and KharlamovFK08]
$X$
be a real smooth cubic 4-fold. Assume that in Finashin and Kharlamov’s classification [Reference Finashin and KharlamovFK08]
![]() $X$
does not belong to the regular class corresponding to K3 surfaces with 10 spheres as real locus. Then the Hilbert square
$X$
does not belong to the regular class corresponding to K3 surfaces with 10 spheres as real locus. Then the Hilbert square
![]() $X^{[2]}$
is not maximal. In particular, the Hilbert square of a maximal smooth real cubic 4-fold is not maximal.
$X^{[2]}$
is not maximal. In particular, the Hilbert square of a maximal smooth real cubic 4-fold is not maximal.
Proof.
In [Reference Kharlamov and RăsdeaconuKR23, Theorem 7.7] it is shown that, for such a cubic 4-fold
![]() $X$
, the Fano variety of lines
$X$
, the Fano variety of lines
![]() $F(X)$
is not maximal. However, by the motivic Galkin–Shinder relation established in [Reference Belmans, Fu and RaedscheldersBFR22, Corollary 18],
$F(X)$
is not maximal. However, by the motivic Galkin–Shinder relation established in [Reference Belmans, Fu and RaedscheldersBFR22, Corollary 18],
![]() $F(X)$
is motivated by
$F(X)$
is motivated by
![]() $X^{[2]}$
. Therefore, Corollary 11.7 implies that
$X^{[2]}$
. Therefore, Corollary 11.7 implies that
![]() $X^{[2]}$
cannot be maximal. Finally, note that a maximal cubic 4-fold does not belong to the regular class corresponding to real K3 surfaces with 10 spheres as real locus.
$X^{[2]}$
cannot be maximal. Finally, note that a maximal cubic 4-fold does not belong to the regular class corresponding to real K3 surfaces with 10 spheres as real locus.
Acknowledgements
I would like to express my gratitude to Olivier Benoist, Erwan Brugallé, Victoria Hoskins, Simon Pepin Lehalleur, Burt Totaro and Jean-Yves Welschinger for their interest and invaluable comments on this work. I also extend special thanks to Viatcheslav Kharlamov for his enthusiastic participation in numerous discussions and for generously sharing his recent findings in [Reference Kharlamov and RăsdeaconuKR23]. Furthermore, I am grateful for the conference ‘Real Aspects of Geometry’ held at CIRM in 2022, which provided me with many sources of inspiration. Finally, I want to thank the referee for his or her very helpful comments.
Financial Support
The author is supported by the University of Strasbourg Institute for Advanced Study (USIAS) and by the Agence Nationale de la Recherche (ANR), under project number ANR-20-CE40-0023.
Conflicts of Interest
None.
Journal Information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest
![]() $100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.
$100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.