Consider a generic data unit of random size L that needs to be transmitted over a channel of unit capacity. The channel availability dynamic is modeled as an independent and identically distributed sequence {A, Ai}i≥1 that is independent of L. During each period of time that the channel becomes available, say Ai, we attempt to transmit the data unit. If L <Ai, the transmission is considered successful; otherwise, we wait for the next available period Ai+1 and attempt to retransmit the data from the beginning. We investigate the asymptotic properties of the number of retransmissions N and the total transmission time T until the data is successfully transmitted. In the context of studying the completion times in systems with failures where jobs restart from the beginning, it was first recognized by Fiorini, Sheahan and Lipsky (2005) and Sheahan, Lipsky, Fiorini and Asmussen (2006) that this model results in power-law and, in general, heavy-tailed delays. The main objective of this paper is to uncover the detailed structure of this class of heavy-tailed distributions induced by retransmissions. More precisely, we study how the functional relationship ℙ[L>x]-1 ≈ Φ (ℙ[A>x]-1) impacts the distributions of N and T; the approximation ‘≈’ will be appropriately defined in the paper based on the context. Depending on the growth rate of Φ(·), we discover several criticality points that separate classes of different functional behaviors of the distribution of N. For example, we show that if log(Φ(n)) is slowly varying then log(1/ℙ[N>n]) is essentially slowly varying as well. Interestingly, if log(Φ(n)) grows slower than e√(logn) then we have the asymptotic equivalence log(ℙ[N>n]) ≈ - log(Φ(n)). However, if log(Φ(n)) grows faster than e√(logn), this asymptotic equivalence does not hold and admits a different functional form. Similarly, different types of distributional behavior are shown for moderately heavy tails (Weibull distributions) where log(ℙ[N>n]) ≈ -(log Φ(n))1/(β+1), assuming that log Φ(n) ≈ nβ, as well as the nearly exponential ones of the form log(ℙ[N>n]) ≈ -n/(log n)1/γ, γ>0, when Φ(·) grows faster than two exponential scales log log (Φ(n)) ≈ nγ.

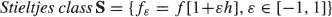 , where
, where 