Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T22:11:14.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Stieltjes classes for moment-indeterminate probability distributions

Part of: Integral transforms, operational calculus Distribution theory - Probability

Published online by Cambridge University Press:  14 July 2016

Jordan Stoyanov
Jordan Stoyanov*
Affiliation:
School of Mathematics and Statistics, University of Newcastle upon Tyne, Newcastle upon Tyne NE1 7RU, UK. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

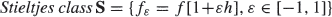Let F be a probability distribution function with density f. We assume that (a) F has finite moments of any integer positive order and (b) the classical problem of moments for F has a nonunique solution (F is M-indeterminate). Our goal is to describe a , where h is a ‘small' perturbation function. Such a class S consists of different distributions Fε (fε is the density of Fε) all sharing the same moments as those of F, thus illustrating the nonuniqueness of F, and of any Fε, in terms of the moments. Power transformations of distributions such as the normal, log-normal and exponential are considered and for them Stieltjes classes written explicitly. We define a characteristic of S called an index of dissimilarity and calculate its value in some cases. A new Stieltjes class involving a power of the normal distribution is presented. An open question about the inverse Gaussian distribution is formulated. Related topics are briefly discussed.

Keywords

Problem of momentsStieltjes class of distributionsindex of dissimilaritynormal distributionlog-normal distributionexponential distributioninverse Gaussian distribution

MSC classification

Primary: 60E05: Distributions 44A60: Moment problems
Type
Part 5. Properties of random variables
Information
Journal of Applied Probability , Volume 41 , Issue A: Stochastic Methods and their Applications , 2004 , pp. 281 - 294
Copyright
Copyright © Applied Probability Trust 2004 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhiezer, N. I. (1965). The Classical Moment Problem and Some Related Questions in Analysis. Oliver and Boyd, Edinburgh.Google Scholar
Berg, C. (1988). The cube of a normal distribution is indeterminate. Ann. Prob. 16, 910–913.Google Scholar
Berg, C. (1995). Indeterminate moment problems and the theory of entire functions. J. Comput. Appl. Math. 65, 27–55.Google Scholar
Berg, C. (1996). Moment problems and polynomial approximation. Ann. Fac. Sci. Toulouse Math. (6) Special issue, 9–32.Google Scholar
Berg, C. (1998). From discrete to absolutely continuous solutions of indeterminate moment problems. Arab J. Math. Sci. 4, 1–18.Google Scholar
Berg, C. (2000). On infinitely divisible solutions to indeterminate moment problems. In Special Functions (Proc. Internat. Workshop, Hong Kong, June 1999), eds Dunkl, C., Ismail, M. and Wong, R., World Scientific, Singapore, pp. 31–41.Google Scholar
Berg, C. and Christensen, J. P. R. (1981). Density questions in the classical theory of moments. Ann. Inst. Fourier (Grenoble) 31, 99–114.Google Scholar
Berg, C. and Valent, G. (1994). The Nevanlinna parametrization for some indeterminate Stieltjes moment problems associated with birth and death processes. Methods Appl. Anal. 1, 169–209.Google Scholar
Bertoin, J., Biane, P. and Yor, M. (2003). Poissonian exponential functionals, q-series, q-integrals, and the moment problem for log-normal distributions. To appear in Stochastic Analysis, Random Fields and Applications IV (Proc. 4th Conf., Ascona, May 2002), eds Dalang, R., Dozzi, M. and Russo, F., Birkhäuser, Basel.Google Scholar
Bingham, N., Goldie, C. and Teugels, J. (1989). Regular Variation (Encyclopedia Math. Appl. 27). Cambridge University Press.Google Scholar
Bondesson, L. (1992). Generalized Gamma Convolutions and Related Classes of Distributions and Densities (Lecture Notes Statist. 76). Springer, New York.CrossRefGoogle Scholar
Bondesson, L. (2002). On the Lévy measure of the log-normal and the logCauchy distributions. Methodol. Comput. Appl. Prob. 4, 243–256.Google Scholar
Diaconis, P. (1987). Application of the method of moments in probability and statistics. In Moments in Mathematics (Proc. Symp. Appl. Math. 37), American Mathematical Society, Providence, RI, pp. 125–142.Google Scholar
Feller, W. (1971). An Introduction to Probability Theory and Its Applications , Vol. 2, 2nd edn. John Wiley, New York.Google Scholar
Gaddum, J. H. (1945). Lognormal distribution. Nature 156, 463–466.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M. (2000). Table of Integrals, Series and Products , 6th edn. Academic Press, New York.Google Scholar
Gut, A. (2002). On the moment problem. Bernoulli 8, 407–421.Google Scholar
Heyde, C. C. (1963a). On a property of the log-normal distribution. J. R. Statist. Soc. B 25, 392–393.Google Scholar
Heyde, C. C. (1963b). Some remarks on the moment problem. I. Quart. J. Math. Oxford 14, 91–96.Google Scholar
Heyde, C. C. (1963C). Some remarks on the moment problem. II. Quart. J. Math. Oxford 14, 97–105.Google Scholar
Heyde, C. C. (1975). Kurtosis and departure from normality. In Statistical Distributions in Scientific Work , Vol. 1, eds Patil, G. P. et al., Reidel, Dordrecht, pp. 193–221.Google Scholar
Hoffmann-Jorgensen, J. (1994). Probability With a View Toward Statistics , Vol. 1. Chapman and Hall, London.Google Scholar
Kjeldsen, T. (1993). The early history of the moment problem. Historia Math. 20, 19–44.Google Scholar
Leipnik, R. (1981). The lognormal distribution and strong nonuniqueness of the moment problem. Theory Prob. Appl. 26, 850–852.CrossRefGoogle Scholar
Lin, G. D. (1997). On the moment problems. Statist. Prob. Lett. 35, 85–90. (Correction: 50 (2000), 205.) Google Scholar
Lin, G. D. and Huang, J. S. (1997). The cube of the logistic distribution is indeterminate. Austral. J. Statist. 39, 247–252.Google Scholar
Lin, G. D. and Stoyanov, J. (2002). On the moment determinacy of the distributions of compound geometric sums. J. Appl. Prob. 39, 545–554.CrossRefGoogle Scholar
McGraw, R., Nemesure, S. and Schwarts, S. E. (1998). Properties and evolution of aerosols with size distributions having identical moments. J. Aerosol Sci. 29, 761–772.Google Scholar
Pakes, A. G. (1996). Length-biasing and laws equivalent to the log-normal. J. Math. Anal. Appl. 191, 825–854.Google Scholar
Pakes, A. G. (2001). Remarks on converse Carleman and Krein criteria for the classical moment problem. J. Austral. Math. Soc. 71, 81–104.Google Scholar
Pares, A. G. and Khattree, R. (1992). Length-biasing, characterizations of laws and the moment problem. Austral. J. Statist. 34, 307–322.Google Scholar
Pares, A. G., Hung, W.-L. and Wu, J.-W. (2001). Criteria for the unique determination of probability distributions by moments. Austral. N. Z. J. Statist. 43, 101–111.Google Scholar
Pedersen, H. L. (1998). On Krein's theorem for indeterminacy of the classical moment problem. J. Approximation Theory 95, 90–100.Google Scholar
Prohorov, Yu. V. and Rozanov, Yu. A. (1969). Probability Theory. Springer, Berlin.CrossRefGoogle Scholar
Rachev, S. T. (1992). Probability Metrics and the Stability of Stochastic Models. John Wiley, Chichester.Google Scholar
Shohat, J. and Tamarkin, J. D. (1943). The Problem of Moments. American Mathematical Society, New York.Google Scholar
Slud, E. (1993). The moment problem for polynomial forms in normal variables. Ann. Prob. 21, 2200–2214.Google Scholar
Stieltjes, T. J. (1894). Recherches sur les fractions continues. Ann. Fac. Sci. Univ. Toulouse 8, J1–J122 and 9, A5-A47. Reprinted in: Ann. Fac. Sci. Toulouse (6) 4 (1995), J1-J122, A5-A47.Google Scholar
Stoyanov, J. (1997). Counterexamples in Probability , 2nd edn. John Wiley, Chichester.Google Scholar
Stoyanov, J. (1999). Inverse Gaussian distribution and the moment problem. J. Appl. Statist. Sci. 9, 61–71.Google Scholar
Stoyanov, J. (2000). Krein condition in probabilistic moment problems. Bernoulli 6, 939–949.Google Scholar
Stoyanov, J. (2002). Moment problems related to the solutions of stochastic differential equations. In Stochastic Theory and Control (Lecture Notes Control Inf. Sci. 280), Springer, Berlin, pp. 459–469.Google Scholar
Stoyanov, J. and Tolmatz, L. (2003). New Stieltjes classes involving generalized gamma distributions. Submitted.Google Scholar
Targhetta, M. L. (1990). On a family of indeterminate distributions. J. Math. Anal. Appl. 147, 477–479.Google Scholar
Thorin, O. (1977). On the infinite divisibility of the lognormal distribution. Scand. Actuarial J. 1977, 121–148.Google Scholar
White, W. H. (1990). Particle size distributions that cannot be distinguished by their moments. J. Colloid Interface Sci. 135, 297–299.Google Scholar