Let X be a smooth projective variety over a finite field 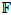 . We discuss the unramified cohomology group H3nr(X, ℚ/ℤ(2)). Several conjectures put together imply that this group is finite. For certain classes of threefolds, H3nr(X, ℚ/ℤ(2)) actually vanishes. It is an open question whether this holds for arbitrary threefolds. For a threefold X equipped with a fibration onto a curve C, the generic fibre of which is a smooth projective surface V over the global field
. We discuss the unramified cohomology group H3nr(X, ℚ/ℤ(2)). Several conjectures put together imply that this group is finite. For certain classes of threefolds, H3nr(X, ℚ/ℤ(2)) actually vanishes. It is an open question whether this holds for arbitrary threefolds. For a threefold X equipped with a fibration onto a curve C, the generic fibre of which is a smooth projective surface V over the global field 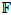 (C), the vanishing of H3nr(X, ℚ/ℤ(2)) together with the Tate conjecture for divisors on X implies a local-global principle of Brauer–Manin type for the Chow group of zero-cycles on V. This sheds new light on work started thirty years ago.
(C), the vanishing of H3nr(X, ℚ/ℤ(2)) together with the Tate conjecture for divisors on X implies a local-global principle of Brauer–Manin type for the Chow group of zero-cycles on V. This sheds new light on work started thirty years ago.

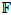 . We discuss the unramified cohomology group
. We discuss the unramified cohomology group 