Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T18:13:03.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Cycles de codimension 2 et H3 non ramifié pour les variétés sur les corps finis

Published online by Cambridge University Press:  04 February 2013

Jean-Louis Colliot-Thélène  and
Bruno Kahn
Jean-Louis Colliot-Thélène
Affiliation:
C.N.R.S., Université Paris Sud, UMR 8628, Mathématiques, Bâtiment 425, 91405 Orsay [email protected]
Bruno Kahn
Affiliation:
Institut de Mathématiques de Jussieu, UMR 7586, Case 247, 4 place Jussieu, 75252 Paris Cedex 05, [email protected]
Get access

Abstract

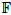Let X be a smooth projective variety over a finite field . We discuss the unramified cohomology group H3nr(X, ℚ/ℤ(2)). Several conjectures put together imply that this group is finite. For certain classes of threefolds, H3nr(X, ℚ/ℤ(2)) actually vanishes. It is an open question whether this holds for arbitrary threefolds. For a threefold X equipped with a fibration onto a curve C, the generic fibre of which is a smooth projective surface V over the global field 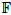(C), the vanishing of H3nr(X, ℚ/ℤ(2)) together with the Tate conjecture for divisors on X implies a local-global principle of Brauer–Manin type for the Chow group of zero-cycles on V. This sheds new light on work started thirty years ago.

Keywords

unramified cohomologyalgebraic cyclesfinite fieldslocalglobal principle19E1514G1514G2514C2514C35
Type
Research Article
Information
Journal of K-Theory , Volume 11 , Issue 1 , February 2013 , pp. 1 - 53
Copyright
Copyright © ISOPP 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Références

1.Bloch, S., On the Chow groups of certain rational surfaces, Ann. Sci. Éc. Norm. Supér. (4) 14 (1981), no. 1, 41–59.CrossRefGoogle Scholar
2.Bloch, S., Lectures on algebraic cycles, Duke University Mathematics Series IV (1980). Second edition : Lectures on Algebraic Cycles : New Mathematical Monographs Series 16, Cambridge University Press (2011).Google Scholar
3.Bloch, S., Ogus, A., Gersten's conjecture and the homology of schemes, Ann. Sci. Éc. Norm. Supér. 7 (1974), 181–201.Google Scholar
4.Bloch, S., Srinivas, V., Remarks on correspondences and algebraic cycles, Amer. J. Math. 105 (1983), 1235–1253.Google Scholar
5.Bourqui, D., Fonction zêta des hauteurs des variétés toriques non déployées. Mem. Amer. Math. Soc. 211 (2011), no. 994.Google Scholar
6.Colliot-Thélène, J.-L., Hilbert's theorem 90 for K 2, with application to the Chow groups of rational surfaces, Invent. math. 71 (1983), 1–20.Google Scholar
7.Colliot-Thélène, J.-L., Cycles algébriques de torsion et K-théorie algébrique, in Arithmetic Algebraic Geometry (CIME, Trento, 1991), Springer L.N.M. 1553 (1993), 1–49.Google Scholar
8.Colliot-Thélène, J.-L., Birational invariants, purity and the Gersten conjecture, in KTheory and Algebraic Geometry : Connections with Quadratic Forms and Division Algebras, AMS Summer Research Institute, Santa Barbara 1992, ed. Jacob, W. and Rosenberg, A., Proceedings of Symposia in Pure Mathematics 58, Part I (1995), 1–64.Google Scholar
9.Colliot-Thélène, J.-L., Conjectures de type local-global sur les groupes de Chow dans la cohomologie étale, in Algebraic K-Theory (1997), Raskind, W. and Weibel, C. ed., Proceedings of Symposia in Pure Mathematics 67, Amer. Math. Soc. (1999), 1–12.Google Scholar
10.Colliot-Thélène, J.-L., Groupe de Chow des zéro-cycles sur les variétés p-adiques ['après Saito, S., K. Sato et al.], Séminaire Bourbaki, 62ème année, 2009–2010, no. 1012.Google Scholar
11.Colliot-Thélène, J.-L., Quelques cas d'annulation du troisième groupe de cohomologie non ramifiée, in Regulators (Barcelone 2010). Contemporary Mathematics 571 (2012), 45–50, Amer. Math. Soc.CrossRefGoogle Scholar
12.Colliot-Thélène, J.-L., Hoobler, R. T. et Kahn, B., The Bloch–Ogus–Gabber theorem, in Algebraic K-theory (Toronto, ON, 1996) (V. P. Snaith ed.), 31–94, Fields Inst. Commun. 16, Amer. Math. Soc., Providence, RI, 1997.Google Scholar
13.Colliot-Thélène, J.-L. et Ojanguren, M., Variétés unirationnelles non rationnelles : audelà de l'exemple d'Artin et Mumford, Invent. math. 97 (1989), 141–158.Google Scholar
14.Colliot-Thélène, J.-L. et Raskind, W., K 2-cohomology and the second Chow group, Math. Ann. 270 (1985), 165–199.Google Scholar
15.Colliot-Thélène, J.-L. et Raskind, W., On the reciprocity law for surfaces over finite fields. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 33 (1986), 283–294.Google Scholar
16.Colliot-Thélène, J.-L. et Sansuc, J.-J., On the Chow groups of certain rational surfaces : a sequel to a paper of S. Bloch. Duke Math. J. 48 (1981), 421–447.Google Scholar
17.Colliot-Thélène, J.-L., Sansuc, J.-J. et Soulé, C., Torsion dans le groupe de Chow de codimension deux, Duke Math. J. 50 (1983), 763–801.CrossRefGoogle Scholar
18.Colliot-Thélène, J.-L. et Szamuely, T., Autour de la conjecture de Tate à coefficients ℤl pour les variétés sur les corps finis, in The Geometry of Algebraic Cycles, ed. Akhtar, R., Brosnan, P., Joshua, R., Clay Mathematics Proceedings 9, Amer. Math. Soc. (2010), 83– 98.Google Scholar
19.Colliot-Thélène, J.-L. et SirSwinnerton-Dyer, Peter, Hasse principle and weak approximation for pencils of Severi–Brauer and similar varieties, Journal für die reine und angew. Math. (Crelle) 453 (1994), 49–112.Google Scholar
20.Colliot-Thélène, J.-L. et Voisin, C., Cohomologie non ramifiée et conjecture de Hodge entière, Duke Math. J. 161 (5) (2012), 735–801.Google Scholar
21.Déglise, F., Transferts sur les groupes de Chow à coefficients, Math. Z. 252 (2006), 315–343.Google Scholar
22.Deligne, P., La conjecture de Weil, I, Pub. Math. IHÉS 43 (1974), 273–307.CrossRefGoogle Scholar
23.Gabber, O., Sur la torsion dans la cohomologie l-adique d'une variété, C. R. Acad. Sci. Paris 297 (1983), 179–182.Google Scholar
24.Geisser, T. et Levine, M., The K-theory of fields in characteristic p, Invent. math. 139 (2000), 459–493.Google Scholar
25.Geisser, T. et Levine, M., The Bloch-Kato conjecture and a theorem of Suslin– Voevodsky, Journal für die reine und angew. Math. (Crelle) 530 (2001), 55–103.Google Scholar
26.Gros, M., Sur la partie p-primaire du groupe de Chow de codimension deux, Comm. Algebra 13 (1985), 2407–2420.Google Scholar
27.Gros, M., Classes de Chern et classes de cycles en cohomologie de Hodge-Witt logarithmique, Mém. SMF 21 (1985), 1–87.Google Scholar
28.Gros, M. et Suwa, N., Application d'Abel-Jacobi p-adique et cycles algébriques, Duke Math. J. 57 (1988), 579–613.Google Scholar
29.Grothendieck, A., La théorie des classes de Chern, Bulletin de la Société Mathématique de France 86 (1958), 137–154.Google Scholar
30.Grothendieck, A., Le groupe de Brauer, II : Théorie cohomologique, in Dix exposés sur la cohomologie des schémas, North Holland, 1968.Google Scholar
31.Grothendieck, A., Le groupe de Brauer, III : exemples et compléments, in Dix exposés sur la cohomologie des schémas, North Holland, 1968.Google Scholar
32.Grothendieck, A., La classe de cohomologie associée à un cycle (réd. P. Deligne), in Cohomologie étale (SGA 4 1/2), Lect. Notes in Math. 569, Springer, 1977, 129–153.Google Scholar
33.Hartshorne, R., Residues and duality, Lect. Notes in Math. 20, Springer, 1966.Google Scholar
34.Illusie, L. et Raynaud, M., Les suites spectrales associées au complexe de de Rham–Witt, Publ. math. I.H.É.S. 57 (1983), 73–212.Google Scholar
35.Jannsen, U. et Sujatha, R., Levels of function fields of surfaces over number fields, J. Algebra 251 (2002), no. 1, 350–357.CrossRefGoogle Scholar
36.Kahn, B., Descente galoisienne et K 2 des corps de nombres, K-theory 7 (1993), 55–100.CrossRefGoogle Scholar
37.Kahn, B., Applications of weight two motivic cohomology, Documenta Mathematica 1 (1996), 395–416.Google Scholar
38.Kahn, B., Équivalence rationnelle, équivalence numérique et produits de courbes elliptiques sur un corps fini, version préliminaire de [39], arXiv:math/0205158.Google Scholar
39.Kahn, B., Équivalences rationnelle et numérique sur certaines variétés de type abélien sur un corps fini, Ann. Sci. Éc. Norm. Supér. 36 (2003), 977–1002.CrossRefGoogle Scholar
40.Kahn, B., Algebraic K-theory, algebraic cycles and arithmetic geometry, in Handbook of K-theory, Vol. 1, Springer, 2005.Google Scholar
41.Kahn, B., Zeta functions and motives, Pure Appl. Math. Quarterly 5 (2009), 507–570 [2008].Google Scholar
42.Kahn, B., Classes de cycles motiviques étales, arXiv:1102.0375v2[math.AG], à paraître dans Algebra & Number Theory.Google Scholar
43.Kahn, B. et Sujatha, R., Birational motives, I : pure birational motives, arXiv:0902. 4902v1[math.AG].CrossRefGoogle Scholar
44.Kato, K., A Hasse principle for two-dimensional global fields, J. für die reine und angew. Math. (Crelle) 366 (1986), 142–181.Google Scholar
45.Kato, K. et Saito, S., Global class field theory of arithmetic schemes, in Applications of Algebraic K-Theory to Algebraic Geometry and Number Theory, Contemporary Math. 55 (I) (1985), 255–331.Google Scholar
46.Kato, K. et Saito, S., Unramified class field theory of arithmetical surfaces, Annals of Math. 118 (1985), 241–275.Google Scholar
47.Katsura, T., Shioda, T., On Fermat varieties, Tôhoku Math. J. 31 (1979), 97–115.Google Scholar
48.Lichtenbaum, S., Values of zeta-functions at non-negative integers, in Number Theory (Noordwijkerhout 1983), Lect. Notes in Math. 1068, 127–138, Springer, 1984.Google Scholar
49.Lichtenbaum, S., The construction of weight-two arithmetic cohomology, Invent. math. 88 (1987), 183–215.Google Scholar
50.Lichtenbaum, S., New results on weight-two arithmetic cohomology, in Grothendieck Festschrift, vol. III, Progress in math. 88 (1990), 35–55.Google Scholar
51.Mazza, C., Voevodsky, V. et Weibel, C., Lecture notes on motivic cohomology, Clay Mathematics Monographs, vol. 2.Google Scholar
52.Merkurjev, A., Rational correspondences, preprint Feb. 2001, disponible sur http://www.math.ucla.edu/∼merkurev/publicat.htm, voir aussi l'appendice RC dans l'article ‘On standard norm varieties’, par Merkurjev, A. S. et Karpenko, N., à paraître dans Ann. Sci. Éc. Norm. Supér.Google Scholar
53.Merkurjev, A. S. et Suslin, A. A., Le groupe K 3 d'un corps, Izv. Akad. Nauk SSSR 54 (1990), 339–356 (trad. anglaise : Math. USSR Izvestija 36 (1990), 541–565).Google Scholar
54.Merkurjev, A. S. et Tignol, J.-P., Galois cohomology of biquadratic extensions. Comment. Math. Helv. 68 (1993), no. 1, 138–169.Google Scholar
55.Milne, J.S., Values of zeta functions of varieties over finite fields, Amer. J. Math. 108 (1986), 297–360.Google Scholar
56.Milne, J.S., Motives over finite fields, in Motives (Seattle, 1991) (Jannsen, U., Kleiman, S., Serre, J.-P. eds.), Proc. Symp. pure Math. 55 (1), Amer. Math. Soc., 1994, 401–459.Google Scholar
57.Milne, J.S., Arithmetic Duality Theorems, Second Edition, Kea Books, 2006.Google Scholar
58.Parimala, R. et Suresh, V., Degree three cohomology of function fields of surfaces, arXiv:1012.5367v1[math.NT], revised version 11th May 2012.Google Scholar
59.Pirutka, A., Sur le groupe de Chow de codimension deux des variétés sur les corps finis, Algebra & Number Theory 5 (6) (2011), 803–817.CrossRefGoogle Scholar
60.Pirutka, A., Cohomologie non ramifiée en degré trois d'une variété de Severi–Brauer, C. R. Acad. Sci. Paris Sér. I 349 (2011), 369–373.Google Scholar
61.Pirutka, A., Invariants birationnels dans la suite spectrale de Bloch–Ogus, arXiv: 1106.3001v1[math.AG], à paraître dans J. K-Theory.Google Scholar
62.Poonen, B., Bertini theorems over finite fields, Annals of Math. 160 (2004), 1099–1127.Google Scholar
63.Rost, M., Chow groups with coefficients, Doc. Math. 1 (1996), 319–393.Google Scholar
64.Saito, S., A global duality theorem for varieties over global fields, in Algebraic K-theory : connections with geometry and topology (Lake Louise, AB, 1987), 425–444, NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 279, Kluwer Acad. Publ., Dordrecht, 1989.Google Scholar
65.Saito, S., Some observations on motivic cohomology of arithmetic schemes, Invent. math. 98 (1989), 371–404.Google Scholar
66.Saito, S. et Sato, K., A p-adic regulator map and finiteness results for arithmetic schemes, Documenta math. Extra Volume Suslin (2010), 525–594.Google Scholar
67.Saito, S. et Sato, K., A finiteness theorem for zero-cycles over -adic fields, with an appendix by Jannsen, U., Annals of Math. 172 (2010), 593–639.Google Scholar
68.Salberger, P., Zero-cycles on rational surfaces over number fields. Invent. math. 91 (1988), 505–524.Google Scholar
69.Salberger, P., On obstructions to the Hasse principle. in Number theory and algebraic geometry, London Math. Soc. Lecture Note Ser. 303, 251–277, Cambridge Univ. Press, Cambridge, 2003.Google Scholar
70.Schoen, C., An integral analog of the Tate conjecture for one-dimensional cycles on varieties over finite fields, Math. Ann. 311 (1998), 493–500.CrossRefGoogle Scholar
71.Scholl, A., Classical motives, in Motives (Seattle, 1991) (Jannsen, U., Kleiman, S., Serre, J.-P., eds.), Proc. Symp. pure Math. 55 (1), Amer. Math. Soc., 1994, 163–187.Google Scholar
72.Spaltenstein, N., Resolutions of unbounded complexes, Compositio Math. 65 (1988), 121–154.Google Scholar
73.Spieß, M., Proof of the Tate conjecture for products of elliptic curves over finite fields, Math. Ann. 314 (1999), 285–290.Google Scholar
74.Suslin, A. A., Quaternion homomorphism for the field of functions on a conic. Dokl. Akad. Nauk SSSR 265 (1982), 292–296. Engl. transl. : Soviet Math. Dokl. 26 (1982), 72–77 (1983).Google Scholar
75.Suslin, A. A. et Voevodsky, V., Bloch-Kato conjecture and motivic cohomology with finite coeffiicients, in The arithmetic and geometry of algebraic cycles (Banff, AB, 1998), 117–189, NATO Sci. Ser. C Math. Phys. Sci., 548, Kluwer Acad. Publ., Dordrecht, 2000.Google Scholar
76.Suwa, N., A note on Gersten's conjecture for logarithmic Hodge-Witt sheaves, K-Theory 9 (1995), 245–271.Google Scholar
77.Tate, J., Endomorphisms of abelian varieties over finite fields, Invent. math. 2 (1966), 134–144.Google Scholar
78.Tate, J., The cohomology groups of tori in finite Galois extensions of number fields, Nagoya Math. J. 27 (1966), 709–719.Google Scholar
79.Tate, J., Conjectures on algebraic cycles in l-adic cohomology, in Motives, (Seattle, 1991) (Jannsen, U., Kleiman, S., Serre, J-P. eds.), Proc. Symposia Pure Math. 55 (1), AMS, 1994, 71–83.Google Scholar
80.Voisin, C., On integral Hodge classes on uniruled and Calabi-Yau threefolds, in Moduli Spaces and Arithmetic Geometry, Advanced Studies in Pure Mathematics 45, 2006, 43–73.Google Scholar
81.Wittenberg, O., Zéro-cycles sur les fibrations au-dessus d'une courbe de genre quelconque, Duke Math. J. 61 (11) (2012), 2113–2166.Google Scholar
82.Zarhin, Yuri G., Poincaré duality and unimodularity, arXiv:1112.1429v3[math. AG].Google Scholar