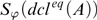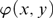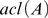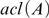2 results
GROUPES FINS
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 12 December 2014, pp. 1120-1132
- Print publication:
- December 2014
-
- Article
- Export citation
Fields with few types
-
- Journal:
- The Journal of Symbolic Logic / Volume 78 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 12 March 2014, pp. 72-84
- Print publication:
- March 2013
-
- Article
- Export citation