Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T01:34:05.818Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUPES FINS

Published online by Cambridge University Press:  12 December 2014

CÉDRIC MILLIET
CÉDRIC MILLIET*
Affiliation:
GALATASARAY ÜNIVERSITESI FEN EDEBIYAT FAKÜLTESI MATEMATIK BÖLÜMÜ ÇIRAĞAN CADDESI N. 36 34357 ORTAKÖY, İSTANBUL, TURKEY
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate some common points between stable structures and weakly small structures and define a structure M to be fine if the Cantor-Bendixson rank of the topological space 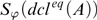${S_\varphi }\left( {dc{l^{eq}}\left( A \right)} \right)$ is an ordinal for every finite subset A of M and every formula 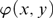$\varphi \left( {x,y} \right)$ where x is of arity 1. By definition, a theory is fine if all its models are so. Stable theories and small theories are fine, and weakly minimal structures are fine. For any finite subset A of a fine group G, the traces on the algebraic closure 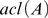$acl\left( A \right)$ of A of definable subgroups of G over 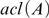$acl\left( A \right)$ which are boolean combinations of instances of an arbitrary fixed formula can decrease only finitely many times. An infinite field with a fine theory has no additive nor multiplicative proper definable subgroups of finite index, nor Artin-Schreier extensions.

Keywords

03C4503C60Model theoryCantor-Bendixson ranklocal descending chain conditionArtin-Schreier extension
Type
Articles
Information
The Journal of Symbolic Logic , Volume 79 , Issue 4 , December 2014 , pp. 1120 - 1132
Copyright
Copyright © The Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Berline, Chantal and Lascar, Daniel, Superstable groups. Annals of Pure and Applied Logic, vol. 30 (1986), pp. 1–43.CrossRefGoogle Scholar
Baldwin, John and Saxl, Jan, Logical stability in group theory. Journal of the Australian Mathematical Society, vol. 21 (1976), pp. 267–276.CrossRefGoogle Scholar
Cherlin, Gregory and Shelah, Saharon, Superstable fields and groups. Annals of Mathematical Logic, vol. 18 (1980), pp. 227–270.Google Scholar
Hrushovski, Ehud, Contributions to stable model theory, Ph.D. thesis, Berkeley, 1986.Google Scholar
Kaplan, Itay, Scanlon, Thomas, and Wagner, Frank O., Artin-Schreier extensions in dependent and simple fields. Israel Journal of Mathematics, vol. 185 (2011), pp. 141–153.Google Scholar
Milliet, Cédric, Small skew fields. Mathematical Logic Quarterly, vol. 53 (2007), pp. 86–90.Google Scholar
Milliet, Cédric, Stable division rings, this Journal, vol. 76 (2011), pp. 348–352.Google Scholar
Milliet, Cédric, On enveloping type-definable structures, this Journal, vol. 76 (2011), pp. 1023–1034.Google Scholar
Milliet, Cédric, On properties of (wealkly) small groups, this Journal, vol. 77 (2012), pp. 94–110.Google Scholar
Milliet, Cédric, Fields and rings with few types, this Journal, vol. 78 (2013), pp. 72–84.Google Scholar
Poizat, Bruno, Groupes stables, Nur Al-Mantiq Wal-Ma’rifah, Villeurbanne, France, 1987.Google Scholar
Poizat, Bruno, Quelques tentatives de définir une notion générale de groupes et de corps de dimension un et de déterminer leurs propriétés algébriques. Confluentes Mathematici, vol. 1 (2009), pp. 111–122.CrossRefGoogle Scholar
Poizat, Bruno and Wagner, Frank O., Sous-groupes périodiques d’un groupe stable, this Journal, vol. 58 (1993), pp. 385–400.Google Scholar
Scanlon, Thomas, Infinite stable fields are Artin-Schreier closed, math.berkeley.edu/∼scanlon/papers/ASclos.pdf, non publié, 1999.Google Scholar
Wagner, Frank O., Small stable groups and generics, this Journal, vol. 56 (1991), pp. 1036–1037.Google Scholar
Wagner, Frank O., Quasi-endomorphisms in small stable groups, this Journal, vol. 58 (1993), pp. 1044–1051.Google Scholar
Wagner, Frank O., Small fields, this Journal, vol. 63 (1998), pp. 995–1002.Google Scholar
Wood, Carol, Notes on stability of separably closed fields, this Journal, vol. 44 (1979), pp. 337–352.Google Scholar