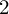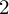5 results
DEFORMATIONS OF THE VERONESE EMBEDDING AND FINSLER
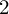 $2$
-SPHERES OF CONSTANT CURVATURE
$2$
-SPHERES OF CONSTANT CURVATURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 2103-2134
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
SFT COMPUTATIONS AND INTERSECTION THEORY IN HIGHER-DIMENSIONAL CONTACT MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1219-1270
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Lecture 1 - Closed Holomorphic Curves in Symplectic 4-Manifolds
-
- Book:
- Lectures on Contact 3-Manifolds, Holomorphic Curves and Intersection Theory
- Published online:
- 06 March 2020
- Print publication:
- 26 March 2020, pp 11-25
-
- Chapter
- Export citation
Introduction: Motivation
-
- Book:
- Lectures on Contact 3-Manifolds, Holomorphic Curves and Intersection Theory
- Published online:
- 06 March 2020
- Print publication:
- 26 March 2020, pp 1-10
-
- Chapter
- Export citation

Lectures on Contact 3-Manifolds, Holomorphic Curves and Intersection Theory
-
- Published online:
- 06 March 2020
- Print publication:
- 26 March 2020