Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T10:50:47.361Z Has data issue: false hasContentIssue false
  • English
  • Français

SFT COMPUTATIONS AND INTERSECTION THEORY IN HIGHER-DIMENSIONAL CONTACT MANIFOLDS

Part of: Symplectic geometry, contact geometry

Published online by Cambridge University Press:  25 January 2021

Agustin Moreno Open the ORCID record for Agustin Moreno [Opens in a new window]
Agustin Moreno*
Affiliation:
Uppsala Universitet, Uppsala, Sweden
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

I construct infinitely many nondiffeomorphic examples of 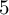$5$ -dimensional contact manifolds which are tight, admit no strong fillings and do not have Giroux torsion. I obtain obstruction results for symplectic cobordisms, for which I give a proof not relying on the polyfold abstract perturbation scheme for Symplectic Field Theory (SFT). These results are part of my PhD thesis [23], and are the first applications of higher-dimensional Siefring intersection theory for holomorphic curves and hypersurfaces, as outlined in [23, 24], as a prequel to [30].

Keywords

Contact TopologySymplectic GeometryHolomorphic CurvesSymplectic Field Theory

MSC classification

Primary: 53D42: Symplectic field theory; contact homology
Secondary: 53D10: Contact manifolds, general 53D35: Global theory of symplectic and contact manifolds
Type
Review Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 4 , July 2022 , pp. 1219 - 1270
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Bourgeois, F., A Morse–Bott approach to contact homology, Fields Inst. Commun. 35 (2003), 55–77.Google Scholar
Chas, M. and Sullivan, D., String topology, Preprint, 1999, arXiv:math/9911159.Google Scholar
Cieliebak, K., Nonlinear functional analysis, lecture notes, https://www.math.uni-augsburg.de/prof/geo/Books-and-Scripts/nonlin_10_.pdf.Google Scholar
Cieliebak, K. and Latschev, J., The role of string topology in symplectic field theory, in New Perspectives and Challenges in Symplectic Field Theory, CRM Proc. Lect. Notes 49 (Providence, American Mathematical Society, 2009), 113–146.Google Scholar
Eliashberg, Y., Givental, A. and Hofer, H., Introduction to symplectic field theory, Geom. Funct. Anal. special volume (2000), 560–673.Google Scholar
Hofer, H., Wysocki, K. and Zehnder, E., Integration theory on the zero sets of polyfold Fredholm sections, Math. Ann. 346(1) (2010), 139–198.CrossRefGoogle Scholar
Hutchings, M., A magic trick for defining obstruction bundles, http://floerhomology.wordpress.com/2013/09/04/.Google Scholar
Hutchings, M., Gluing a flow line to itself, https://floerhomology.wordpress.com/2014/07/14/gluing-a-flow-line-to-itself/.Google Scholar
Hutchings, M. and Gerig, C., Obstruction bundle gluing, notes for IHES Moduli Conference July 2015, https://www.math.ias.edu/~joelfish/Hutchings_full.pdf.Google Scholar
Hutchings, M. and Taubes, C., Gluing pseudoholomorphic curves along branched covered cylinders: I, J. Symplectic Geom. 5(1) (2007), 43–137.CrossRefGoogle Scholar
Hutchings, M. and Taubes, C., Gluing pseudoholomorphic curves along branched covered cylinders: II, J. Symplectic Geom. 7(1) (2009), 29–133.CrossRefGoogle Scholar
Kutluhan, C., Matic, G., Van Horn-Morris, J. and Wand, A., Algebraic torsion via Heegaard Floer homology, Preprint, 2015, arXiv:1503.01685v3.Google Scholar
Latschev, J. and Wendl, C., Algebraic torsion in contact manifolds, Geom. Funct. Anal. 21(5) (2011), 1144–1195.CrossRefGoogle Scholar
Lisi, S., Van Horn-Morris, J. and Wendl, C., On symplectic fillings of spinal open book decompositions I: Geometric constructions, Preprint, 2018, arXiv:1810.12017.Google Scholar
Lutz, R., Structures de contact sur les fibrès principaux en cercles de dimension trois, Ann. Inst. Fourier (Grenoble) 27(3) (1977), ix, 1–15 (French, with English summary).CrossRefGoogle Scholar
Massot, P., Niederkrüger, K. and Wendl, C., Weak and strong fillability of higher dimensional contact manifolds, Inv. Math. 192(2) (2013), 287–373.CrossRefGoogle Scholar
McDuff, D., Symplectic manifolds with contact type boundaries, Inv. Math. 103(1) (1991), 651–671.CrossRefGoogle Scholar
Moreno, A., Algebraic and Giroux torsion in higher-dimensional contact manifolds, Preprint.Google Scholar
Moreno, A., Algebraic Torsion in Higher-Dimensional Contact Manifolds , PhD thesis, Humboldt Universität zu Berlin, 2018, arXiv:1711.01562.Google Scholar
Moreno, A. and Siefring, R., Holomorphic curves in the presence of holomorphic hypersurface foliations, Preprint, 2019, arXiv:1902.02700.Google Scholar
Mori, A., Reeb foliations on ${S}^5$ and contact $5$ –manifolds violating the Thurston-Bennequin inequality, Preprint, 2009, arXiv:0906.3237.Google Scholar
Niederkrüger, K. and Wendl, C., Weak symplectic fillings and holomorphic curves, Ann. Sci. Éc. Norm. Supér. (4) 44(5) (2011), 801–853.CrossRefGoogle Scholar
Schoenfeld, E., Higher Symplectic Field Theory Invariants for Cotangent Bundles of Surfaces , PhD thesis, Stanford University.Google Scholar
Siefring, R., Intersection theory of punctured pseudoholomorphic curves, Geom. Topol. 15(4) (2011), 2351–2457.CrossRefGoogle Scholar
Siefring, R., Finite-energy pseudoholomorphic planes with multiple asymptotic limits, Math. Ann. 368(1-2) (2017), 367–390.CrossRefGoogle Scholar
Siefring, R., Symplectic field theory and stable hamiltonian submanifolds: Intersection theory, In preparation.Google Scholar
Thurston, W., Some simple examples of symplectic manifolds, Proc. Amer. Math. Soc. 55 (1976), 467–468.Google Scholar
Wendl, C., Automatic transversality and orbifolds of punctured holomorphic curves in dimension four, Comment. Math. Helv. 85(2) (2010), 347–407.CrossRefGoogle Scholar
Wendl, C., Lectures on symplectic field theory, Lecture notes, arXiv:1612.01009v2.Google Scholar
Wendl, C., A hierarchy of local symplectic filling obstructions for contact 3-manifolds, Duke Math. J. 162(12) (2013), 2197–2283.CrossRefGoogle Scholar
Wendl, C., Strongly fillable contact manifolds and $J$ -holomorphic foliations, Duke Math. J. 151(3) (2010), 337–384.Google Scholar
Wendl, C., Transversality and super-rigidity for multiply covered holomorphic curves, Preprint, 2016, arXiv:1609.09867.Google Scholar
Wendl, C., Contact 3-manifolds, holomorphic curves and intersection theory, Lecture notes, arXiv:1706.05540.Google Scholar
Wendl, C., Super-rigidity is fixed, https://symplecticfieldtheorist.wordpress.com/2019/05/27/super-rigidity-is-fixed/.Google Scholar
Wendl, C., Lectures on Holomorphic Curves in Symplectic and Contact Geometry, https://www.mathematik.hu-berlin.de/∼wendl/pub/jhol_bookv33.pdf.Google Scholar