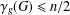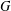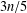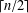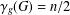4 results
Applications of Combinatorial Programming to Data Analysis: The Traveling Salesman and Related Problems
-
- Journal:
- Psychometrika / Volume 43 / Issue 1 / March 1978
- Published online by Cambridge University Press:
- 01 January 2025, pp. 81-91
-
- Article
- Export citation
Assessing the computational complexity of multilayer subgraph detection
-
- Journal:
- Network Science / Volume 7 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 05 August 2019, pp. 215-241
-
- Article
- Export citation
THE DOMINATION GAME ON SPLIT GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 327-337
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
On Spanning and Dominating Circuits in Graphs
-
- Journal:
- Canadian Mathematical Bulletin / Volume 20 / Issue 2 / 01 June 1977
- Published online by Cambridge University Press:
- 20 November 2018, pp. 215-220
- Print publication:
- 01 June 1977
-
- Article
-
- You have access
- Export citation