Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T19:09:06.775Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DOMINATION GAME ON SPLIT GRAPHS

Part of: Game theory Graph theory

Published online by Cambridge University Press:  12 November 2018

TIJO JAMES ,
SANDI KLAVŽAR Open the ORCID record for SANDI KLAVŽAR [Opens in a new window]  and
AMBAT VIJAYAKUMAR
TIJO JAMES
Affiliation:
Department of Mathematics, Pavanatma College, Murickassery, India Department of Mathematics, Cochin University of Science and Technology, India email [email protected]
SANDI KLAVŽAR*
Affiliation:
Faculty of Mathematics and Physics, University of Ljubljana, Slovenia Faculty of Natural Sciences and Mathematics, University of Maribor, Slovenia Institute of Mathematics, Physics and Mechanics, Ljubljana, Slovenia email [email protected]
AMBAT VIJAYAKUMAR
Affiliation:
Department of Mathematics, Cochin University of Science and Technology, India email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

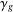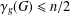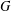We investigate the domination game and the game domination number $\unicode[STIX]{x1D6FE}_{g}$ in the class of split graphs. We prove that $\unicode[STIX]{x1D6FE}_{g}(G)\leq n/2$ for any isolate-free $n$-vertex split graph $G$, thus strengthening the conjectured 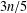$3n/5$ general bound and supporting Rall’s 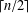$\lceil n/2\rceil$-conjecture. We also characterise split graphs of even order with 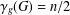$\unicode[STIX]{x1D6FE}_{g}(G)=n/2$.

Keywords

domination gamesplit graphHamiltonian path

MSC classification

Primary: 91A43: Games involving graphs
Secondary: 05C57: Games on graphs 05C69: Dominating sets, independent sets, cliques
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 2 , April 2019 , pp. 327 - 337
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The second author acknowledges the financial support from the Slovenian Research Agency (research core funding No. P1-0297 and the project N1-0043 Combinatorial Problems with an Emphasis on Games).

References

Brešar, B., Dorbec, P., Klavžar, S. and Košmrlj, G., ‘How long can one bluff in the domination game?’, Discuss. Math. Graph Theory 37 (2017), 337–352.Google Scholar
Brešar, B., Klavžar, S., Košmrlj, G. and Rall, D. F., ‘Domination game: extremal families of graphs for the 3/5-conjectures’, Discrete Appl. Math. 161 (2013), 1308–1316.Google Scholar
Brešar, B., Klavžar, S. and Rall, D. F., ‘Domination game and an imagination strategy’, SIAM J. Discrete Math. 24 (2010), 979–991.Google Scholar
Brešar, B. and Movarraei, N., ‘On the number of maximal independent sets in minimum colorings of split graphs’, Discrete Appl. Math. 247 (2018), 352–356.Google Scholar
Bujtás, C., ‘Domination game on forests’, Discrete Math. 338 (2015), 2220–2228.Google Scholar
Bujtás, C., ‘On the game total domination number’, Graphs Combin. 34 (2018), 415–425.Google Scholar
Bujtás, C., Henning, M. A. and Tuza, Z., ‘Transversal game on hypergraphs and the [[()[]mml:mfrac[]()]][[()[]mml:mrow []()]]3[[()[]/mml:mrow[]()]] [[()[]mml:mrow []()]]4[[()[]/mml:mrow[]()]][[()[]/mml:mfrac[]()]]-conjecture on the total domination game’, SIAM J. Discrete Math. 30 (2016), 1830–1847.10.1137/15M1049361Google Scholar
Chen, G., Ellingham, M. N., Saito, A. and Shan, S., ‘Spanning trails with maximum degree at most 4 in 2K 2 -free graphs’, Graphs Combin. 33 (2017), 1095–1101.Google Scholar
Chung, F. R. K., Gyárfás, A., Tuza, Z. and Trotter, W. T., ‘The maximum number of edges in 2K 2 -free graphs of bounded degree’, Discrete Math. 81 (1990), 129–135.Google Scholar
Collins, K. L. and Trenk, A. N., ‘Finding balance: split graphs and related classes’, Electron. J. Combin. 25 (2018), Paper 1.73, 14 pp.Google Scholar
Dorbec, P., Košmrlj, G. and Renault, G., ‘The domination game played on unions of graphs’, Discrete Math. 338 (2015), 71–79.Google Scholar
Foldes, S. and Hammer, P. L., ‘Split graphs’, in: Proc. Eighth Southeastern Conf. Combinatorics, Graph Theory and Computing, Congressus Numerantium, XIX (Utilitas Mathematica, Winnipeg, Manitoba, 1977), 311–315.Google Scholar
Henning, M. A. and Kinnersley, W. B., ‘Domination game: a proof of the 3/5-conjecture for graphs with minimum degree at least two’, SIAM J. Discrete Math. 30 (2016), 20–35.Google Scholar
Henning, M. A., Klavžar, S. and Rall, D. F., ‘Total version of the domination game’, Graphs Combin. 31 (2015), 1453–1462.Google Scholar
Henning, M. A., Klavžar, S. and Rall, D. F., ‘The 4/5 upper bound on the game total domination number’, Combinatorica 37 (2017), 223–251.Google Scholar
Henning, M. A. and Löwenstein, C., ‘Domination game: extremal families for the 3/5-conjecture for forests’, Discuss. Math. Graph Theory 37 (2017), 369–381.Google Scholar
Kinnersley, W. B., West, D. B. and Zamani, R., ‘Game domination for grid-like graphs’, Manuscript, 2012.Google Scholar
Kinnersley, W. B., West, D. B. and Zamani, R., ‘Extremal problems for game domination number’, SIAM J. Discrete Math. 27 (2013), 2090–2107.Google Scholar
Košmrlj, G., ‘Domination game on paths and cycles’, Ars Math. Contemp. 13 (2017), 125–136.Google Scholar
Renjith, P. and Sadagopan, N., ‘Hamiltonicity in split graphs – a dichotomy’, in: Conf. Algorithms and Discrete Applied Mathematics, Lecture Notes in Computer Science, 10156 (eds. Gaur, D. and Narayanaswamy, N.) (Springer, Cham, 2017), 320–331.Google Scholar
Sciriha, I., Briffa, J. A. and Debono, M., ‘Fast algorithms for indices of nested split graphs approximating real complex networks’, Discrete Appl. Math. 247 (2018), 152–164.Google Scholar