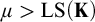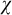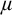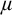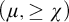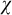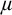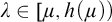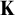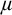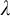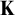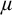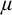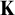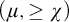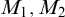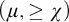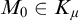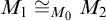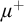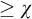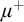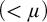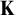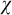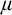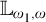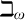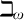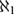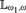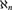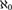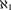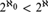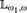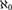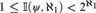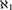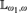Assuming the existence of a monster model, tameness, and continuity of nonsplitting in an abstract elementary class (AEC), we extend known superstability results: let 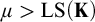 $\mu>\operatorname {LS}(\mathbf {K})$ be a regular stability cardinal and let
$\mu>\operatorname {LS}(\mathbf {K})$ be a regular stability cardinal and let 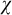 $\chi $ be the local character of
$\chi $ be the local character of 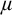 $\mu $-nonsplitting. The following holds:
$\mu $-nonsplitting. The following holds:
1. When 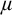 $\mu $-nonforking is restricted to
$\mu $-nonforking is restricted to 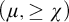 $(\mu ,\geq \chi )$-limit models ordered by universal extensions, it enjoys invariance, monotonicity, uniqueness, existence, extension, and continuity. It also has local character
$(\mu ,\geq \chi )$-limit models ordered by universal extensions, it enjoys invariance, monotonicity, uniqueness, existence, extension, and continuity. It also has local character 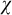 $\chi $. This generalizes Vasey’s result [37, Corollary 13.16] which assumed
$\chi $. This generalizes Vasey’s result [37, Corollary 13.16] which assumed 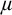 $\mu $-superstability to obtain same properties but with local character
$\mu $-superstability to obtain same properties but with local character 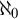 $\aleph _0$.
$\aleph _0$.
2. There is 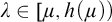 $\lambda \in [\mu ,h(\mu ))$ such that if
$\lambda \in [\mu ,h(\mu ))$ such that if 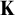 $\mathbf {K}$ is stable in every cardinal between
$\mathbf {K}$ is stable in every cardinal between 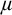 $\mu $ and
$\mu $ and 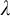 $\lambda $, then
$\lambda $, then 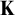 $\mathbf {K}$ has
$\mathbf {K}$ has 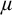 $\mu $-symmetry while
$\mu $-symmetry while 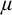 $\mu $-nonforking in (1) has symmetry. In this case:
$\mu $-nonforking in (1) has symmetry. In this case:
(a) 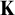 $\mathbf {K}$ has the uniqueness of
$\mathbf {K}$ has the uniqueness of 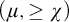 $(\mu ,\geq \chi )$-limit models: if
$(\mu ,\geq \chi )$-limit models: if 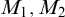 $M_1,M_2$ are both
$M_1,M_2$ are both 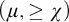 $(\mu ,\geq \chi )$-limit over some
$(\mu ,\geq \chi )$-limit over some 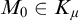 $M_0\in K_{\mu }$, then
$M_0\in K_{\mu }$, then 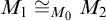 $M_1\cong _{M_0}M_2$;
$M_1\cong _{M_0}M_2$;
(b) any increasing chain of 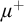 $\mu ^+$-saturated models of length
$\mu ^+$-saturated models of length 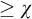 $\geq \chi $ has a
$\geq \chi $ has a 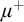 $\mu ^+$-saturated union. These generalize [31] and remove the symmetry assumption in [10, 38] .
$\mu ^+$-saturated union. These generalize [31] and remove the symmetry assumption in [10, 38] .
Under 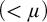 $(<\mu )$-tameness, the conclusions of (1), (2)(a)(b) are equivalent to
$(<\mu )$-tameness, the conclusions of (1), (2)(a)(b) are equivalent to 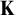 $\mathbf {K}$ having the
$\mathbf {K}$ having the 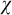 $\chi $-local character of
$\chi $-local character of 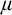 $\mu $-nonsplitting.
$\mu $-nonsplitting.
Grossberg and Vasey [18, 38] gave eventual superstability criteria for tame AECs with a monster model. We remove the high cardinal threshold and reduce the cardinal jump between equivalent superstability criteria. We also add two new superstability criteria to the list: a weaker version of solvability and the boundedness of the U-rank.
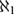 ${\aleph _1}$
${\aleph _1}$