No CrossRef data available.
Published online by Cambridge University Press: 20 July 2020
We investigate, in ZFC, the behavior of abstract elementary classes (AECs) categorical in many successive small cardinals. We prove for example that a universal 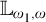 $\mathbb {L}_{\omega _1, \omega }$
sentence categorical on an end segment of cardinals below
$\mathbb {L}_{\omega _1, \omega }$
sentence categorical on an end segment of cardinals below 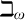 $\beth _\omega $
must be categorical also everywhere above
$\beth _\omega $
must be categorical also everywhere above 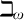 $\beth _\omega $
. This is done without any additional model-theoretic hypotheses (such as amalgamation or arbitrarily large models) and generalizes to the much broader framework of tame AECs with weak amalgamation and coherent sequences.
$\beth _\omega $
. This is done without any additional model-theoretic hypotheses (such as amalgamation or arbitrarily large models) and generalizes to the much broader framework of tame AECs with weak amalgamation and coherent sequences.