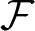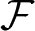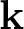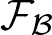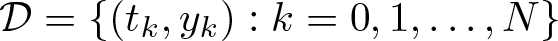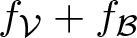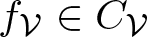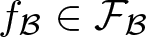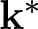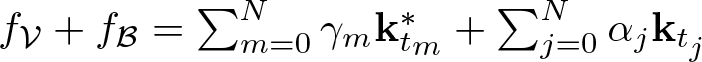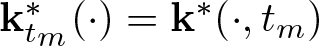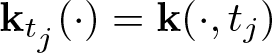In this paper,the linear space 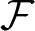$\mathcal F$ of a special type of fractal interpolation functions (FIFs) on an interval I is considered. Each FIF in 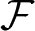$\mathcal F$ is established from a continuous function on I. We show that, for a finite set of linearly independent continuous functions on I, we get linearly independent FIFs. 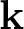Then we study a finite-dimensional reproducing kernel Hilbert space (RKHS) $\mathcal F_{\mathcal B}\subset\mathcal F$, and the reproducing kernel $\mathbf k$ for $\mathcal F_{\mathcal B}$ is defined by a basis of 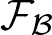$\mathcal F_{\mathcal B}$. For a given data set 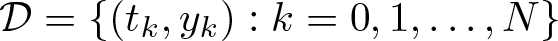$\mathcal D=\{(t_k, y_k) : k=0,1,\ldots,N\}$, we apply our results to curve fitting problems of minimizing the regularized empirical error based on functions of the form 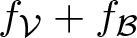$f_{\mathcal V}+f_{\mathcal B}$, where 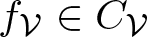$f_{\mathcal V}\in C_{\mathcal V}$ and 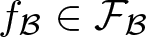$f_{\mathcal B}\in \mathcal F_{\mathcal B}$. Here $C_{\mathcal V}$ is another finite-dimensional RKHS of some classes of regular continuous functions with the reproducing kernel 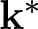$\mathbf k^*$. We show that the solution function can be written in the form 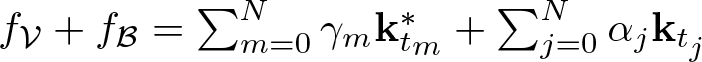$f_{\mathcal V}+f_{\mathcal B}=\sum_{m=0}^N\gamma_m\mathbf k^*_{t_m} +\sum_{j=0}^N \alpha_j\mathbf k_{t_j}$, where 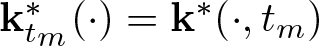${\mathbf k}_{t_m}^\ast(\cdot)={\mathbf k}^\ast(\cdot,t_m)$ and 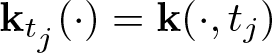$\mathbf k_{t_j}(\cdot)=\mathbf k(\cdot,t_j)$, and the coefficients γm and αj can be solved by a system of linear equations.

We define fractal interpolation on unbounded domains for a certain class of topological spaces and construct local fractal functions. In addition, we derive some properties of these local fractal functions, consider their tensor products, and give conditions for local fractal functions on unbounded domains to be elements of Bochner–Lebesgue spaces.