No CrossRef data available.
Published online by Cambridge University Press: 26 November 2024
In this paper,the linear space 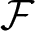 $\mathcal F$ of a special type of fractal interpolation functions (FIFs) on an interval I is considered. Each FIF in
$\mathcal F$ of a special type of fractal interpolation functions (FIFs) on an interval I is considered. Each FIF in 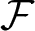 $\mathcal F$ is established from a continuous function on I. We show that, for a finite set of linearly independent continuous functions on I, we get linearly independent FIFs. Then we study a finite-dimensional reproducing kernel Hilbert space (RKHS)
$\mathcal F$ is established from a continuous function on I. We show that, for a finite set of linearly independent continuous functions on I, we get linearly independent FIFs. Then we study a finite-dimensional reproducing kernel Hilbert space (RKHS)  $\mathcal F_{\mathcal B}\subset\mathcal F$, and the reproducing kernel
$\mathcal F_{\mathcal B}\subset\mathcal F$, and the reproducing kernel 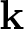 $\mathbf k$ for
$\mathbf k$ for  $\mathcal F_{\mathcal B}$ is defined by a basis of
$\mathcal F_{\mathcal B}$ is defined by a basis of 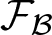 $\mathcal F_{\mathcal B}$. For a given data set
$\mathcal F_{\mathcal B}$. For a given data set 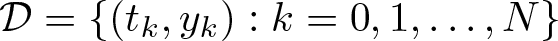 $\mathcal D=\{(t_k, y_k) : k=0,1,\ldots,N\}$, we apply our results to curve fitting problems of minimizing the regularized empirical error based on functions of the form
$\mathcal D=\{(t_k, y_k) : k=0,1,\ldots,N\}$, we apply our results to curve fitting problems of minimizing the regularized empirical error based on functions of the form 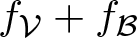 $f_{\mathcal V}+f_{\mathcal B}$, where
$f_{\mathcal V}+f_{\mathcal B}$, where 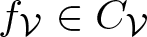 $f_{\mathcal V}\in C_{\mathcal V}$ and
$f_{\mathcal V}\in C_{\mathcal V}$ and 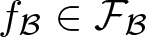 $f_{\mathcal B}\in \mathcal F_{\mathcal B}$. Here
$f_{\mathcal B}\in \mathcal F_{\mathcal B}$. Here  $C_{\mathcal V}$ is another finite-dimensional RKHS of some classes of regular continuous functions with the reproducing kernel
$C_{\mathcal V}$ is another finite-dimensional RKHS of some classes of regular continuous functions with the reproducing kernel 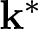 $\mathbf k^*$. We show that the solution function can be written in the form
$\mathbf k^*$. We show that the solution function can be written in the form 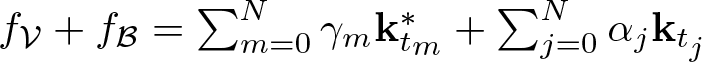 $f_{\mathcal V}+f_{\mathcal B}=\sum_{m=0}^N\gamma_m\mathbf k^*_{t_m} +\sum_{j=0}^N \alpha_j\mathbf k_{t_j}$, where
$f_{\mathcal V}+f_{\mathcal B}=\sum_{m=0}^N\gamma_m\mathbf k^*_{t_m} +\sum_{j=0}^N \alpha_j\mathbf k_{t_j}$, where 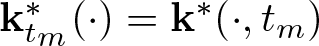 ${\mathbf k}_{t_m}^\ast(\cdot)={\mathbf k}^\ast(\cdot,t_m)$ and
${\mathbf k}_{t_m}^\ast(\cdot)={\mathbf k}^\ast(\cdot,t_m)$ and 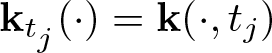 $\mathbf k_{t_j}(\cdot)=\mathbf k(\cdot,t_j)$, and the coefficients γm and αj can be solved by a system of linear equations.
$\mathbf k_{t_j}(\cdot)=\mathbf k(\cdot,t_j)$, and the coefficients γm and αj can be solved by a system of linear equations.