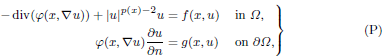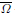2 results
Infinitely many solutions for equations of p(x)-Laplace type with the nonlinear Neumann boundary condition
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 24 August 2017, pp. 1-31
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
-
We investigate the following nonlinear Neumann boundary-value problem with associated p(x)-Laplace-type operator
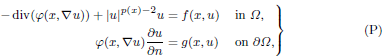
where the function φ(x, v) is of type |v|p(x)−2v with continuous function p: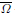
→ (1,∞) and both f : Ω × ℝ → ℝ and g : ∂Ω × ℝ → ℝ satisfy a Carathéodory condition. We first show the existence of infinitely many weak solutions for the Neumann problems using the Fountain theorem with the Cerami condition but without the Ambrosetti and Rabinowitz condition. Next, we give a result on the existence of a sequence of weak solutions for problem (P) converging to 0 in L∞-norm by employing De Giorgi's iteration and the localization method under suitable conditions.
Qualitative Analysis of Solutions for a Class of Anisotropic Elliptic Equations with Variable Exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 15 December 2015, pp. 541-557
-
- Article
- Export citation
-
We are concerned with the degenerate anisotropic problem
We first establish the existence of an unbounded sequence of weak solutions. We also obtain the existence of a non-trivial weak solution if the nonlinear term f has a special form. The proofs rely on the fountain theorem and Ekeland's variational principle.
