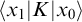We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We start by showing how to approximate unitary and bounded self-adjoint operators by operators in finite dimensional spaces. Using ultraproducts we give a precise meaning for the approximation. In this process we see how the spectral measure is obtained as an ultralimit of counting measures that arise naturally from the finite dimensional approximations. Then we see how generalized distributions can be interpreted in the ultraproduct. Finally we study how one can calculate kernels of operators K by calculating them in the finite dimensional approximations and how one needs to interpret Dirac deltas in the ultraproduct in order to get the kernels as propagators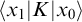 
$\langle x_{1}|K|x_{0}\rangle $.
