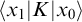1 Introduction
This paper continues a study of finite dimensional approximations of operators on Hilbert spaces. We started the work in [Reference Hirvonen and Hyttinen6], motivated by a quest for mathematically justified eigenvectors in quantum mechanics. There we built eigenvectors directly as ultraproducts of eigenvectors in the small spaces. This time we look at another way of finding finite dimensional approximations, and reconstruct the spectral decomposition theorem using ultraproducts. We also find structure resembling rigged Hilbert spaces, thus providing generalized eigenvectors and bringing us back to our earlier motivation.
In quantum mechanics the states of a system are usually represented by unit vectors in a Hilbert space. Observables of the system are modeled by self-adjoint (often unbounded) operators whose spectrum gives the possible measurement outcomes. If the observable has a finite spectrum and a finite number of eigenvectors, this model coincides with Dirac’s bra- and ket-vector representation [Reference Dirac3], but in general Dirac’s bras and kets don’t form a Hilbert space. A key ingredient in Dirac’s approach, the delta-functions, were later mathematically justified by Schwartz [Reference Schwartz10] as distributions, functionals over a set of test functions. Gelfand and Vilenkin [Reference Gelfand and Ya4] found a natural space for these, namely the rigged Hilbert spaces. These are triplets of spaces: in addition to a Hilbert space, one considers a dense subspace of it—the test functions—and the space of either linear or antilinear functions over these test functions. This last space, in which the Hilbert space embeds naturally, is the space of distributions. The linear functions correspond to bra vectors, the antilinear functions to ket vectors.
One key question about quantum systems is how they evolve over time. Depending on the approach to the system, this is described either by the kernel of the time evolution operator, or via the Feynman propagator. The kernel is a function
![]() $K(x,y)$
such that the action of the time evolution operator K on a wave function
$K(x,y)$
such that the action of the time evolution operator K on a wave function
![]() $\varphi $
can be described by
$\varphi $
can be described by
where S is the spectrum of the observable.
We study a method of calculating the kernel via the finite dimensional approximations. Although our method builds on ultraproducts, the space studied is not the full ultraproduct, but a subspace of it. As this is not elementary, we cannot use Łos’s theorem, but this is not a problem: as we are only interested in equations, it is enough to have just an embedding of the original space into the ultraproduct space. This also means that our approach does not restrict to only pseudocompact spaces (the metric analogue of pseudofinite spaces, see [Reference Goldbring and Lopes5]).
Discrete approximations of quantum systems have been used and studied extensively in physics. From the list of references of [Reference Hirvonen and Hyttinen6] one can find examples of this. They have been studied also in mathematical physics, see, e.g., [Reference Barker1]. We got inspired by the work of B. Zilber [Reference Zilber12], and set out to compute concrete examples of kernels in [Reference Hirvonen and Hyttinen6]. The question we studied there was whether it is possible to calculate the kernels of the time evolution operators by calculating them in some kind of finitely generated approximations of quantum systems which in [Reference Hirvonen and Hyttinen6] were the free particle and the harmonic oscillator. It turned out that in these cases it is possible. One can choose the approximations to be simply finite dimensional Hilbert spaces with rather straightforward approximations of the position operator and the momentum operator. In the choice of the approximations of the time evolution operator one needed to be more creative in the case of the harmonic oscillator. To determine in which sense the approximations approximate the quantum systems was more tricky. For that we used a rather heavily modified version of the metric ultraproduct of the finite dimensional Hilbert spaces. Once we knew how the approximation works, it was rather straightforward to do the calculations with the help of number theory.
However, following Zilber, we would have liked to be able to calculate the kernels by using Dirac deltas in the propagator style
![]() $\langle x_{1}|K|x_{0}\rangle $
. In [Reference Hirvonen and Hyttinen6] our interpretation of Dirac deltas was as ultraproducts of eigenvectors. In hind sight that was too naive an approach, and didn’t work out. The propagators calculated in the finite dimensional models did not give a correct propagator in the ultraproduct, and not even some kind of ad hoc renormalization would have made the values correct, as there were also divisibility-related discretizing effects stemming from the finite approximations. The remedy in [Reference Hirvonen and Hyttinen6] was to calculate the kernel instead, as this could be done using the propagators in the finite dimensional models, and the method ‘averaged out’ the discretization effect.
$\langle x_{1}|K|x_{0}\rangle $
. In [Reference Hirvonen and Hyttinen6] our interpretation of Dirac deltas was as ultraproducts of eigenvectors. In hind sight that was too naive an approach, and didn’t work out. The propagators calculated in the finite dimensional models did not give a correct propagator in the ultraproduct, and not even some kind of ad hoc renormalization would have made the values correct, as there were also divisibility-related discretizing effects stemming from the finite approximations. The remedy in [Reference Hirvonen and Hyttinen6] was to calculate the kernel instead, as this could be done using the propagators in the finite dimensional models, and the method ‘averaged out’ the discretization effect.
In this paper we continue the work we started in [Reference Hirvonen and Hyttinen6], but we look at a general case instead of concrete examples. Also, the method is different. The first question we look at is the following: Given a separable Hilbert space H and an operator A on it, can one find finite dimensional Hilbert spaces
![]() $H_{N}$
and operators
$H_{N}$
and operators
![]() $A_{N}$
on them so that the operators approximate A in the sense that H with A is isometrically isomorphic to a submodel of the metric ultraproduct of the spaces
$A_{N}$
on them so that the operators approximate A in the sense that H with A is isometrically isomorphic to a submodel of the metric ultraproduct of the spaces
![]() $H_{N}$
with operators
$H_{N}$
with operators
![]() $A_{N}$
? The first problem in finding the pairs
$A_{N}$
? The first problem in finding the pairs
![]() $(H_{N},A_{N})$
is that in the case where the operator A is unbounded, the metric ultraproduct
$(H_{N},A_{N})$
is that in the case where the operator A is unbounded, the metric ultraproduct
![]() $A^{m}$
of the operators
$A^{m}$
of the operators
![]() $A_{N}$
can not be well-defined everywhere in the metric ultraproduct
$A_{N}$
can not be well-defined everywhere in the metric ultraproduct
![]() $H^{m}$
of the spaces
$H^{m}$
of the spaces
![]() $H_{N}$
. In [Reference Hirvonen and Hyttinen6] looking at the position and momentum operators, we were able to show that
$H_{N}$
. In [Reference Hirvonen and Hyttinen6] looking at the position and momentum operators, we were able to show that
![]() $A^{m}$
is well defined in a suitable part of
$A^{m}$
is well defined in a suitable part of
![]() $H^{m}$
so that the isomorphism can indeed be found. In this paper we look only at bounded operators and thus this problem does not arise. Although this does restrict the direct applicability of our method, we hope the method can be extended, more on this below.
$H^{m}$
so that the isomorphism can indeed be found. In this paper we look only at bounded operators and thus this problem does not arise. Although this does restrict the direct applicability of our method, we hope the method can be extended, more on this below.
In sections 2 and 3 we consider the approximation question in the case where A is such that
![]() $AA^{*}=A^{*}A=rI$
where r is a positive real and I is the identity operator. So, e.g., A can be a unitary operator. We show how the operators
$AA^{*}=A^{*}A=rI$
where r is a positive real and I is the identity operator. So, e.g., A can be a unitary operator. We show how the operators
![]() $A_{N}$
can be found, show how the spectral measure
$A_{N}$
can be found, show how the spectral measure
![]() $\mu $
for A is obtained as an ultralimit of counting measures that arise from the approximations naturally, and how the approximations give A as a multiplication operator in the space
$\mu $
for A is obtained as an ultralimit of counting measures that arise from the approximations naturally, and how the approximations give A as a multiplication operator in the space
![]() $L_{2}(\sigma (A),\mu )$
.
$L_{2}(\sigma (A),\mu )$
.
In the fouth section we study the same questions for bounded self-adjoint operators A and get the same results by reducing the questions to the previous case by looking at the operator
![]() $e^{irA}$
for r a small enough real.
$e^{irA}$
for r a small enough real.
In the fifth section we look at generalized distributions in the context of the space
![]() $L_{2}(\sigma (A),\mu )$
from the previous sections. See [Reference Reed and Simon9] for the classical theory of generalized distributions. Now the generalized distributions (excluding some) cannot be seen as elements of
$L_{2}(\sigma (A),\mu )$
from the previous sections. See [Reference Reed and Simon9] for the classical theory of generalized distributions. Now the generalized distributions (excluding some) cannot be seen as elements of
![]() $H^{m}$
. Thus we look at the space
$H^{m}$
. Thus we look at the space
![]() $H^{\infty }$
which is obtained from the classical ultraproduct of the spaces
$H^{\infty }$
which is obtained from the classical ultraproduct of the spaces
![]() $H_{N}$
by fractioning out the equivalence relation of being infinitely close to each other in a metric that arises from the norms in
$H_{N}$
by fractioning out the equivalence relation of being infinitely close to each other in a metric that arises from the norms in
![]() $H_N$
. This space contains infinite vectors giving us a chance. The problem here is that the ultraproduct of the inner products in the spaces
$H_N$
. This space contains infinite vectors giving us a chance. The problem here is that the ultraproduct of the inner products in the spaces
![]() $H_{N}$
is not well-defined everywhere in
$H_{N}$
is not well-defined everywhere in
![]() $H^{\infty }\times H^{\infty }$
. It turns out that it is well defined in a large enough subset so that one can interpret generalized distributions
$H^{\infty }\times H^{\infty }$
. It turns out that it is well defined in a large enough subset so that one can interpret generalized distributions
![]() $\theta $
as vectors
$\theta $
as vectors
![]() $u(\theta )$
in
$u(\theta )$
in
![]() $H^{\infty }$
so that for all continuous
$H^{\infty }$
so that for all continuous
![]() $f:\sigma (A)\rightarrow \mathbb {C}$
, where
$f:\sigma (A)\rightarrow \mathbb {C}$
, where
![]() $\mathbb {C}$
is the field of complex numbers,
$\mathbb {C}$
is the field of complex numbers,
![]() $\theta (f)=\langle F^m(f)|u(\theta )\rangle $
where
$\theta (f)=\langle F^m(f)|u(\theta )\rangle $
where
![]() $F^m$
is a natural embedding we get from the isometric embedding of
$F^m$
is a natural embedding we get from the isometric embedding of
![]() $L_{2}(\sigma (A),\mu )$
into
$L_{2}(\sigma (A),\mu )$
into
![]() $H^{m}$
, see above (the embedding is not into
$H^{m}$
, see above (the embedding is not into
![]() $H^{\infty }$
, for details see Section 4).
$H^{\infty }$
, for details see Section 4).
In the sixth section we look at ways of calculating the kernel of an operator B on
![]() $L_{2}(\sigma (A),\mu )$
(or on H). We start by showing that the method from [Reference Hirvonen and Hyttinen6] works also here assuming that we can find reasonable approximations
$L_{2}(\sigma (A),\mu )$
(or on H). We start by showing that the method from [Reference Hirvonen and Hyttinen6] works also here assuming that we can find reasonable approximations
![]() $B_{N}$
for B in the spaces
$B_{N}$
for B in the spaces
![]() $H_{N}$
. In [Reference Hirvonen and Hyttinen6] we showed how to find these for the time evolution operators B of the free particle and the harmonic oscillator (there A was the position operator). Here we show that if B has a kernel, then the reasonable approximations
$H_{N}$
. In [Reference Hirvonen and Hyttinen6] we showed how to find these for the time evolution operators B of the free particle and the harmonic oscillator (there A was the position operator). Here we show that if B has a kernel, then the reasonable approximations
![]() $B_{N}$
can always be found. However, unlike in the special cases studied in [Reference Hirvonen and Hyttinen6], here our proof is essentially existential and does not give a practical way of finding the approximations. One must keep in mind that finding the kernels is difficult and thus one can not expect to have a simple trick that gives them.
$B_{N}$
can always be found. However, unlike in the special cases studied in [Reference Hirvonen and Hyttinen6], here our proof is essentially existential and does not give a practical way of finding the approximations. One must keep in mind that finding the kernels is difficult and thus one can not expect to have a simple trick that gives them.
In the sixth section we also show that the kernel can be obtained as the propagator
![]() $\langle x_{1}|B|x_{0}\rangle $
(using the discrete approximations we can extend B to an operator that acts also on Dirac deltas) if one is very careful in choosing the interpretations of the Dirac deltas
$\langle x_{1}|B|x_{0}\rangle $
(using the discrete approximations we can extend B to an operator that acts also on Dirac deltas) if one is very careful in choosing the interpretations of the Dirac deltas
![]() $|x_{1}\rangle $
and
$|x_{1}\rangle $
and
![]() $|x_{0}\rangle $
and here, of course, we think of Dirac deltas as generalized distributions as is common in mathematics. The need to be very careful comes from the fact that
$|x_{0}\rangle $
and here, of course, we think of Dirac deltas as generalized distributions as is common in mathematics. The need to be very careful comes from the fact that
![]() $\langle x_{1}|B|x_{0}\rangle $
is very sensitive to the choice of eigenvectors, as opposed to
$\langle x_{1}|B|x_{0}\rangle $
is very sensitive to the choice of eigenvectors, as opposed to
![]() $\langle F^m(f)|u(\theta )\rangle $
. In [Reference Hirvonen and Hyttinen6] we showed that a straightforward approach to eigenvectors can give completely wrong values. As the result, this Dirac delta method is probably not very practical if applied in a straightforward manner. From [Reference de la Madrid Modino8] one can find an example of a rigorous use of Dirac deltas in the context where Dirac deltas are interpreted as generalized distributions.
$\langle F^m(f)|u(\theta )\rangle $
. In [Reference Hirvonen and Hyttinen6] we showed that a straightforward approach to eigenvectors can give completely wrong values. As the result, this Dirac delta method is probably not very practical if applied in a straightforward manner. From [Reference de la Madrid Modino8] one can find an example of a rigorous use of Dirac deltas in the context where Dirac deltas are interpreted as generalized distributions.
Open question 1. Can one find approximations
![]() $A_{N}$
for bounded normal operators A or unbounded self adjoint operators?
$A_{N}$
for bounded normal operators A or unbounded self adjoint operators?
Although it is not immediate, we believe that if one can find finite dimensional approximations of bounded normal operators, one can combine the classical trick of looking at the operators
![]() $(A\pm iI)^{-1}$
and our technique for building unbounded operators in ultraproducts from [Reference Hirvonen and Hyttinen6] to find approximations for unbounded self-adjoint operators. However, even in the case of bounded normal operators we have a serious problem: How to find the approximations
$(A\pm iI)^{-1}$
and our technique for building unbounded operators in ultraproducts from [Reference Hirvonen and Hyttinen6] to find approximations for unbounded self-adjoint operators. However, even in the case of bounded normal operators we have a serious problem: How to find the approximations
![]() $A_{N}$
so that they are roughly like how we chose them in Section 1 and still normal. (With the assumption
$A_{N}$
so that they are roughly like how we chose them in Section 1 and still normal. (With the assumption
![]() $AA^{*}=A^{*}A=rI$
, there are no problems in guaranteeing normality, in fact, this assumption was designed to get normal approximations.) The conventional trick of decomposing normal operators into two commuting self-adjoint ones does not seem to work directly, as building approximations for them in the spaces
$AA^{*}=A^{*}A=rI$
, there are no problems in guaranteeing normality, in fact, this assumption was designed to get normal approximations.) The conventional trick of decomposing normal operators into two commuting self-adjoint ones does not seem to work directly, as building approximations for them in the spaces
![]() $H_N$
seems to destroy commutativity. However, our current understanding is that there may be a remedy to this.
$H_N$
seems to destroy commutativity. However, our current understanding is that there may be a remedy to this.
2 The construction
This section presents the basic construction of finite-dimensional approximations that we will use and modify in later sections. Here we study a separable Hilbert space with a (scaled) unitary operator having a cyclic vector. We use the cyclic vector and polynomials to build finite-dimensional approximations such that the original Hilbert space embeds isometrically into their metric ultraproduct. We also get a vector space homomorphism from the space of polynomials (over a compact set
![]() $S\subset \mathbb {C}$
) into the metric ultraproduct. In Section 3 we will construct a suitable measure to make the homomorphism an isometry.
$S\subset \mathbb {C}$
) into the metric ultraproduct. In Section 3 we will construct a suitable measure to make the homomorphism an isometry.
The construction will be used to find similar approximations for the case where the operator is bounded and self-adjoint in Section 4. In Section 5 we will study other norms for the ultraproduct space that will be essential in studying distributions in Sections 5 and 6. In Section 7 we will have a short look at what one can do if the operator doesn’t have a cyclic vector.
So we let H be a separable complex Hilbert space and A an operator on H of the form
![]() $qU$
, where q is a nonzero complex number and U is unitary. Then A is normal and bounded and
$qU$
, where q is a nonzero complex number and U is unitary. Then A is normal and bounded and
![]() $A^{*}\circ A=A\circ A^{*}=r_{A}I$
where
$A^{*}\circ A=A\circ A^{*}=r_{A}I$
where
![]() $r_{A}$
is a positive real, I is the identity operator, and
$r_{A}$
is a positive real, I is the identity operator, and
![]() $A^{*}$
is the adjoint of A. This is enough for the constructions we do in this paper (we will use the construction when A is unitary), but we use notation allowing for more general operators, as there are also other operators allowing for this sort of approximations (see the example at the end of this section).
$A^{*}$
is the adjoint of A. This is enough for the constructions we do in this paper (we will use the construction when A is unitary), but we use notation allowing for more general operators, as there are also other operators allowing for this sort of approximations (see the example at the end of this section).
From a polynomial
![]() $P(X,Y)\in \mathbb {C} [X,Y]$
over the complex numbers
$P(X,Y)\in \mathbb {C} [X,Y]$
over the complex numbers
![]() $\mathbb {C}$
we get an operator
$\mathbb {C}$
we get an operator
![]() $P(A,A^{*})$
on H the natural way, e.g.,
$P(A,A^{*})$
on H the natural way, e.g.,
![]() $X^{2}Y(A,A^{*})=A\circ A\circ A^{*}$
, and we say that
$X^{2}Y(A,A^{*})=A\circ A\circ A^{*}$
, and we say that
![]() $\phi \in H$
is cyclic if the set
$\phi \in H$
is cyclic if the set
![]() $\{ P(A,A^{*})(\phi )\vert \ P\in \mathbb {C} [X,Y]\}$
is dense in H. We will here study the case where there is a cyclic vector
$\{ P(A,A^{*})(\phi )\vert \ P\in \mathbb {C} [X,Y]\}$
is dense in H. We will here study the case where there is a cyclic vector
![]() $\phi $
in H and we pick
$\phi $
in H and we pick
![]() $\phi $
so that in addition its norm is
$\phi $
so that in addition its norm is
![]() $1$
. Notice that H can always be split into countably many complete subspaces so that they are orthogonal to each other, closed under A and
$1$
. Notice that H can always be split into countably many complete subspaces so that they are orthogonal to each other, closed under A and
![]() $A^{*}$
and each of them has a cyclic vector, and in Section 7 we will see how to combine the constructions from this decomposition.
$A^{*}$
and each of them has a cyclic vector, and in Section 7 we will see how to combine the constructions from this decomposition.
For all
![]() $N\in {\omega }$
, let
$N\in {\omega }$
, let
![]() $H_{N}$
be the subspace of H generated by
$H_{N}$
be the subspace of H generated by
In particular, note that
![]() $H_0$
is the space generated by
$H_0$
is the space generated by
![]() $\phi $
, and
$\phi $
, and
![]() $H_N\subset H_{N+1}$
. Notice that as finite dimensional spaces these are complete spaces. We write
$H_N\subset H_{N+1}$
. Notice that as finite dimensional spaces these are complete spaces. We write
![]() $H^{-}_{N}$
for the subspace of H generated by
$H^{-}_{N}$
for the subspace of H generated by
and
![]() $H^{+}_{N}$
for the subspace of H generated by
$H^{+}_{N}$
for the subspace of H generated by
As
![]() $AA^*=A^*A=r_AI$
, the operators A and
$AA^*=A^*A=r_AI$
, the operators A and
![]() $A^*$
swap these spaces: A maps
$A^*$
swap these spaces: A maps
![]() $H^{-}_{N}$
onto
$H^{-}_{N}$
onto
![]() $H^{+}_{N}$
and
$H^{+}_{N}$
and
![]() $A^{*}$
maps
$A^{*}$
maps
![]() $H^{+}_{N}$
onto
$H^{+}_{N}$
onto
![]() $H^{-}_{N}$
. To get approximating operators on
$H^{-}_{N}$
. To get approximating operators on
![]() $H_N$
we can modify A and
$H_N$
we can modify A and
![]() $A^*$
by a wraparound trick: Let
$A^*$
by a wraparound trick: Let
![]() $W^{-}$
be the orthogonal complement of
$W^{-}$
be the orthogonal complement of
![]() $H^{-}_{N}$
in
$H^{-}_{N}$
in
![]() $H_{N}$
and
$H_{N}$
and
![]() $W^{+}$
be the orthogonal complement of
$W^{+}$
be the orthogonal complement of
![]() $H^{+}_{N}$
in
$H^{+}_{N}$
in
![]() $H_{N}$
. Then
$H_{N}$
. Then
![]() $W^{+}$
and
$W^{+}$
and
![]() $W^{-}$
have the same dimension and we let U be a unitary operator from
$W^{-}$
have the same dimension and we let U be a unitary operator from
![]() $W^{-}$
onto
$W^{-}$
onto
![]() $W^{+}$
. Now we define an operator
$W^{+}$
. Now we define an operator
![]() $A_{N}$
on
$A_{N}$
on
![]() $H_{N}$
as follows. If
$H_{N}$
as follows. If
![]() $u\in H^{-}_{N}$
, then
$u\in H^{-}_{N}$
, then
![]() $A_{N}(u)=A(u)$
and if
$A_{N}(u)=A(u)$
and if
![]() $u\in W^{-}$
, then
$u\in W^{-}$
, then
![]() $A_{N}(u)=\sqrt {r_{A}}U(u)$
(by
$A_{N}(u)=\sqrt {r_{A}}U(u)$
(by
![]() $\sqrt {r_{A}}$
we mean the one that is positive). We get the adjoint of
$\sqrt {r_{A}}$
we mean the one that is positive). We get the adjoint of
![]() $A_{N}$
as follows: If
$A_{N}$
as follows: If
![]() $u\in H^{+}_{N}$
, then we let
$u\in H^{+}_{N}$
, then we let
![]() $A^{*}_{N}(u)=A^{*}(u)$
and if
$A^{*}_{N}(u)=A^{*}(u)$
and if
![]() $u\in W^{+}$
, then
$u\in W^{+}$
, then
![]() $A^{*}_{N}(u)=\sqrt {r_{A}}U^{-1}(u)$
. It is easy to check that
$A^{*}_{N}(u)=\sqrt {r_{A}}U^{-1}(u)$
. It is easy to check that
![]() $A^{*}_{N}$
is indeed the adjoint of
$A^{*}_{N}$
is indeed the adjoint of
![]() $A_{N}$
and that
$A_{N}$
and that
![]() $A^{*}_{N}\circ A_{N}=A_{N}\circ A^{*}_{N}=r_{A}I$
and so
$A^{*}_{N}\circ A_{N}=A_{N}\circ A^{*}_{N}=r_{A}I$
and so
![]() $A_{N}$
is normal. Notice that because of how A and
$A_{N}$
is normal. Notice that because of how A and
![]() $A^*$
cancel out (up to multiplication by a constant),
$A^*$
cancel out (up to multiplication by a constant),
![]() $H^{+}_{N}$
is also generated by the set
$H^{+}_{N}$
is also generated by the set
![]() $\{A^{i}(A^{*})^{j}(\phi )\vert \ i\le N,\ j< N\}$
. Thus
$\{A^{i}(A^{*})^{j}(\phi )\vert \ i\le N,\ j< N\}$
. Thus
![]() $H_N^-$
and
$H_N^-$
and
![]() $H_N^+$
are the subspaces on which
$H_N^+$
are the subspaces on which
![]() $A_N$
and
$A_N$
and
![]() $A_N^*$
respectively behave ‘correctly’ and
$A_N^*$
respectively behave ‘correctly’ and
and
In
![]() $H_{N}$
we can also define operators
$H_{N}$
we can also define operators
![]() $P(A_{N},A_{N}^{*})$
for polynomials
$P(A_{N},A_{N}^{*})$
for polynomials
![]() $P(X,Y)$
in the natural way.
$P(X,Y)$
in the natural way.
For all
![]() $N\in {\omega }$
, we let
$N\in {\omega }$
, we let
![]() $D_{N}$
be the dimension of
$D_{N}$
be the dimension of
![]() $H_{N}$
and we choose eigenvectors
$H_{N}$
and we choose eigenvectors
![]() $u_{N}(n)$
,
$u_{N}(n)$
,
![]() $n<D_{N}$
, of
$n<D_{N}$
, of
![]() $A_{N}$
with eigenvalues
$A_{N}$
with eigenvalues
![]() $\lambda _{N}(n)$
. Notice that
$\lambda _{N}(n)$
. Notice that
where
![]() $\overline {\lambda _{N}(n)}$
is the complex conjugate of
$\overline {\lambda _{N}(n)}$
is the complex conjugate of
![]() $\lambda _{N}(n)$
. Since
$\lambda _{N}(n)$
. Since
![]() $A_{N}$
is normal, we can choose these so that they form an orthonormal basis of
$A_{N}$
is normal, we can choose these so that they form an orthonormal basis of
![]() $H_{N}$
. Denote
$H_{N}$
. Denote
![]() $\xi _{N}(n)=\langle u_{N}(n) |\phi \rangle $
, i.e.,
$\xi _{N}(n)=\langle u_{N}(n) |\phi \rangle $
, i.e.,
 $$ \begin{align} \phi =\sum_{n=0}^{D_{N}-1}\xi_{N}(n)u_{N}(n), \end{align} $$
$$ \begin{align} \phi =\sum_{n=0}^{D_{N}-1}\xi_{N}(n)u_{N}(n), \end{align} $$
and we choose the vectors
![]() $u_{N}(n)$
so that in addition
$u_{N}(n)$
so that in addition
![]() $\xi _{N}(n)$
is a non-negative real number. Then we have
$\xi _{N}(n)$
is a non-negative real number. Then we have
 $$ \begin{align} A_N(\phi)=\sum_{n=0}^{D_{N}-1}\lambda_N(n)\xi_{N}(n)u_{N}(n)\ \text{and}\ A^*_N(\phi)=\sum_{n=0}^{D_{N}-1}\overline{\lambda_N(n)}\xi_{N}(n)u_{N}(n). \end{align} $$
$$ \begin{align} A_N(\phi)=\sum_{n=0}^{D_{N}-1}\lambda_N(n)\xi_{N}(n)u_{N}(n)\ \text{and}\ A^*_N(\phi)=\sum_{n=0}^{D_{N}-1}\overline{\lambda_N(n)}\xi_{N}(n)u_{N}(n). \end{align} $$
One should note that even though the spaces
![]() $H_N$
form an increasing sequence, the bases do not extend each other, as the operators
$H_N$
form an increasing sequence, the bases do not extend each other, as the operators
![]() $A_N$
(as well as the operators
$A_N$
(as well as the operators
![]() $A_N^*$
) do not extend each other (because of the wraparound modification).
$A_N^*$
) do not extend each other (because of the wraparound modification).
Next we want to tie a spectral decomposition of A to our finite-dimensional approximation. So we choose a natural number M so that it is strictly greater than both the operator norm of A and
![]() $\sqrt {r_{A}}$
, and let
$\sqrt {r_{A}}$
, and let
Notice that there is a real
![]() $\varepsilon>0$
such that for all
$\varepsilon>0$
such that for all
![]() $N<{\omega }$
and
$N<{\omega }$
and
![]() $n<D_{N}$
,
$n<D_{N}$
,
![]() $\vert \lambda _{N}(n)\vert <M-\varepsilon $
since the norm of
$\vert \lambda _{N}(n)\vert <M-\varepsilon $
since the norm of
![]() $A_{N}$
is at most the maximum of the norm of A and
$A_{N}$
is at most the maximum of the norm of A and
![]() $\sqrt {r_{A}}$
. For all
$\sqrt {r_{A}}$
. For all
![]() $X\subseteq \mathbb {C}$
, let
$X\subseteq \mathbb {C}$
, let
![]() $C(X)$
be the vector space of all bounded continuous functions from X to
$C(X)$
be the vector space of all bounded continuous functions from X to
![]() $\mathbb {C}$
. Of these our main interest is in
$\mathbb {C}$
. Of these our main interest is in
![]() $C(S)$
. Notice that since S is compact, every
$C(S)$
. Notice that since S is compact, every
![]() $f\in C(S)$
is uniformly continuous. We let
$f\in C(S)$
is uniformly continuous. We let
![]() $D(S)$
be the subspace of
$D(S)$
be the subspace of
![]() $C(S)$
that consists of all functions
$C(S)$
that consists of all functions
![]() $f_{P}(\lambda )=P(\lambda ,\overline \lambda )$
, where
$f_{P}(\lambda )=P(\lambda ,\overline \lambda )$
, where
![]() $P\in \mathbb {C}[X,Y]$
and
$P\in \mathbb {C}[X,Y]$
and
![]() $\overline \lambda $
is the complex conjugate of
$\overline \lambda $
is the complex conjugate of
![]() $\lambda $
. On
$\lambda $
. On
![]() $D(S)$
we can again define operators
$D(S)$
we can again define operators
![]() $A_{D}$
and
$A_{D}$
and
![]() $A^{*}_{D}$
in a natural way
$A^{*}_{D}$
in a natural way
(e.g.,
![]() $A_{D}(f_{X^{i}Y^{j}})=f_{X^{i+1}Y^{j}}$
). Notice that
$A_{D}(f_{X^{i}Y^{j}})=f_{X^{i+1}Y^{j}}$
). Notice that
![]() $A_{D}(f_{P})(\lambda )=\lambda f_{P}(\lambda )$
and
$A_{D}(f_{P})(\lambda )=\lambda f_{P}(\lambda )$
and
![]() $A^{*}_{D}(f_{P})(\lambda )=\overline \lambda f_{P}(\lambda )$
.
$A^{*}_{D}(f_{P})(\lambda )=\overline \lambda f_{P}(\lambda )$
.
Let’s define some mappings that will be crucial in this paper:
Definition 2.1. We define
![]() $G: D(S)\to H$
and
$G: D(S)\to H$
and
![]() $F_N:D(S)\to H_N$
as follows: For
$F_N:D(S)\to H_N$
as follows: For
![]() $P\in \mathbb {C}[X,Y]$
, let
$P\in \mathbb {C}[X,Y]$
, let
and note that it is a homomorphism from
![]() $D(S)$
to H (as vector spaces), and that its image is dense in H (by the cyclicity assumption). Further let
$D(S)$
to H (as vector spaces), and that its image is dense in H (by the cyclicity assumption). Further let
and note by comparing to Equation (8) that
![]() $F_{N}(f_{P})=P(A_{N},A_{N}^{*})(\phi )$
, and also that this is a homomorphism from
$F_{N}(f_{P})=P(A_{N},A_{N}^{*})(\phi )$
, and also that this is a homomorphism from
![]() $D(S)$
to
$D(S)$
to
![]() $H_{N}$
. Also note, that as
$H_{N}$
. Also note, that as
![]() $\lVert {A_N}\rVert $
is always bounded by
$\lVert {A_N}\rVert $
is always bounded by
![]() $\max \{\lVert {A}\rVert ,\sqrt {r_A}\}$
, for each
$\max \{\lVert {A}\rVert ,\sqrt {r_A}\}$
, for each
![]() $f_P\in D(S)$
,
$f_P\in D(S)$
,
![]() $\{F_N(f_P):N\geq 1\}$
is bounded.
$\{F_N(f_P):N\geq 1\}$
is bounded.
Now the inner product in
![]() $H_{N}$
(inherited from H), gives us one norm
$H_{N}$
(inherited from H), gives us one norm
![]() $\Vert \cdot \Vert _{2}$
on
$\Vert \cdot \Vert _{2}$
on
![]() $H_{N}$
. Using this, there is a natural way of defining metric ultraproducts of the Hilbert spaces
$H_{N}$
. Using this, there is a natural way of defining metric ultraproducts of the Hilbert spaces
![]() $H_N$
. However, we want to consider also other norms in the ultraproduct, so we take as our starting point a classical ultraproduct of the structures
$H_N$
. However, we want to consider also other norms in the ultraproduct, so we take as our starting point a classical ultraproduct of the structures
![]() $H_N$
and ‘dig out’ various metric ultraproduct spaces from it. We look at the
$H_N$
and ‘dig out’ various metric ultraproduct spaces from it. We look at the
![]() $\lVert {\cdot }\rVert _2$
-norm here, and consider the other norms in Section 5.
$\lVert {\cdot }\rVert _2$
-norm here, and consider the other norms in Section 5.
Let
![]() ${\mathcal {U}}$
be a nonprincipal ultrafilter on
${\mathcal {U}}$
be a nonprincipal ultrafilter on
![]() ${\omega }$
. Depending on what one wishes to calculate using the finite dimensional approximations, here there is room to adjust the ultrafilter accordingly. For example, in [Reference Hirvonen and Hyttinen6] our calculations required that for all
${\omega }$
. Depending on what one wishes to calculate using the finite dimensional approximations, here there is room to adjust the ultrafilter accordingly. For example, in [Reference Hirvonen and Hyttinen6] our calculations required that for all
![]() $m\in {\omega }-\{ 0\}$
,
$m\in {\omega }-\{ 0\}$
,
![]() $\{ N\in {\omega } -\{ 0\}\vert \ \sqrt {N}\in {\omega } ,\ m|\sqrt {N}\}\in {\mathcal {U}}$
, and similar properties can be added according to need.
$\{ N\in {\omega } -\{ 0\}\vert \ \sqrt {N}\in {\omega } ,\ m|\sqrt {N}\}\in {\mathcal {U}}$
, and similar properties can be added according to need.
Let
![]() $H^{u}$
be the (classical) ultraproduct
$H^{u}$
be the (classical) ultraproduct
![]() $\Pi _{N\in {\omega }}H_{N}/{\mathcal {U}}$
and
$\Pi _{N\in {\omega }}H_{N}/{\mathcal {U}}$
and
![]() $\mathbb {C}^{u}$
be the ultrapower
$\mathbb {C}^{u}$
be the ultrapower
![]() $\mathbb {C}^{{\omega }}/{\mathcal {U}}$
of the field of complex numbers
$\mathbb {C}^{{\omega }}/{\mathcal {U}}$
of the field of complex numbers
![]() $\mathbb {C}$
. Then
$\mathbb {C}$
. Then
![]() $H^{u}$
is a vector space over
$H^{u}$
is a vector space over
![]() $\mathbb {C}^{u}$
and by identifying elements of
$\mathbb {C}^{u}$
and by identifying elements of
![]() $\mathbb {C}$
with their images under the canonical embedding of
$\mathbb {C}$
with their images under the canonical embedding of
![]() $\mathbb {C}$
into
$\mathbb {C}$
into
![]() $\mathbb {C}^{u}$
, also a vector space over
$\mathbb {C}^{u}$
, also a vector space over
![]() $\mathbb {C}$
. There is also a pairing
$\mathbb {C}$
. There is also a pairing
![]() $\langle \cdot |\cdot \rangle ^{u}$
from
$\langle \cdot |\cdot \rangle ^{u}$
from
![]() $H^{u}$
to
$H^{u}$
to
![]() $\mathbb {C}^{u}$
which is obtained as the ultraproduct of the inner products
$\mathbb {C}^{u}$
which is obtained as the ultraproduct of the inner products
![]() $\langle \cdot |\cdot \rangle _{N}$
of
$\langle \cdot |\cdot \rangle _{N}$
of
![]() $H_{N}$
. And similarly we get a unary function
$H_{N}$
. And similarly we get a unary function
![]() $\Vert \cdot \Vert ^{u}_{2}$
. Notice that for all
$\Vert \cdot \Vert ^{u}_{2}$
. Notice that for all
![]() $v=(v_{N})_{N\in {\omega }}/{\mathcal {U}}\in H^{u}$
,
$v=(v_{N})_{N\in {\omega }}/{\mathcal {U}}\in H^{u}$
,
![]() $\Vert v\Vert ^{u}_{2}= (\sqrt {\langle v_{N}|v_{N}\rangle _{N}})_{N\in {\omega }}/{\mathcal {U}}$
and that
$\Vert v\Vert ^{u}_{2}= (\sqrt {\langle v_{N}|v_{N}\rangle _{N}})_{N\in {\omega }}/{\mathcal {U}}$
and that
![]() $((\sqrt {\langle v_{N}|v_{N}\rangle _{N}})_{N\in {\omega }}/{\mathcal {U}})^{2}=\langle v\vert v\rangle ^{u}$
. Similarly for all
$((\sqrt {\langle v_{N}|v_{N}\rangle _{N}})_{N\in {\omega }}/{\mathcal {U}})^{2}=\langle v\vert v\rangle ^{u}$
. Similarly for all
![]() $q=(q_{N})_{N\in {\omega }}/{\mathcal {U}}\in \mathbb {C}^{u}$
, we write
$q=(q_{N})_{N\in {\omega }}/{\mathcal {U}}\in \mathbb {C}^{u}$
, we write
![]() $\vert q\vert ^{u}$
for
$\vert q\vert ^{u}$
for
![]() $(\vert q_{N}\vert )_{N\in {\omega }}/{\mathcal {U}}$
. Notice that if we let X be the range of this ‘absolute value’, then
$(\vert q_{N}\vert )_{N\in {\omega }}/{\mathcal {U}}$
. Notice that if we let X be the range of this ‘absolute value’, then
![]() $\mathbb {R}^{u}=X\cup \{-r\vert \ r\in X\}$
is a real closed field containing the reals. In particular, it is linearly ordered and thus we can compare, e.g., the ‘norm’
$\mathbb {R}^{u}=X\cup \{-r\vert \ r\in X\}$
is a real closed field containing the reals. In particular, it is linearly ordered and thus we can compare, e.g., the ‘norm’
![]() $\Vert v\Vert ^{u}$
of
$\Vert v\Vert ^{u}$
of
![]() $v\in H^{u}$
and a rational number. Thus for all
$v\in H^{u}$
and a rational number. Thus for all
![]() $u,v\in H^{u}$
, if there is
$u,v\in H^{u}$
, if there is
![]() $q\in \mathbb {C}$
such that q is infinitely close to
$q\in \mathbb {C}$
such that q is infinitely close to
![]() $\langle u|v\rangle ^{u}$
, we write
$\langle u|v\rangle ^{u}$
, we write
![]() $\langle u\vert v\rangle $
for this q. If there is no such q, we write
$\langle u\vert v\rangle $
for this q. If there is no such q, we write
![]() $\langle u|v\rangle =\infty $
.
$\langle u|v\rangle =\infty $
.
Notation 2.2. When we define an element
![]() $(v_{N})_{N<{\omega }}/{\mathcal {U}}$
of
$(v_{N})_{N<{\omega }}/{\mathcal {U}}$
of
![]() $H^{u}$
, it is enough to define the vectors
$H^{u}$
, it is enough to define the vectors
![]() $v_{N}$
so that the definition makes sense for all N in some set that belongs to
$v_{N}$
so that the definition makes sense for all N in some set that belongs to
![]() ${\mathcal {U}}$
. This often simplifies notation considerably.
${\mathcal {U}}$
. This often simplifies notation considerably.
Now
![]() $H^{u}$
contains some structures of interest to us. Let us first look at
$H^{u}$
contains some structures of interest to us. Let us first look at
![]() $H^{\infty }$
: On
$H^{\infty }$
: On
![]() $H^{u}$
we define an equivalence relation
$H^{u}$
we define an equivalence relation
![]() $\sim $
so that
$\sim $
so that
![]() $u\sim v$
if
$u\sim v$
if
![]() $\Vert u-v\Vert ^{u}_{2}$
is infinitesimal (i.e., smaller than
$\Vert u-v\Vert ^{u}_{2}$
is infinitesimal (i.e., smaller than
![]() $1/n$
for all natural numbers n) and let
$1/n$
for all natural numbers n) and let
![]() $H^{\infty }=H^{u}/\sim $
. Now addition of elements of
$H^{\infty }=H^{u}/\sim $
. Now addition of elements of
![]() $H^{\infty }$
and for all
$H^{\infty }$
and for all
![]() $q\in \mathbb {C}$
, the multiplication by q are well-defined in
$q\in \mathbb {C}$
, the multiplication by q are well-defined in
![]() $H^{\infty }$
and thus
$H^{\infty }$
and thus
![]() $H^{\infty }$
is a vector space over
$H^{\infty }$
is a vector space over
![]() $\mathbb {C}$
. We define a partial pairing
$\mathbb {C}$
. We define a partial pairing
![]() $\langle \cdot |\cdot \rangle $
on
$\langle \cdot |\cdot \rangle $
on
![]() $H^{\infty }$
as follows: For all
$H^{\infty }$
as follows: For all
![]() $u,v\in H^{\infty }$
, if there is
$u,v\in H^{\infty }$
, if there is
![]() $q\in \mathbb {C}$
such that for all
$q\in \mathbb {C}$
such that for all
![]() $u'\in u/\sim $
and
$u'\in u/\sim $
and
![]() $v'\in v/\sim $
,
$v'\in v/\sim $
,
![]() $\langle u'|v'\rangle ^{u}=q$
, then we let
$\langle u'|v'\rangle ^{u}=q$
, then we let
![]() $\langle u|v\rangle =q$
and otherwise
$\langle u|v\rangle =q$
and otherwise
![]() $\langle u|v\rangle $
is
$\langle u|v\rangle $
is
![]() $\infty $
.
$\infty $
.
The second of these structures is the metric ultraproduct
![]() $H^{m}$
: We let
$H^{m}$
: We let
![]() $H^{m}$
be the set of all
$H^{m}$
be the set of all
![]() $v/\sim \in H^{\infty }$
such that
$v/\sim \in H^{\infty }$
such that
![]() $\Vert v\Vert ^{u}_{2}$
is finite (i.e., smaller than some natural number). Notice that
$\Vert v\Vert ^{u}_{2}$
is finite (i.e., smaller than some natural number). Notice that
![]() $H^{m}$
is still a vector space over
$H^{m}$
is still a vector space over
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $\langle \cdot |\cdot \rangle $
is total on
$\langle \cdot |\cdot \rangle $
is total on
![]() $H^{m}$
and, in fact, an inner product. This also gives a norm on
$H^{m}$
and, in fact, an inner product. This also gives a norm on
![]() $H^{m}$
but it is the same as
$H^{m}$
but it is the same as
![]() $\Vert \cdot \Vert _{2}$
defined above. Later, when considering spaces arising from other norms, we may write
$\Vert \cdot \Vert _{2}$
defined above. Later, when considering spaces arising from other norms, we may write
![]() $H^{m}_{2}$
for
$H^{m}_{2}$
for
![]() $H^{m}$
.
$H^{m}$
.
Remark 2.3. We could define
![]() $\sim $
also on
$\sim $
also on
![]() $\mathbb {C}^{u}$
by
$\mathbb {C}^{u}$
by
![]() $q\sim r$
if
$q\sim r$
if
![]() $\vert q-r\vert ^{u}$
is infinitesimal and let
$\vert q-r\vert ^{u}$
is infinitesimal and let
![]() $\mathbb {C}^{\infty }$
be
$\mathbb {C}^{\infty }$
be
![]() $\mathbb {C}^{u}/\sim $
. Notice that multiplication is not well defined in
$\mathbb {C}^{u}/\sim $
. Notice that multiplication is not well defined in
![]() $\mathbb {C}^{\infty }$
if one of the elements has infinite norm. Then we could let
$\mathbb {C}^{\infty }$
if one of the elements has infinite norm. Then we could let
![]() $\mathbb {C}^{m}$
be (the field of) all
$\mathbb {C}^{m}$
be (the field of) all
![]() $q/\sim \in \mathbb {C}^{\infty }$
such that
$q/\sim \in \mathbb {C}^{\infty }$
such that
![]() $\vert q\vert ^{u}$
is finite. Notice that
$\vert q\vert ^{u}$
is finite. Notice that
![]() $\mathbb {C}^{m}=\{ q/\sim \vert \ q\in \mathbb {C}\}$
and that for all
$\mathbb {C}^{m}=\{ q/\sim \vert \ q\in \mathbb {C}\}$
and that for all
![]() $u,v\in H^{m}$
, if
$u,v\in H^{m}$
, if
![]() $\langle u|v\rangle =q$
, then
$\langle u|v\rangle =q$
, then
![]() $q/\sim =\langle u|v\rangle ^{u}/\sim $
.
$q/\sim =\langle u|v\rangle ^{u}/\sim $
.
Let
![]() $A^{u}$
be the ultraproduct of the operators
$A^{u}$
be the ultraproduct of the operators
![]() $A_{N}$
. Since the operators
$A_{N}$
. Since the operators
![]() $A_{N}$
are uniformly bounded,
$A_{N}$
are uniformly bounded,
![]() $A^{u}$
induces a well-defined operator
$A^{u}$
induces a well-defined operator
![]() $A^{\infty }$
on
$A^{\infty }$
on
![]() $H^{\infty }$
and the restriction
$H^{\infty }$
and the restriction
![]() $A^{m}$
of
$A^{m}$
of
![]() $A^{\infty }$
to
$A^{\infty }$
to
![]() $H^{m}$
is a well-defined operator on
$H^{m}$
is a well-defined operator on
![]() $H^{m}$
. We can do the same for the
$H^{m}$
. We can do the same for the
![]() $A^{*}_{N}$
’s and get operators
$A^{*}_{N}$
’s and get operators
![]() $A^{*u}$
,
$A^{*u}$
,
![]() $A^{*\infty }$
and
$A^{*\infty }$
and
![]() $A^{*m}$
. Notice that
$A^{*m}$
. Notice that
![]() $(A^{m})^{*}=A^{*m}$
since being an adjoint is preserved in metric ultraproducts and that
$(A^{m})^{*}=A^{*m}$
since being an adjoint is preserved in metric ultraproducts and that
![]() $A^{m}$
and
$A^{m}$
and
![]() $A^{*m}$
commute since
$A^{*m}$
commute since
![]() $A_{N}$
and
$A_{N}$
and
![]() $A^{*}_{N}$
commute for all N and thus
$A^{*}_{N}$
commute for all N and thus
![]() $A^{m}$
is normal.
$A^{m}$
is normal.
Now the homomorphisms
![]() $F_N$
(from Definition 2.1) induce a homomorphism from the vector space
$F_N$
(from Definition 2.1) induce a homomorphism from the vector space
![]() $D(S)$
into
$D(S)$
into
![]() $H^m$
:
$H^m$
:
Definition 2.4. Let
![]() $F^m: D(S)\to H^m$
be given by
$F^m: D(S)\to H^m$
be given by
This is well-defined, as
![]() $\{F_N(f_P):N<{\omega }\}$
is bounded (see Definition 2.1). By
$\{F_N(f_P):N<{\omega }\}$
is bounded (see Definition 2.1). By
![]() $F^u$
we will denote the homomorphism from
$F^u$
we will denote the homomorphism from
![]() $D(S)$
to
$D(S)$
to
![]() $H^u$
:
$H^u$
:
Notice that
![]() $F^m(A_{D}(f_{P}))=A^{m}(F^m(f_{P}))$
and similarly for
$F^m(A_{D}(f_{P}))=A^{m}(F^m(f_{P}))$
and similarly for
![]() $A^{*}_{D}$
and
$A^{*}_{D}$
and
![]() $A^{*m}$
. We can also embed H into
$A^{*m}$
. We can also embed H into
![]() $H^m$
:
$H^m$
:
Definition 2.5. Let
![]() $G^m: H\to H^m$
be given by
$G^m: H\to H^m$
be given by
and denote
![]() $H^{Im}=rng(G^m)$
.
$H^{Im}=rng(G^m)$
.
Notice that
![]() $G^m$
is well-defined, as
$G^m$
is well-defined, as
for all N large enough. Notice also that for all
![]() $\psi \in H$
,
$\psi \in H$
,
![]() $G^{m}(A(\psi ))=A^{m}(G^{m}(\psi ))$
and the same for
$G^{m}(A(\psi ))=A^{m}(G^{m}(\psi ))$
and the same for
![]() $A^{*}$
and
$A^{*}$
and
![]() $A^{*m}$
. Also
$A^{*m}$
. Also
![]() $\Vert G^{m}(\psi )\Vert ^{m}_{2}=\Vert \psi \Vert _{2}$
and so
$\Vert G^{m}(\psi )\Vert ^{m}_{2}=\Vert \psi \Vert _{2}$
and so
![]() $G^{m}$
is an (isometric) embedding of the Hilbert space H into
$G^{m}$
is an (isometric) embedding of the Hilbert space H into
![]() $H^{m}$
and maps A to
$H^{m}$
and maps A to
![]() $A^{m}\restriction H^{Im}$
and
$A^{m}\restriction H^{Im}$
and
![]() $A^{*}$
to
$A^{*}$
to
![]() $A^{*m}\restriction H^{Im}$
.
$A^{*m}\restriction H^{Im}$
.
So we have seen the following:
Lemma 2.6.
![]() $G^{m}$
is an isometric isomorphism from H onto
$G^{m}$
is an isometric isomorphism from H onto
![]() $H^{Im}$
,
$H^{Im}$
,
![]() $G^{m}\circ A=A^{m}\circ G^{m}$
,
$G^{m}\circ A=A^{m}\circ G^{m}$
,
![]() $G^{m}\circ A^{*}=A^{*m}\circ G^{m}$
, and
$G^{m}\circ A^{*}=A^{*m}\circ G^{m}$
, and
![]() $A^{*m}$
and
$A^{*m}$
and
![]() $A^{*m}\restriction H^{Im}$
are the adjoints of
$A^{*m}\restriction H^{Im}$
are the adjoints of
![]() $A^{m}$
and
$A^{m}$
and
![]() $A^{m}\restriction H^{Im}$
, respectively.
$A^{m}\restriction H^{Im}$
, respectively.
Corollary 2.7. For all
![]() $f\in D(S)$
,
$f\in D(S)$
,
![]() $G^{m}(G(f))=F^m(f)$
.
$G^{m}(G(f))=F^m(f)$
.
Proof. Now
![]() $f=f_{P}$
for some
$f=f_{P}$
for some
![]() $P\in \mathbb {C} [X,Y]$
. Then
$P\in \mathbb {C} [X,Y]$
. Then
where the last identity follows from (4), (5), and (6) above.
As we are working with several spaces and functions, we have gathered the main ones in Figure 1 to act as a quick reference.

Figure 1 The main spaces and functions.
We now return to the reason for talking about A and
![]() $A^*$
instead of A and
$A^*$
instead of A and
![]() $A^{-1}$
, namely there are operators that are not obtained just by multiplying a unitary operator by a constant but that still allow for the sort of approximation we developed here.
$A^{-1}$
, namely there are operators that are not obtained just by multiplying a unitary operator by a constant but that still allow for the sort of approximation we developed here.
Example 2.8. Let
![]() $A=rU$
be an operator with a cyclic vector u on a Hilbert space
$A=rU$
be an operator with a cyclic vector u on a Hilbert space
![]() $H_1$
and
$H_1$
and
![]() $B=qV$
be an operator with a cyclic vector v on a Hilbert space
$B=qV$
be an operator with a cyclic vector v on a Hilbert space
![]() $H_2$
, where
$H_2$
, where
![]() $r,q\in \mathbb {C}$
,
$r,q\in \mathbb {C}$
,
![]() $r,q\neq 0$
,
$r,q\neq 0$
,
![]() $r\neq q$
, and U and V are unitary. Then consider the space
$r\neq q$
, and U and V are unitary. Then consider the space
![]() $H\subset H_1\oplus H_2$
spanned by the vectors
$H\subset H_1\oplus H_2$
spanned by the vectors
![]() $(A\oplus B)^i(A^*\oplus B^*)^j(u\oplus v)$
, for
$(A\oplus B)^i(A^*\oplus B^*)^j(u\oplus v)$
, for
![]() $i,j<{\omega }$
. This gives a space (H) and an operator
$i,j<{\omega }$
. This gives a space (H) and an operator
![]() $(A\oplus B)$
with a cyclic vector (
$(A\oplus B)$
with a cyclic vector (
![]() $u\oplus v$
) such that the operator is not a constant times a unitary operator, but one can still build spaces
$u\oplus v$
) such that the operator is not a constant times a unitary operator, but one can still build spaces
![]() $H_N$
as above (generated by vectors
$H_N$
as above (generated by vectors
![]() $(A\oplus B)^i(A^*\oplus B^*)^j(u\oplus v)$
with
$(A\oplus B)^i(A^*\oplus B^*)^j(u\oplus v)$
with
![]() $i,j\leq N$
).
$i,j\leq N$
).
Open question 2. What exactly is needed of the operator A for this kind of approximation technique to work?
In Section 4 we will use the method from this section applied to unitary operators, and use them to extend our approximating results to bounded self-adjoint operators. We leave it to future work to either find a way to extend the method of this section to all bounded normal operators or modify the construction for bounded self-adjoint operators from Section 4 to access bounded normal operators via a decomposition into self-adjoint operators.
3 Spectral measure
In this section we show how weighted counting measures in the finite dimensional spaces give rise to a measure on subsets of
![]() $\mathbb {C}$
. With this measure the vector space homomorphism
$\mathbb {C}$
. With this measure the vector space homomorphism
![]() $F^m$
from the previous section becomes an isometric embedding of
$F^m$
from the previous section becomes an isometric embedding of
![]() $L_2(S,\mu )$
into the metric ultraproduct.
$L_2(S,\mu )$
into the metric ultraproduct.
For all
![]() $N<{\omega }$
, we define a measure
$N<{\omega }$
, we define a measure
![]() $\mu _{N}$
for subsets X of
$\mu _{N}$
for subsets X of
![]() $\mathbb {C}$
: Recall that
$\mathbb {C}$
: Recall that
![]() $\phi =\sum _{k=0}^{D_{N}-1}\xi _{N}(k)u_{N}(k)$
and each
$\phi =\sum _{k=0}^{D_{N}-1}\xi _{N}(k)u_{N}(k)$
and each
![]() $\xi _{N}(k)$
is a non-negative real. We let
$\xi _{N}(k)$
is a non-negative real. We let
![]() $\mu _{N}(X)$
be the sum of all
$\mu _{N}(X)$
be the sum of all
![]() $\xi _{N}(k)^{2}$
such that
$\xi _{N}(k)^{2}$
such that
![]() $k<D_{N}$
and
$k<D_{N}$
and
![]() $\lambda _{N}(k)\in X$
. Note that, as
$\lambda _{N}(k)\in X$
. Note that, as
![]() $\lVert {\phi }\rVert =1$
,
$\lVert {\phi }\rVert =1$
,
![]() $\mu _N(X)\in [0,1]$
for all
$\mu _N(X)\in [0,1]$
for all
![]() $N<{\omega }$
and
$N<{\omega }$
and
![]() $X\subset \mathbb {C}$
. Then we define
$X\subset \mathbb {C}$
. Then we define
![]() $\mu ^{n}(X)$
to be the ultralimit
$\mu ^{n}(X)$
to be the ultralimit
![]() $\lim _{{\mathcal {U}}}\mu _{N}(X)$
of the measures
$\lim _{{\mathcal {U}}}\mu _{N}(X)$
of the measures
![]() $\mu _{N}(X)$
, i.e.,
$\mu _{N}(X)$
, i.e.,
![]() $\mu ^{n}(X)$
is the unique real r such that for all
$\mu ^{n}(X)$
is the unique real r such that for all
![]() $\varepsilon>0$
, the set
$\varepsilon>0$
, the set
We think of
![]() $\mu ^n$
as a sort of naive measure, as it is our main tool towards building a measure, but it is defined on all subsets of
$\mu ^n$
as a sort of naive measure, as it is our main tool towards building a measure, but it is defined on all subsets of
![]() $\mathbb {C}$
and we have no reason to believe it actually would be a measure. However, we can use it to build a Borel measure.
$\mathbb {C}$
and we have no reason to believe it actually would be a measure. However, we can use it to build a Borel measure.
Definition 3.1. For all reals
![]() $r\in [{-}M,M]$
we define lines
$r\in [{-}M,M]$
we define lines
![]() $I_{r}=\{\lambda \in S\vert \ Re(\lambda )=r\}$
and
$I_{r}=\{\lambda \in S\vert \ Re(\lambda )=r\}$
and
![]() $J_{r}=\{\lambda \in S\vert \ Im(\lambda )=r\}$
. For all
$J_{r}=\{\lambda \in S\vert \ Im(\lambda )=r\}$
. For all
![]() $\varepsilon>0$
we let
$\varepsilon>0$
we let
![]() $I_{r}^{\varepsilon }=\{\lambda \in S\vert \ \vert Re(\lambda )-r\vert <\varepsilon \}$
and
$I_{r}^{\varepsilon }=\{\lambda \in S\vert \ \vert Re(\lambda )-r\vert <\varepsilon \}$
and
![]() $J_{r}^{\varepsilon }=\{\lambda \in S\vert \ \vert Im(\lambda )-r\vert <\varepsilon \}$
. For a point
$J_{r}^{\varepsilon }=\{\lambda \in S\vert \ \vert Im(\lambda )-r\vert <\varepsilon \}$
. For a point
![]() $\lambda \in S$
and
$\lambda \in S$
and
![]() $\varepsilon>0$
, we let
$\varepsilon>0$
, we let
![]() $\lambda ^{\varepsilon }=\{ x\in S\vert \ \vert Re(\lambda )-Re(x)\vert ,\vert Im(\lambda )-Im(x)\vert <\varepsilon \}$
. We say that a real
$\lambda ^{\varepsilon }=\{ x\in S\vert \ \vert Re(\lambda )-Re(x)\vert ,\vert Im(\lambda )-Im(x)\vert <\varepsilon \}$
. We say that a real
![]() $r\in [{-}M,M]$
is nice if for all
$r\in [{-}M,M]$
is nice if for all
![]() $\delta>0$
there is
$\delta>0$
there is
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $\mu ^{n}(I^{\varepsilon }_{r}),\mu ^{n}(J^{\varepsilon }_{r})<\delta $
.
$\mu ^{n}(I^{\varepsilon }_{r}),\mu ^{n}(J^{\varepsilon }_{r})<\delta $
.
Lemma 3.2.
-
(i)
 $\mu ^{n}$
satisfies all the properties of a measure when restricted to finite collections of sets, e.g., if
$\mu ^{n}$
satisfies all the properties of a measure when restricted to finite collections of sets, e.g., if
 $X\subseteq Y$
, then
$X\subseteq Y$
, then
 $\mu ^{n}(X)\le \mu ^{n}(Y)$
and if
$\mu ^{n}(X)\le \mu ^{n}(Y)$
and if
 $X_{i}$
,
$X_{i}$
,
 $i<m$
, are disjoint, then
$i<m$
, are disjoint, then
 $\mu ^{n}(\cup _{i<m}X_{i})=\sum _{i<m}\mu ^{n}(X_{i})$
.
$\mu ^{n}(\cup _{i<m}X_{i})=\sum _{i<m}\mu ^{n}(X_{i})$
. -
(ii) The set of
 $r\in [{-}M,M]$
that are not nice is countable. Thus there is a countable dense subset
$r\in [{-}M,M]$
that are not nice is countable. Thus there is a countable dense subset
 $NI$
of
$NI$
of
 $[{-}M,M]$
such that every
$[{-}M,M]$
such that every
 $r\in NI$
is nice and
$r\in NI$
is nice and
 ${-}M,M\in NI$
.
${-}M,M\in NI$
.
Proof. (i): The claim is clear since each
![]() $\mu _{N}$
is a measure and thus has these properties.
$\mu _{N}$
is a measure and thus has these properties.
(ii): Suppose not. Since
![]() $-M$
and M are clearly nice, there must be uncountably many reals
$-M$
and M are clearly nice, there must be uncountably many reals
![]() $r\in [{-}M,M]$
that are not nice. Let these be
$r\in [{-}M,M]$
that are not nice. Let these be
![]() $r_{i}$
,
$r_{i}$
,
![]() $i<{\omega }_{1}$
. By symmetry and the pigeon hole principle we may assume that for all
$i<{\omega }_{1}$
. By symmetry and the pigeon hole principle we may assume that for all
![]() $i<{\omega }_{1}$
, the vertical lines witness this. Then by the pigeon hole principle again, we may assume that there is
$i<{\omega }_{1}$
, the vertical lines witness this. Then by the pigeon hole principle again, we may assume that there is
![]() $\delta>0$
such that for all
$\delta>0$
such that for all
![]() $i<{\omega }_{1}$
and
$i<{\omega }_{1}$
and
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $\mu ^{n}(I^{\varepsilon }_{r_{i}})>\delta $
. Let
$\mu ^{n}(I^{\varepsilon }_{r_{i}})>\delta $
. Let
![]() $K<{\omega }$
be such that
$K<{\omega }$
be such that
![]() $K\delta>1$
. Now for all
$K\delta>1$
. Now for all
![]() $i<K$
choose
$i<K$
choose
![]() $\varepsilon _{i}>0$
so that the sets
$\varepsilon _{i}>0$
so that the sets
![]() $I^{\varepsilon _{i}}_{r_{i}}$
,
$I^{\varepsilon _{i}}_{r_{i}}$
,
![]() $i<K$
, are disjoint. But now we can find
$i<K$
, are disjoint. But now we can find
![]() $N<{\omega }$
such that for all
$N<{\omega }$
such that for all
![]() $i<K$
,
$i<K$
,
![]() $\mu _{N}(I^{\varepsilon _{i}}_{r_{i}})>\delta $
. It follows that
$\mu _{N}(I^{\varepsilon _{i}}_{r_{i}})>\delta $
. It follows that
![]() $\mu _{N}(\cup _{i<K}I^{\varepsilon _{i}}_{r_{i}})>1$
, a contradiction.
$\mu _{N}(\cup _{i<K}I^{\varepsilon _{i}}_{r_{i}})>1$
, a contradiction.
Definition 3.3. Let
![]() $Sq^{*}$
be the set of all subsets Y such that there are
$Sq^{*}$
be the set of all subsets Y such that there are
![]() $r_{i}\in NI$
such that
$r_{i}\in NI$
such that
Now define
![]() $\mu ^{*}(Y)$
for any
$\mu ^{*}(Y)$
for any
![]() $Y\subseteq Int(S)$
(interior of S) to be the outer measure based on
$Y\subseteq Int(S)$
(interior of S) to be the outer measure based on
![]() $\mu ^{n}(X)$
,
$\mu ^{n}(X)$
,
![]() $X\in Sq^{*}$
, i.e.,
$X\in Sq^{*}$
, i.e.,
 $$ \begin{align*}\mu^{*}(Y)=\inf\{\sum_{i=0}^{\infty}\mu^{n}(X_{i})\vert\ X_{i}\in Sq^{*}, Y\subseteq\cup_{i<{\omega}}X_{i}\}.\end{align*} $$
$$ \begin{align*}\mu^{*}(Y)=\inf\{\sum_{i=0}^{\infty}\mu^{n}(X_{i})\vert\ X_{i}\in Sq^{*}, Y\subseteq\cup_{i<{\omega}}X_{i}\}.\end{align*} $$
As usual, we say that
![]() $X\subseteq Int(S)$
is measurable if for all
$X\subseteq Int(S)$
is measurable if for all
![]() $Y\subseteq Int(S)$
,
$Y\subseteq Int(S)$
,
![]() $\mu ^{*}(Y)=\mu ^{*}(Y\cap X)+\mu ^{*}(Y-X)$
. For
$\mu ^{*}(Y)=\mu ^{*}(Y\cap X)+\mu ^{*}(Y-X)$
. For
![]() $X\subseteq S$
(or
$X\subseteq S$
(or
![]() $X\subseteq \mathbb {C}$
), we let
$X\subseteq \mathbb {C}$
), we let
![]() $\mu ^{*}(X)=\mu ^{*}(X\cap Int(S))$
and X is measurable if
$\mu ^{*}(X)=\mu ^{*}(X\cap Int(S))$
and X is measurable if
![]() $X\cap Int(S)$
is. Since there is
$X\cap Int(S)$
is. Since there is
![]() $\varepsilon>0$
such that for all
$\varepsilon>0$
such that for all
![]() $N<{\omega }$
and
$N<{\omega }$
and
![]() $k<D_{N}$
,
$k<D_{N}$
,
![]() $\vert \lambda _{N}(k)\vert <M-\varepsilon $
, it is enough to look at subsets of
$\vert \lambda _{N}(k)\vert <M-\varepsilon $
, it is enough to look at subsets of
![]() $Int(S)$
(everything close to the boundary of S has naive measure zero). We write
$Int(S)$
(everything close to the boundary of S has naive measure zero). We write
![]() $\overline X$
for the closure of
$\overline X$
for the closure of
![]() $X\subseteq \mathbb {C}$
.
$X\subseteq \mathbb {C}$
.
Lemma 3.4. Let
![]() $Y\in Sq^{*}$
.
$Y\in Sq^{*}$
.
-
(i)
 $\mu ^{*}(Y)=\mu ^{*}(\overline Y)=\mu ^{n}(Y)=\mu ^{n}(\overline Y)$
.
$\mu ^{*}(Y)=\mu ^{*}(\overline Y)=\mu ^{n}(Y)=\mu ^{n}(\overline Y)$
. -
(ii) Y is measurable.
Proof. (i): Clearly
![]() $\mu ^{*}(Y)\le \mu ^{*}(\overline Y)$
. From the choice of
$\mu ^{*}(Y)\le \mu ^{*}(\overline Y)$
. From the choice of
![]() $Sq^{*}$
it follows easily that for all
$Sq^{*}$
it follows easily that for all
![]() $\varepsilon>0$
, there is
$\varepsilon>0$
, there is
![]() $X\in Sq^{*}$
such that
$X\in Sq^{*}$
such that
![]() $\vert \mu ^{n}(X)-\mu ^{n}(Y)\vert <\varepsilon $
and
$\vert \mu ^{n}(X)-\mu ^{n}(Y)\vert <\varepsilon $
and
![]() $\overline Y\subseteq X$
. Thus
$\overline Y\subseteq X$
. Thus
![]() $\mu ^{*}(\overline Y)\le \mu ^{n}(Y)$
and
$\mu ^{*}(\overline Y)\le \mu ^{n}(Y)$
and
![]() $\mu ^{n}(\overline Y)=\mu ^{n}(Y)$
. Now for a contradiction, suppose that
$\mu ^{n}(\overline Y)=\mu ^{n}(Y)$
. Now for a contradiction, suppose that
![]() $\mu ^{*}(Y) +\varepsilon <\mu ^{n}(Y)$
for some
$\mu ^{*}(Y) +\varepsilon <\mu ^{n}(Y)$
for some
![]() $\varepsilon>0$
. Then we can find
$\varepsilon>0$
. Then we can find
![]() $Y_{i}\in Sq^*$
,
$Y_{i}\in Sq^*$
,
![]() $i<{\omega }$
, such that
$i<{\omega }$
, such that
![]() $Y\subseteq \cup _{i<{\omega }}Y_{i}$
and
$Y\subseteq \cup _{i<{\omega }}Y_{i}$
and
![]() $\sum _{i<{\omega }}\mu ^{n}(Y_{i}) +\varepsilon <\mu ^{n}(Y)$
. But then we can find
$\sum _{i<{\omega }}\mu ^{n}(Y_{i}) +\varepsilon <\mu ^{n}(Y)$
. But then we can find
![]() $X\in Sq^{*}$
such that
$X\in Sq^{*}$
such that
![]() $\overline X\subseteq Y$
and
$\overline X\subseteq Y$
and
![]() $\mu ^{n}(Y-\overline X)<\varepsilon $
. Since
$\mu ^{n}(Y-\overline X)<\varepsilon $
. Since
![]() $\overline X$
is compact, there is
$\overline X$
is compact, there is
![]() $K<{\omega }$
such that
$K<{\omega }$
such that
![]() $\overline X\subseteq \cup _{i<K}Y_{i}$
. Now
$\overline X\subseteq \cup _{i<K}Y_{i}$
. Now
a contradiction by Lemma 3.2.
(ii): By the definition of the outer measure
![]() $\mu ^*$
, and by considering coverings, it is enough to show that if
$\mu ^*$
, and by considering coverings, it is enough to show that if
![]() $X\in Sq^{*}$
, then
$X\in Sq^{*}$
, then
![]() $\mu ^{*}(X-Y)+\mu ^{*}(X\cap Y)=\mu ^{*}(X)$
. Clearly
$\mu ^{*}(X-Y)+\mu ^{*}(X\cap Y)=\mu ^{*}(X)$
. Clearly
![]() $\mu ^{*}(X-Y)+\mu ^{*}(X\cap Y)\ge \mu ^{*}(X)$
. On the other hand there are
$\mu ^{*}(X-Y)+\mu ^{*}(X\cap Y)\ge \mu ^{*}(X)$
. On the other hand there are
![]() $k\le 4$
and disjoint
$k\le 4$
and disjoint
![]() $Z_{i}\in Sq^{*}$
,
$Z_{i}\in Sq^{*}$
,
![]() $i<k$
, such that
$i<k$
, such that
![]() $\cup _{i<k}Z_{i}\subseteq X-Y$
and
$\cup _{i<k}Z_{i}\subseteq X-Y$
and
![]() $X-Y\subseteq \cup _{i<k}\overline Z_{i}$
. Notice that
$X-Y\subseteq \cup _{i<k}\overline Z_{i}$
. Notice that
![]() $X\cap Y\in Sq^{*}$
. Now
$X\cap Y\in Sq^{*}$
. Now
 $$ \begin{gather*}\mu^{*}(X-Y)\le\mu^{*}(\cup_{i<k}\overline Z_{i})\le\sum_{i<k}\mu^{*}(\overline Z_{i})=\\[5pt]=\sum_{i<k}\mu^{*}(Z_{i})=\sum_{i<k}\mu^{n}(Z_{i})=(\sum_{i<k}\mu^{n}(Z_{i}))+\mu^{n}(X\cap Y)-\mu^{n}(X\cap Y)\le\\[5pt]\le\mu^{n}((X\cap Y)\cup\cup_{i<k}Z_{i})-\mu^{n}(X\cap Y)\le\mu^{n}(X)-\mu^{n}(X\cap Y)=\mu^{*}(X)-\mu^{*}(X\cap Y).\end{gather*} $$
$$ \begin{gather*}\mu^{*}(X-Y)\le\mu^{*}(\cup_{i<k}\overline Z_{i})\le\sum_{i<k}\mu^{*}(\overline Z_{i})=\\[5pt]=\sum_{i<k}\mu^{*}(Z_{i})=\sum_{i<k}\mu^{n}(Z_{i})=(\sum_{i<k}\mu^{n}(Z_{i}))+\mu^{n}(X\cap Y)-\mu^{n}(X\cap Y)\le\\[5pt]\le\mu^{n}((X\cap Y)\cup\cup_{i<k}Z_{i})-\mu^{n}(X\cap Y)\le\mu^{n}(X)-\mu^{n}(X\cap Y)=\mu^{*}(X)-\mu^{*}(X\cap Y).\end{gather*} $$
Now as usual one can see that the collection of measurable sets is closed under countable unions and complements. In particular every Borel set (
![]() $\subseteq S$
) is measurable. For measurable X (
$\subseteq S$
) is measurable. For measurable X (
![]() $\subseteq S$
), we write
$\subseteq S$
), we write
![]() $\mu (X)=\mu ^{*}(X)$
and then
$\mu (X)=\mu ^{*}(X)$
and then
![]() $\mu $
is a Borel measure on S. Notice that by Lemma 3.4,
$\mu $
is a Borel measure on S. Notice that by Lemma 3.4,
![]() $\mu (S)=\mu ^{*}(S)=\mu ^{n}(S)=1$
(recall Equation (7) and that
$\mu (S)=\mu ^{*}(S)=\mu ^{n}(S)=1$
(recall Equation (7) and that
![]() $\phi $
has norm
$\phi $
has norm
![]() $1$
).
$1$
).
When working with the measure and later for constructing rigged Hilbert spaces, it will be convenient to have a sequence of refinements in
![]() $Sq^*$
.
$Sq^*$
.
Definition 3.5. Let, for each
![]() $k<\omega $
,
$k<\omega $
,
![]() $Sq_{k}\subseteq Sq^{*}$
be a finite set so that:
$Sq_{k}\subseteq Sq^{*}$
be a finite set so that:
-
(a) the elements of
 $Sq_{k}$
are disjoint,
$Sq_{k}$
are disjoint, -
(b)
 $\cup _{X\in Sq_{k}}\overline X =S$
,
$\cup _{X\in Sq_{k}}\overline X =S$
, -
(c) for all
 $X\in Sq^{*}$
and
$X\in Sq^{*}$
and
 $m<{\omega }$
, there are
$m<{\omega }$
, there are
 $m<k<{\omega }$
and
$m<k<{\omega }$
and
 $Z\subseteq Sq_{k}$
such that
$Z\subseteq Sq_{k}$
such that
 $\overline X=\cup _{Y\in Z}\overline Y$
,
$\overline X=\cup _{Y\in Z}\overline Y$
, -
(d) if
 $k<l<{\omega }$
,
$k<l<{\omega }$
,
 $X\in Sq_{k}$
, then there is
$X\in Sq_{k}$
, then there is
 $Z\subseteq Sq_{l}$
such that
$Z\subseteq Sq_{l}$
such that
 $\overline X =\cup _{Y\in Z}\overline Y$
, and
$\overline X =\cup _{Y\in Z}\overline Y$
, and -
(e) if
 $Y=\{ \lambda \in S\vert \ r_{0}<Re(\lambda )<r_{1},\ r_{2}<Im(\lambda )<r_{3}\}\in Sq_{k}$
, then
$Y=\{ \lambda \in S\vert \ r_{0}<Re(\lambda )<r_{1},\ r_{2}<Im(\lambda )<r_{3}\}\in Sq_{k}$
, then
 $r_{0}<r_{1}$
,
$r_{0}<r_{1}$
,
 $r_{1}-r_{0}<2M/(k+1)$
,
$r_{1}-r_{0}<2M/(k+1)$
,
 $r_{2}<r_{3}$
and
$r_{2}<r_{3}$
and
 $r_{3}-r_{2}<2M/(k+1)$
.
$r_{3}-r_{2}<2M/(k+1)$
.
We let
![]() $Sq=\cup _{k<{\omega }}Sq_{k}$
.
$Sq=\cup _{k<{\omega }}Sq_{k}$
.
Remark 3.6. Now by Lemma 3.4, it is easy to see that for all
![]() $X\subseteq S$
,
$X\subseteq S$
,
 $$ \begin{align*}\mu^{*}(X)=\inf\{\sum_{i=0}^{\infty}\mu^{n}(X_{i})\vert\ X_{i}\in Sq, X\subseteq\cup_{i<{\omega}}\overline X_{i}\} .\end{align*} $$
$$ \begin{align*}\mu^{*}(X)=\inf\{\sum_{i=0}^{\infty}\mu^{n}(X_{i})\vert\ X_{i}\in Sq, X\subseteq\cup_{i<{\omega}}\overline X_{i}\} .\end{align*} $$
We will use this frequently without mentioning it.
Now
![]() $L_{2}(S,\mu )$
is a Hilbert space and we write
$L_{2}(S,\mu )$
is a Hilbert space and we write
![]() $\Vert \cdot \Vert _{2}$
also for the norm of this space. Elements of
$\Vert \cdot \Vert _{2}$
also for the norm of this space. Elements of
![]() $L_{2}(S,\mu )$
are equivalence classes of the equivalence relation
$L_{2}(S,\mu )$
are equivalence classes of the equivalence relation
![]() $\Vert f-g\Vert _{2}=0$
and we write
$\Vert f-g\Vert _{2}=0$
and we write
![]() $[f]_{2}$
for these equivalence classes. Then as usual we write
$[f]_{2}$
for these equivalence classes. Then as usual we write
![]() $C(S)$
also for
$C(S)$
also for
![]() $\{ [f]_{2}\vert \ f\in C(S)\}$
and similarly for
$\{ [f]_{2}\vert \ f\in C(S)\}$
and similarly for
![]() $D(S)$
. For each equivalence class
$D(S)$
. For each equivalence class
![]() $x\in C(S)$
we fix a continuous
$x\in C(S)$
we fix a continuous
![]() $f_{x}:S\rightarrow \mathbb {C}$
so that
$f_{x}:S\rightarrow \mathbb {C}$
so that
![]() $x=[f_{x}]_{2}$
. We will see later (in Lemma 3.12) that this determines
$x=[f_{x}]_{2}$
. We will see later (in Lemma 3.12) that this determines
![]() $f_{x}$
on
$f_{x}$
on
![]() $\sigma (A)$
and what
$\sigma (A)$
and what
![]() $f_x$
does outside
$f_x$
does outside
![]() $\sigma (A)$
doesn’t matter. Now later when a function gives a value in
$\sigma (A)$
doesn’t matter. Now later when a function gives a value in
![]() $C(S)$
which is an equivalence class, we can think of it also as a continuous function from S to
$C(S)$
which is an equivalence class, we can think of it also as a continuous function from S to
![]() $\mathbb {C}$
. Thus
$\mathbb {C}$
. Thus
![]() $L_{2}(S,\mu )$
and
$L_{2}(S,\mu )$
and
![]() $L_{2}(\sigma (A),\mu \restriction \sigma (A))$
are naturally isomorphic since every
$L_{2}(\sigma (A),\mu \restriction \sigma (A))$
are naturally isomorphic since every
![]() $f\in C(\sigma (A))$
extends to a (bounded uniformly) continuous function
$f\in C(\sigma (A))$
extends to a (bounded uniformly) continuous function
![]() $f'\in C(S)$
.
$f'\in C(S)$
.
Our next step is to show that the mappings
![]() $F^m:D(S)\to H^m$
and
$F^m:D(S)\to H^m$
and
![]() $G:D(S)\to H$
are not only vector space homomorphisms, but also isometries under the
$G:D(S)\to H$
are not only vector space homomorphisms, but also isometries under the
![]() $L_2$
norm, which will let us define
$L_2$
norm, which will let us define
![]() $F^m([f]_{2})=F^m(f)$
and
$F^m([f]_{2})=F^m(f)$
and
![]() $G([f]_{2})=G(f)$
to get isometric embeddings of
$G([f]_{2})=G(f)$
to get isometric embeddings of
![]() $L_2(S,\mu )$
into
$L_2(S,\mu )$
into
![]() $H^m$
and H respectively.
$H^m$
and H respectively.
Lemma 3.7. For all
![]() $P\in \mathbb {C} [X,Y]$
,
$P\in \mathbb {C} [X,Y]$
,
![]() $\Vert F^u(f_{P})\Vert _{2}=\Vert f_{P}\Vert _{2}$
.
$\Vert F^u(f_{P})\Vert _{2}=\Vert f_{P}\Vert _{2}$
.
Proof. This proof is essentially the same as the proof that shows that continuous functions are Riemann integrable. Let
![]() $1>\varepsilon >0$
,
$1>\varepsilon >0$
,
![]() $m=1+ \sup \{\vert f_{P}(\lambda )\vert \ \vert \ \lambda \in S\}$
and choose
$m=1+ \sup \{\vert f_{P}(\lambda )\vert \ \vert \ \lambda \in S\}$
and choose
![]() $k>0$
so that if
$k>0$
so that if
![]() $\vert \lambda -\lambda '\vert <4M/k$
(which happens for all
$\vert \lambda -\lambda '\vert <4M/k$
(which happens for all
![]() $\lambda ,\lambda '\in \overline Y$
, for
$\lambda ,\lambda '\in \overline Y$
, for
![]() $Y\in Sq_k$
), then
$Y\in Sq_k$
), then
![]() $\vert f_{P}(\lambda )-f_{P}(\lambda ')\vert <\varepsilon /8m$
. Then we can choose
$\vert f_{P}(\lambda )-f_{P}(\lambda ')\vert <\varepsilon /8m$
. Then we can choose
![]() $W\in {\mathcal {U}}$
such that for all
$W\in {\mathcal {U}}$
such that for all
![]() $N\in W$
and
$N\in W$
and
![]() $Y\in Sq_{k}$
, both
$Y\in Sq_{k}$
, both
![]() $\vert \mu (Y)-\mu _{N}(Y)\vert $
and
$\vert \mu (Y)-\mu _{N}(Y)\vert $
and
![]() $\vert \mu (\overline Y)-\mu _{N}(\overline Y)\vert $
are
$\vert \mu (\overline Y)-\mu _{N}(\overline Y)\vert $
are
![]() $ {<\varepsilon /(4m^{2}\vert Sq_{k}\vert )}$
. Notice that if we let X be the union of all
$ {<\varepsilon /(4m^{2}\vert Sq_{k}\vert )}$
. Notice that if we let X be the union of all
![]() $\overline Y-Y$
,
$\overline Y-Y$
,
![]() $Y\in Sq_{k}$
, then
$Y\in Sq_{k}$
, then
![]() $\mu (X)=0$
, and
$\mu (X)=0$
, and
 $$ \begin{align*}\lVert{\sum_{\lambda_{N}(k)\in X}\xi_{N}(k)f_{P}(\lambda_{N}(k))u_{N}(k)}\rVert_2^2\leq\mu_N(X)m^2<\varepsilon/4.\end{align*} $$
$$ \begin{align*}\lVert{\sum_{\lambda_{N}(k)\in X}\xi_{N}(k)f_{P}(\lambda_{N}(k))u_{N}(k)}\rVert_2^2\leq\mu_N(X)m^2<\varepsilon/4.\end{align*} $$
Then
 $$ \begin{align*} \vert\ (\Vert F_{N}(f_{P})\Vert_{2})^{2}-(\Vert f_{P}\Vert_{2})^{2}\ \vert =\vert\ \sum_{k<D_N}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 - \int_S\lvert{f_P(x)}\rvert^2d\mu \ \vert\\ =\vert\ \sum_{\lambda_N(k)\in X}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 +\sum_{Y\in Sq_k}\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2\\ - \sum_{Y\in Sq_k}\int_Y\lvert{f_P(x)}\rvert^2d\mu \ \vert\qquad\ \quad\qquad\\ \leq \varepsilon/4 +\sum_{Y\in Sq_k}\lvert{\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 - \int_Y\lvert{f_P(x)}\rvert^2d\mu}\rvert, \end{align*} $$
$$ \begin{align*} \vert\ (\Vert F_{N}(f_{P})\Vert_{2})^{2}-(\Vert f_{P}\Vert_{2})^{2}\ \vert =\vert\ \sum_{k<D_N}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 - \int_S\lvert{f_P(x)}\rvert^2d\mu \ \vert\\ =\vert\ \sum_{\lambda_N(k)\in X}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 +\sum_{Y\in Sq_k}\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2\\ - \sum_{Y\in Sq_k}\int_Y\lvert{f_P(x)}\rvert^2d\mu \ \vert\qquad\ \quad\qquad\\ \leq \varepsilon/4 +\sum_{Y\in Sq_k}\lvert{\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 - \int_Y\lvert{f_P(x)}\rvert^2d\mu}\rvert, \end{align*} $$
and for each
![]() $Y\in Sq_k$
$Y\in Sq_k$
 $$ \begin{align*} \lvert{\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 - \int_Y\lvert{f_P(x)}\rvert^2d\mu}\rvert\qquad\qquad\qquad\\ \leq \int_Y \left(\frac{\sum_{l_N(k)\in Y}\xi_N(k)^2\lvert{\lvert{f_P(\lambda_N(k))}\rvert^2-\lvert{f_P(x)}\rvert^2}\rvert}{\mu(Y)}\right.\\ \left.\quad +\lvert{\frac{\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(x)}\rvert^2}{\mu(Y)}-\lvert{f_P(x)}\rvert^2}\rvert\right)d\mu\\ \leq \int_Y \left(\frac{\mu_N(Y)2m\frac{\varepsilon}{8m}}{\mu(Y)}+\lvert{\frac{\mu_N(Y)}{\mu(Y)}-1}\rvert m^2\right)d\mu\\ =\mu_N(Y)\frac{\varepsilon}{4}+\lvert{\mu_N(Y)-\mu(Y)}\rvert m^2\\ < \mu_N(Y)\frac{\varepsilon}{4}+\frac{\varepsilon}{4\lvert{Sq_k}\rvert}. \end{align*} $$
$$ \begin{align*} \lvert{\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 - \int_Y\lvert{f_P(x)}\rvert^2d\mu}\rvert\qquad\qquad\qquad\\ \leq \int_Y \left(\frac{\sum_{l_N(k)\in Y}\xi_N(k)^2\lvert{\lvert{f_P(\lambda_N(k))}\rvert^2-\lvert{f_P(x)}\rvert^2}\rvert}{\mu(Y)}\right.\\ \left.\quad +\lvert{\frac{\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(x)}\rvert^2}{\mu(Y)}-\lvert{f_P(x)}\rvert^2}\rvert\right)d\mu\\ \leq \int_Y \left(\frac{\mu_N(Y)2m\frac{\varepsilon}{8m}}{\mu(Y)}+\lvert{\frac{\mu_N(Y)}{\mu(Y)}-1}\rvert m^2\right)d\mu\\ =\mu_N(Y)\frac{\varepsilon}{4}+\lvert{\mu_N(Y)-\mu(Y)}\rvert m^2\\ < \mu_N(Y)\frac{\varepsilon}{4}+\frac{\varepsilon}{4\lvert{Sq_k}\rvert}. \end{align*} $$
Putting this together (and recalling
![]() $\mu _N(S)=1$
), we get
$\mu _N(S)=1$
), we get
from which the claim follows.
Corollary 3.8.
![]() $F^m([f]_{2})=F^m(f)$
and
$F^m([f]_{2})=F^m(f)$
and
![]() $G([f]_{2})=G(f)$
are isometric embeddings of
$G([f]_{2})=G(f)$
are isometric embeddings of
![]() $L_2(S,\mu )$
into
$L_2(S,\mu )$
into
![]() $H^m$
and H respectively.
$H^m$
and H respectively.
Proof. By the lemma above, and noting that
![]() $G=(G^{m})^{-1}F^m$
(see Corollary 2.7), we see that
$G=(G^{m})^{-1}F^m$
(see Corollary 2.7), we see that
![]() $F^m$
and G are well-defined on the
$F^m$
and G are well-defined on the
![]() $\lVert {\cdot }\rVert _2$
equivalence classes of
$\lVert {\cdot }\rVert _2$
equivalence classes of
![]() $D(S)$
. Now we notice that
$D(S)$
. Now we notice that
![]() $\mathbb {C} [X,Y]$
is closed under the function
$\mathbb {C} [X,Y]$
is closed under the function
![]() $f\mapsto f^{*}$
, where
$f\mapsto f^{*}$
, where
![]() $f^{*}(\lambda )=\overline {f(\lambda )}$
. And thus by Stone–Weierstrass,
$f^{*}(\lambda )=\overline {f(\lambda )}$
. And thus by Stone–Weierstrass,
![]() $D(S)$
is dense in
$D(S)$
is dense in
![]() $C(S)$
even in the uniform convergence topology (we will need this later). And since
$C(S)$
even in the uniform convergence topology (we will need this later). And since
![]() $C(S)$
is dense in
$C(S)$
is dense in
![]() $L_{2}(S,\mu )$
, see, e.g., [Reference Bogachev2, Corollary 4.2.2],
$L_{2}(S,\mu )$
, see, e.g., [Reference Bogachev2, Corollary 4.2.2],
![]() $D(S)$
is dense in
$D(S)$
is dense in
![]() $L_{2}(S,\mu )$
. Thus we can extend the functions
$L_{2}(S,\mu )$
. Thus we can extend the functions
![]() $F^m$
and G to all of
$F^m$
and G to all of
![]() $L_{2}(S,\mu )$
by continuity.
$L_{2}(S,\mu )$
by continuity.
Remark 3.9. Recall that on
![]() $D(S)$
, we have
$D(S)$
, we have
![]() $A_D(f_P)(\lambda )=\lambda f_P(\lambda )$
and
$A_D(f_P)(\lambda )=\lambda f_P(\lambda )$
and
![]() $A^*_D(f_P)(\lambda )=\overline \lambda f_P(\lambda )$
. These can also be defined on the
$A^*_D(f_P)(\lambda )=\overline \lambda f_P(\lambda )$
. These can also be defined on the
![]() $\lVert {\cdot }\rVert _2$
equivalence classes by
$\lVert {\cdot }\rVert _2$
equivalence classes by
![]() $A_{D}([f]_{2})=[A_{D}(f)]_{2}$
(and similarly for
$A_{D}([f]_{2})=[A_{D}(f)]_{2}$
(and similarly for
![]() $A^{*}_{D}$
), and then extend it to all of
$A^{*}_{D}$
), and then extend it to all of
![]() $L_2(S,\mu )$
by continuity.
$L_2(S,\mu )$
by continuity.
Corollary 3.10.
![]() $F^m$
is an isometric isomorphism from
$F^m$
is an isometric isomorphism from
![]() $L_{2}(S,\mu )$
to
$L_{2}(S,\mu )$
to
![]() $H^{Im}$
and
$H^{Im}$
and
![]() ${A^{m}\restriction H^{Im}=F^mA_{D}(F^m)^{-1}}$
. Thus also
${A^{m}\restriction H^{Im}=F^mA_{D}(F^m)^{-1}}$
. Thus also
![]() $G=(G^{m})^{-1}F^m$
is an isometric isomorphism from
$G=(G^{m})^{-1}F^m$
is an isometric isomorphism from
![]() $L_{2}(S,\mu )$
to H and
$L_{2}(S,\mu )$
to H and
![]() $A=GA_{D}G^{-1}$
.
$A=GA_{D}G^{-1}$
.
We have been looking at
![]() $L_2(S,\mu )$
, where S was chosen to be a ‘big enough’ set. However,
$L_2(S,\mu )$
, where S was chosen to be a ‘big enough’ set. However,
![]() $\mu $
only puts weight on part of this set, and next we will show that set is exactly the spectrum of A. As pointed out above, there is a rational number
$\mu $
only puts weight on part of this set, and next we will show that set is exactly the spectrum of A. As pointed out above, there is a rational number
![]() ${0<q<M}$
such that for all
${0<q<M}$
such that for all
![]() $N<{\omega }$
, the norm of
$N<{\omega }$
, the norm of
![]() $A_{N}$
is
$A_{N}$
is
![]() $<q$
since the norm of
$<q$
since the norm of
![]() $A_{N}$
is at most the norm of A. Thus if we let
$A_{N}$
is at most the norm of A. Thus if we let
![]() $S^{-}=\{\lambda \in \mathbb {C}\vert \ -M< Re(\lambda )<M, -M< Im(\lambda )<M\}$
then
$S^{-}=\{\lambda \in \mathbb {C}\vert \ -M< Re(\lambda )<M, -M< Im(\lambda )<M\}$
then
![]() $\mu (S^{-})=\mu (S)=1$
.
$\mu (S^{-})=\mu (S)=1$
.
Definition 3.11. Let
![]() $\sigma (A)$
be the set of all
$\sigma (A)$
be the set of all
![]() $\lambda \in \mathbb {C}$
such that
$\lambda \in \mathbb {C}$
such that
![]() $A-\lambda I$
does not have a bounded inverse. Notice that
$A-\lambda I$
does not have a bounded inverse. Notice that
![]() $\lambda \in \sigma (A)$
iff for all
$\lambda \in \sigma (A)$
iff for all
![]() $\varepsilon>0$
, there is
$\varepsilon>0$
, there is
![]() $\psi \in H$
such that
$\psi \in H$
such that
![]() $\Vert \psi \Vert _{2}=1$
and
$\Vert \psi \Vert _{2}=1$
and
![]() $\Vert A(\psi )-\lambda \psi \Vert _{2}<\varepsilon $
. We let
$\Vert A(\psi )-\lambda \psi \Vert _{2}<\varepsilon $
. We let
![]() $\tilde {\sigma }(A)$
be the set of all
$\tilde {\sigma }(A)$
be the set of all
![]() $\lambda \in S^{-}$
such that every open neighborhood of
$\lambda \in S^{-}$
such that every open neighborhood of
![]() $\lambda $
that is contained in
$\lambda $
that is contained in
![]() $S^{-}$
has measure
$S^{-}$
has measure
![]() $>0$
.
$>0$
.
Lemma 3.12.
![]() $\sigma (A)=\tilde {\sigma }(A)$
.
$\sigma (A)=\tilde {\sigma }(A)$
.
Proof. By Corollary 3.10, it is enough to show that
![]() $\sigma (A_{D})=\tilde {\sigma }(A)$
, where
$\sigma (A_{D})=\tilde {\sigma }(A)$
, where
![]() $\sigma (A_{D})$
is defined as
$\sigma (A_{D})$
is defined as
![]() $\sigma (A)$
was. Also if
$\sigma (A)$
was. Also if
![]() $\lambda \not \in S^{-}$
,
$\lambda \not \in S^{-}$
,
![]() $\lambda $
does not belong to either of the sets. So suppose that
$\lambda $
does not belong to either of the sets. So suppose that
![]() $\lambda \in S^{-}$
.
$\lambda \in S^{-}$
.
We write
![]() $B_{r}(\lambda )$
, r a positive real number, for the set of all
$B_{r}(\lambda )$
, r a positive real number, for the set of all
![]() $\lambda '\in \mathbb {C}$
such that
$\lambda '\in \mathbb {C}$
such that
![]() $\vert \lambda -\lambda '\vert <r$
. Now if for some r,
$\vert \lambda -\lambda '\vert <r$
. Now if for some r,
![]() $B_{r}(\lambda )\subseteq S^{-}$
and
$B_{r}(\lambda )\subseteq S^{-}$
and
![]() $\mu (B_{r}(\lambda ))=0$
, then it is easy to see that
$\mu (B_{r}(\lambda ))=0$
, then it is easy to see that
![]() $\Vert A_{D}(f)-\lambda f\Vert _{2}\ge r$
for all f with norm
$\Vert A_{D}(f)-\lambda f\Vert _{2}\ge r$
for all f with norm
![]() $1$
and thus
$1$
and thus
![]() $\lambda \not \in \sigma (A_{D})$
. On the other hand, if for all positive r such that
$\lambda \not \in \sigma (A_{D})$
. On the other hand, if for all positive r such that
![]() $B_{r}(\lambda )\subseteq S^{-}$
,
$B_{r}(\lambda )\subseteq S^{-}$
,
![]() $\mu (B_{r}(\lambda ))>0$
, then for all such r, we can find
$\mu (B_{r}(\lambda ))>0$
, then for all such r, we can find
![]() $f\in C(S )$
such that
$f\in C(S )$
such that
![]() $\Vert f\Vert _{2}=1$
and
$\Vert f\Vert _{2}=1$
and
![]() $f(x)=0$
for all
$f(x)=0$
for all
![]() $x\in S-B_{r}(\lambda )$
. Then
$x\in S-B_{r}(\lambda )$
. Then
![]() $\Vert A_{D}(f)-\lambda f\Vert _{2}<r$
. Thus
$\Vert A_{D}(f)-\lambda f\Vert _{2}<r$
. Thus
![]() $\lambda \in \sigma (A_{D})$
.
$\lambda \in \sigma (A_{D})$
.
Corollary 3.13.
![]() $\mu (\sigma (A))=1$
and
$\mu (\sigma (A))=1$
and
![]() $\mu (S-\sigma (A))=0$
.
$\mu (S-\sigma (A))=0$
.
Proof.
![]() $\sigma (A)=\tilde {\sigma }(A)$
is a closed set and thus measurable and thus the claims follow from Lemma 3.12 and
$\sigma (A)=\tilde {\sigma }(A)$
is a closed set and thus measurable and thus the claims follow from Lemma 3.12 and
![]() $\mu (S)=\mu (S^-)=1$
.
$\mu (S)=\mu (S^-)=1$
.
Looking back at the constructions of this and the past section, one notes that the finite dimensional spaces
![]() $H_N$
depend on the choice of
$H_N$
depend on the choice of
![]() $\phi $
, and thus it is likely that one gets different
$\phi $
, and thus it is likely that one gets different
![]() $H^u$
and
$H^u$
and
![]() $H^m$
depending on the choice of cyclic vector. We have not looked into this, as the whole of these spaces are too big for our interest. As every
$H^m$
depending on the choice of cyclic vector. We have not looked into this, as the whole of these spaces are too big for our interest. As every
![]() $H_N$
has a part, where the operator is replaced by a wraparound-mapping, these erroneous parts will show up in the ultraproduct, and we are really interested only in parts stemming from the original operator. There are subspaces where these errors disappear, and one of them is
$H_N$
has a part, where the operator is replaced by a wraparound-mapping, these erroneous parts will show up in the ultraproduct, and we are really interested only in parts stemming from the original operator. There are subspaces where these errors disappear, and one of them is
![]() $H^{Im}$
, which is canonical, as we have showed it to be isometrically isomorphic to H. A natural question arises:
$H^{Im}$
, which is canonical, as we have showed it to be isometrically isomorphic to H. A natural question arises:
Open question 3. Is there a natural characterization for the subspaces
![]() $H^m$
where the errors of the
$H^m$
where the errors of the
![]() $A_N$
’s disappear?
$A_N$
’s disappear?
As for the canonicity of our measure
![]() $\mu $
we have the following:
$\mu $
we have the following:
Corollary 3.14. The measure
![]() $\mu $
constructed is independent of the choice of cyclic vector. In particular all measures constructed in the above manner will agree on measure zero sets, and thus agree on which reals are nice.
$\mu $
constructed is independent of the choice of cyclic vector. In particular all measures constructed in the above manner will agree on measure zero sets, and thus agree on which reals are nice.
Proof. This follows from Corollary 3.10 and the uniqueness of the spectral measure (see, e.g., Section VII.2 of [Reference Reed and Simon9]).
However, note that in general
![]() $\sigma (A)\neq \sigma (A^m)$
, as the latter can be strictly larger. Thus we are not considering elementary embeddings into the (metric) ultraproduct, but only embeddings. This is enough for our purposes, as we only use the construction for calculating equations.
$\sigma (A)\neq \sigma (A^m)$
, as the latter can be strictly larger. Thus we are not considering elementary embeddings into the (metric) ultraproduct, but only embeddings. This is enough for our purposes, as we only use the construction for calculating equations.
4 Self-adjoint operators
In this section we show that the constructions from Sections 2 and 3 can be generalized to (bounded) self adjoint operators.
We will need the following facts, some of which seem hard to find in the literature (in particular item (iv) of the fact). Our version is not the best possible.
Fact 4.1. Let H be a separable Hilbert space and B a self-adjoint, U a unitary operator on H and I the identity operator.
-
(i)
 $\max \{\vert \lambda \vert \,\vert \, \lambda \in \sigma (B)\}=\Vert B\Vert $
,
$\max \{\vert \lambda \vert \,\vert \, \lambda \in \sigma (B)\}=\Vert B\Vert $
,
 $e^{iB}$
is unitary and
$e^{iB}$
is unitary and
 $\sigma (e^{iB})=\{e^{i\lambda } \vert \lambda \in \sigma (B)\}$
.
$\sigma (e^{iB})=\{e^{i\lambda } \vert \lambda \in \sigma (B)\}$
. -
(ii) Let r and q be reals.
 $e^{i(B+r I)}=e^{iB}\circ e^{ir}I$
,
$e^{i(B+r I)}=e^{iB}\circ e^{ir}I$
,
 $e^{iq}\in \sigma (e^{iB})$
iff
$e^{iq}\in \sigma (e^{iB})$
iff
 $e^{i(q +r)}\in \sigma (e^{i(B+r I)})$
and
$e^{i(q +r)}\in \sigma (e^{i(B+r I)})$
and
 $\lambda \in \sigma (B)$
iff
$\lambda \in \sigma (B)$
iff
 $\lambda +r\in \sigma (B+rI)$
.
$\lambda +r\in \sigma (B+rI)$
. -
(iii) Suppose
 $H_{0}$
is a complete subspace of H,
$H_{0}$
is a complete subspace of H,
 $H_{1}$
its orthogonal complement and
$H_{1}$
its orthogonal complement and
 $A_{i}$
are bounded operators on
$A_{i}$
are bounded operators on
 $H_{i}$
,
$H_{i}$
,
 $i<2$
. Then there is a unique operator A on H such that
$i<2$
. Then there is a unique operator A on H such that
 $A\restriction H_{i}=A_{i}$
for both
$A\restriction H_{i}=A_{i}$
for both
 $i<2$
and it is bounded and
$i<2$
and it is bounded and
 $\sigma (A)=\sigma (A_{0})\cup \sigma (A_{1})$
. If in addition both operators
$\sigma (A)=\sigma (A_{0})\cup \sigma (A_{1})$
. If in addition both operators
 $A_{i}$
are self-adjoint, then also A is self-adjoint and if both are unitary, then also A is unitary.
$A_{i}$
are self-adjoint, then also A is self-adjoint and if both are unitary, then also A is unitary. -
(iv) If
 $0\le r<\pi /2$
and for all
$0\le r<\pi /2$
and for all
 $\lambda \in \sigma (U)$
,
$\lambda \in \sigma (U)$
,
 $\lambda =e^{iq}$
for some
$\lambda =e^{iq}$
for some
 $q\in [{-}r,r]$
, then there is a unique self-adjoint operator A such that
$q\in [{-}r,r]$
, then there is a unique self-adjoint operator A such that
 $U=e^{i A}$
and
$U=e^{i A}$
and
 $\sigma (A)\subseteq [{-}r,r]$
.
$\sigma (A)\subseteq [{-}r,r]$
.
Proof. (i): The first claim is the spectral radius formula (for a proof see, e.g., Chapter VI of [Reference Reed and Simon9]) the others are proved via polynomial approximations, see Chapter VII of [Reference Reed and Simon9].
(ii): The first claim follows from the fact that B and
![]() $r I$
commute. The rest is easy.
$r I$
commute. The rest is easy.
(iii): Obviously A must be such that if
![]() $v\in H_{0}$
and
$v\in H_{0}$
and
![]() $u\in H_{1}$
, then
$u\in H_{1}$
, then
![]() $A(v+u)=A_{0}(v)+A_{1}(u)$
and this is a bounded operator. Also clearly
$A(v+u)=A_{0}(v)+A_{1}(u)$
and this is a bounded operator. Also clearly
![]() $\sigma (A_{0})\cup \sigma (A_{1})\subseteq \sigma (A)$
and since spectra are closed the other direction follows by an easy calculation. If
$\sigma (A_{0})\cup \sigma (A_{1})\subseteq \sigma (A)$
and since spectra are closed the other direction follows by an easy calculation. If
![]() $A_{0}$
and
$A_{0}$
and
![]() $A_{1}$
are self adjoint, then for all
$A_{1}$
are self adjoint, then for all
![]() $v_{0},v_{1}\in H_{0}$
and
$v_{0},v_{1}\in H_{0}$
and
![]() $u_{0},u_{1}\in H_{1}$
,
$u_{0},u_{1}\in H_{1}$
,
where the first and the third identity follow from the choice of
![]() $H_{0}$
and
$H_{0}$
and
![]() $H_{1}$
. Finally if
$H_{1}$
. Finally if
![]() $A_{0}$
and
$A_{0}$
and
![]() $A_{1}$
are unitary, easy calculations show that A is norm preserving and onto.
$A_{1}$
are unitary, easy calculations show that A is norm preserving and onto.
(iv): Let
![]() $U'=e^{i\pi }U$
. Then
$U'=e^{i\pi }U$
. Then
![]() $U'$
is unitary, and if
$U'$
is unitary, and if
![]() $\lambda \in \sigma (U')$
, then
$\lambda \in \sigma (U')$
, then
![]() $\lambda =e^{iq}$
for some
$\lambda =e^{iq}$
for some
![]() $q\in [{-}r+\pi ,r+\pi ]$
. Now by [Reference Stone11, Theorem 8.4], there is a unique self-adjoint operator
$q\in [{-}r+\pi ,r+\pi ]$
. Now by [Reference Stone11, Theorem 8.4], there is a unique self-adjoint operator
![]() $A'$
such that
$A'$
such that
![]() $U'=e^{i2\pi A'}$
and the spectrum of
$U'=e^{i2\pi A'}$
and the spectrum of
![]() $A'$
is a subset of
$A'$
is a subset of
![]() $[0,1]$
and 0 is not in the point spectrum of
$[0,1]$
and 0 is not in the point spectrum of
![]() $A'$
. By item (i), the spectrum of
$A'$
. By item (i), the spectrum of
![]() $2\pi A'$
is a subset of
$2\pi A'$
is a subset of
![]() $[\pi -r,\pi +r]$
. Let
$[\pi -r,\pi +r]$
. Let
![]() $A=2\pi A'-\pi I$
. Then
$A=2\pi A'-\pi I$
. Then
![]() $e^{iA}=U$
,
$e^{iA}=U$
,
![]() $\sigma (A)\subseteq [{-}r,r]$
and the uniqueness follows from the uniqueness of
$\sigma (A)\subseteq [{-}r,r]$
and the uniqueness follows from the uniqueness of
![]() $A'$
and (ii).
$A'$
and (ii).
From now on, in this section we assume that
![]() $Re(e^{i})\in NI$
. If this is not true, we can replace
$Re(e^{i})\in NI$
. If this is not true, we can replace
![]() $1$
by a real q close to
$1$
by a real q close to
![]() $1$
such that
$1$
such that
![]() $Re(e^{iq})\in NI$
and work with it.
$Re(e^{iq})\in NI$
and work with it.
Let B be a bounded self-adjoint operator on a separable Hilbert space H. It will turn out that it does not matter whether we look at B or
![]() $rB$
for some positive real r, and thus we may assume that the norm of B is
$rB$
for some positive real r, and thus we may assume that the norm of B is
![]() $\leq 1$
. Also we may assume that
$\leq 1$
. Also we may assume that
![]() $B(v)\ne 0$
for all
$B(v)\ne 0$
for all
![]() $v\in H-\{ 0\}$
because we can always restrict B to the orthogonal complement of its kernel (which is closed under B since B is self-adjoint). Let
$v\in H-\{ 0\}$
because we can always restrict B to the orthogonal complement of its kernel (which is closed under B since B is self-adjoint). Let
![]() $A=e^{iB}$
. Then A is unitary and not the identity by Fact 4.1. Also by the same fact, if
$A=e^{iB}$
. Then A is unitary and not the identity by Fact 4.1. Also by the same fact, if
![]() $\lambda \in \sigma (A)$
, then
$\lambda \in \sigma (A)$
, then
![]() $\lambda =e^{iq}$
for some
$\lambda =e^{iq}$
for some
![]() $q\in [-1,1]$
.
$q\in [-1,1]$
.
In the proof of the following lemma, the assumption that the norm of B is small plays an important role, stemming from Fact 4.1. We will need the uniqueness of the self-adjoint operator in point (iv) of the fact, and for that we need to avoid a ‘wraparound’. Our formulation of the fact allows for B to have norm smaller that
![]() $\pi /2$
, and we have chosen 1 as it is convenient in calculations.
$\pi /2$
, and we have chosen 1 as it is convenient in calculations.
Lemma 4.2. If
![]() $H_{0}$
is a complete subspace of H and closed under A and
$H_{0}$
is a complete subspace of H and closed under A and
![]() $A^{*}$
, then it is closed under B.
$A^{*}$
, then it is closed under B.
Proof. Suppose not. Let
![]() $H_{1}$
be the orthogonal complement of
$H_{1}$
be the orthogonal complement of
![]() $H_{0}$
in H. Then
$H_{0}$
in H. Then
![]() $H_{1}$
is closed under A and
$H_{1}$
is closed under A and
![]() $A^{*}$
and there are self-adjoint operators
$A^{*}$
and there are self-adjoint operators
![]() $B_{0}$
in
$B_{0}$
in
![]() $H_{0}$
and
$H_{0}$
and
![]() $B_{1}$
in
$B_{1}$
in
![]() $H_{1}$
such that
$H_{1}$
such that
![]() $e^{i B_{0}}=A\restriction H_{0}$
and
$e^{i B_{0}}=A\restriction H_{0}$
and
![]() $e^{i B_{1}}=A\restriction H_{1}$
. But then by Fact 4.1(iii) there is a self-adjoint operator
$e^{i B_{1}}=A\restriction H_{1}$
. But then by Fact 4.1(iii) there is a self-adjoint operator
![]() $B'$
in H such that
$B'$
in H such that
![]() $e^{i B'}=A$
(because
$e^{i B'}=A$
(because
![]() $e^{i B'}\restriction H_{0}=A\restriction H_{0}$
and
$e^{i B'}\restriction H_{0}=A\restriction H_{0}$
and
![]() $e^{i B'}\restriction H_{1}=A\restriction H_{1}$
and A is uniquely determined by
$e^{i B'}\restriction H_{1}=A\restriction H_{1}$
and A is uniquely determined by
![]() $A\restriction H_0$
and
$A\restriction H_0$
and
![]() $A\restriction H_1$
) and
$A\restriction H_1$
) and
![]() $B'\ne B$
. This contradicts Fact 4.1(iii).
$B'\ne B$
. This contradicts Fact 4.1(iii).
By Lemma 4.2, if we may assume that H has a cyclic vector with respect to the operator A as in Section 2, we have spaces
![]() $H_{N}$
, operators
$H_{N}$
, operators
![]() $A_{N}$
, functions G,
$A_{N}$
, functions G,
![]() $G^{m}$
,
$G^{m}$
,
![]() $F^m$
and
$F^m$
and
![]() $F_{N}$
, a spectral measure
$F_{N}$
, a spectral measure
![]() $\mu $
etc. as in sections 2 and 3. Notice that each
$\mu $
etc. as in sections 2 and 3. Notice that each
![]() $A_{N}$
is a unitary operator and thus for all
$A_{N}$
is a unitary operator and thus for all
![]() $N<{\omega }$
and
$N<{\omega }$
and
![]() $n< D_{N}$
,
$n< D_{N}$
,
![]() $\lambda _{N}(n)=e^{iq}$
for some
$\lambda _{N}(n)=e^{iq}$
for some
![]() $q\in ]-\pi ,\pi ]$
. It follows that
$q\in ]-\pi ,\pi ]$
. It follows that
![]() $\mu (S-S_{0})=0$
when
$\mu (S-S_{0})=0$
when
![]() $S_{0}$
is the set
$S_{0}$
is the set
![]() $\{ e^{iq}\vert \ q\in ]-\pi ,\pi ]\}$
.
$\{ e^{iq}\vert \ q\in ]-\pi ,\pi ]\}$
.
We define operators
![]() $B_{N}$
as follows:
$B_{N}$
as follows:
![]() $B_{N}(u_{N}(n))=qu_{N}(n)$
if
$B_{N}(u_{N}(n))=qu_{N}(n)$
if
![]() $A_{N}(u_{N}(n))=e^{iq}u_{N}(n)$
and
$A_{N}(u_{N}(n))=e^{iq}u_{N}(n)$
and
![]() $q\in ]-\pi ,\pi ]$
. We write
$q\in ]-\pi ,\pi ]$
. We write
![]() $B^{m}$
for the metric ultraproduct (with the filter
$B^{m}$
for the metric ultraproduct (with the filter
![]() ${\mathcal {U}}$
as in the previous sections) of the operators
${\mathcal {U}}$
as in the previous sections) of the operators
![]() $B_{N}$
. Then
$B_{N}$
. Then
![]() $A_{N}=e^{iB_{N}}$
for all
$A_{N}=e^{iB_{N}}$
for all
![]() $N<{\omega }$
and since the operators
$N<{\omega }$
and since the operators
![]() $B_{N}$
are uniformly bounded (by
$B_{N}$
are uniformly bounded (by
![]() $\pi $
) it is easy to see that
$\pi $
) it is easy to see that
![]() $A^{m}=e^{iB^{m}}$
. Also each
$A^{m}=e^{iB^{m}}$
. Also each
![]() $B_{N}$
is self-adjoint and thus also
$B_{N}$
is self-adjoint and thus also
![]() $B^{m}$
is self-adjoint. We want to show the following:
$B^{m}$
is self-adjoint. We want to show the following:
Theorem 4.3.
![]() $B^{m}\restriction H^{Im}=G^{m}B(G^{m})^{-1}$
.
$B^{m}\restriction H^{Im}=G^{m}B(G^{m})^{-1}$
.
This follows immediately from Fact 4.1(iv) if we know that
![]() $H^{Im}$
is closed under
$H^{Im}$
is closed under
![]() $B^{m}$
. So what we need to show is the following:
$B^{m}$
. So what we need to show is the following:
Lemma 4.4.
![]() $H^{Im}$
is closed under
$H^{Im}$
is closed under
![]() $B^{m}$
.
$B^{m}$
.
Proof. Suppose not. Note that from Corollaries 2.7 and 3.8 it follows that
![]() $H^{Im}:=rng(G^m)=rng(F^m)$
. Let
$H^{Im}:=rng(G^m)=rng(F^m)$
. Let
![]() $H_{0}$
be the closure of
$H_{0}$
be the closure of
![]() $H^{Im}$
under
$H^{Im}$
under
![]() $B^{m}$
i.e., the complete subspace of
$B^{m}$
i.e., the complete subspace of
![]() $H^{m}$
generated by the set
$H^{m}$
generated by the set
(keep in mind that
![]() $B^{m}$
is bounded). Then
$B^{m}$
is bounded). Then
![]() $H^m$
is a complete subspace of
$H^m$
is a complete subspace of
![]() $H_0$
, closed under
$H_0$
, closed under
![]() $A^m$
and
$A^m$
and
![]() $A^{m*}$
, so we get a contradiction as in the proof of Lemma 4.2, unless the norm is too large to guarantee uniqueness. But this we can rule out by showing the following:
$A^{m*}$
, so we get a contradiction as in the proof of Lemma 4.2, unless the norm is too large to guarantee uniqueness. But this we can rule out by showing the following:
Claim 4.4.1. The operator norm of
![]() $B^{m}\restriction H_{0}$
is
$B^{m}\restriction H_{0}$
is
![]() $\le 1$
.
$\le 1$
.
Proof. For a contradiction suppose that there is
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $k<{\omega }$
and
$k<{\omega }$
and
![]() $P\in \mathbb {C} [X,Y]$
such that
$P\in \mathbb {C} [X,Y]$
such that
![]() $\Vert B^{m}((B^{m})^{k}(F^m(f_{P})))\Vert>(1+\varepsilon )\Vert (B^{m})^{k}(F^m(f_{P}))\Vert $
. Since A is not the identity,
$\Vert B^{m}((B^{m})^{k}(F^m(f_{P})))\Vert>(1+\varepsilon )\Vert (B^{m})^{k}(F^m(f_{P}))\Vert $
. Since A is not the identity,
![]() $\mu (\{ 1\} )<1$
. So there are
$\mu (\{ 1\} )<1$
. So there are
![]() $\delta>0$
and
$\delta>0$
and
![]() $V\subseteq \sigma (A)$
such that
$V\subseteq \sigma (A)$
such that
![]() $\mu (V)>\delta $
, for all
$\mu (V)>\delta $
, for all
![]() $\lambda \in V$
,
$\lambda \in V$
,
![]() $\vert f_{P}(\lambda )\vert>\delta $
and if
$\vert f_{P}(\lambda )\vert>\delta $
and if
![]() $\lambda =e^{iq}\in V$
, then
$\lambda =e^{iq}\in V$
, then
![]() $\vert q\vert>\delta $
.
$\vert q\vert>\delta $
.
For all
![]() $N<{\omega }$
, let
$N<{\omega }$
, let
![]() $H^{0}_{N}$
be the subspace of
$H^{0}_{N}$
be the subspace of
![]() $H_{N}$
generated by those
$H_{N}$
generated by those
![]() $u_{N}(n)$
for which
$u_{N}(n)$
for which
![]() $\lambda _{N}(n)=e^{iq}$
for some
$\lambda _{N}(n)=e^{iq}$
for some
![]() $q\in [-\pi ,\pi ]$
such that
$q\in [-\pi ,\pi ]$
such that
![]() $\vert q\vert>1$
and let
$\vert q\vert>1$
and let
![]() $H^{1}_{N}$
be the subspace of
$H^{1}_{N}$
be the subspace of
![]() $H_{N}$
generated by those
$H_{N}$
generated by those
![]() $u_{N}(n)$
for which
$u_{N}(n)$
for which
![]() $\lambda _{N}(n)=e^{iq}$
for some
$\lambda _{N}(n)=e^{iq}$
for some
![]() $q\in [-\pi ,\pi ]$
such that
$q\in [-\pi ,\pi ]$
such that
![]() $\vert q\vert \le 1$
. Then
$\vert q\vert \le 1$
. Then
![]() $H^{1}_{N}$
is the orthogonal complement of
$H^{1}_{N}$
is the orthogonal complement of
![]() $H^{0}_{N}$
. Further let
$H^{0}_{N}$
. Further let
![]() $H^2_N$
be the subspace of
$H^2_N$
be the subspace of
![]() $H_N$
generated by those
$H_N$
generated by those
![]() $u_N(n)$
for which
$u_N(n)$
for which
![]() $\lambda _N(n)\in V$
. Let
$\lambda _N(n)\in V$
. Let
![]() $v_{i}(N)$
be the projection of
$v_{i}(N)$
be the projection of
![]() $F_{N}(f_{P})$
to
$F_{N}(f_{P})$
to
![]() $H^{i}_{N}$
,
$H^{i}_{N}$
,
![]() $i<3$
. Let
$i<3$
. Let
![]() $S^{*}$
be the set of all
$S^{*}$
be the set of all
![]() $\lambda \in S$
such that
$\lambda \in S$
such that
![]() $Re(\lambda )\ge Re(e^{i})$
. Notice that since
$Re(\lambda )\ge Re(e^{i})$
. Notice that since
![]() $Re(e^{i})\in NI$
(see the assumption immediately after the proof of Fact 4.1),
$Re(e^{i})\in NI$
(see the assumption immediately after the proof of Fact 4.1),
![]() $\mu (S^{*})$
and
$\mu (S^{*})$
and
![]() $\mu (S-S^{*})$
are ultralimits of
$\mu (S-S^{*})$
are ultralimits of
![]() $\mu _{N}(S^{*})$
and
$\mu _{N}(S^{*})$
and
![]() $\mu _{N}(S-S^{*})$
. Let s be the supremum of all
$\mu _{N}(S-S^{*})$
. Let s be the supremum of all
![]() $\vert f_{P}(\lambda )\vert $
for
$\vert f_{P}(\lambda )\vert $
for
![]() $\lambda \in S$
.
$\lambda \in S$
.
Now
-
(a)
in a set of N’s that belongs to $$ \begin{align*}&\lVert {(B_N)^k(F_N(f_P))}\rVert \geq \lVert {(B_N)^k(v_2(N))}\rVert =\\&\quad =\lVert{(B_N)^k\sum_{\lambda_N(n)\in V}\xi_N(n)f_P(\lambda_N(n))u_N(n)}\rVert\geq \delta^{k+3/2}\end{align*} $$
$$ \begin{align*}&\lVert {(B_N)^k(F_N(f_P))}\rVert \geq \lVert {(B_N)^k(v_2(N))}\rVert =\\&\quad =\lVert{(B_N)^k\sum_{\lambda_N(n)\in V}\xi_N(n)f_P(\lambda_N(n))u_N(n)}\rVert\geq \delta^{k+3/2}\end{align*} $$
 ${\mathcal {U}}$
,
${\mathcal {U}}$
,
-
(b)
in a set of N’s that belongs to $$ \begin{align*}&\lVert {B_N((B_N)^k(F_N(f_P)))}\rVert =\lVert {(B_N)^{k+1}(v_0(N)+v_1(N))}\rVert \leq\\&\quad\pi^{k+1}\sqrt{\mu_N(S-S^*)}s+\lVert{v_1(N)}\rVert\end{align*} $$
$$ \begin{align*}&\lVert {B_N((B_N)^k(F_N(f_P)))}\rVert =\lVert {(B_N)^{k+1}(v_0(N)+v_1(N))}\rVert \leq\\&\quad\pi^{k+1}\sqrt{\mu_N(S-S^*)}s+\lVert{v_1(N)}\rVert\end{align*} $$
 ${\mathcal {U}}$
,
${\mathcal {U}}$
,
-
(c)
 $\mu _{N}(S-S^{*})\le (\varepsilon \delta ^{k+3/2}/(2\pi ^{k+1}s))^{2}$
in a set of N’s that belong to
$\mu _{N}(S-S^{*})\le (\varepsilon \delta ^{k+3/2}/(2\pi ^{k+1}s))^{2}$
in a set of N’s that belong to
 ${\mathcal {U}}$
(since
${\mathcal {U}}$
(since
 $\mu (S-S^{*})=0$
by the assumption
$\mu (S-S^{*})=0$
by the assumption
 $\lVert {B}\rVert \leq 1$
and the construction of the measure for A).
$\lVert {B}\rVert \leq 1$
and the construction of the measure for A).
By putting these together, we get
in a set of N’s that belongs to
![]() ${\mathcal {U}}$
, which is a contradiction.
${\mathcal {U}}$
, which is a contradiction.
Now we can define an operator
![]() $B_{D}$
on
$B_{D}$
on
![]() $L_{2}(S,\mu )$
the natural way: For
$L_{2}(S,\mu )$
the natural way: For
![]() $f\in C(S)$
, we let
$f\in C(S)$
, we let
![]() $B_{D}(f)(\lambda )=K_B(\lambda )f(\lambda )$
, where
$B_{D}(f)(\lambda )=K_B(\lambda )f(\lambda )$
, where
![]() $K_B(\lambda )=q$
if
$K_B(\lambda )=q$
if
![]() $q\in ]-\pi ,\pi ]$
and
$q\in ]-\pi ,\pi ]$
and
![]() $\lambda =pe^{iq}$
for some real number p. Now it is easy to see that
$\lambda =pe^{iq}$
for some real number p. Now it is easy to see that
![]() $e^{iB_{D}}=A_{D}$
and thus by Fact 4.1,
$e^{iB_{D}}=A_{D}$
and thus by Fact 4.1,
![]() $B^{m}\restriction H^{Im}=F^m B_{D}(F^m)^{-1}$
.
$B^{m}\restriction H^{Im}=F^m B_{D}(F^m)^{-1}$
.
If we want for B exactly the same setup as for A we can do the following: Let
![]() ${S_{B}=]-\pi ,\pi ]}$
and define a Borel measure
${S_{B}=]-\pi ,\pi ]}$
and define a Borel measure
![]() $\mu _{B}$
on
$\mu _{B}$
on
![]() $S_{B}$
by letting
$S_{B}$
by letting
![]() $\mu _{B}(X)=\mu (K_{B}^{-1}(X))$
. Then we can define an operator
$\mu _{B}(X)=\mu (K_{B}^{-1}(X))$
. Then we can define an operator
![]() $B^{\prime }_{D}$
on
$B^{\prime }_{D}$
on
![]() $L_{2}(S_{B},\mu _{B})$
so that for all
$L_{2}(S_{B},\mu _{B})$
so that for all
![]() $f\in C(S_{B})$
,
$f\in C(S_{B})$
,
![]() $B^{\prime }_{D}(f)(q)=qf(q)$
. Finally we notice that if we define a continuous
$B^{\prime }_{D}(f)(q)=qf(q)$
. Finally we notice that if we define a continuous
![]() $F_{B}: L_{2}(S,\mu )\rightarrow L_{2}(S_{B},\mu _{B})$
so that for
$F_{B}: L_{2}(S,\mu )\rightarrow L_{2}(S_{B},\mu _{B})$
so that for
![]() $f\in C(S)$
,
$f\in C(S)$
,
![]() $F_{B}(f)(q)=f(e^{iq})$
we get an isometric isomorphism and
$F_{B}(f)(q)=f(e^{iq})$
we get an isometric isomorphism and
![]() $B^{\prime }_{D}=F_{B}B_{D}F_{B}^{-1}$
.
$B^{\prime }_{D}=F_{B}B_{D}F_{B}^{-1}$
.
5 Rigged Hilbert spaces
Rigged Hilbert spaces are a way of accounting for objects that don’t fit into a Hilbert space, such as Dirac delta functions. A rigged Hilbert space consists of a Hilbert space H and a subspace
![]() $\Phi $
(with a finer norm topology than the one given by the norm in H). One then has
$\Phi $
(with a finer norm topology than the one given by the norm in H). One then has
where
![]() $\Phi ^*$
is the dual space of
$\Phi ^*$
is the dual space of
![]() $\Phi $
. The elements in
$\Phi $
. The elements in
![]() $\Phi ^*$
are antilinear functionals, and if
$\Phi ^*$
are antilinear functionals, and if
![]() $\Phi $
was suitably chosen with respect to a cyclic, essentially self adjoint operator B, then the functionals act as generalized eigenvectors corresponding to values in the spectrum of B (see, e.g., [Reference de la Madrid Modino8]).
$\Phi $
was suitably chosen with respect to a cyclic, essentially self adjoint operator B, then the functionals act as generalized eigenvectors corresponding to values in the spectrum of B (see, e.g., [Reference de la Madrid Modino8]).
In this section we set out to find something similar to
![]() $\Phi ^*$
by considering different norms in our ultraproduct space
$\Phi ^*$
by considering different norms in our ultraproduct space
![]() $H^u$
, and finding extensions of
$H^u$
, and finding extensions of
![]() $H^{Im}$
. Here, as well as in the next section, it does not matter whether we look at a self-adjoint bounded B or
$H^{Im}$
. Here, as well as in the next section, it does not matter whether we look at a self-adjoint bounded B or
![]() $e^{iB}$
, and thus we return to the assumptions of sections 2 and 3, i.e., that A is bounded,
$e^{iB}$
, and thus we return to the assumptions of sections 2 and 3, i.e., that A is bounded,
![]() $A\circ A^{*}=A^{*}\circ A=r_{A}I$
and
$A\circ A^{*}=A^{*}\circ A=r_{A}I$
and
![]() $\phi $
is a cyclic vector. Also we let
$\phi $
is a cyclic vector. Also we let
![]() $H_{N}$
,
$H_{N}$
,
![]() $A_{N}$
etc. be as in these sections.
$A_{N}$
etc. be as in these sections.
We will look at two norms, that end up being essentially an
![]() $L_{\infty }$
-norm and an
$L_{\infty }$
-norm and an
![]() $L_{1}$
-norm. The latter of these will be called
$L_{1}$
-norm. The latter of these will be called
![]() $\Vert \cdot \Vert _{0}$
in order to avoid confusion. Strictly speaking both of these may be only seminorms in the finite dimensional spaces
$\Vert \cdot \Vert _{0}$
in order to avoid confusion. Strictly speaking both of these may be only seminorms in the finite dimensional spaces
![]() $H_{N}$
, but we will call them norms for simplicity. In the ultraproduct we will fraction out all vectors to which the seminorm gives an infinitesimal value, and then the seminorms become norms, and we obtain spaces
$H_{N}$
, but we will call them norms for simplicity. In the ultraproduct we will fraction out all vectors to which the seminorm gives an infinitesimal value, and then the seminorms become norms, and we obtain spaces
![]() $H^m_0$
and
$H^m_0$
and
![]() $H^m_\infty $
somewhat similarly to how we obtained
$H^m_\infty $
somewhat similarly to how we obtained
![]() $H^m$
for the
$H^m$
for the
![]() $\lVert {\cdot }\rVert _2$
-norm before. Then we will show how generalized distributions embed into
$\lVert {\cdot }\rVert _2$
-norm before. Then we will show how generalized distributions embed into
![]() $H^m_0$
such that values of the distribution can be calculated via a pairing function resembling an inner product.
$H^m_0$
such that values of the distribution can be calculated via a pairing function resembling an inner product.
Definition 5.1. Consider the following functions from
![]() $H_{N}$
to
$H_{N}$
to
![]() $\mathbb {C}$
: Let
$\mathbb {C}$
: Let
![]() $X\subseteq \mathbb {C}$
be a closed set such that
$X\subseteq \mathbb {C}$
be a closed set such that
![]() $X\subseteq S$
. Then
$X\subseteq S$
. Then
 $$ \begin{align*}\Vert\sum_{n=0}^{D_{N}-1}a_{n}u_N(n)\Vert^{X}_{\infty}=\sup\{\xi_{N}(n)^{-1}\vert a_{n}\vert\ \vert\ \lambda_{N}(n)\in X\} ,\end{align*} $$
$$ \begin{align*}\Vert\sum_{n=0}^{D_{N}-1}a_{n}u_N(n)\Vert^{X}_{\infty}=\sup\{\xi_{N}(n)^{-1}\vert a_{n}\vert\ \vert\ \lambda_{N}(n)\in X\} ,\end{align*} $$
where by
![]() $0^{-1}$
we mean
$0^{-1}$
we mean
![]() $0$
, and
$0$
, and
 $$ \begin{align*}\Vert\sum_{n=0}^{D_{N}-1}a_{n}u_N(n)\Vert_{0}=\sum_{n=0}^{D_{N}-1}\xi_{N}(n)\vert a_{n}\vert .\end{align*} $$
$$ \begin{align*}\Vert\sum_{n=0}^{D_{N}-1}a_{n}u_N(n)\Vert_{0}=\sum_{n=0}^{D_{N}-1}\xi_{N}(n)\vert a_{n}\vert .\end{align*} $$
Keep in mind that for all N and n,
![]() $\xi _{N}(n)$
is a non-negative real number
$\xi _{N}(n)$
is a non-negative real number
![]() $\le 1$
.
$\le 1$
.
We define the
![]() $\lVert {\cdot }\rVert ^X_\infty $
-norm this way to get something that corresponds to an
$\lVert {\cdot }\rVert ^X_\infty $
-norm this way to get something that corresponds to an
![]() $L_\infty $
-norm. When the map
$L_\infty $
-norm. When the map
![]() $F_N$
maps functions over S into vectors in
$F_N$
maps functions over S into vectors in
![]() $H_N$
, it carries with it a weight factor that needs to be removed in order to achieve this. And disregarding the values where
$H_N$
, it carries with it a weight factor that needs to be removed in order to achieve this. And disregarding the values where
![]() $\xi _N(n)=0$
corresponds to disregarding values in a set of measure 0.
$\xi _N(n)=0$
corresponds to disregarding values in a set of measure 0.
When constructing
![]() $H^m$
from the
$H^m$
from the
![]() $\lVert {\cdot }\rVert _2$
-norm we just fractioned out infinitesimals and discarded elements of infinite length. For our other norms we need to be a bit more careful. We start with
$\lVert {\cdot }\rVert _2$
-norm we just fractioned out infinitesimals and discarded elements of infinite length. For our other norms we need to be a bit more careful. We start with
![]() $\Vert \cdot \Vert _{0}$
. As with the Hilbert space norm, this gives first a function from
$\Vert \cdot \Vert _{0}$
. As with the Hilbert space norm, this gives first a function from
![]() $H^{u}$
to
$H^{u}$
to
![]() $\mathbb {C}^{u}$
, denoted by
$\mathbb {C}^{u}$
, denoted by
![]() $\Vert \cdot \Vert ^{u}_{0}$
. Note that the function is always defined, with values in a real closed field, but for some vectors the value may be
$\Vert \cdot \Vert ^{u}_{0}$
. Note that the function is always defined, with values in a real closed field, but for some vectors the value may be
![]() $>n$
for all natural numbers n. Further we get an equivalence relation on
$>n$
for all natural numbers n. Further we get an equivalence relation on
![]() $H^u$
by
$H^u$
by
![]() $v\sim _0w$
iff
$v\sim _0w$
iff
![]() $\lVert {v-w}\rVert ^u_0$
is infinitesimal.
$\lVert {v-w}\rVert ^u_0$
is infinitesimal.
Definition 5.2. Let
![]() $n<{\omega }$
,
$n<{\omega }$
,
![]() $Y\subseteq Sq_{n}$
,
$Y\subseteq Sq_{n}$
,
![]() $R^{Y}_{0}=\cup _{R\in Y}R$
,
$R^{Y}_{0}=\cup _{R\in Y}R$
,
![]() $S^{Y}_{0}=\cup _{R\in Y}\overline R$
,
$S^{Y}_{0}=\cup _{R\in Y}\overline R$
,
![]() $R^{Y}_{1}=\cup _{R\in Sq_{n}-Y}R$
and
$R^{Y}_{1}=\cup _{R\in Sq_{n}-Y}R$
and
![]() $S^{Y}_{1}=\cup _{R\in Sq_{n}-Y}\overline R$
. We say that Y is good if the distance between
$S^{Y}_{1}=\cup _{R\in Sq_{n}-Y}\overline R$
. We say that Y is good if the distance between
![]() $\sigma (A)$
and
$\sigma (A)$
and
![]() $S^{Y}_{1}$
is
$S^{Y}_{1}$
is
![]() $>0$
(then
$>0$
(then
![]() $\sigma (A)\subseteq S^{Y}_{0}$
). We say that
$\sigma (A)\subseteq S^{Y}_{0}$
). We say that
 $$ \begin{align*}(\sum_{k=0}^{D_{N}-1}a^{N}_{k}u_{N}(k))_{N<{\omega}}/{\mathcal{U}}\in H^{u}\end{align*} $$
$$ \begin{align*}(\sum_{k=0}^{D_{N}-1}a^{N}_{k}u_{N}(k))_{N<{\omega}}/{\mathcal{U}}\in H^{u}\end{align*} $$
(and
![]() $(\sum _{k=0}^{D_{N}-1}a^{N}_{k}u_{N}(k))_{N<{\omega }}$
) is
$(\sum _{k=0}^{D_{N}-1}a^{N}_{k}u_{N}(k))_{N<{\omega }}$
) is
![]() $0$
-good if for all good Y
$0$
-good if for all good Y
 $$ \begin{align*}(\sum_{\lambda_{N}(k)\in S^{Y}_{1}}\xi_{N}(k)\vert a^{N}_{k}\vert )_{N<{\omega}}/{\mathcal{U}}/\sim =0.\end{align*} $$
$$ \begin{align*}(\sum_{\lambda_{N}(k)\in S^{Y}_{1}}\xi_{N}(k)\vert a^{N}_{k}\vert )_{N<{\omega}}/{\mathcal{U}}/\sim =0.\end{align*} $$
Then we let
![]() $H^{m0}$
be the set of all
$H^{m0}$
be the set of all
![]() $0$
-good
$0$
-good
![]() $f/{\mathcal {U}}\in H^{u}$
such that
$f/{\mathcal {U}}\in H^{u}$
such that
![]() $\Vert f/{\mathcal {U}}\Vert ^{u}_{0}<n$
for some natural number n. And we let
$\Vert f/{\mathcal {U}}\Vert ^{u}_{0}<n$
for some natural number n. And we let
![]() $H^{m}_{0}=H^{m0}/\sim _{0}$
. Finally, we define the norm
$H^{m}_{0}=H^{m0}/\sim _{0}$
. Finally, we define the norm
![]() $\Vert \cdot \Vert _{0}$
on
$\Vert \cdot \Vert _{0}$
on
![]() $H^{m}_{0}$
as before:
$H^{m}_{0}$
as before:
![]() $\Vert f/{\mathcal {U}}/\sim _{0}\Vert _{0}=q$
if
$\Vert f/{\mathcal {U}}/\sim _{0}\Vert _{0}=q$
if
![]() $q\in \mathbb {C}$
is the unique element such that for all
$q\in \mathbb {C}$
is the unique element such that for all
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
With this norm
![]() $H^{m}_{0}$
is a Banach space (addition and scalar multiplication are defined as before). In order to simplify the notation, for all
$H^{m}_{0}$
is a Banach space (addition and scalar multiplication are defined as before). In order to simplify the notation, for all
![]() $f\in \Pi _{N\in {\omega }}H_{N}$
, we write
$f\in \Pi _{N\in {\omega }}H_{N}$
, we write
![]() $[f]_{0}=f/{\mathcal {U}}/\sim _{0}$
. Notice that if
$[f]_{0}=f/{\mathcal {U}}/\sim _{0}$
. Notice that if
![]() $f,g\in H^{u}$
and
$f,g\in H^{u}$
and
![]() $\Vert f-g\Vert ^{u}_{0}$
is infinitesimal and f is
$\Vert f-g\Vert ^{u}_{0}$
is infinitesimal and f is
![]() $0$
-good, then so is g. We also have the following:
$0$
-good, then so is g. We also have the following:
Lemma 5.3. For all
![]() $f\in C(S)$
,
$f\in C(S)$
,
![]() $F^u(f)\in H^{m0}$
and
$F^u(f)\in H^{m0}$
and
![]() $\Vert f\Vert _{1}=\Vert [F^u(f)]_{0}\Vert _{0}$
.
$\Vert f\Vert _{1}=\Vert [F^u(f)]_{0}\Vert _{0}$
.
Proof. For the first claim, note that
![]() $\mu (S)$
is bounded and, for a good Y,
$\mu (S)$
is bounded and, for a good Y,
![]() $\mu ^n(S^Y_1)=\mu (S^Y_1)=0$
, so as f is bounded,
$\mu ^n(S^Y_1)=\mu (S^Y_1)=0$
, so as f is bounded,
![]() $F^u(f)$
is 0-good and has bounded
$F^u(f)$
is 0-good and has bounded
![]() $\lVert {\cdot }\rVert ^u_0$
-norm.
$\lVert {\cdot }\rVert ^u_0$
-norm.
For the second claim, note that f is uniformly continuous and thus Riemann integrable, so we can for each
![]() $l<{\omega }$
and
$l<{\omega }$
and
![]() $X\in Sq_l$
pick any element
$X\in Sq_l$
pick any element
![]() $c_X\in X$
and then
$c_X\in X$
and then
On the other hand,
 $$ \begin{align*}\lVert{F^u(f)}\rVert^u_0=\lim_{N,{\mathcal{U}}}\sum_{k<D_N}\xi_N(k)^2\lvert{f(\lambda_N(k))}\rvert =\lim_{N,{\mathcal{U}}}\sum_{X\in Sq_l}\sum_{k<D_N,\lambda_N(k)\in X}\xi_N(k)^2\lvert{f(\lambda_N(k))}\rvert \end{align*} $$
$$ \begin{align*}\lVert{F^u(f)}\rVert^u_0=\lim_{N,{\mathcal{U}}}\sum_{k<D_N}\xi_N(k)^2\lvert{f(\lambda_N(k))}\rvert =\lim_{N,{\mathcal{U}}}\sum_{X\in Sq_l}\sum_{k<D_N,\lambda_N(k)\in X}\xi_N(k)^2\lvert{f(\lambda_N(k))}\rvert \end{align*} $$
for any l, and if l is large enough so that values of f differ only slightly within each
![]() $X\in Sq_l$
, we can replace all the eigenvalues within X with the
$X\in Sq_l$
, we can replace all the eigenvalues within X with the
![]() $c_X$
from above and have
$c_X$
from above and have
 $$ \begin{align*}\sum_{X\in Sq_l}\sum_{k<D_N,\lambda_N(k)\in X}\xi_N(k)^2\lvert{f(\lambda_N(k))}\rvert\approx \sum_{X\in Sq_l}\mu_N(X)\lvert{f(c_X)}\rvert. \end{align*} $$
$$ \begin{align*}\sum_{X\in Sq_l}\sum_{k<D_N,\lambda_N(k)\in X}\xi_N(k)^2\lvert{f(\lambda_N(k))}\rvert\approx \sum_{X\in Sq_l}\mu_N(X)\lvert{f(c_X)}\rvert. \end{align*} $$
For any l, we also have that for
![]() $X\in Sq_l$
,
$X\in Sq_l$
,
![]() $\mu (X)=\mu ^n(X)=\lim _{N,{\mathcal {U}}}\mu _N(X)$
.
$\mu (X)=\mu ^n(X)=\lim _{N,{\mathcal {U}}}\mu _N(X)$
.
So for any
![]() $\varepsilon>0$
, we can choose an l large enough to get (for all N).
$\varepsilon>0$
, we can choose an l large enough to get (for all N).
Let us then look at the norm
![]() $\Vert \cdot \Vert _{\infty }$
First we will need a modified version of the
$\Vert \cdot \Vert _{\infty }$
First we will need a modified version of the
![]() $\sup $
-norm on
$\sup $
-norm on
![]() $C(S)$
:
$C(S)$
:
Definition 5.4. We define a seminorm
![]() $\Vert f\Vert ^\sigma _{\infty }=\sup \{\vert f(\lambda )\vert \ \vert \ \lambda \in \sigma (A)\}$
on
$\Vert f\Vert ^\sigma _{\infty }=\sup \{\vert f(\lambda )\vert \ \vert \ \lambda \in \sigma (A)\}$
on
![]() $C(S)$
and write
$C(S)$
and write
![]() $L_{\infty }(S,\mu )$
for
$L_{\infty }(S,\mu )$
for
![]() $C(S)/\sim ^\sigma _{\infty }$
, where
$C(S)/\sim ^\sigma _{\infty }$
, where
![]() $f\sim ^\sigma _{\infty }g$
if
$f\sim ^\sigma _{\infty }g$
if
![]() $\Vert f-g\Vert ^\sigma _{\infty }=0$
.
$\Vert f-g\Vert ^\sigma _{\infty }=0$
.
Then
![]() $\Vert \cdot \Vert ^\sigma _{\infty }$
is a norm on
$\Vert \cdot \Vert ^\sigma _{\infty }$
is a norm on
![]() $L_{\infty }(S,\mu )$
.
$L_{\infty }(S,\mu )$
.
Definition 5.5. For all
![]() $\varepsilon>0$
, we let
$\varepsilon>0$
, we let
![]() $X_{\varepsilon }$
be the set of all
$X_{\varepsilon }$
be the set of all
![]() $\lambda \in \mathbb {C}$
whose distance to
$\lambda \in \mathbb {C}$
whose distance to
![]() $\sigma (A)$
is
$\sigma (A)$
is
![]() $\le \varepsilon $
and we let
$\le \varepsilon $
and we let
![]() $\Vert (v_{N})_{N<{\omega }}/{\mathcal {U}}\Vert ^{\varepsilon }_{\infty }$
be the unique
$\Vert (v_{N})_{N<{\omega }}/{\mathcal {U}}\Vert ^{\varepsilon }_{\infty }$
be the unique
![]() $q\in \mathbb {C}$
such that for all
$q\in \mathbb {C}$
such that for all
![]() $\delta>0$
$\delta>0$
if there is such a q and otherwise the value is
![]() $\infty $
(i.e., we do as before).
$\infty $
(i.e., we do as before).
Now let
![]() $v=(\sum _{k=0}^{D_{N}-1}a^{N}_{k}u_{N}(k))_{N<{\omega }}/{\mathcal {U}}\in H^{u}$
. Then we let
$v=(\sum _{k=0}^{D_{N}-1}a^{N}_{k}u_{N}(k))_{N<{\omega }}/{\mathcal {U}}\in H^{u}$
. Then we let
![]() $\Vert v\Vert _{\infty }=\lim _{\varepsilon \rightarrow 0}\Vert v\Vert ^{\varepsilon }_{\infty }$
if there are
$\Vert v\Vert _{\infty }=\lim _{\varepsilon \rightarrow 0}\Vert v\Vert ^{\varepsilon }_{\infty }$
if there are
![]() $p<{\omega }$
and
$p<{\omega }$
and
![]() $W\in {\mathcal {U}}$
for which
$W\in {\mathcal {U}}$
for which
![]() $\vert a^{N}_{k}(\xi _{N}(k))^{-1}\vert <p$
for all
$\vert a^{N}_{k}(\xi _{N}(k))^{-1}\vert <p$
for all
![]() $N\in W$
and
$N\in W$
and
![]() $k<D_{N}$
and otherwise we let
$k<D_{N}$
and otherwise we let
![]() $\Vert v\Vert _{\infty }=\infty $
. Notice that thus having bounded
$\Vert v\Vert _{\infty }=\infty $
. Notice that thus having bounded
![]() $\Vert \cdot \Vert _\infty $
-norm in
$\Vert \cdot \Vert _\infty $
-norm in
![]() $H^u$
requires the
$H^u$
requires the
![]() $\Vert \cdot \Vert ^S_\infty $
-norm to be bounded in a
$\Vert \cdot \Vert ^S_\infty $
-norm to be bounded in a
![]() ${\mathcal {U}}$
-large set of
${\mathcal {U}}$
-large set of
![]() $H_N$
s although the value is determined by what happens ‘close to
$H_N$
s although the value is determined by what happens ‘close to
![]() $\sigma (A)$
’. We then let
$\sigma (A)$
’. We then let
![]() $H^{m\infty }$
be the set of all
$H^{m\infty }$
be the set of all
![]() $v\in H^{u}$
for which
$v\in H^{u}$
for which
![]() $\Vert v\Vert _{\infty }<\infty $
and
$\Vert v\Vert _{\infty }<\infty $
and
![]() $H^{m}_{\infty }=H^{m\infty }/\sim _{\infty }$
, where
$H^{m}_{\infty }=H^{m\infty }/\sim _{\infty }$
, where
![]() $\sim _{\infty }$
is the relation
$\sim _{\infty }$
is the relation
![]() $\Vert v-u\Vert _{\infty }=0$
. We write
$\Vert v-u\Vert _{\infty }=0$
. We write
![]() $[f]_{\infty }$
for
$[f]_{\infty }$
for
![]() $f/{\mathcal {U}}/\sim _{\infty }$
.
$f/{\mathcal {U}}/\sim _{\infty }$
.
The definition above may seem cumbersome, as we cannot restrict attention to the spectrum directly. This is because, although our measure will find the right spectrum eventually (cf. Lemma 3.12), our construction does not give any direct control of this convergence. Each
![]() $H_N$
has a discrete spectrum, but it is not even guaranteed that the eigenvalues in
$H_N$
has a discrete spectrum, but it is not even guaranteed that the eigenvalues in
![]() $H_N$
are in
$H_N$
are in
![]() $\sigma (A)$
.
$\sigma (A)$
.
Lemma 5.6.
-
(i) For all
 $f\in C(S)$
,
$f\in C(S)$
,
 $F^u(f)\in H^{m\infty }$
and
$F^u(f)\in H^{m\infty }$
and
 $\Vert f\Vert ^\sigma _{\infty }=\Vert F^u(f)\Vert _{\infty }$
.
$\Vert f\Vert ^\sigma _{\infty }=\Vert F^u(f)\Vert _{\infty }$
. -
(ii) Every element of
 $H^{m\infty }$
has finite
$H^{m\infty }$
has finite
 $\lVert {\cdot }\rVert _2$
-norm, and for all
$\lVert {\cdot }\rVert _2$
-norm, and for all
 $v\in H^u$
,
$v\in H^u$
,
 $\lVert {v}\rVert ^u_0\leq \lVert {v}\rVert _2$
. For
$\lVert {v}\rVert ^u_0\leq \lVert {v}\rVert _2$
. For
 $f\in C(S)$
,
$f\in C(S)$
,
 $\lVert {F^u(f)}\rVert _0\leq \lVert {F^u(f)}\rVert _2\leq \lVert {F^u(f)}\rVert _\infty $
.
$\lVert {F^u(f)}\rVert _0\leq \lVert {F^u(f)}\rVert _2\leq \lVert {F^u(f)}\rVert _\infty $
.
Proof. (i) The first claim is clear since f is bounded. For the second, we notice that f is uniformly continuous and thus the direction
![]() $\Vert f\Vert ^\sigma _{\infty }\ge \Vert F^u(f)\Vert _{\infty }$
follows easily. The direction
$\Vert f\Vert ^\sigma _{\infty }\ge \Vert F^u(f)\Vert _{\infty }$
follows easily. The direction
![]() $\Vert f\Vert ^\sigma _{\infty }\le \Vert F^u(f)\Vert _{\infty }$
follows from the equality of
$\Vert f\Vert ^\sigma _{\infty }\le \Vert F^u(f)\Vert _{\infty }$
follows from the equality of
![]() $\sigma (A)$
and
$\sigma (A)$
and
![]() $\tilde {\sigma }(A)$
(recall Definition 3.11) and the continuity of f.
$\tilde {\sigma }(A)$
(recall Definition 3.11) and the continuity of f.
(ii) The first claim is a straightforward calculation, the second follows from Hölder’s inequality, as
![]() $\mu (S)=1$
. The chain of inequalities follows from the classical result.
$\mu (S)=1$
. The chain of inequalities follows from the classical result.
Let
![]() $H^{m}_{*}=\bigcup _{k\in \{ 0,2,\infty \}}H^{m}_{k}$
. We define a pairing
$H^{m}_{*}=\bigcup _{k\in \{ 0,2,\infty \}}H^{m}_{k}$
. We define a pairing
![]() $\langle \cdot |\cdot \rangle $
on
$\langle \cdot |\cdot \rangle $
on
![]() $H^{m}_{*}$
the same way as before: For
$H^{m}_{*}$
the same way as before: For
![]() $[f]_{k},[g]_{r}\in H^{m}_{*}$
,
$[f]_{k},[g]_{r}\in H^{m}_{*}$
,
![]() $\langle [f]_{k}|[g]_{r}\rangle =q$
if
$\langle [f]_{k}|[g]_{r}\rangle =q$
if
![]() $q\in \mathbb {C}$
is such that for all
$q\in \mathbb {C}$
is such that for all
![]() $f'\in [f]_{k}$
and
$f'\in [f]_{k}$
and
![]() $g'\in [g]_{r}$
,
$g'\in [g]_{r}$
,
![]() $\langle f'|g'\rangle ^{u}$
is infinitely close to q. If no such q exists we let
$\langle f'|g'\rangle ^{u}$
is infinitely close to q. If no such q exists we let
![]() $\langle [f]_{k}|[g]_{r}\rangle =\infty $
(meaning that
$\langle [f]_{k}|[g]_{r}\rangle =\infty $
(meaning that
![]() $\langle [f]_{k}|[g]_{r}\rangle $
is not well-defined).
$\langle [f]_{k}|[g]_{r}\rangle $
is not well-defined).
Lemma 5.7. If
![]() $x\in H^{m}_{\infty }$
and
$x\in H^{m}_{\infty }$
and
![]() $y\in H^{m}_{0}$
, then
$y\in H^{m}_{0}$
, then
![]() $\langle x|y\rangle \ne \infty $
.
$\langle x|y\rangle \ne \infty $
.
Proof. Let
![]() $x=[(x_{N})_{N<{\omega }}]_{\infty }$
, where
$x=[(x_{N})_{N<{\omega }}]_{\infty }$
, where
 $$ \begin{align*}x_{N}=\sum_{n=0}^{D_{N}-1}a^{N}_{n}u_{N}(n)\end{align*} $$
$$ \begin{align*}x_{N}=\sum_{n=0}^{D_{N}-1}a^{N}_{n}u_{N}(n)\end{align*} $$
and
![]() $y=[(y_{N})_{N<{\omega }}]_{0}$
, where
$y=[(y_{N})_{N<{\omega }}]_{0}$
, where
 $$ \begin{align*}y_{N}=\sum_{n=0}^{D_{N}-1}b^{N}_{n}u_{N}(n)\end{align*} $$
$$ \begin{align*}y_{N}=\sum_{n=0}^{D_{N}-1}b^{N}_{n}u_{N}(n)\end{align*} $$
and let
![]() $q>\Vert x\Vert _{\infty }$
and
$q>\Vert x\Vert _{\infty }$
and
![]() $r>\Vert y\Vert _{0}$
. Let
$r>\Vert y\Vert _{0}$
. Let
![]() $p<{\omega }$
, be such that for all
$p<{\omega }$
, be such that for all
![]() $N<{\omega }$
and
$N<{\omega }$
and
![]() $n<D_{N}$
,
$n<D_{N}$
,
![]() $\vert a^{N}_{n}(\xi _{N}(n))^{-1}\vert <p$
. It is enough to show that
$\vert a^{N}_{n}(\xi _{N}(n))^{-1}\vert <p$
. It is enough to show that
Let
![]() $\varepsilon>0$
be such that
$\varepsilon>0$
be such that
![]() $\Vert x\Vert ^{\varepsilon }_{\infty }<q$
. Then we choose
$\Vert x\Vert ^{\varepsilon }_{\infty }<q$
. Then we choose
![]() $k<{\omega }$
so that there is a good
$k<{\omega }$
so that there is a good
![]() $Y\subseteq Sq_{k}$
such that if as before we denote
$Y\subseteq Sq_{k}$
such that if as before we denote
![]() $S^{Y}_{0}=\cup _{R\in Y}\overline R$
and
$S^{Y}_{0}=\cup _{R\in Y}\overline R$
and
![]() $S^{Y}_{1}=\cup _{R\in Sq_{k}-Y}\overline R$
, then
$S^{Y}_{1}=\cup _{R\in Sq_{k}-Y}\overline R$
, then
![]() $S-X_{\varepsilon }\subseteq S^{Y}_{1}$
. Then
$S-X_{\varepsilon }\subseteq S^{Y}_{1}$
. Then
 $$ \begin{align*}\vert \langle x_{N}|y_{N}\rangle\vert\le\sum_{n=0}^{D_{N-1}}\vert a_{n}^{N}\vert\ \vert b^{N}_{n}\vert <\end{align*} $$
$$ \begin{align*}\vert \langle x_{N}|y_{N}\rangle\vert\le\sum_{n=0}^{D_{N-1}}\vert a_{n}^{N}\vert\ \vert b^{N}_{n}\vert <\end{align*} $$
 $$ \begin{align*}< \sum_{\lambda_{N}(n)\in S^{Y}_{0}}\xi_{N}(n)q\vert b^{N}_{n}\vert +\sum_{\lambda_{N}(n)\in S^{Y}_{1}}\xi_{N}(n)p\vert b^{N}_{n}\vert\le\end{align*} $$
$$ \begin{align*}< \sum_{\lambda_{N}(n)\in S^{Y}_{0}}\xi_{N}(n)q\vert b^{N}_{n}\vert +\sum_{\lambda_{N}(n)\in S^{Y}_{1}}\xi_{N}(n)p\vert b^{N}_{n}\vert\le\end{align*} $$
 $$ \begin{align*}\le q\sum_{\lambda_{N}(n)\in S^{Y}_{0}}\xi_{N}(n)\vert b^{N}_{n}\vert +p\sum_{\lambda_{N}(n)\in S^{Y}_{1}}\xi_{N}(n)\vert b^{N}_{n}\vert <qr +p\sum_{\lambda_{N}(n)\in S^{Y}_{1}}\xi_{N}(n)\vert b^{N}_{n}\vert\end{align*} $$
$$ \begin{align*}\le q\sum_{\lambda_{N}(n)\in S^{Y}_{0}}\xi_{N}(n)\vert b^{N}_{n}\vert +p\sum_{\lambda_{N}(n)\in S^{Y}_{1}}\xi_{N}(n)\vert b^{N}_{n}\vert <qr +p\sum_{\lambda_{N}(n)\in S^{Y}_{1}}\xi_{N}(n)\vert b^{N}_{n}\vert\end{align*} $$
in a set of
![]() $N<{\omega }$
that belongs to
$N<{\omega }$
that belongs to
![]() ${\mathcal {U}}$
. Now the claim follows from the assumption that
${\mathcal {U}}$
. Now the claim follows from the assumption that
![]() $(y_{N})_{N<{\omega }}/{\mathcal {U}}$
is
$(y_{N})_{N<{\omega }}/{\mathcal {U}}$
is
![]() $0$
-good.
$0$
-good.
Next we set out to find distributions as vectors in our space
![]() $H^u$
.
$H^u$
.
Definition 5.8. We say that an antilinear map
![]() $\theta :D(S)\rightarrow \mathbb {C}$
is a generalized distribution if it is bounded in the sense of
$\theta :D(S)\rightarrow \mathbb {C}$
is a generalized distribution if it is bounded in the sense of
![]() $\Vert \cdot \Vert ^\sigma _{\infty }$
, i.e., there is
$\Vert \cdot \Vert ^\sigma _{\infty }$
, i.e., there is
![]() $K<{\omega }$
such that
$K<{\omega }$
such that
![]() $\vert \theta (f)\vert \le K\Vert f\Vert ^\sigma _{\infty }$
. Then
$\vert \theta (f)\vert \le K\Vert f\Vert ^\sigma _{\infty }$
. Then
![]() $\theta $
extends to
$\theta $
extends to
![]() $C(S)$
by continuity and thus by generalized distributions we actually mean bounded antilinear maps
$C(S)$
by continuity and thus by generalized distributions we actually mean bounded antilinear maps
![]() $\theta :C(S)\rightarrow \mathbb {C}$
.
$\theta :C(S)\rightarrow \mathbb {C}$
.
We now fix a generalized distribution
![]() $\theta $
for the remainder of this section.
$\theta $
for the remainder of this section.
In general a distribution emerges through its test functions, and we will construct test functions picking out rectangles in the spectrum, similarly to how the measure was built. This will let us ‘copy over’ the values of
![]() $\theta $
to our vector. However, we need to be careful to make sure our rectangles are well behaved.
$\theta $
to our vector. However, we need to be careful to make sure our rectangles are well behaved.
Definition 5.9. We return to the lines
![]() $I_{r}$
and
$I_{r}$
and
![]() $J_{r}$
and to the sets
$J_{r}$
and to the sets
![]() $I_{r}^{\varepsilon }$
and
$I_{r}^{\varepsilon }$
and
![]() $J_{r}^{\varepsilon }$
from Section 3. For
$J_{r}^{\varepsilon }$
from Section 3. For
![]() $X\subseteq \mathbb {C}$
, we say that
$X\subseteq \mathbb {C}$
, we say that
![]() $f\in C(S)$
is an X-function if for all
$f\in C(S)$
is an X-function if for all
![]() $x\in S$
,
$x\in S$
,
![]() $\vert f(x)\vert \le 1$
and for all
$\vert f(x)\vert \le 1$
and for all
![]() $x\in S-X$
,
$x\in S-X$
,
![]() $f(x)=0$
. Notice that we do not require that
$f(x)=0$
. Notice that we do not require that
![]() $X\subseteq S$
but still
$X\subseteq S$
but still
![]() $dom(f)=S$
.
$dom(f)=S$
.
We say that a line
![]() $I_{r}$
is good (for
$I_{r}$
is good (for
![]() $\theta )$
if for all
$\theta )$
if for all
![]() $\delta>0$
there is
$\delta>0$
there is
![]() $\varepsilon>0$
such that for all
$\varepsilon>0$
such that for all
![]() $I^{\varepsilon }_{r}$
-functions f,
$I^{\varepsilon }_{r}$
-functions f,
![]() $\vert \theta (f)\vert <\delta $
.
$\vert \theta (f)\vert <\delta $
.
![]() $J_{r}$
being good is defined similarly.
$J_{r}$
being good is defined similarly.
Lemma 5.10. There are at most countably many
![]() $r\in [{-}M,M]$
such that
$r\in [{-}M,M]$
such that
![]() $I_{r}$
is not good, and the same is true for the lines
$I_{r}$
is not good, and the same is true for the lines
![]() $J_{r}$
.
$J_{r}$
.
Proof. Suppose not. Then there are
![]() $\delta>0$
and
$\delta>0$
and
![]() $r_{i}$
,
$r_{i}$
,
![]() $i<{\omega }_{1}$
, such that for all
$i<{\omega }_{1}$
, such that for all
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $i<{\omega }_{1}$
, there is an
$i<{\omega }_{1}$
, there is an
![]() $I^{\varepsilon }_{r_{i}}$
-function
$I^{\varepsilon }_{r_{i}}$
-function
![]() $f^{\varepsilon }_{i}$
such that
$f^{\varepsilon }_{i}$
such that
![]() $\vert \theta (f^{\varepsilon }_{i})\vert>\delta $
. W.l.o.g. we may assume that for all
$\vert \theta (f^{\varepsilon }_{i})\vert>\delta $
. W.l.o.g. we may assume that for all
![]() $i<{\omega }$
,
$i<{\omega }$
,
![]() $r_{i}<r_{i+1}$
. Then for all
$r_{i}<r_{i+1}$
. Then for all
![]() $i<{\omega }$
, we choose
$i<{\omega }$
, we choose
![]() $\varepsilon _{i}>0$
so that for all
$\varepsilon _{i}>0$
so that for all
![]() $i<{\omega }$
,
$i<{\omega }$
,
![]() $r_{i}+\varepsilon _{i}<r_{i+1}-\varepsilon _{i+1}$
. Also w.l.o.g. we may assume that for all
$r_{i}+\varepsilon _{i}<r_{i+1}-\varepsilon _{i+1}$
. Also w.l.o.g. we may assume that for all
![]() $i<{\omega }$
, the direction of
$i<{\omega }$
, the direction of
![]() $\lambda _{i}=\theta (f^{\varepsilon _{i}}_{i})$
is roughly the same, e.g.,
$\lambda _{i}=\theta (f^{\varepsilon _{i}}_{i})$
is roughly the same, e.g.,
![]() $Re(\lambda _{i})\ge Im(\lambda _{i})\ge 0$
. Let
$Re(\lambda _{i})\ge Im(\lambda _{i})\ge 0$
. Let
![]() $f=\sum _{i<{\omega }}(1/(i+1))f^{\varepsilon _{i}}_{i}$
. Clearly
$f=\sum _{i<{\omega }}(1/(i+1))f^{\varepsilon _{i}}_{i}$
. Clearly
![]() $f\in C(S)$
and
$f\in C(S)$
and
![]() $\Vert f\Vert _{\infty }\le 1$
but
$\Vert f\Vert _{\infty }\le 1$
but
![]() $\theta (f)=\infty $
, a contradiction.
$\theta (f)=\infty $
, a contradiction.
Definition 5.11. We say that
![]() $I_{r}$
is very good (for
$I_{r}$
is very good (for
![]() $\theta )$
if it is good and for all
$\theta )$
if it is good and for all
![]() $\delta>0$
, there is
$\delta>0$
, there is
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $\mu ^{n}(I^{\varepsilon }_{r})<\delta $
.
$\mu ^{n}(I^{\varepsilon }_{r})<\delta $
.
![]() $J_{r}$
being very good is defined similarly. We say that
$J_{r}$
being very good is defined similarly. We say that
![]() $\varepsilon>0$
is nice for r if both
$\varepsilon>0$
is nice for r if both
![]() $r-\varepsilon $
and
$r-\varepsilon $
and
![]() $r+\varepsilon $
are nice or
$r+\varepsilon $
are nice or
![]() ${<}{-}\,M$
or
${<}{-}\,M$
or
![]() $>M$
.
$>M$
.
Lemma 5.12.
-
(i) There are at most countably many
 $r\in [{-}M,M]$
such that
$r\in [{-}M,M]$
such that
 $I_{r}$
is not very good and the same is true for lines
$I_{r}$
is not very good and the same is true for lines
 $J_{r}$
.
$J_{r}$
. -
(ii) For all r there are at most countably many
 $\varepsilon>0$
that are not nice for r.
$\varepsilon>0$
that are not nice for r. -
(iii) If
 $\varepsilon>0$
is nice for r, then
$\varepsilon>0$
is nice for r, then
 $\mu (I_{r}^{\varepsilon })=\mu ^{n}(I_{r}^{\varepsilon })$
and
$\mu (I_{r}^{\varepsilon })=\mu ^{n}(I_{r}^{\varepsilon })$
and
 $\mu (J_{r}^{\varepsilon })=\mu ^{n}(J_{r}^{\varepsilon })$
.
$\mu (J_{r}^{\varepsilon })=\mu ^{n}(J_{r}^{\varepsilon })$
.
Proof. (ii): This is immediate by Lemma 3.2.
(i): This is immediate by Lemmas 3.2 and 5.10.
(iii): This can be proved as Lemma 3.4(i) was proved.
Definition 5.13. For all
![]() $k<{\omega }$
, we choose
$k<{\omega }$
, we choose
![]() $r^{k}_{i}\in [{-}M,M]$
,
$r^{k}_{i}\in [{-}M,M]$
,
![]() $i<2^{k+2}+1$
, so that:
$i<2^{k+2}+1$
, so that:
-
(i)
 $r^{k}_{i}<r^{k}_{i+1}$
and
$r^{k}_{i}<r^{k}_{i+1}$
and
 $r_{i+1}^{k}-r^{k}_{i}<2M/(k+1)$
,
$r_{i+1}^{k}-r^{k}_{i}<2M/(k+1)$
, -
(ii)
 $I_{r^{k}_{i}}$
and
$I_{r^{k}_{i}}$
and
 $J_{r^{k}_{i}}$
are very good for
$J_{r^{k}_{i}}$
are very good for
 $\theta $
,
$\theta $
, -
(iii)
 $r^{0}_{0}\,{=}\,{-}M$
and
$r^{0}_{0}\,{=}\,{-}M$
and
 $r^{0}_{4}=M$
,
$r^{0}_{4}=M$
, -
(iv) for all
 $i<2^{k+2}+1$
there is
$i<2^{k+2}+1$
there is
 $j<2^{k+3}+1$
such that
$j<2^{k+3}+1$
such that
 $r^{k}_{i}=r^{k+1}_{j}$
.
$r^{k}_{i}=r^{k+1}_{j}$
.
When we talk about
![]() $I^{\varepsilon }_{r^{k}_{i}}$
or
$I^{\varepsilon }_{r^{k}_{i}}$
or
![]() $J^{\varepsilon }_{r^{k}_{i}}$
we assume that
$J^{\varepsilon }_{r^{k}_{i}}$
we assume that
![]() $\varepsilon $
is small enough so that for all
$\varepsilon $
is small enough so that for all
![]() $j<2^{k+2}$
,
$j<2^{k+2}$
,
![]() $r^{k}_{j}+\varepsilon <r^{k}_{j+1}-\varepsilon $
.
$r^{k}_{j}+\varepsilon <r^{k}_{j+1}-\varepsilon $
.
For all
![]() $k<{\omega }$
,
$k<{\omega }$
,
![]() $i,j<2^{k+2}$
and
$i,j<2^{k+2}$
and
![]() $\varepsilon>0$
, we let
$\varepsilon>0$
, we let
![]() $B^{k}_{ij}=\{ \lambda \in S\vert \ r^{k}_{i}<Re(\lambda )<r^{k}_{i+1},\ r^{k}_{j}<Im(\lambda )<r^{k}_{j+1}\}$
and
$B^{k}_{ij}=\{ \lambda \in S\vert \ r^{k}_{i}<Re(\lambda )<r^{k}_{i+1},\ r^{k}_{j}<Im(\lambda )<r^{k}_{j+1}\}$
and
![]() $R^{k}_{\varepsilon }=\cup _{i<2^{k+2}+1}(I^{\varepsilon }_{r^k_{i}}\cup J^{\varepsilon }_{r^k_{i}})$
. We say that
$R^{k}_{\varepsilon }=\cup _{i<2^{k+2}+1}(I^{\varepsilon }_{r^k_{i}}\cup J^{\varepsilon }_{r^k_{i}})$
. We say that
![]() $\varepsilon>0$
is very nice for
$\varepsilon>0$
is very nice for
![]() $k<{\omega }$
, if it is nice for every
$k<{\omega }$
, if it is nice for every
![]() $r^k_{i}$
,
$r^k_{i}$
,
![]() $i<2^{k+2}$
. As in Lemma 5.12, we can see that
$i<2^{k+2}$
. As in Lemma 5.12, we can see that
![]() $\mu (B^{k}_{ij})=\mu ^{n}(B^{k}_{ij})$
, that if
$\mu (B^{k}_{ij})=\mu ^{n}(B^{k}_{ij})$
, that if
![]() $\varepsilon $
is very nice for k, then
$\varepsilon $
is very nice for k, then
![]() $\mu (R^{k}_{\varepsilon })=\mu ^{n}(R^{k}_{\varepsilon })$
, and that excluding countably many
$\mu (R^{k}_{\varepsilon })=\mu ^{n}(R^{k}_{\varepsilon })$
, and that excluding countably many
![]() $\varepsilon $
, every
$\varepsilon $
, every
![]() $\varepsilon $
is very nice for k.
$\varepsilon $
is very nice for k.
Lemma 5.14. For all
![]() $k<{\omega }$
and
$k<{\omega }$
and
![]() $\delta>0$
, there is
$\delta>0$
, there is
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $\mu (R^{k}_{\varepsilon })<\delta $
and for all
$\mu (R^{k}_{\varepsilon })<\delta $
and for all
![]() $R^{k}_{\varepsilon }$
-functions f,
$R^{k}_{\varepsilon }$
-functions f,
![]() $\vert \theta (f)\vert <\delta $
.
$\vert \theta (f)\vert <\delta $
.
Proof. For all
![]() $R^{k}_{\varepsilon }$
-functions f there are
$R^{k}_{\varepsilon }$
-functions f there are
![]() $I^{\varepsilon }_{r^{k}_{i}}$
- and
$I^{\varepsilon }_{r^{k}_{i}}$
- and
![]() $J^{\varepsilon }_{r^{k}_{i}}$
-functions
$J^{\varepsilon }_{r^{k}_{i}}$
-functions
![]() $f_{i}$
and
$f_{i}$
and
![]() $g_{i}$
,
$g_{i}$
,
![]() $i<2^{k+2}$
, such that
$i<2^{k+2}$
, such that
![]() $f=\sum _{i<2^{k+2}}(f_{i}+g_{i})$
. The only nontrivial part here are the ‘crossings’ between I and J lines, and there one can define
$f=\sum _{i<2^{k+2}}(f_{i}+g_{i})$
. The only nontrivial part here are the ‘crossings’ between I and J lines, and there one can define
![]() $f_i$
to be any continuous continuation from the values it has on the upper and lower edge of the crossing and 0 on the left and right edge, and define g from the differences
$f_i$
to be any continuous continuation from the values it has on the upper and lower edge of the crossing and 0 on the left and right edge, and define g from the differences
![]() $f-f_i$
. Then the claim follows easily.
$f-f_i$
. Then the claim follows easily.
Definition 5.15. For all
![]() $\lambda \in \mathbb {C}$
,
$\lambda \in \mathbb {C}$
,
![]() $k<{\omega }$
,
$k<{\omega }$
,
![]() $i,j<2^{k+2}$
and
$i,j<2^{k+2}$
and
![]() $\varepsilon>0$
, we choose a
$\varepsilon>0$
, we choose a
![]() $B^{k}_{i,j}$
-function
$B^{k}_{i,j}$
-function
![]() $f^{k\varepsilon \lambda }_{ij}$
so that for all
$f^{k\varepsilon \lambda }_{ij}$
so that for all
![]() $x\in \mathbb {C}$
, if
$x\in \mathbb {C}$
, if
![]() $r^{k}_{i}+\varepsilon <Re(x)<r^{k}_{i+1}-\varepsilon $
and
$r^{k}_{i}+\varepsilon <Re(x)<r^{k}_{i+1}-\varepsilon $
and
![]() $r^{k}_{j}+\varepsilon <Im(x)<r^{k}_{j+1}-\varepsilon $
, then
$r^{k}_{j}+\varepsilon <Im(x)<r^{k}_{j+1}-\varepsilon $
, then
![]() $f^{k\varepsilon \lambda }_{ij}(x)=\lambda $
. We then define
$f^{k\varepsilon \lambda }_{ij}(x)=\lambda $
. We then define
![]() $\theta (B^{k}_{ij},\lambda )$
to be
$\theta (B^{k}_{ij},\lambda )$
to be
![]() $\lim _{\varepsilon \rightarrow 0}\theta (f^{k\varepsilon \lambda }_{ij})$
. Notice that this does not depend on the choice of functions
$\lim _{\varepsilon \rightarrow 0}\theta (f^{k\varepsilon \lambda }_{ij})$
. Notice that this does not depend on the choice of functions
![]() $f^{k\varepsilon \lambda }_{ij}$
. Notice also that
$f^{k\varepsilon \lambda }_{ij}$
. Notice also that
![]() $\theta (B^{k}_{ij},\lambda )=\overline \lambda \theta (B^{k}_{i,j},1)$
.
$\theta (B^{k}_{ij},\lambda )=\overline \lambda \theta (B^{k}_{i,j},1)$
.
Definition 5.16. Suppose
![]() $n:{\omega }\rightarrow {\omega }$
and
$n:{\omega }\rightarrow {\omega }$
and
![]() $\varepsilon :{\omega }\rightarrow \mathbb {R}_{+}$
. We say that the pair
$\varepsilon :{\omega }\rightarrow \mathbb {R}_{+}$
. We say that the pair
![]() $(n,\varepsilon )$
is
$(n,\varepsilon )$
is
![]() $\theta $
-good if the following holds:
$\theta $
-good if the following holds:
-
(i) For all
 $0<m<{\omega }$
,
$0<m<{\omega }$
,
 $\{ N<{\omega }\vert \ n(N)>m,\ \varepsilon (N)<1/m\}\in {\mathcal {U}}$
.
$\{ N<{\omega }\vert \ n(N)>m,\ \varepsilon (N)<1/m\}\in {\mathcal {U}}$
. -
(ii) There is a
 $W=W(\theta ,n,\varepsilon )\in {\mathcal {U}}$
such that for all
$W=W(\theta ,n,\varepsilon )\in {\mathcal {U}}$
such that for all
 $N\in W$
if
$N\in W$
if
 $n=n(N)>0$
, then the following holds: Let
$n=n(N)>0$
, then the following holds: Let
 $\varepsilon =\varepsilon (N)>0$
,
$\varepsilon =\varepsilon (N)>0$
,
 $\delta '=\delta '(N)=\min \{ \mu _{N}(B^{n}_{ij})\vert \ i,j<2^{n+2},\ \mu (B^{n}_{ij})>0\}$
where
$\delta '=\delta '(N)=\min \{ \mu _{N}(B^{n}_{ij})\vert \ i,j<2^{n+2},\ \mu (B^{n}_{ij})>0\}$
where
 $\mu _{N}(B^{n}_{ij})=\sum _{\lambda _{N}(k)\in B^{n}_{ij}}\xi _{N}(k)^{2}$
, and let
$\mu _{N}(B^{n}_{ij})=\sum _{\lambda _{N}(k)\in B^{n}_{ij}}\xi _{N}(k)^{2}$
, and let
 $\delta =\delta (N)=\delta '/(2^{3(n+2)})$
. Then:
$\delta =\delta (N)=\delta '/(2^{3(n+2)})$
. Then:-
(a) for all
 $R^{n}_{\varepsilon }$
-functions f,
$R^{n}_{\varepsilon }$
-functions f,
 $\vert \theta (f)\vert <\delta $
,
$\vert \theta (f)\vert <\delta $
, -
(b)
 $\sum _{\lambda _{N}(i)\in R^{n}_{\varepsilon }}\xi _{N}(i)^{2}<\delta $
,
$\sum _{\lambda _{N}(i)\in R^{n}_{\varepsilon }}\xi _{N}(i)^{2}<\delta $
, -
(c) for all
 $i,j <2^{n+2}$
,
$i,j <2^{n+2}$
,
 $\vert \mu _{N}(B^{n}_{ij})-\mu (B^{n}_{ij})\vert <\delta $
.
$\vert \mu _{N}(B^{n}_{ij})-\mu (B^{n}_{ij})\vert <\delta $
.
-
-
(iii)
 $\varepsilon (N)$
is very nice for
$\varepsilon (N)$
is very nice for
 $n(N)$
.
$n(N)$
.
Notice that if
![]() $(n,\varepsilon )$
is
$(n,\varepsilon )$
is
![]() $\theta $
-good and for all
$\theta $
-good and for all
![]() $N<{\omega }$
,
$N<{\omega }$
,
![]() $0<\varepsilon ' (N)<\varepsilon (N)$
, and
$0<\varepsilon ' (N)<\varepsilon (N)$
, and
![]() $\varepsilon '$
is very nice for
$\varepsilon '$
is very nice for
![]() $n(N)$
, then
$n(N)$
, then
![]() $(n,\varepsilon ')$
is
$(n,\varepsilon ')$
is
![]() $\theta $
-good. So keeping in mind that the set of
$\theta $
-good. So keeping in mind that the set of
![]() $\varepsilon $
very nice for n is dense, we can always assume, e.g., that
$\varepsilon $
very nice for n is dense, we can always assume, e.g., that
![]() $\varepsilon (N)$
is such that for all
$\varepsilon (N)$
is such that for all
![]() $i<2^{n(N)+2}$
,
$i<2^{n(N)+2}$
,
![]() $\varepsilon (N)<(r^{n(N)}_{i+1}-r^{n(N)}_{i})/3$
.
$\varepsilon (N)<(r^{n(N)}_{i+1}-r^{n(N)}_{i})/3$
.
Lemma 5.17. There is a
![]() $\theta $
-good pair
$\theta $
-good pair
![]() $(n,\varepsilon )$
for which we can choose
$(n,\varepsilon )$
for which we can choose
![]() $W(\theta ,n,\varepsilon )={\omega }$
.
$W(\theta ,n,\varepsilon )={\omega }$
.
Proof. Simply let
![]() $n(N)$
be the largest natural number
$n(N)$
be the largest natural number
![]() $0<n\le N$
for which there is
$0<n\le N$
for which there is
![]() $\varepsilon =\varepsilon (N)$
for which Definition 5.16(ii) and (iii) hold, if such n and
$\varepsilon =\varepsilon (N)$
for which Definition 5.16(ii) and (iii) hold, if such n and
![]() $\varepsilon $
exist and otherwise we let
$\varepsilon $
exist and otherwise we let
![]() $n(N)=0$
and
$n(N)=0$
and
![]() $\varepsilon =1$
. Since for all
$\varepsilon =1$
. Since for all
![]() $\delta>0$
,
$\delta>0$
,
![]() $n<{\omega }$
and
$n<{\omega }$
and
![]() $i,j<2^{n+2}$
, the set
$i,j<2^{n+2}$
, the set
belongs to
![]() ${\mathcal {U}}$
, it is easy to see that now also (i) holds.
${\mathcal {U}}$
, it is easy to see that now also (i) holds.
Remark 5.18. The reader may wonder what the purpose of the sets
![]() $W(\theta ,n,\varepsilon )$
is. In the context when we have infinitely many generalized distributions
$W(\theta ,n,\varepsilon )$
is. In the context when we have infinitely many generalized distributions
![]() $\theta $
to handle, we need to diagonalize and then these sets become handy, see Remarks 5.22 and 6.5.
$\theta $
to handle, we need to diagonalize and then these sets become handy, see Remarks 5.22 and 6.5.
Now we fix a
![]() $\theta $
-good pair
$\theta $
-good pair
![]() $(n,\varepsilon )$
and in order to simplify the notations, we assume that
$(n,\varepsilon )$
and in order to simplify the notations, we assume that
![]() $W(\theta ,n,\varepsilon )={\omega }$
.
$W(\theta ,n,\varepsilon )={\omega }$
.
We are finally ready to define the vector in
![]() $H^u$
that will correspond to the distribution
$H^u$
that will correspond to the distribution
![]() $\theta $
:
$\theta $
:
Definition 5.19. We define
![]() $u(\theta )=(u_{N}(\theta ))_{N<{\omega }}/{\mathcal {U}}\in H^{u}$
by letting
$u(\theta )=(u_{N}(\theta ))_{N<{\omega }}/{\mathcal {U}}\in H^{u}$
by letting
![]() $n=n(N)$
and defining
$n=n(N)$
and defining
 $$ \begin{align*}u_{N}(\theta )=\sum_{\mu (B^{n}_{ij})\ne 0}\sum_{\lambda_{N}(k)\in B^{n}_{ij}}(\xi_{N}(k)\theta (B^{n}_{ij},1)/\mu_{N}(B^{n}_{ij}))u_{N}(k).\end{align*} $$
$$ \begin{align*}u_{N}(\theta )=\sum_{\mu (B^{n}_{ij})\ne 0}\sum_{\lambda_{N}(k)\in B^{n}_{ij}}(\xi_{N}(k)\theta (B^{n}_{ij},1)/\mu_{N}(B^{n}_{ij}))u_{N}(k).\end{align*} $$
Recall that we may assume the relevant
![]() $\mu _N(B^n_{ij})\neq 0$
, as this will happen for all N in some
$\mu _N(B^n_{ij})\neq 0$
, as this will happen for all N in some
![]() $W\in {\mathcal {U}}$
. Also notice that
$W\in {\mathcal {U}}$
. Also notice that
![]() $u(\theta )$
is
$u(\theta )$
is
![]() $0$
-good (immediate by the definition) and that for all
$0$
-good (immediate by the definition) and that for all
![]() $f\in C(S)$
, one can define a generalized distribution
$f\in C(S)$
, one can define a generalized distribution
![]() $\theta _{f}$
by
$\theta _{f}$
by
![]() $\theta _{f}(g)=\langle g|f\rangle $
and then (if
$\theta _{f}(g)=\langle g|f\rangle $
and then (if
![]() $\theta =\theta _{f}$
)
$\theta =\theta _{f}$
)
![]() $[F^u(f)]_{0}=[u(\theta _{f})]_{0}$
(easy calculation).
$[F^u(f)]_{0}=[u(\theta _{f})]_{0}$
(easy calculation).
Lemma 5.20.
![]() $\Vert u(\theta )\Vert _{0}<\infty $
.
$\Vert u(\theta )\Vert _{0}<\infty $
.
Proof. Let K be such that for all
![]() $f\in C(S)$
,
$f\in C(S)$
,
![]() $\vert \theta (f)\vert <K\Vert f\Vert ^\sigma _{\infty }$
. It is enough to show that for all
$\vert \theta (f)\vert <K\Vert f\Vert ^\sigma _{\infty }$
. It is enough to show that for all
![]() $N<{\omega }$
,
$N<{\omega }$
,
 $$ \begin{align*}\sum_{\mu (B^{n}_{ij})\ne 0}\sum_{\lambda_{N}(k)\in B^{n}_{ij}}\vert\xi_{N}(k)^{2}\theta (B^{n}_{ij},1)/\mu_{N}(B^{n}_{ij})\vert =\end{align*} $$
$$ \begin{align*}\sum_{\mu (B^{n}_{ij})\ne 0}\sum_{\lambda_{N}(k)\in B^{n}_{ij}}\vert\xi_{N}(k)^{2}\theta (B^{n}_{ij},1)/\mu_{N}(B^{n}_{ij})\vert =\end{align*} $$
 $$ \begin{align*}\sum_{\mu (B^{n}_{ij})\ne 0}\vert\theta (B^{n}_{ij},1)\vert\le 16K,\end{align*} $$
$$ \begin{align*}\sum_{\mu (B^{n}_{ij})\ne 0}\vert\theta (B^{n}_{ij},1)\vert\le 16K,\end{align*} $$
where
![]() $n=n(N)$
. Suppose not. Then one can find
$n=n(N)$
. Suppose not. Then one can find
![]() $X\subseteq \{ B^{n}_{ij}\vert \ i,j<2^{n+2},\ \mu (B^{n}_{ij})>0\}$
such that
$X\subseteq \{ B^{n}_{ij}\vert \ i,j<2^{n+2},\ \mu (B^{n}_{ij})>0\}$
such that
and for all
![]() $B\in X$
,
$B\in X$
,
![]() $\theta (B,1)$
point roughly to the same direction, e.g.,
$\theta (B,1)$
point roughly to the same direction, e.g.,
![]() $Re(\theta (B,1))\ge Im(\theta (B,1))\ge 0$
, see the proof of Lemma 5.10. But now for all
$Re(\theta (B,1))\ge Im(\theta (B,1))\ge 0$
, see the proof of Lemma 5.10. But now for all
![]() $B\in X$
, choose a B-function
$B\in X$
, choose a B-function
![]() $f_{B}$
so that
$f_{B}$
so that
![]() $\theta (B,1)$
is very close to
$\theta (B,1)$
is very close to
![]() $\theta (f_{B})$
. Let
$\theta (f_{B})$
. Let
![]() $f=\sum _{B\in X}f_{B}\in C(S)$
. Then
$f=\sum _{B\in X}f_{B}\in C(S)$
. Then
![]() $\Vert f\Vert _{\infty }=1$
but
$\Vert f\Vert _{\infty }=1$
but
![]() $\vert \theta (f)\vert>K$
, a contradiction.
$\vert \theta (f)\vert>K$
, a contradiction.
Theorem 5.21. For all
![]() $f\in C(S)$
,
$f\in C(S)$
,
![]() $\theta (f)=\langle [F^u(f)]_{\infty }|[u(\theta )]_{0}\rangle $
.
$\theta (f)=\langle [F^u(f)]_{\infty }|[u(\theta )]_{0}\rangle $
.
Proof. Let
![]() $f\in C(S)$
. W.l.o.g. we may assume that
$f\in C(S)$
. W.l.o.g. we may assume that
![]() $\vert f(x)\vert \le 1$
for all
$\vert f(x)\vert \le 1$
for all
![]() $x\in S$
, in particular,
$x\in S$
, in particular,
![]() $\Vert f\Vert ^\sigma _{\infty }\le 1$
. For all
$\Vert f\Vert ^\sigma _{\infty }\le 1$
. For all
![]() $0<n<{\omega }$
, there is
$0<n<{\omega }$
, there is
![]() $\varepsilon _{1}(n)$
such that if
$\varepsilon _{1}(n)$
such that if
![]() $x,y\in S$
are such that
$x,y\in S$
are such that
![]() $\vert x-y\vert <4M/(n(N)+1)$
, then
$\vert x-y\vert <4M/(n(N)+1)$
, then
![]() $\vert f(x)-f(y)\vert <\varepsilon _{1}(n(N))$
and
$\vert f(x)-f(y)\vert <\varepsilon _{1}(n(N))$
and
![]() $\varepsilon _{1}(n)$
goes to
$\varepsilon _{1}(n)$
goes to
![]() $0$
when n goes to infinity. Then for all
$0$
when n goes to infinity. Then for all
![]() $N<{\omega }$
such that
$N<{\omega }$
such that
![]() $n(N)>0$
, we can find
$n(N)>0$
, we can find
![]() $f_{N}\in C(S)$
such that
$f_{N}\in C(S)$
such that
![]() $\Vert f-f_{N}\Vert _{\infty }<\varepsilon _{1}(n(N))$
,
$\Vert f-f_{N}\Vert _{\infty }<\varepsilon _{1}(n(N))$
,
![]() $\vert f_{N}(x)\vert \le 1$
for all
$\vert f_{N}(x)\vert \le 1$
for all
![]() $x\in S$
and
$x\in S$
and
![]() $f_{N}\restriction (B^{n(N)}_{ij}-R^{n(N)}_{\varepsilon (N)})$
is constant for all
$f_{N}\restriction (B^{n(N)}_{ij}-R^{n(N)}_{\varepsilon (N)})$
is constant for all
![]() $i,j<2^{n+2}$
(here
$i,j<2^{n+2}$
(here
![]() $\varepsilon (N)$
is the one from Definition 5.16, not
$\varepsilon (N)$
is the one from Definition 5.16, not
![]() $\varepsilon _{1}(n(N))$
). Let
$\varepsilon _{1}(n(N))$
). Let
![]() $c^{N}_{ij}$
be the constant value. Now we notice that
$c^{N}_{ij}$
be the constant value. Now we notice that
![]() $\theta (f_{N})$
goes to
$\theta (f_{N})$
goes to
![]() $\theta (f)$
when
$\theta (f)$
when
![]() $n(N)$
goes to infinity and also
$n(N)$
goes to infinity and also
![]() $\langle [F^u(f_{N})]_{\infty }|[u(\theta )]_{0}\rangle $
goes to
$\langle [F^u(f_{N})]_{\infty }|[u(\theta )]_{0}\rangle $
goes to
![]() $\langle [F^u(f)]_{\infty }|[u(\theta )]_{0}\rangle $
when
$\langle [F^u(f)]_{\infty }|[u(\theta )]_{0}\rangle $
when
![]() $n(N)$
goes to infinity by the proof of Lemma 5.7 (and Lemma 5.20). Thus it is enough to show the following: Let
$n(N)$
goes to infinity by the proof of Lemma 5.7 (and Lemma 5.20). Thus it is enough to show the following: Let
![]() $\varepsilon ^{*}>0$
and
$\varepsilon ^{*}>0$
and
![]() $N<{\omega }$
be such that
$N<{\omega }$
be such that
![]() $n(N)>0$
, and
$n(N)>0$
, and
![]() $K/n(N)<\varepsilon ^{*}$
where
$K/n(N)<\varepsilon ^{*}$
where
![]() $K>0$
is a natural number such that
$K>0$
is a natural number such that
![]() $\vert \theta (f)\vert \le K\Vert f\Vert ^\sigma _{\infty }$
. Then
$\vert \theta (f)\vert \le K\Vert f\Vert ^\sigma _{\infty }$
. Then
We write
![]() $n=n(N)$
,
$n=n(N)$
,
![]() $\varepsilon =\varepsilon (N)$
,
$\varepsilon =\varepsilon (N)$
,
![]() $\delta =\delta (N)$
etc.
$\delta =\delta (N)$
etc.
Now for all
![]() $i,j<2^{n+2}$
, there is a
$i,j<2^{n+2}$
, there is a
![]() $B^{n}_{ij}$
-function
$B^{n}_{ij}$
-function
![]() $f_{ij}$
such that for all
$f_{ij}$
such that for all
![]() $x\in B^{n}_{i,j}-R^{n}_{\varepsilon }$
,
$x\in B^{n}_{i,j}-R^{n}_{\varepsilon }$
,
![]() $f_{ij}(x)=f_{N}(x)=c^{N}_{ij}$
. Let
$f_{ij}(x)=f_{N}(x)=c^{N}_{ij}$
. Let
![]() $f_{2}=\sum _{i,j<2^{n+2}}f_{ij}$
. Then (as
$f_{2}=\sum _{i,j<2^{n+2}}f_{ij}$
. Then (as
![]() $\delta <\varepsilon ^*$
) it is enough to show that
$\delta <\varepsilon ^*$
) it is enough to show that
For this it is enough to show that for all
![]() $i,j <2^{n+2}$
,
$i,j <2^{n+2}$
,
where by
![]() $F_{N}(f_{N}\restriction B^{n}_{i,j})$
we mean
$F_{N}(f_{N}\restriction B^{n}_{i,j})$
we mean
![]() $\sum _{\lambda _{N}(k)\in B^{n}_{ij}}\xi _{N}(k)f_{N}(\lambda _{N}(k))u_{N}(k)$
.
$\sum _{\lambda _{N}(k)\in B^{n}_{ij}}\xi _{N}(k)f_{N}(\lambda _{N}(k))u_{N}(k)$
.
Now if
![]() $\mu (B^{n}_{ij})=0$
, then
$\mu (B^{n}_{ij})=0$
, then
![]() $B^{n}_{ij}\cap \sigma (A)=\emptyset $
by the definition of
$B^{n}_{ij}\cap \sigma (A)=\emptyset $
by the definition of
![]() $\tilde {\sigma }(A)$
and Lemma 3.12 and thus
$\tilde {\sigma }(A)$
and Lemma 3.12 and thus
![]() $\theta (f_{ij})=0$
since
$\theta (f_{ij})=0$
since
![]() $f_{ij}$
is
$f_{ij}$
is
![]() $\sim _{\infty }$
-equivalent with the constant zero function. Clearly then also
$\sim _{\infty }$
-equivalent with the constant zero function. Clearly then also
![]() $\langle F_{N}(f_{N}\restriction B^{n}_{i,j})|u_{N}(\theta )\rangle =0$
. Thus from now on we may assume that
$\langle F_{N}(f_{N}\restriction B^{n}_{i,j})|u_{N}(\theta )\rangle =0$
. Thus from now on we may assume that
![]() $\mu (B^{n}_{ij})>0$
.
$\mu (B^{n}_{ij})>0$
.
But then it is enough to show that
since
-
(*) if
 $\mu (B^{n}_{ij})>0$
, then
$\mu (B^{n}_{ij})>0$
, then  $$ \begin{align*}(\sum_{\lambda_{N}(k)\in B^{n}_{ij}\cap R^{n}_{\varepsilon}}\vert\xi_{N}(k)\vert^{2})/\mu_{N}(B^{n}_{ij})\le\delta/\delta'\le 1/(2^{3(n+2)}).\end{align*} $$
$$ \begin{align*}(\sum_{\lambda_{N}(k)\in B^{n}_{ij}\cap R^{n}_{\varepsilon}}\vert\xi_{N}(k)\vert^{2})/\mu_{N}(B^{n}_{ij})\le\delta/\delta'\le 1/(2^{3(n+2)}).\end{align*} $$
But then it is enough to show that
Since
![]() $\theta (B^{n}_{ij}, c^{N}_{ij})=\overline {c^{N}_{ij}}\theta (B^{n}_{ij},1)=\overline {f_{ij}(x)}\theta (B^{n}_{ij},1)$
for any
$\theta (B^{n}_{ij}, c^{N}_{ij})=\overline {c^{N}_{ij}}\theta (B^{n}_{ij},1)=\overline {f_{ij}(x)}\theta (B^{n}_{ij},1)$
for any
![]() $x\in B^{n}_{ij}-R^{n}_{\varepsilon }$
, using
$x\in B^{n}_{ij}-R^{n}_{\varepsilon }$
, using
![]() $(*)$
above, this is easy.
$(*)$
above, this is easy.
Remark 5.22. The set of all generalized distributions form a vector space, we call it GDIS, under
![]() $(\theta +\theta ')(x)=\theta (x)+\theta '(x)$
and
$(\theta +\theta ')(x)=\theta (x)+\theta '(x)$
and
![]() $q\theta (x)=\theta (\overline q x)$
. Let V be a subspace of this vector space of countable dimension and let
$q\theta (x)=\theta (\overline q x)$
. Let V be a subspace of this vector space of countable dimension and let
![]() $\theta _{i}$
,
$\theta _{i}$
,
![]() $i<{\omega }$
, be a basis of this subspace. Then one can do the construction for all these generalized distributions simultaneously: One can choose the reals
$i<{\omega }$
, be a basis of this subspace. Then one can do the construction for all these generalized distributions simultaneously: One can choose the reals
![]() $r^{n}_{j}$
so that the lines
$r^{n}_{j}$
so that the lines
![]() $I_{r^{n}_{j}}$
and
$I_{r^{n}_{j}}$
and
![]() $J_{r^{n}_{j}}$
are very good for every
$J_{r^{n}_{j}}$
are very good for every
![]() $\theta _{i}$
and then one can find a pair
$\theta _{i}$
and then one can find a pair
![]() $(n,\varepsilon )$
so that it is
$(n,\varepsilon )$
so that it is
![]() $\theta _{i}$
-good for every
$\theta _{i}$
-good for every
![]() $\theta _{i}$
and in fact a bit more: Although we don’t get one W set for all the
$\theta _{i}$
and in fact a bit more: Although we don’t get one W set for all the
![]() $\theta _i$
, we can handle finitely many at a time. In Definition 5.16(ii)(a), one can require that for all
$\theta _i$
, we can handle finitely many at a time. In Definition 5.16(ii)(a), one can require that for all
![]() $R^{n}_{\varepsilon }$
-functions f and
$R^{n}_{\varepsilon }$
-functions f and
![]() $i<n$
,
$i<n$
,
![]() $\vert \theta _{i}(f)\vert <\delta /n^{2}$
(see the remark immediately after the definition). Then for all
$\vert \theta _{i}(f)\vert <\delta /n^{2}$
(see the remark immediately after the definition). Then for all
![]() $\theta \in V$
, one defines
$\theta \in V$
, one defines
![]() $W(\theta ,n,\varepsilon )$
to be the set of all
$W(\theta ,n,\varepsilon )$
to be the set of all
![]() $N<{\omega }$
such that
$N<{\omega }$
such that
![]() $n(N)>0$
and there are
$n(N)>0$
and there are
![]() $a_{i}\in \mathbb {C}$
,
$a_{i}\in \mathbb {C}$
,
![]() $i<n(N)$
, such that
$i<n(N)$
, such that
![]() $\vert a_{i}\vert \le n(N)$
and
$\vert a_{i}\vert \le n(N)$
and
![]() $\theta =\sum _{i<n(N)}a_{i}\theta _{i}$
. It is easy to see that by using these n and
$\theta =\sum _{i<n(N)}a_{i}\theta _{i}$
. It is easy to see that by using these n and
![]() $\varepsilon $
,
$\varepsilon $
,
![]() $\theta \mapsto u(\theta )$
is an embedding of V to
$\theta \mapsto u(\theta )$
is an embedding of V to
![]() $H^{m}_{0}$
so that Theorem 5.21 holds.
$H^{m}_{0}$
so that Theorem 5.21 holds.
We can now compare our construction to a rigged Hilbert space. We have defined our distributions using
![]() $C(S)$
as test functions. However, our construction disregards what happens outside
$C(S)$
as test functions. However, our construction disregards what happens outside
![]() $\sigma (A)$
, and in practice we are looking at
$\sigma (A)$
, and in practice we are looking at
![]() $C(\sigma (A))$
, which embeds into
$C(\sigma (A))$
, which embeds into
![]() $H^m_\infty $
. The distributions then embed into
$H^m_\infty $
. The distributions then embed into
![]() $H^m_0$
, so we can dig out the rigged Hilbert space in our ultraproduct. However, the construction embedding distributions into
$H^m_0$
, so we can dig out the rigged Hilbert space in our ultraproduct. However, the construction embedding distributions into
![]() $H^m_0$
can only handle countably many distributions at a time (the way we approximate the test functions over rectangles varies with the distributions), asking for a question to be posed:
$H^m_0$
can only handle countably many distributions at a time (the way we approximate the test functions over rectangles varies with the distributions), asking for a question to be posed:
Open question 4. Can one find an embedding of all of GDIS into
![]() $H^{m}_{0}$
so that Theorem 5.21 and everything in Section 5 hold for it?
$H^{m}_{0}$
so that Theorem 5.21 and everything in Section 5 hold for it?
Another natural question that arises is how canonical the norms
![]() $\lVert {\cdot }\rVert _\infty $
and
$\lVert {\cdot }\rVert _\infty $
and
![]() $\lVert {\cdot }\rVert _0$
are, as they were constructed from the chosen cyclic vector
$\lVert {\cdot }\rVert _0$
are, as they were constructed from the chosen cyclic vector
![]() $\phi $
. However, there is no reason to believe that different cyclic vectors would generate the same ultraproduct
$\phi $
. However, there is no reason to believe that different cyclic vectors would generate the same ultraproduct
![]() $H^u$
, so different norms act on different spaces. The crucial thing is that we have shown that the vectors corresponding to distributions behave in the desired way (as distributions). Thus, e.g., computing kernels (the way we consider in the next section) in spaces arising from different cyclic vectors will give the same result.
$H^u$
, so different norms act on different spaces. The crucial thing is that we have shown that the vectors corresponding to distributions behave in the desired way (as distributions). Thus, e.g., computing kernels (the way we consider in the next section) in spaces arising from different cyclic vectors will give the same result.
6 Dirac delta functions and the Feynman propagator
We now turn to the study of the Feynman propagator. In [Reference Hirvonen and Hyttinen6] we studied the kernel vs. Feynman propagator for two simple quantum mechanical systems. To explain the terminology, let us consider a particle in (one-dimensional) space. Its state can be described by a wave function
![]() $\varphi $
in position space, where the amplitude
$\varphi $
in position space, where the amplitude
![]() $\varphi (x)$
determines the particle’s probability of being in position x. The evolution over a given time interval is described by the propagator
$\varphi (x)$
determines the particle’s probability of being in position x. The evolution over a given time interval is described by the propagator
![]() $K(x,y)$
which expresses the probability amplitude of the particle traveling form point x to point y in the given time. (Usually the time is given as a third parameter, but with a time independent evolution operator, the question of calculating the kernel can be studied over a fixed time interval.) If the system has eigenvectors
$K(x,y)$
which expresses the probability amplitude of the particle traveling form point x to point y in the given time. (Usually the time is given as a third parameter, but with a time independent evolution operator, the question of calculating the kernel can be studied over a fixed time interval.) If the system has eigenvectors
![]() $\lvert {x}\rangle $
,
$\lvert {x}\rangle $
,
![]() $\lvert {y}\rangle $
, corresponding to the positions, one can calculate the propagator as an inner product
$\lvert {y}\rangle $
, corresponding to the positions, one can calculate the propagator as an inner product
where
![]() $K^{\Delta t}$
is the time evolution operator for the given time interval. In a system without eigenvectors, the propagator is defined as the kernel of the integral representation of the time evolution operator
$K^{\Delta t}$
is the time evolution operator for the given time interval. In a system without eigenvectors, the propagator is defined as the kernel of the integral representation of the time evolution operator
In [Reference Hirvonen and Hyttinen6] we built eigenvectors for the position and momentum operator in an ultraproduct model, by taking ultraproducts of eigenvectors in finite dimensional models. We tried to use them to calculate the propagator
![]() $\langle {y}\rvert K\lvert {x}\rangle $
in two cases, that of the free particle and that of the harmonic oscillator. However, it turned out that if one calculates the propagators in the finite dimensional models, one encounters divisibility issues, and the answer one gets is either 0 or the correct value scaled by a constant, where the constant depends on the physical system being modeled, and the answer on whether the constant divides the scaled distance of x and y,
$\langle {y}\rvert K\lvert {x}\rangle $
in two cases, that of the free particle and that of the harmonic oscillator. However, it turned out that if one calculates the propagators in the finite dimensional models, one encounters divisibility issues, and the answer one gets is either 0 or the correct value scaled by a constant, where the constant depends on the physical system being modeled, and the answer on whether the constant divides the scaled distance of x and y,
![]() $\sqrt {N}(x-y)$
, where N is the dimension of the space. One might at first argue that this divisibility problem should disappear with large enough N (the method is only used for rational x and y, and our filter picks out highly divisible Ns), but the situation is not that straightforward. The way the eigenvectors are built in the ultraproduct, we get for each position x continuum many eigenvectors orthogonal to each other, as one can choose different sequences of eigenvectors, whose eigenvalues converge to x. And in such a sequence one cannot guarantee divisibility along the way. Thus, instead of using the propagators in the finite dimensional structures directly, we ended up using them to calculate the kernel instead: we computed averages of propagator values over small areas, and only in the ultraproduct looked at the limit as these areas approached zero.
$\sqrt {N}(x-y)$
, where N is the dimension of the space. One might at first argue that this divisibility problem should disappear with large enough N (the method is only used for rational x and y, and our filter picks out highly divisible Ns), but the situation is not that straightforward. The way the eigenvectors are built in the ultraproduct, we get for each position x continuum many eigenvectors orthogonal to each other, as one can choose different sequences of eigenvectors, whose eigenvalues converge to x. And in such a sequence one cannot guarantee divisibility along the way. Thus, instead of using the propagators in the finite dimensional structures directly, we ended up using them to calculate the kernel instead: we computed averages of propagator values over small areas, and only in the ultraproduct looked at the limit as these areas approached zero.
In this section we present a way of defining Dirac deltas so that one can calculate the kernel as a propagator. Being able to find Dirac deltas is one of the main motivations for working in our general ultraproduct and looking at different norms instead of just working with
![]() $H^m_2$
. However, the way we define the Dirac deltas from distributions, has built into it the same averaging idea from [Reference Hirvonen and Hyttinen6] (Sections 3.2 and 3.3) that we described above. An easier way of calculating the kernel is a kind of midway between the approaches: We can find approximations of the Dirac deltas already in
$H^m_2$
. However, the way we define the Dirac deltas from distributions, has built into it the same averaging idea from [Reference Hirvonen and Hyttinen6] (Sections 3.2 and 3.3) that we described above. An easier way of calculating the kernel is a kind of midway between the approaches: We can find approximations of the Dirac deltas already in
![]() $H^m_2$
, and if the kernel exists and is continuous, it can be calculated as a limit of inner products taken in the finite dimensional models. We start by presenting this method.
$H^m_2$
, and if the kernel exists and is continuous, it can be calculated as a limit of inner products taken in the finite dimensional models. We start by presenting this method.
So suppose B is an operator in H. Let
![]() $G^{-r}:H\rightarrow L_{2}(\sigma (A),\mu \restriction \sigma (A))$
be the isometric isomorphism determined by the following: for all
$G^{-r}:H\rightarrow L_{2}(\sigma (A),\mu \restriction \sigma (A))$
be the isometric isomorphism determined by the following: for all
![]() $f\in C(S)$
,
$f\in C(S)$
,
![]() $G^{-r}(G(f))=f\restriction \sigma (A)$
. Let
$G^{-r}(G(f))=f\restriction \sigma (A)$
. Let
![]() $G^{r}$
be the inverse of
$G^{r}$
be the inverse of
![]() $G^{-r}$
and
$G^{-r}$
and
![]() $B_{D}=G^{-r}BG^{r}$
. We suppose that B is such that there is a continuous function
$B_{D}=G^{-r}BG^{r}$
. We suppose that B is such that there is a continuous function
![]() $K(x,y):\sigma (A)^{2}\rightarrow \mathbb {C}$
such that for all polynomials
$K(x,y):\sigma (A)^{2}\rightarrow \mathbb {C}$
such that for all polynomials
![]() $P\in \mathbb {C} [X,Y]$
, there is a continuous
$P\in \mathbb {C} [X,Y]$
, there is a continuous
![]() $g\in B_{D}(f_{P})$
such that for all
$g\in B_{D}(f_{P})$
such that for all
![]() ${y\in \sigma (A)}$
,
${y\in \sigma (A)}$
,
![]() $g(y)=\int _{\sigma (A)}K(x,y)(f_{P}\restriction \sigma (A))(x))dx$
. We will write
$g(y)=\int _{\sigma (A)}K(x,y)(f_{P}\restriction \sigma (A))(x))dx$
. We will write
![]() $B_{D}(f_{P})$
also for this continuous g. Notice that from these assumptions it follows, e.g., that B is bounded and that for all
$B_{D}(f_{P})$
also for this continuous g. Notice that from these assumptions it follows, e.g., that B is bounded and that for all
![]() $f\in D(S)$
,
$f\in D(S)$
,
![]() $B_{D}(f)\in C(S)$
.
$B_{D}(f)\in C(S)$
.
As justification for our assumptions, note that if we are going to calculate the kernel of B in the ‘spectral basis of A’, it makes sense to assume that B has one. As for continuity, the motivation of these questions comes from physics where most phenomena are modeled by continuous functions, especially when approximating methods are concerned. For example, the propagator of the free particle and the harmonic oscillator are continuous for nontrivial cases (meaning the time difference and angular frequency are nonzero). In the trivial case, the time evolution operator is just the identical operator, which does not have a continuous kernel. Here, if one would try to calculate with our Dirac deltas, one would get a function
![]() $K(x,y)$
that is 0 when
$K(x,y)$
that is 0 when
![]() $x\neq y$
and not defined (infinite) for
$x\neq y$
and not defined (infinite) for
![]() $x=y$
. As our method only produces functions
$x=y$
. As our method only produces functions
![]() $\sigma (A)^2\to \mathbb {C}$
as kernels, this is the closest we can get to the solution one sees in physics text books, but it is not a proper kernel representation, and we have not pursued this direction. Thus we are assuming that K is not only measurable but even continuous.
$\sigma (A)^2\to \mathbb {C}$
as kernels, this is the closest we can get to the solution one sees in physics text books, but it is not a proper kernel representation, and we have not pursued this direction. Thus we are assuming that K is not only measurable but even continuous.
However, we want to work in
![]() $L_{2}(S,\mu )$
in place of
$L_{2}(S,\mu )$
in place of
![]() $L_{2}(\sigma (A),\mu \restriction \sigma (A))$
. For this we choose a continuation of K to
$L_{2}(\sigma (A),\mu \restriction \sigma (A))$
. For this we choose a continuation of K to
![]() $S^{2}$
and we call this continuation also K and we call
$S^{2}$
and we call this continuation also K and we call
![]() $G^{-1}BG$
also
$G^{-1}BG$
also
![]() $B_{D}$
and we notice that for all polynomials
$B_{D}$
and we notice that for all polynomials
![]() $P\in \mathbb {C} [X,Y]$
,
$P\in \mathbb {C} [X,Y]$
,
![]() $g(y)=\int _{S}K(x,y)f_{P}(x)dx$
belongs to
$g(y)=\int _{S}K(x,y)f_{P}(x)dx$
belongs to
![]() $B_{D}(f_{P})$
, since
$B_{D}(f_{P})$
, since
 $$ \begin{align*}\int_{\sigma (A)}K(x,y)(f_{P}(x)\restriction\sigma (A))dx=(\int_{S}K(x,y)f_{P}(x)dx)\restriction\sigma (A)\end{align*} $$
$$ \begin{align*}\int_{\sigma (A)}K(x,y)(f_{P}(x)\restriction\sigma (A))dx=(\int_{S}K(x,y)f_{P}(x)dx)\restriction\sigma (A)\end{align*} $$
as one can easily see and again call also this function
![]() $B_{D}(f_{P})$
. If we want to do the calculations in the finite dimensional spaces
$B_{D}(f_{P})$
. If we want to do the calculations in the finite dimensional spaces
![]() $H_{N}$
we need to find suitable operators
$H_{N}$
we need to find suitable operators
![]() $B_{N}$
on these spaces.
$B_{N}$
on these spaces.
Although we later will end up working with generalized distributions
![]() $\theta $
(and then need to look in
$\theta $
(and then need to look in
![]() $H^u$
with various norms), the approximating kernel method we are adopting from [Reference Hirvonen and Hyttinen6, Section 3] works also inside
$H^u$
with various norms), the approximating kernel method we are adopting from [Reference Hirvonen and Hyttinen6, Section 3] works also inside
![]() $H^{m}$
(in fact in
$H^{m}$
(in fact in
![]() $H^{Im}$
as we will see) which appears a more natural place to work, and so we start by looking at the
$H^{Im}$
as we will see) which appears a more natural place to work, and so we start by looking at the
![]() $L_{2}$
-norm. When we move to Dirac deltas we will need stronger assumptions. Our first assumption on the operators
$L_{2}$
-norm. When we move to Dirac deltas we will need stronger assumptions. Our first assumption on the operators
![]() $B_{N}$
is the following:
$B_{N}$
is the following:
-
(C1) There is a natural number
 $K_{D}$
such that for all
$K_{D}$
such that for all
 $N<{\omega }$
and
$N<{\omega }$
and
 $v\in H_{N}$
,
$v\in H_{N}$
,  $$ \begin{align*}\Vert B_{N}(v)\Vert <K_{D}\Vert v\Vert .\end{align*} $$
$$ \begin{align*}\Vert B_{N}(v)\Vert <K_{D}\Vert v\Vert .\end{align*} $$
Notice that from this (C1) it follows that the ultraproduct
![]() $B^{u}$
of the operators
$B^{u}$
of the operators
![]() $B_{N}$
gives a well-defined bounded operator on all of
$B_{N}$
gives a well-defined bounded operator on all of
![]() $H^{m}$
. We call this operator
$H^{m}$
. We call this operator
![]() $B^{m}$
.
$B^{m}$
.
The second assumption is the obvious requirement that if we write
![]() $B^{Im}$
for the restriction of
$B^{Im}$
for the restriction of
![]() $B^{m}$
to
$B^{m}$
to
![]() $H^{Im}$
, then
$H^{Im}$
, then
-
(C2)
 $B^{Im}=G^{m}B(G^{m})^{-1}$
(=
$B^{Im}=G^{m}B(G^{m})^{-1}$
(=
 $F^mB_{D}(F^m)^{-1}$
).
$F^mB_{D}(F^m)^{-1}$
).
So how can one find the operators
![]() $B_{N}$
? First of all, in fact, they need not be linear functions as long as the ultraproduct of them is nice enough. However in practice one probably wants them to be operators. Examples of finding these can be found in [Reference Hirvonen and Hyttinen6], although the situation there is not exactly the same as here. In the case of the free particle [Reference Hirvonen and Hyttinen6, Section 3.1], B had a definition in terms of an operator C for which we already had operators
$B_{N}$
? First of all, in fact, they need not be linear functions as long as the ultraproduct of them is nice enough. However in practice one probably wants them to be operators. Examples of finding these can be found in [Reference Hirvonen and Hyttinen6], although the situation there is not exactly the same as here. In the case of the free particle [Reference Hirvonen and Hyttinen6, Section 3.1], B had a definition in terms of an operator C for which we already had operators
![]() $C_{N}$
and we used this definition in the spaces
$C_{N}$
and we used this definition in the spaces
![]() $H_{N}$
to get operators
$H_{N}$
to get operators
![]() $B_{N}$
. In the case of the harmonic oscillator we could have done essentially the same. However it turned out that with this definition
$B_{N}$
. In the case of the harmonic oscillator we could have done essentially the same. However it turned out that with this definition
![]() $K(x,y)$
was very difficult to calculate. Thus we used another method that gave completely different operators
$K(x,y)$
was very difficult to calculate. Thus we used another method that gave completely different operators
![]() $B_{N}$
but whose ultraproduct was the same (upto
$B_{N}$
but whose ultraproduct was the same (upto
![]() $\sim _{2}$
) in the places that mattered (see [Reference Hirvonen and Hyttinen6, Section 3.3]).
$\sim _{2}$
) in the places that mattered (see [Reference Hirvonen and Hyttinen6, Section 3.3]).
In the next lemma we show that the operators
![]() $B_{N}$
always exist. The proof is existential, i.e., the method used there cannot be used to find the operators in practice, unless one already knows the value of the kernel. Also, as pointed out above, the best way of choosing the operators may be such that it gives operators that are very different from those chosen in the proof of the lemma. In [Reference Hirvonen and Hyttinen6, Section 3.3] there is an example of using operators, that are wrong in almost all the finite dimensional models, and whose ultraproduct thus is wrong also in the full metric ultraproduct, but for which the restriction to the image of the original model (corresponding to
$B_{N}$
always exist. The proof is existential, i.e., the method used there cannot be used to find the operators in practice, unless one already knows the value of the kernel. Also, as pointed out above, the best way of choosing the operators may be such that it gives operators that are very different from those chosen in the proof of the lemma. In [Reference Hirvonen and Hyttinen6, Section 3.3] there is an example of using operators, that are wrong in almost all the finite dimensional models, and whose ultraproduct thus is wrong also in the full metric ultraproduct, but for which the restriction to the image of the original model (corresponding to
![]() $H^{Im}$
here) is correct.
$H^{Im}$
here) is correct.
The operators defined in the proof will be useful later, as it will turn out they are even better behaved than required here.
Lemma 6.1. There are operators
![]() $B_{N}$
in the spaces
$B_{N}$
in the spaces
![]() $H_{N}$
such that they satisfy
$H_{N}$
such that they satisfy
![]() $($
C1
$($
C1
![]() $)$
and
$)$
and
![]() $($
C2
$($
C2
![]() $)$
above.
$)$
above.
Proof. We define
![]() $B_{N}$
as follows. Let
$B_{N}$
as follows. Let
![]() $v=\sum _{n=0}^{D_{N}-1}a_{n}u_{N}(n)\in H_{N}$
. Then we let
$v=\sum _{n=0}^{D_{N}-1}a_{n}u_{N}(n)\in H_{N}$
. Then we let
 $$ \begin{align*}B_{N}(v)=\sum_{n=0}^{D_{N}-1}\sum_{k=0}^{D_{N}-1}\xi_{N}(k)\xi_{N}(n)a_{k}K(\lambda_{N}(k),\lambda_{N}(n))u_{N}(n).\end{align*} $$
$$ \begin{align*}B_{N}(v)=\sum_{n=0}^{D_{N}-1}\sum_{k=0}^{D_{N}-1}\xi_{N}(k)\xi_{N}(n)a_{k}K(\lambda_{N}(k),\lambda_{N}(n))u_{N}(n).\end{align*} $$
Clearly
![]() $B_{N}$
is a linear function.
$B_{N}$
is a linear function.
Let
![]() $K_{D}$
be a natural number greater than any of the absolute values of the values of the function K. Then
$K_{D}$
be a natural number greater than any of the absolute values of the values of the function K. Then
 $$ \begin{align*}\Vert B_{N}(v)\Vert^2_{2}\le\sum_{n=0}^{D_{N}-1}\sum_{k=0}^{D_{N}-1}\xi_{N}(k)^{2}\xi_{N}(n)^{2}\vert a_{k}K(\lambda_{N}(k),\lambda_{N}(n))\vert^{2}\le\end{align*} $$
$$ \begin{align*}\Vert B_{N}(v)\Vert^2_{2}\le\sum_{n=0}^{D_{N}-1}\sum_{k=0}^{D_{N}-1}\xi_{N}(k)^{2}\xi_{N}(n)^{2}\vert a_{k}K(\lambda_{N}(k),\lambda_{N}(n))\vert^{2}\le\end{align*} $$
 $$ \begin{align*}\le K_{D}^{2}\Vert v\Vert^2_{2}\sum_{n=0}^{D_{N}-1}\xi_{N}(n)^{2}=K_{D}^{2}\Vert v\Vert^2_{2}.\end{align*} $$
$$ \begin{align*}\le K_{D}^{2}\Vert v\Vert^2_{2}\sum_{n=0}^{D_{N}-1}\xi_{N}(n)^{2}=K_{D}^{2}\Vert v\Vert^2_{2}.\end{align*} $$
So (C1) holds.
From the definition of the functions
![]() $B_{N}$
and the uniform continuity of the functions K and
$B_{N}$
and the uniform continuity of the functions K and
![]() $f_{P}$
, it is easy to see that for all
$f_{P}$
, it is easy to see that for all
![]() $P\in \mathbb {C} [X,Y]$
,
$P\in \mathbb {C} [X,Y]$
,
![]() $[(B_{N}(F_{N}(f_{P})))_{N<{\omega }}]_{2}=[(F_{N}(B_{D}(f_{P})))_{N<{\omega }}]_{2}$
. But then (C2) follows (since the vectors
$[(B_{N}(F_{N}(f_{P})))_{N<{\omega }}]_{2}=[(F_{N}(B_{D}(f_{P})))_{N<{\omega }}]_{2}$
. But then (C2) follows (since the vectors
![]() $[(F_{N}(f_{P}))_{N<{\omega }}]_{2}$
,
$[(F_{N}(f_{P}))_{N<{\omega }}]_{2}$
,
![]() $P\in \mathbb {C} [X,Y]$
, are dense in
$P\in \mathbb {C} [X,Y]$
, are dense in
![]() $H^{Im}$
).
$H^{Im}$
).
From now on we will write
![]() $\tilde {B}_{N}$
for the operators
$\tilde {B}_{N}$
for the operators
![]() $B_{N}$
from the proof of Lemma 6.1
$B_{N}$
from the proof of Lemma 6.1
![]() $\tilde {B}^{u}$
for their ultraproduct and
$\tilde {B}^{u}$
for their ultraproduct and
![]() $\tilde {B}^{m}$
for their metric ultraproduct.
$\tilde {B}^{m}$
for their metric ultraproduct.
Now we want to calculate
![]() $K({\alpha } ,{\beta } )$
for
$K({\alpha } ,{\beta } )$
for
![]() ${\alpha } ,{\beta }\in \sigma (A)$
from operators
${\alpha } ,{\beta }\in \sigma (A)$
from operators
![]() $B_{N}$
,
$B_{N}$
,
![]() $N<{\omega }$
, that satisfy (C1) and (C2). We start by looking at the method used in [Reference Hirvonen and Hyttinen6], namely computing the kernel as a limit of approximate kernels (or propagators, as computed in the finite dimensional spaces). The Dirac delta method will be developed as a consequence. Now we choose numbers
$N<{\omega }$
, that satisfy (C1) and (C2). We start by looking at the method used in [Reference Hirvonen and Hyttinen6], namely computing the kernel as a limit of approximate kernels (or propagators, as computed in the finite dimensional spaces). The Dirac delta method will be developed as a consequence. Now we choose numbers
![]() $r^{n}_{i}$
for
$r^{n}_{i}$
for
![]() $n<{\omega }$
and
$n<{\omega }$
and
![]() $i<2^{n+2}+1$
(and lines
$i<2^{n+2}+1$
(and lines
![]() $I_{r^{n}_{i}}$
and
$I_{r^{n}_{i}}$
and
![]() $J_{r^{n}_{i}}$
) as in Section 5 so that Definition 5.13 holds when (ii) is replaced by
$J_{r^{n}_{i}}$
) as in Section 5 so that Definition 5.13 holds when (ii) is replaced by
(ii)’ for all
![]() $m<{\omega }$
, neither
$m<{\omega }$
, neither
![]() ${\alpha }$
nor
${\alpha }$
nor
![]() ${\beta }$
is in any line
${\beta }$
is in any line
![]() $I_{r^{m}_{i}}$
or
$I_{r^{m}_{i}}$
or
![]() $J_{r^{m}_{i}}$
,
$J_{r^{m}_{i}}$
,
![]() $i<2^{m+2}+1$
, and for all
$i<2^{m+2}+1$
, and for all
![]() $\delta>0$
there is
$\delta>0$
there is
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $\mu ^{n}(R^{m}_{\varepsilon })<\delta $
, where
$\mu ^{n}(R^{m}_{\varepsilon })<\delta $
, where
![]() $R^{m}_{\varepsilon }$
is as in Section 5.
$R^{m}_{\varepsilon }$
is as in Section 5.
For all
![]() $p<{\omega }$
, we let
$p<{\omega }$
, we let
![]() $B^p_{\alpha }$
be the
$B^p_{\alpha }$
be the
![]() $B^p_{ij}$
containing
$B^p_{ij}$
containing
![]() ${\alpha }$
, and let
${\alpha }$
, and let
![]() $u^{p}_{{\alpha }}=(u^{p}_{{\alpha }}(N))_{N<{\omega }}/{\mathcal {U}}$
, where
$u^{p}_{{\alpha }}=(u^{p}_{{\alpha }}(N))_{N<{\omega }}/{\mathcal {U}}$
, where
 $$ \begin{align*}u^{p}_{{\alpha}}(N)=\sum_{\lambda_{N}(k)\in B^{p}_{{\alpha}}}(\xi_{N}(k)/\mu_{N}(B^{p}_{{\alpha}}))u_{N}(k)\end{align*} $$
$$ \begin{align*}u^{p}_{{\alpha}}(N)=\sum_{\lambda_{N}(k)\in B^{p}_{{\alpha}}}(\xi_{N}(k)/\mu_{N}(B^{p}_{{\alpha}}))u_{N}(k)\end{align*} $$
and similarly for
![]() ${\beta }$
in place of
${\beta }$
in place of
![]() ${\alpha }$
. Notice that
${\alpha }$
. Notice that
![]() $\Vert u^{p}_{{\alpha }}\Vert ^2_{2}=1/\mu (B^{p}_{{\alpha }})$
and thus
$\Vert u^{p}_{{\alpha }}\Vert ^2_{2}=1/\mu (B^{p}_{{\alpha }})$
and thus
![]() $[u^{p}_{{\alpha }}]_{2}\in H^{m}_{2}$
whenever
$[u^{p}_{{\alpha }}]_{2}\in H^{m}_{2}$
whenever
![]() ${\alpha }\in \sigma (A)$
.
${\alpha }\in \sigma (A)$
.
Theorem 6.2. When
![]() ${\alpha },{\beta }\in \sigma (A)$
,
${\alpha },{\beta }\in \sigma (A)$
,
![]() $K({\alpha } ,{\beta } )=\lim _{p\rightarrow \infty }\langle [u^{p}_{{\beta }}]_{2}\vert B^{m}([u^{p}_{{\alpha }}]_{2})\rangle $
.
$K({\alpha } ,{\beta } )=\lim _{p\rightarrow \infty }\langle [u^{p}_{{\beta }}]_{2}\vert B^{m}([u^{p}_{{\alpha }}]_{2})\rangle $
.
Proof. We write
![]() $\chi _{B^{n}_{ij}}$
for the characteristic function of
$\chi _{B^{n}_{ij}}$
for the characteristic function of
![]() $B^{n}_{ij}$
and
$B^{n}_{ij}$
and
![]() $\chi ^{\prime }_{B^{n}_{ij}}$
for the function
$\chi ^{\prime }_{B^{n}_{ij}}$
for the function
![]() $\chi ^{\prime }_{B^{n}_{ij}}(x)=\chi _{B^{n}_{ij}}(x)/\mu (B^{n}_{ij})$
. Since we can approximate
$\chi ^{\prime }_{B^{n}_{ij}}(x)=\chi _{B^{n}_{ij}}(x)/\mu (B^{n}_{ij})$
. Since we can approximate
![]() $\chi ^{\prime }_{B^{p}_{{\alpha }}}$
by polynomials in the
$\chi ^{\prime }_{B^{p}_{{\alpha }}}$
by polynomials in the
![]() $L_{2}$
-norm, it is easy to see that
$L_{2}$
-norm, it is easy to see that
Notice that from this it follows that
![]() $[u^{p}_{{\alpha }}]_{2}\in H^{Im}$
. Now using this, the approximations again, (C1), (C2) and the proof of Lemma 6.1,
$[u^{p}_{{\alpha }}]_{2}\in H^{Im}$
. Now using this, the approximations again, (C1), (C2) and the proof of Lemma 6.1,
We are left with an easy calculation:
 $$ \begin{align*} \langle u^{p}_{{\beta}}(N)\vert &\tilde{B}_{N}(u^{p}_{{\alpha}}(N))\rangle=\\ =\langle \sum_{\lambda_{N}(k)\in B^{p}_{{\beta}}}(\xi_{N}(k)/\mu_{N}(B^{p}_{{\beta}}))u_{N}(k)\vert& \\ \sum_{n=0}^{D_{N}-1}\sum_{\lambda_{N}(l)\in B^{p}_{{\alpha}}} K(\lambda_{N}(l),\lambda_{N}(n))& \xi_{N}(l)^{2}\xi_{N}(n)\mu_{N}(B^{p}_{{\alpha}})^{-1}u_{N}(n)\rangle =\\ =\sum_{\lambda_{N}(k)\in B^{p}_{{\beta}}}\sum_{\lambda_{N}(l)\in B^{p}_{{\alpha}}} K(\lambda_{N}(l),\lambda_{N}(k))&\xi_{N}(l)^{2}\xi_{N}(k)^{2}(\mu_{N}(B^{p}_{{\alpha}})\mu_{N}(B^{p}_{{\beta}}))^{-1}. \end{align*} $$
$$ \begin{align*} \langle u^{p}_{{\beta}}(N)\vert &\tilde{B}_{N}(u^{p}_{{\alpha}}(N))\rangle=\\ =\langle \sum_{\lambda_{N}(k)\in B^{p}_{{\beta}}}(\xi_{N}(k)/\mu_{N}(B^{p}_{{\beta}}))u_{N}(k)\vert& \\ \sum_{n=0}^{D_{N}-1}\sum_{\lambda_{N}(l)\in B^{p}_{{\alpha}}} K(\lambda_{N}(l),\lambda_{N}(n))& \xi_{N}(l)^{2}\xi_{N}(n)\mu_{N}(B^{p}_{{\alpha}})^{-1}u_{N}(n)\rangle =\\ =\sum_{\lambda_{N}(k)\in B^{p}_{{\beta}}}\sum_{\lambda_{N}(l)\in B^{p}_{{\alpha}}} K(\lambda_{N}(l),\lambda_{N}(k))&\xi_{N}(l)^{2}\xi_{N}(k)^{2}(\mu_{N}(B^{p}_{{\alpha}})\mu_{N}(B^{p}_{{\beta}}))^{-1}. \end{align*} $$
Now keeping in mind that K is a continuous function, when p is large enough, this is roughly
 $$ \begin{align*}\sum_{\lambda_{N}(k)\in B^{p}_{{\beta}}}\sum_{\lambda_{N}(l)\in B^{p}_{{\alpha}}}K({\alpha},{\beta})\xi_{N}(l)^{2}\xi_{N}(k)^{2}(\mu_{N}(B^{p}_{{\alpha}})\mu_{N}(B^{p}_{{\beta}}))^{-1}=K({\alpha} ,{\beta}),\end{align*} $$
$$ \begin{align*}\sum_{\lambda_{N}(k)\in B^{p}_{{\beta}}}\sum_{\lambda_{N}(l)\in B^{p}_{{\alpha}}}K({\alpha},{\beta})\xi_{N}(l)^{2}\xi_{N}(k)^{2}(\mu_{N}(B^{p}_{{\alpha}})\mu_{N}(B^{p}_{{\beta}}))^{-1}=K({\alpha} ,{\beta}),\end{align*} $$
since the absolute value of the error is at most the maximum of
for
![]() $\lambda _{N}(k)\in B^{p}_{{\beta }}$
and
$\lambda _{N}(k)\in B^{p}_{{\beta }}$
and
![]() $\lambda _{N}(l)\in B^{p}_{{\alpha }}$
as a straightforward calculation shows.
$\lambda _{N}(l)\in B^{p}_{{\alpha }}$
as a straightforward calculation shows.
Now we can turn to Dirac deltas. We let
![]() $\theta _{{\alpha }}$
be the generalized distribution such that
$\theta _{{\alpha }}$
be the generalized distribution such that
![]() $\theta _{{\alpha }}(f)=f({\alpha } )$
for all
$\theta _{{\alpha }}(f)=f({\alpha } )$
for all
![]() $f\in C(S)$
and
$f\in C(S)$
and
![]() $\theta _{{\beta }}$
is defined similarly. Now it is easy to see that for all
$\theta _{{\beta }}$
is defined similarly. Now it is easy to see that for all
![]() $n<{\omega }$
and
$n<{\omega }$
and
![]() $i<2^{n+2}+1$
, the
$i<2^{n+2}+1$
, the
![]() $I_{r^{n}_{i}}$
and
$I_{r^{n}_{i}}$
and
![]() $J_{r^{n}_{i}}$
chosen above for Theorem 6.2 are very good for both
$J_{r^{n}_{i}}$
chosen above for Theorem 6.2 are very good for both
![]() $\theta _{{\alpha }}$
and
$\theta _{{\alpha }}$
and
![]() $\theta _{{\beta }}$
, i.e., all the requirements of Definition 5.13 are satisfied. It follows that we can find a pair
$\theta _{{\beta }}$
, i.e., all the requirements of Definition 5.13 are satisfied. It follows that we can find a pair
![]() $(n,\varepsilon )$
so that it is
$(n,\varepsilon )$
so that it is
![]() $\theta _{{\alpha }}$
-good and
$\theta _{{\alpha }}$
-good and
![]() $\theta _{{\beta }}$
-good (see the end of Section 5). We will need one more requirement for the pair
$\theta _{{\beta }}$
-good (see the end of Section 5). We will need one more requirement for the pair
![]() $(n,\varepsilon )$
. We will return to this once we have looked at the requirements for the operators
$(n,\varepsilon )$
. We will return to this once we have looked at the requirements for the operators
![]() $B_{N}$
,
$B_{N}$
,
![]() $N<{\omega }$
.
$N<{\omega }$
.
Again, recall that the pair
![]() $(n,\varepsilon )$
determines the function u (see Definition 5.19) and (independent of the last requirement) notice that
$(n,\varepsilon )$
determines the function u (see Definition 5.19) and (independent of the last requirement) notice that
![]() $\Vert u(\theta _{{\alpha }})\Vert ^{u}_{0}=1$
and thus
$\Vert u(\theta _{{\alpha }})\Vert ^{u}_{0}=1$
and thus
![]() $[u(\theta _{{\alpha }})]_{0}\in H^{m}_{0}$
(and similarly for
$[u(\theta _{{\alpha }})]_{0}\in H^{m}_{0}$
(and similarly for
![]() ${\beta }$
). However
${\beta }$
). However
![]() $\Vert u(\theta _{{\alpha }})\Vert _{\infty }$
is infinite (unless
$\Vert u(\theta _{{\alpha }})\Vert _{\infty }$
is infinite (unless
![]() $\alpha $
is an actual eigenvalue), as we can see below:
$\alpha $
is an actual eigenvalue), as we can see below:
 $$ \begin{align*} u_{N}(\theta_{\alpha} )&=\sum_{\mu (B^{n(N)}_{ij})\ne 0}\sum_{\lambda_{N}(k)\in B^{n(N)}_{ij}}(\xi_{N}(k)\theta_{\alpha} (B^{n(N)}_{ij},1)/\mu_{N}(B^{n(N)}_{ij}))u_{N}(k)\\ &=\left\{\begin{array}{ll} \sum_{\lambda_{N}(k)\in B^{n(N)}_{{\alpha}}}(\xi_{N}(k)/\mu_{N}(B^{n(N)}_{{\alpha}}))u_{N}(k), &\text{if }\mu(B^{n(N)}_{\alpha})\ne 0,\\ 0,&\text{otherwise.}\end{array}\right. \end{align*} $$
$$ \begin{align*} u_{N}(\theta_{\alpha} )&=\sum_{\mu (B^{n(N)}_{ij})\ne 0}\sum_{\lambda_{N}(k)\in B^{n(N)}_{ij}}(\xi_{N}(k)\theta_{\alpha} (B^{n(N)}_{ij},1)/\mu_{N}(B^{n(N)}_{ij}))u_{N}(k)\\ &=\left\{\begin{array}{ll} \sum_{\lambda_{N}(k)\in B^{n(N)}_{{\alpha}}}(\xi_{N}(k)/\mu_{N}(B^{n(N)}_{{\alpha}}))u_{N}(k), &\text{if }\mu(B^{n(N)}_{\alpha})\ne 0,\\ 0,&\text{otherwise.}\end{array}\right. \end{align*} $$
Now (assuming
![]() $\mu (B^{n(N)}_{\alpha })\ne 0$
, which by Lemma 3.12 happens in an
$\mu (B^{n(N)}_{\alpha })\ne 0$
, which by Lemma 3.12 happens in an
![]() ${\mathcal {U}}$
-large set as long as
${\mathcal {U}}$
-large set as long as
![]() ${\alpha }\in \sigma (A)$
, which is the case relevant for Dirac deltas),
${\alpha }\in \sigma (A)$
, which is the case relevant for Dirac deltas),
But, unless
![]() ${\alpha }$
is an eigenvalue,
${\alpha }$
is an eigenvalue,
![]() $\mu _N(B^{n(N)}_{\alpha })$
will become arbitrary small, making
$\mu _N(B^{n(N)}_{\alpha })$
will become arbitrary small, making
![]() $\Vert u(\theta _{{\alpha }})\Vert ^\varepsilon _{\infty }$
infinite (see Definition 5.5), and this causes problems, as the inner product in the Feynman propagator may not be well-defined. So we need to modify the assumptions (C1) and (C2).
$\Vert u(\theta _{{\alpha }})\Vert ^\varepsilon _{\infty }$
infinite (see Definition 5.5), and this causes problems, as the inner product in the Feynman propagator may not be well-defined. So we need to modify the assumptions (C1) and (C2).
We let
![]() $H^{\infty }_{\infty }$
be
$H^{\infty }_{\infty }$
be
![]() $H^{u}/\sim _{\infty }$
. This is a natural space to consider Dirac deltas, as it is large enough to allow for ‘infinite’ objects, and on the other hand has a very delicate equivalence class structure, avoiding the risk of putting into the same equivalence class objects that behave differently in our calculations. Now our first assumption requires that the ultraproduct of the operators
$H^{u}/\sim _{\infty }$
. This is a natural space to consider Dirac deltas, as it is large enough to allow for ‘infinite’ objects, and on the other hand has a very delicate equivalence class structure, avoiding the risk of putting into the same equivalence class objects that behave differently in our calculations. Now our first assumption requires that the ultraproduct of the operators
![]() $B_{N}$
gives a well-defined operator on
$B_{N}$
gives a well-defined operator on
![]() $H^{\infty }_{\infty }$
. We will call the operator
$H^{\infty }_{\infty }$
. We will call the operator
![]() $B^{\infty }$
:
$B^{\infty }$
:
-
(C1)’ There is a natural number
 $K_{D}$
such that for all
$K_{D}$
such that for all
 $N<{\omega }$
and
$N<{\omega }$
and
 $v\in H_{N}$
,
$v\in H_{N}$
,  $$ \begin{align*}\Vert B_{N}(v)\Vert^{S}_{\infty} <K_{D}\Vert v\Vert^{S}_{\infty}.\end{align*} $$
$$ \begin{align*}\Vert B_{N}(v)\Vert^{S}_{\infty} <K_{D}\Vert v\Vert^{S}_{\infty}.\end{align*} $$
Our second assumption ties the values of
![]() $B_{N}$
to values of
$B_{N}$
to values of
![]() $B_{D}$
in the sense of
$B_{D}$
in the sense of
![]() $\Vert \cdot \Vert _{\infty }$
. Here we use basically the simple functions since our definition of the function u is based on them. However, notice that instead of simple functions we could use polynomials here as well as in Section 5, but this would make the definition of u much more complicated.
$\Vert \cdot \Vert _{\infty }$
. Here we use basically the simple functions since our definition of the function u is based on them. However, notice that instead of simple functions we could use polynomials here as well as in Section 5, but this would make the definition of u much more complicated.
We write
![]() $F^u(\chi ^{\prime }_{B^{n}_{ij}})$
for
$F^u(\chi ^{\prime }_{B^{n}_{ij}})$
for
![]() $(F_{N}(\chi ^{\prime }_{B^{n}_{ij}}))_{N<{\omega }}/{\mathcal {U}}$
where
$(F_{N}(\chi ^{\prime }_{B^{n}_{ij}}))_{N<{\omega }}/{\mathcal {U}}$
where
 $$ \begin{align*}F_{N}(\chi^{\prime}_{B^{n}_{ij}})=\sum_{n=0}^{D_{N}-1}\xi_{N}(n)\chi^{\prime}_{B^{n}_{ij}}(\lambda_{N}(n))u_N(n).\end{align*} $$
$$ \begin{align*}F_{N}(\chi^{\prime}_{B^{n}_{ij}})=\sum_{n=0}^{D_{N}-1}\xi_{N}(n)\chi^{\prime}_{B^{n}_{ij}}(\lambda_{N}(n))u_N(n).\end{align*} $$
We also write
![]() $B_{D}(\chi ^{\prime }_{B^{n}_{ij}})$
for the function
$B_{D}(\chi ^{\prime }_{B^{n}_{ij}})$
for the function
![]() $g(y)=\int _{S}K(x,y)\chi ^{\prime }_{B^{n}_{ij}}(x)dx$
. Then (C2) implies
$g(y)=\int _{S}K(x,y)\chi ^{\prime }_{B^{n}_{ij}}(x)dx$
. Then (C2) implies
And now following this we assume:
-
(C2)’ For all
 $B^{n}_{ij}$
,
$B^{n}_{ij}$
,  $$ \begin{align*}B^{\infty}([F^u(\chi^{\prime}_{B^{n}_{ij}})]_{\infty})=[F^u(B_{D}(\chi^{\prime}_{B^{n}_{ij}}))]_{\infty}.\end{align*} $$
$$ \begin{align*}B^{\infty}([F^u(\chi^{\prime}_{B^{n}_{ij}})]_{\infty})=[F^u(B_{D}(\chi^{\prime}_{B^{n}_{ij}}))]_{\infty}.\end{align*} $$
We recall that if
![]() $\Vert (v_{N})_{N<{\omega }}/{\mathcal {U}}\Vert _{\infty }<\infty $
and for all
$\Vert (v_{N})_{N<{\omega }}/{\mathcal {U}}\Vert _{\infty }<\infty $
and for all
![]() $N<{\omega }$
,
$N<{\omega }$
,
![]() $v_{N}=\sum _{n=0}^{D_{N}-1}a^{N}_{n}u_{N}(n)$
, then there are
$v_{N}=\sum _{n=0}^{D_{N}-1}a^{N}_{n}u_{N}(n)$
, then there are
![]() $W\in {\mathcal {U}}$
and a natural number p such that for all
$W\in {\mathcal {U}}$
and a natural number p such that for all
![]() $N\in W$
and
$N\in W$
and
![]() $n<D_{N}$
,
$n<D_{N}$
,
![]() $\vert \xi _{N}(n)^{-1}a^{N}_{n}\vert <p$
. However,
$\vert \xi _{N}(n)^{-1}a^{N}_{n}\vert <p$
. However,
![]() $B^{\infty }$
images of Dirac’s deltas don’t necessarily have this property. The values may not have a uniform bound for all N. For suitably chosen
$B^{\infty }$
images of Dirac’s deltas don’t necessarily have this property. The values may not have a uniform bound for all N. For suitably chosen
![]() $H^m_0$
-vectors one could still get finite values from the pairing function, but this would be kind of accidental, like getting arbitrary values for a product like
$H^m_0$
-vectors one could still get finite values from the pairing function, but this would be kind of accidental, like getting arbitrary values for a product like
![]() $0\cdot \infty $
. We suspect one could build a situation where (C1)’, (C2)’, and (*) below holds, and
$0\cdot \infty $
. We suspect one could build a situation where (C1)’, (C2)’, and (*) below holds, and
![]() $u(\theta _{{\alpha }})$
and
$u(\theta _{{\alpha }})$
and
![]() $u(\theta _{{\beta }})$
give Feynman’s propagator the value
$u(\theta _{{\beta }})$
give Feynman’s propagator the value
![]() $K({\alpha } ,{\beta } )$
, but for this kind of wrong reason. So we introduce one more requirement for the operators
$K({\alpha } ,{\beta } )$
, but for this kind of wrong reason. So we introduce one more requirement for the operators
![]() $B_{N}$
(it is a bit unnecessarily strong, but we are just making a point).
$B_{N}$
(it is a bit unnecessarily strong, but we are just making a point).
-
(C3)’ There is a natural number p such that for all
 $n<{\omega }$
,
$n<{\omega }$
,
 $i,j<2^{n+2}+1$
and
$i,j<2^{n+2}+1$
and
 $N<{\omega }$
,
$N<{\omega }$
,
 $\Vert B_{N}(u^{n}_{ij}(N))\Vert ^{S}_{\infty }<p$
, where when
$\Vert B_{N}(u^{n}_{ij}(N))\Vert ^{S}_{\infty }<p$
, where when $$ \begin{align*}u^{n}_{ij}(N)=\sum_{\lambda_{N}(k)\in B^{n}_{ij}}(\xi_{N}(k)/\mu_{N}(B^{n}_{ij}))u_{N}(k),\end{align*} $$
$$ \begin{align*}u^{n}_{ij}(N)=\sum_{\lambda_{N}(k)\in B^{n}_{ij}}(\xi_{N}(k)/\mu_{N}(B^{n}_{ij}))u_{N}(k),\end{align*} $$
 $\mu _N(B^n_{ij})\neq 0$
, and 0 otherwise.
$\mu _N(B^n_{ij})\neq 0$
, and 0 otherwise.
Lemma 6.3. The operators
![]() $\tilde {B}_{N}$
,
$\tilde {B}_{N}$
,
![]() $N<{\omega }$
, satisfy
$N<{\omega }$
, satisfy
![]() $($
C1
$($
C1
![]() $)$
’,
$)$
’,
![]() $($
C2
$($
C2
![]() $)$
’, and
$)$
’, and
![]() $($
C3
$($
C3
![]() $)$
’.
$)$
’.
Proof. (C1)’ and (C2)’ can be proved essentially as in the proof of Lemma 6.1 and (C3)’ is a straightforward calculation.
Let us return to the choice of the pair
![]() $(n,\varepsilon )$
and thus to the choice of u. We choose it so that in addition to what we have already said, the following holds: There are
$(n,\varepsilon )$
and thus to the choice of u. We choose it so that in addition to what we have already said, the following holds: There are
![]() $W(\theta _{{\alpha }},n,\varepsilon )$
and
$W(\theta _{{\alpha }},n,\varepsilon )$
and
![]() $W(\theta _{{\beta }},n,\varepsilon )$
that witness that
$W(\theta _{{\beta }},n,\varepsilon )$
that witness that
![]() $(n,\varepsilon )$
is both
$(n,\varepsilon )$
is both
![]() $\theta _{{\alpha }}$
-good and
$\theta _{{\alpha }}$
-good and
![]() $\theta _{{\beta }}$
-good and
$\theta _{{\beta }}$
-good and
-
(*) if
 $N\in W(\theta _{{\alpha }},n,\varepsilon )\cap W(\theta _{{\beta }},n,\varepsilon )$
and
$N\in W(\theta _{{\alpha }},n,\varepsilon )\cap W(\theta _{{\beta }},n,\varepsilon )$
and
 $p=n(N)>0$
, then
$p=n(N)>0$
, then  $$ \begin{align*}\vert \langle u^{p}_{{\beta}}(N)\vert B_{N}(u^{p}_{{\alpha}}(N))\rangle-\langle u^{p}_{{\beta}}\vert B^{u}(u^{p}_{{\alpha}})\rangle\vert <p^{-1}.\end{align*} $$
$$ \begin{align*}\vert \langle u^{p}_{{\beta}}(N)\vert B_{N}(u^{p}_{{\alpha}}(N))\rangle-\langle u^{p}_{{\beta}}\vert B^{u}(u^{p}_{{\alpha}})\rangle\vert <p^{-1}.\end{align*} $$
It is easy to see that this is possible.
Proposition 6.4. Suppose
![]() $($
C1
$($
C1
![]() $)$
’,
$)$
’,
![]() $($
C2
$($
C2
![]() $)$
’ and
$)$
’ and
![]() $($
C3
$($
C3
![]() $)$
’ hold, and
$)$
’ hold, and
![]() ${\alpha },{\beta }\in \sigma (A)$
. Then
${\alpha },{\beta }\in \sigma (A)$
. Then
Proof. Notice that if
![]() $p=n(N)>0$
, then
$p=n(N)>0$
, then
![]() $F_N(\chi _{B^p_{\alpha }}\mu _N(B^p_{\alpha })^{-1})=u^{p}_{{\alpha }}(N)=u_{N}(\theta _{{\alpha }})$
and
$F_N(\chi _{B^p_{\alpha }}\mu _N(B^p_{\alpha })^{-1})=u^{p}_{{\alpha }}(N)=u_{N}(\theta _{{\alpha }})$
and
![]() $(F_N(\chi _{B^p_{\alpha }}\mu _N(B^p_{\alpha })^{-1}))_{N<{\omega }}/{\mathcal {U}}\in [F^u(\chi ^{\prime }_{B^p_{\alpha }})]_\infty $
. and so from (C3)’ it follows that
$(F_N(\chi _{B^p_{\alpha }}\mu _N(B^p_{\alpha })^{-1}))_{N<{\omega }}/{\mathcal {U}}\in [F^u(\chi ^{\prime }_{B^p_{\alpha }})]_\infty $
. and so from (C3)’ it follows that
![]() $B^{\infty }[u(\theta _{{\alpha }})]_{\infty }\in H^{m}_{\infty }$
and thus by Lemma 5.7,
$B^{\infty }[u(\theta _{{\alpha }})]_{\infty }\in H^{m}_{\infty }$
and thus by Lemma 5.7,
i.e., it is well-defined. By (C2)’ and Lemma 6.3,
![]() $B^{\infty }([u^{n}_{{\alpha }}]_{\infty })=[\tilde {B}^{u}(u^{n}_{{\alpha }})]_{\infty }$
, for all
$B^{\infty }([u^{n}_{{\alpha }}]_{\infty })=[\tilde {B}^{u}(u^{n}_{{\alpha }})]_{\infty }$
, for all
![]() $n<{\omega }$
. But then the claim follows from (the proof of) Theorem 6.2 and (*) above.
$n<{\omega }$
. But then the claim follows from (the proof of) Theorem 6.2 and (*) above.
Remark 6.5. Let Z be the set of all r for which there is
![]() $\delta>0$
such that either for all
$\delta>0$
such that either for all
![]() $\varepsilon>0$
$\varepsilon>0$
![]() $\mu ^{n}(I_{r}^{\varepsilon })\ge \delta $
or for all
$\mu ^{n}(I_{r}^{\varepsilon })\ge \delta $
or for all
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $\mu ^{n}(J^{\varepsilon }_{r})\ge \delta $
. In Section 3 we saw that Z is countable. Let
$\mu ^{n}(J^{\varepsilon }_{r})\ge \delta $
. In Section 3 we saw that Z is countable. Let
![]() $Y=\cup _{r\in Z}(I_{r}\cup J_{r})$
. Then as in the end of Section 5, we can see that for any countable
$Y=\cup _{r\in Z}(I_{r}\cup J_{r})$
. Then as in the end of Section 5, we can see that for any countable
![]() $X\subseteq \sigma (A)-Y$
, we can choose a pair
$X\subseteq \sigma (A)-Y$
, we can choose a pair
![]() $(n,\varepsilon )$
so that it is
$(n,\varepsilon )$
so that it is
![]() $\theta _{{\alpha }}$
-good for all
$\theta _{{\alpha }}$
-good for all
![]() ${\alpha }\in X$
, i.e., Theorem 5.21 holds, (*) above holds for every pair
${\alpha }\in X$
, i.e., Theorem 5.21 holds, (*) above holds for every pair
![]() $({\alpha },{\beta } )\in X^{2}$
and in addition u gives an embedding of the vector space generated by the Dirac deltas
$({\alpha },{\beta } )\in X^{2}$
and in addition u gives an embedding of the vector space generated by the Dirac deltas
![]() $\theta _{{\alpha }}$
,
$\theta _{{\alpha }}$
,
![]() ${\alpha }\in X$
, into
${\alpha }\in X$
, into
![]() $H^{m}_{0}$
. So we can make everything in Sections 4 and 5 work for all
$H^{m}_{0}$
. So we can make everything in Sections 4 and 5 work for all
![]() $\theta _{{\alpha }}$
,
$\theta _{{\alpha }}$
,
![]() ${\alpha }\in X$
, simultaneously. If X is dense in
${\alpha }\in X$
, simultaneously. If X is dense in
![]() $\sigma (A)$
, one expects that this is enough for most arguments in the contexts where the essential phenomena are modeled by continuous functions.
$\sigma (A)$
, one expects that this is enough for most arguments in the contexts where the essential phenomena are modeled by continuous functions.
7 The non-cyclic case
We finally look at the case where the operator doesn’t have a cyclic vector. Then H can be decomposed into a countable direct sum
![]() $\bigoplus _{i<\omega } H_i$
of subspaces
$\bigoplus _{i<\omega } H_i$
of subspaces
![]() $H_i$
, invariant under A and with a cyclic vector
$H_i$
, invariant under A and with a cyclic vector
![]() $v_i$
. By the construction for the cyclic case, each
$v_i$
. By the construction for the cyclic case, each
![]() $H_i$
is isomorphic to a space
$H_i$
is isomorphic to a space
![]() $L_2(S,\mu _i)$
, where every
$L_2(S,\mu _i)$
, where every
![]() $\mu _i$
is a Borel measure with
$\mu _i$
is a Borel measure with
![]() $\mu _i(S)=1$
.
$\mu _i(S)=1$
.
Now, to combine these, let
 $$ \begin{align*}\mu=\sum_{i=0}^{\infty} 2^{-i-1}\mu_i. \end{align*} $$
$$ \begin{align*}\mu=\sum_{i=0}^{\infty} 2^{-i-1}\mu_i. \end{align*} $$
Then
![]() $\mu $
is a finite Borel measure, and every
$\mu $
is a finite Borel measure, and every
![]() $\mu _i$
is absolutely continuous with respect to
$\mu _i$
is absolutely continuous with respect to
![]() $\mu $
. Thus by the Radon–Nikodym theorem there are Borel functions
$\mu $
. Thus by the Radon–Nikodym theorem there are Borel functions
![]() $f_i$
such that for all Borel sets
$f_i$
such that for all Borel sets
![]() $A\subseteq S$
$A\subseteq S$
This means that each
![]() $L_2(S,\mu _i)$
can be isometrically embedded into
$L_2(S,\mu _i)$
can be isometrically embedded into
![]() $L_2(S,\mu )$
by the mapping generated by
$L_2(S,\mu )$
by the mapping generated by
Now if we wish to combine the direct sum of these into an
![]() $L_2$
space over a finite measure space, we can turn to the Bochner spaces, which are function spaces of vector valued functions (see, e.g., [Reference Hytönen, van Neerven, Veraar and Weis7]). We can recognize the space
$L_2$
space over a finite measure space, we can turn to the Bochner spaces, which are function spaces of vector valued functions (see, e.g., [Reference Hytönen, van Neerven, Veraar and Weis7]). We can recognize the space
![]() $\oplus _{i<\omega }L_2(S,\mu )$
as a Bochner-
$\oplus _{i<\omega }L_2(S,\mu )$
as a Bochner-
![]() $\ell _2$
-space with values in the space
$\ell _2$
-space with values in the space
![]() $L_2(S,\mu ;\mathbb {C})$
, i.e.,
$L_2(S,\mu ;\mathbb {C})$
, i.e.,
![]() $\ell _2(L_2(S,\mu ;\mathbb {C}))$
. By [Reference Hytönen, van Neerven, Veraar and Weis7, Corollary 1.2.23]
$\ell _2(L_2(S,\mu ;\mathbb {C}))$
. By [Reference Hytönen, van Neerven, Veraar and Weis7, Corollary 1.2.23]
![]() $\ell _2(L_2(S,\mu ;\mathbb {C}))\cong L_2(S,\mu ;\ell _2(\mathbb {C}))$
, where the latter is the vector valued
$\ell _2(L_2(S,\mu ;\mathbb {C}))\cong L_2(S,\mu ;\ell _2(\mathbb {C}))$
, where the latter is the vector valued
![]() $L_2$
-space over S with values in
$L_2$
-space over S with values in
![]() $\ell _2(\mathbb {C})$
. Our sum space
$\ell _2(\mathbb {C})$
. Our sum space
![]() $\oplus _iH_i$
can now be isometrically embedded into this space by combining the isometric isomorphisms
$\oplus _iH_i$
can now be isometrically embedded into this space by combining the isometric isomorphisms
![]() $H_i\cong L_2(S,\mu _i)$
obtained from our previous theory, the embeddings
$H_i\cong L_2(S,\mu _i)$
obtained from our previous theory, the embeddings
![]() $L_2(S,\mu _i)\hookrightarrow L_2(S,\mu )$
, and finally the isomorphism
$L_2(S,\mu _i)\hookrightarrow L_2(S,\mu )$
, and finally the isomorphism
![]() $\ell _2(L_2(S,\mu ;\mathbb {C}))\cong L_2(S,\mu ;\ell _2(\mathbb {C}))$
.
$\ell _2(L_2(S,\mu ;\mathbb {C}))\cong L_2(S,\mu ;\ell _2(\mathbb {C}))$
.
If we denote the image under this embedding by
![]() $H'$
, we can as before find a copy of
$H'$
, we can as before find a copy of
![]() $H'$
within a suitable ultraproduct of finite-dimensional spaces: If we denote by
$H'$
within a suitable ultraproduct of finite-dimensional spaces: If we denote by
![]() $H^i_N$
the finite dimensional subspaces of
$H^i_N$
the finite dimensional subspaces of
![]() $H_i$
constructed as before, we can construct spaces
$H_i$
constructed as before, we can construct spaces
and build the ultraproduct model from these. A canonical modification of the embedding
![]() $G^m$
gives an embedding of
$G^m$
gives an embedding of
![]() $\oplus _{i<\omega }H_i$
(and thus of
$\oplus _{i<\omega }H_i$
(and thus of
![]() $H'$
) into the metric ultraproduct and allows us to use finite dimensional approximations. It is worth noting that this does not give an embedding of all of
$H'$
) into the metric ultraproduct and allows us to use finite dimensional approximations. It is worth noting that this does not give an embedding of all of
![]() $L_2(S,\mu ;\ell _2(\mathbb {C}))$
into the metric ultraproduct.
$L_2(S,\mu ;\ell _2(\mathbb {C}))$
into the metric ultraproduct.
Now, although we can find a spectral decomposition of our space in an ultraproduct of finite-dimensional spaces, we don’t see that this would give a general approach to kernels. If the operator B behaves differently in the different spaces
![]() $H_i$
, one doesn’t get a common complex-valued kernel that could be used for the vectors of the Bochner space. And if the
$H_i$
, one doesn’t get a common complex-valued kernel that could be used for the vectors of the Bochner space. And if the
![]() $H_i$
aren’t invariant under B, one cannot treat these spaces separately, either.
$H_i$
aren’t invariant under B, one cannot treat these spaces separately, either.