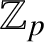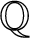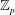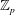2 results
ON FINE SELMER GROUPS AND SIGNED SELMER GROUPS OF ELLIPTIC MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 419-430
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Growth of Fine Selmer Groups in Infinite Towers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 13 March 2020, pp. 921-936
- Print publication:
- December 2020
-
- Article
- Export citation