Allocation of a redundant component in a system in order to optimize, in some sense, the lifetime of the system is an important problem in reliability theory, having practical applications. Consider a series system consisting of two components (say C1 and C2), having independent random lifetimes X1 and X2, and suppose a component C having random lifetime X (independent of X1 and X2) is available for active redundancy with one of the components. Let U1 = min(max(X1, X), X2) and U2 = min(X1, max(X2, X)), so that U1 (U2) denote the lifetime of a system obtained by allocating C to C1 (C2). We consider the criterion where C1 is preferred to C2 for redundancy allocation if 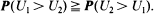 . Here we investigate the problem of allocating C to C1 or C2, with respect to the above criterion. We also consider the standby redundancy for series and parallel systems with respect to the above criterion. The problem of allocating an active redundant component in order that the resulting system has the smallest failure rate function is also considered and it is observed that unlike stochastic optimization, here the lifetime distribution of the redundant component also plays a role, making the problem of even active redundancy allocation more complex.
. Here we investigate the problem of allocating C to C1 or C2, with respect to the above criterion. We also consider the standby redundancy for series and parallel systems with respect to the above criterion. The problem of allocating an active redundant component in order that the resulting system has the smallest failure rate function is also considered and it is observed that unlike stochastic optimization, here the lifetime distribution of the redundant component also plays a role, making the problem of even active redundancy allocation more complex.

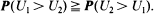 . Here we investigate the problem of allocating
. Here we investigate the problem of allocating 