Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Singh, Harshinder
and
Singh, R. S.
1997.
On allocation of spares at component level versus system level.
Journal of Applied Probability,
Vol. 34,
Issue. 01,
p.
283.
Prasad, V.R.
Way Kuo
and
Oh Kim, K.M.
1999.
Optimal allocation of s-identical, multi-functional spares in a series system.
IEEE Transactions on Reliability,
Vol. 48,
Issue. 2,
p.
118.
Mi, Jie
1999.
Optimal active redundancy allocation in k-out-of-n system.
Journal of Applied Probability,
Vol. 36,
Issue. 3,
p.
927.
Mi, Jie
1999.
Optimal active redundancy allocation in k-out-of-n system.
Journal of Applied Probability,
Vol. 36,
Issue. 03,
p.
927.
Arcones, Miguel A
Kvam, Paul H
and
Samaniego, Francisco J
2002.
Nonparametric Estimation of a Distribution Subject to a Stochastic Precedence Constraint.
Journal of the American Statistical Association,
Vol. 97,
Issue. 457,
p.
170.
Valdés, José E.
and
Zequeira, Rómulo I.
2003.
On the optimal allocation of an active redundancy in a two-component series system.
Statistics & Probability Letters,
Vol. 63,
Issue. 3,
p.
325.
Jie Mi
2003.
A unified way of comparing the reliability of coherent systems.
IEEE Transactions on Reliability,
Vol. 52,
Issue. 1,
p.
38.
Romera, R.
Valdes, J.
and
Zequeira, R.I.
2004.
Active-Redundancy Allocation in Systems.
IEEE Transactions on Reliability,
Vol. 53,
Issue. 3,
p.
313.
da Costa Bueno, Vanderlei
2005.
Minimal standby redundancy allocation in a k-out-of-n:F system of dependent components.
European Journal of Operational Research,
Vol. 165,
Issue. 3,
p.
786.
Boland, Philip J.
and
Singh, Harshinder
2006.
Advances in Distribution Theory, Order Statistics, and Inference.
p.
3.
Kokolakis, George
and
Papageorgiou, Effie
2006.
Scheduling starting times for an active redundant system with non-identical lifetimes.
Applied Mathematical Modelling,
Vol. 30,
Issue. 12,
p.
1535.
Belzunce, Félix
Ortega, Eva-María
Pellerey, Franco
and
Ruiz, José M.
2007.
On rankings and top choices in random utility models with dependent utilities.
Metrika,
Vol. 66,
Issue. 2,
p.
197.
da Costa Bueno, Vanderlei
and
Martins do Carmo, Iran
2007.
Active redundancy allocation for a k-out-of-n:F system of dependent components.
European Journal of Operational Research,
Vol. 176,
Issue. 2,
p.
1041.
Li, Xiaohu
and
Hu, Xiaoxiao
2008.
Some new stochastic comparisons for redundancy allocations in series and parallel systems.
Statistics & Probability Letters,
Vol. 78,
Issue. 18,
p.
3388.
Li, Xiaohu
Zhang, Zhengcheng
and
Wu, Yudan
2009.
Some new results involving general standby systems.
Applied Stochastic Models in Business and Industry,
Vol. 25,
Issue. 5,
p.
632.
Valdés, José E.
Arango, Gerardo
Zequeira, Romulo I.
and
Brito, Gerandy
2010.
Some stochastic comparisons in series systems with active redundancy.
Statistics & Probability Letters,
Vol. 80,
Issue. 11-12,
p.
945.
Li, Xiaohu
Yan, Rongfang
and
Hu, Xiaoxiao
2011.
On the Allocation of Redundancies in Series and Parallel Systems.
Communications in Statistics - Theory and Methods,
Vol. 40,
Issue. 6,
p.
959.
Brito, Gerandy
Zequeira, Romulo I.
and
Valdés, José E.
2011.
On the hazard rate and reversed hazard rate orderings in two-component series systems with active redundancies.
Statistics & Probability Letters,
Vol. 81,
Issue. 2,
p.
201.
Belzunce, Félix
Martínez-Puertas, Helena
and
Ruiz, José M.
2011.
On optimal allocation of redundant components for series and parallel systems of two dependent components.
Journal of Statistical Planning and Inference,
Vol. 141,
Issue. 9,
p.
3094.
Misra, Amit Kumar
and
Misra, Neeraj
2011.
A note on active redundancy allocations in -out-of- systems.
Statistics & Probability Letters,
Vol. 81,
Issue. 10,
p.
1518.
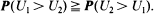 . Here we investigate the problem of allocating C to C1 or C2, with respect to the above criterion. We also consider the standby redundancy for series and parallel systems with respect to the above criterion. The problem of allocating an active redundant component in order that the resulting system has the smallest failure rate function is also considered and it is observed that unlike stochastic optimization, here the lifetime distribution of the redundant component also plays a role, making the problem of even active redundancy allocation more complex.
. Here we investigate the problem of allocating C to C1 or C2, with respect to the above criterion. We also consider the standby redundancy for series and parallel systems with respect to the above criterion. The problem of allocating an active redundant component in order that the resulting system has the smallest failure rate function is also considered and it is observed that unlike stochastic optimization, here the lifetime distribution of the redundant component also plays a role, making the problem of even active redundancy allocation more complex.