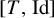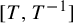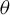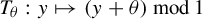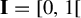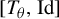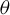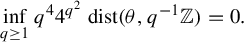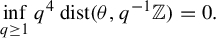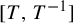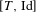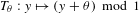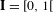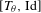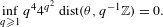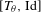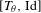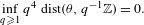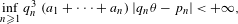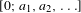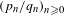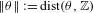Let  \unicode[STIX]{x1D703} be an irrational real number. The map
\unicode[STIX]{x1D703} be an irrational real number. The map 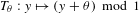 T_{\unicode[STIX]{x1D703}}:y\mapsto (y+\unicode[STIX]{x1D703})\!\hspace{0.6em}{\rm mod}\hspace{0.2em}1 from the unit interval
T_{\unicode[STIX]{x1D703}}:y\mapsto (y+\unicode[STIX]{x1D703})\!\hspace{0.6em}{\rm mod}\hspace{0.2em}1 from the unit interval 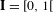 \mathbf{I}= [\!0,1\![ (endowed with the Lebesgue measure) to itself is ergodic. In a short paper [Parry, Automorphisms of the Bernoulli endomorphism and a class of skew-products. Ergod. Th. & Dynam. Sys.16 (1996), 519–529] published in 1996, Parry provided an explicit isomorphism between the measure-preserving map
\mathbf{I}= [\!0,1\![ (endowed with the Lebesgue measure) to itself is ergodic. In a short paper [Parry, Automorphisms of the Bernoulli endomorphism and a class of skew-products. Ergod. Th. & Dynam. Sys.16 (1996), 519–529] published in 1996, Parry provided an explicit isomorphism between the measure-preserving map 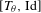 [T_{\unicode[STIX]{x1D703}},\text{Id}] and the unilateral dyadic Bernoulli shift when
[T_{\unicode[STIX]{x1D703}},\text{Id}] and the unilateral dyadic Bernoulli shift when  \unicode[STIX]{x1D703} is extremely well approximated by the rational numbers, namely, if
\unicode[STIX]{x1D703} is extremely well approximated by the rational numbers, namely, if
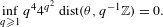 \begin{eqnarray}\inf _{q\geq 1}q^{4}4^{q^{2}}~\text{dist}(\unicode[STIX]{x1D703},q^{-1}\mathbb{Z})=0.\end{eqnarray}
\begin{eqnarray}\inf _{q\geq 1}q^{4}4^{q^{2}}~\text{dist}(\unicode[STIX]{x1D703},q^{-1}\mathbb{Z})=0.\end{eqnarray} A few years later, Hoffman and Rudolph [Uniform endomorphisms which are isomorphic to a Bernoulli shift.
Ann. of Math. (2)156 (2002), 79–101] showed that for every irrational number, the measure-preserving map
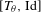 [T_{\unicode[STIX]{x1D703}},\text{Id}]
[T_{\unicode[STIX]{x1D703}},\text{Id}] is isomorphic to the unilateral dyadic Bernoulli shift. Their proof is not constructive. In the present paper, we relax notably Parry’s condition on
 \unicode[STIX]{x1D703}
\unicode[STIX]{x1D703}: the explicit map provided by Parry’s method is an isomorphism between the map
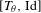 [T_{\unicode[STIX]{x1D703}},\text{Id}]
[T_{\unicode[STIX]{x1D703}},\text{Id}] and the unilateral dyadic Bernoulli shift whenever
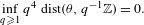 \begin{eqnarray}\inf _{q\geq 1}q^{4}~\text{dist}(\unicode[STIX]{x1D703},q^{-1}\mathbb{Z})=0.\end{eqnarray}
\begin{eqnarray}\inf _{q\geq 1}q^{4}~\text{dist}(\unicode[STIX]{x1D703},q^{-1}\mathbb{Z})=0.\end{eqnarray} This condition can be relaxed again into
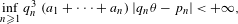 \begin{eqnarray}\inf _{n\geq 1}q_{n}^{3}~(a_{1}+\cdots +a_{n})~|q_{n}\unicode[STIX]{x1D703}-p_{n}|<+\infty ,\end{eqnarray}
\begin{eqnarray}\inf _{n\geq 1}q_{n}^{3}~(a_{1}+\cdots +a_{n})~|q_{n}\unicode[STIX]{x1D703}-p_{n}|<+\infty ,\end{eqnarray} where
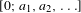 [0;a_{1},a_{2},\ldots ]
[0;a_{1},a_{2},\ldots ] is the continued fraction expansion and
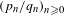 (p_{n}/q_{n})_{n\geq 0}
(p_{n}/q_{n})_{n\geq 0} the sequence of convergents of
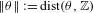 \Vert \unicode[STIX]{x1D703}\Vert :=\text{dist}(\unicode[STIX]{x1D703},\mathbb{Z})
\Vert \unicode[STIX]{x1D703}\Vert :=\text{dist}(\unicode[STIX]{x1D703},\mathbb{Z}). Whether Parry’s map is an isomorphism for every
 \unicode[STIX]{x1D703}
\unicode[STIX]{x1D703} or not is still an open question, although we expect a positive answer.