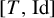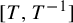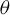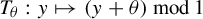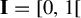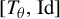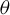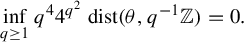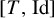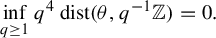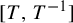1 Introduction
In this section, we present general properties of Meilijson’s skew products
![]() $[T,\mathrm {Id}]$
and
$[T,\mathrm {Id}]$
and
![]() $[T,T^{-1}]$
before focusing on the case where T is an irrational rotation.
$[T,T^{-1}]$
before focusing on the case where T is an irrational rotation.
1.1 Meilijson’s skew products
 $[T,\mathrm {Id}]$
and
$[T,\mathrm {Id}]$
and
 $[T,T^{-1}]$
$[T,T^{-1}]$
Let
![]() $X = \{0,1\}^{\mathbb {Z}_+}$
, endowed with the product sigma-field
$X = \{0,1\}^{\mathbb {Z}_+}$
, endowed with the product sigma-field
![]() $\mathcal {X}$
and the product measure
$\mathcal {X}$
and the product measure
 $$ \begin{align*}\mu := \bigotimes_{n \in \mathbb{Z}_+} (\delta_0+\delta_1)/2.\end{align*} $$
$$ \begin{align*}\mu := \bigotimes_{n \in \mathbb{Z}_+} (\delta_0+\delta_1)/2.\end{align*} $$
The shift operator
![]() $S : X \to X$
, defined by
$S : X \to X$
, defined by
preserves the measure
![]() $\mu $
.
$\mu $
.
Given any automorphism T of a probability space
![]() $(Y,\mathcal {Y},\nu )$
, one defines the map
$(Y,\mathcal {Y},\nu )$
, one defines the map
![]() $[T,\mathrm {Id}]$
from
$[T,\mathrm {Id}]$
from
![]() $X \times Y$
to itself by
$X \times Y$
to itself by
On the first component, the map
![]() $[T,\mathrm {Id}]$
simply applies the shift S. If we totally ignore the first component, the map
$[T,\mathrm {Id}]$
simply applies the shift S. If we totally ignore the first component, the map
![]() $[T,\mathrm {Id}]$
applies T or
$[T,\mathrm {Id}]$
applies T or
![]() $\mathrm {Id}$
at random on the second one. One can define
$\mathrm {Id}$
at random on the second one. One can define
![]() $[T,T^{-1}]$
with the same formula, just by replacing
$[T,T^{-1}]$
with the same formula, just by replacing
![]() $\{0,1\}^{\mathbb {Z}_+}$
with
$\{0,1\}^{\mathbb {Z}_+}$
with
![]() $\{-1,1\}^{\mathbb {Z}_+}$
.
$\{-1,1\}^{\mathbb {Z}_+}$
.
One checks that the transformations
![]() $[T,\mathrm {Id}]$
and
$[T,\mathrm {Id}]$
and
![]() $[T,T^{-1}]$
preserve the measure
$[T,T^{-1}]$
preserve the measure
![]() $\mu \otimes \nu $
and are two-to-one: if
$\mu \otimes \nu $
and are two-to-one: if
![]() $(x,y)$
is chosen randomly according to the distribution
$(x,y)$
is chosen randomly according to the distribution
![]() $\mu \otimes \nu $
, and if one knows
$\mu \otimes \nu $
, and if one knows
![]() $[T,\mathrm {Id}](x,y)$
(or
$[T,\mathrm {Id}](x,y)$
(or
![]() $[T,T^{-1}](x,y)$
), the only information missing to recover
$[T,T^{-1}](x,y)$
), the only information missing to recover
![]() $(x,y)$
is the value of
$(x,y)$
is the value of
![]() $x(0)$
, which is uniformly distributed on
$x(0)$
, which is uniformly distributed on
![]() $\{0,1\}$
and independent of
$\{0,1\}$
and independent of
![]() $[T,\mathrm {Id}](x,y)$
(of
$[T,\mathrm {Id}](x,y)$
(of
![]() $[T,T^{-1}](x,y)$
).
$[T,T^{-1}](x,y)$
).
Meilijson’s theorem [Reference Meilijson8] ensures that the natural extension of
![]() $[T\kern-0.5pt,\kern-1pt\mathrm{Id}]$
is a K-automorphism whenever T is ergodic and the natural extension of
$[T\kern-0.5pt,\kern-1pt\mathrm{Id}]$
is a K-automorphism whenever T is ergodic and the natural extension of
![]() $[T,T^{-1}]$
is a K-automorphism whenever T is totally ergodic (that is, all positive powers of T are ergodic). Actually, the ergodicity of T only is sufficient (and necessary) to guarantee that the endomorphism
$[T,T^{-1}]$
is a K-automorphism whenever T is totally ergodic (that is, all positive powers of T are ergodic). Actually, the ergodicity of T only is sufficient (and necessary) to guarantee that the endomorphism
![]() $[T,\mathrm {Id}]$
is exact, so its natural extension is a K-automorphism. And the ergodicity of
$[T,\mathrm {Id}]$
is exact, so its natural extension is a K-automorphism. And the ergodicity of
![]() $T^2$
only is sufficient (and necessary) to guarantee that the endomorphism
$T^2$
only is sufficient (and necessary) to guarantee that the endomorphism
![]() $[T,T^{-1}]$
is exact, so its natural extension is a K-automorphism. See Theorem 1 in [Reference Leuridan, Donati-Martin, Lejay and Rouault7].
$[T,T^{-1}]$
is exact, so its natural extension is a K-automorphism. See Theorem 1 in [Reference Leuridan, Donati-Martin, Lejay and Rouault7].
Hence, when T (respectively
![]() $T^2$
) is ergodic, a natural question arises: is the endomorphism
$T^2$
) is ergodic, a natural question arises: is the endomorphism
![]() $[T,\mathrm {Id}]$
(respectively,
$[T,\mathrm {Id}]$
(respectively,
![]() $[T,T^{-1}]$
) isomorphic to the Bernoulli shift S? The answer depends on the automorphism T considered.
$[T,T^{-1}]$
) isomorphic to the Bernoulli shift S? The answer depends on the automorphism T considered.
-
• An adaptation of techniques and ideas introduced by Vershik [Reference Vershik11, Reference Vershik12], Heicklen and Hoffman [Reference Heicklen and Hoffman2] shows that when T is a two-sided Bernoulli shift, and, more generally, when T has positive entropy, the endomorphism
 $[T,T^{-1}]$
cannot be Bernoulli since the standardness—a weaker property—fails. This argument can be adapted to the endomorphism
$[T,T^{-1}]$
cannot be Bernoulli since the standardness—a weaker property—fails. This argument can be adapted to the endomorphism
 $[T,\mathrm {Id}]$
. More details are given in [Reference Leuridan, Donati-Martin, Lejay and Rouault7].
$[T,\mathrm {Id}]$
. More details are given in [Reference Leuridan, Donati-Martin, Lejay and Rouault7]. -
• In 2000, Hoffman constructed in [Reference Hoffman3] a zero-entropy transformation T such that the
 $[T,\mathrm {Id}]$
endomorphism is non-standard. The proof is detailed in [Reference Leuridan, Donati-Martin, Lejay and Rouault7].
$[T,\mathrm {Id}]$
endomorphism is non-standard. The proof is detailed in [Reference Leuridan, Donati-Martin, Lejay and Rouault7]. -
• In 2002, Rudolph and Hoffman showed in [Reference Hoffman and Rudolph4] that, when T is an irrational rotation, the endomorphism
 $[T,\mathrm {Id}]$
is isomorphic to the dyadic Bernoulli shift S. Their proof is not constructive.
$[T,\mathrm {Id}]$
is isomorphic to the dyadic Bernoulli shift S. Their proof is not constructive.
Actually, non-trivial examples of explicit isomorphisms between measure-preserving maps are quite rare. Yet, an independent generating partition providing an explicit isomorphism between
![]() $[T,\mathrm {Id}]$
and the dyadic one-sided Bernoulli shift was given in 1996 by Parry in [Reference Parry9] when the rotation T is extremely well approximated by rational ones.
$[T,\mathrm {Id}]$
and the dyadic one-sided Bernoulli shift was given in 1996 by Parry in [Reference Parry9] when the rotation T is extremely well approximated by rational ones.
1.2 Parry’s partition
From now on, we fix an irrational number
![]() $\theta $
. We denote
$\theta $
. We denote
![]() ${\mathbf {I} = [0,1[}$
the unit interval,
${\mathbf {I} = [0,1[}$
the unit interval,
![]() $\mathcal {B}(\mathbf {I})$
its Borel
$\mathcal {B}(\mathbf {I})$
its Borel
![]() $\sigma $
-field,
$\sigma $
-field,
![]() $\nu $
the uniform distribution on
$\nu $
the uniform distribution on
![]() $\mathbf {I}$
and
$\mathbf {I}$
and
![]() $T_\theta : \mathbf {I} \to \mathbf {I}$
the translation of
$T_\theta : \mathbf {I} \to \mathbf {I}$
the translation of
![]() $\theta $
modulo
$\theta $
modulo
![]() $1$
. This transformation preserves the measure
$1$
. This transformation preserves the measure
![]() $\nu $
and can be viewed as an irrational rotation on the circle
$\nu $
and can be viewed as an irrational rotation on the circle
![]() $\mathbb {R}/\mathbb {Z}$
. However, we choose to work with the unit interval
$\mathbb {R}/\mathbb {Z}$
. However, we choose to work with the unit interval
![]() $\mathbf {I} = [0,1[$
to avoid ambiguity in the definition of the sub-intervals.
$\mathbf {I} = [0,1[$
to avoid ambiguity in the definition of the sub-intervals.
Since the transformation
![]() $T_\theta $
depends only on the equivalence class of
$T_\theta $
depends only on the equivalence class of
![]() $\theta $
in
$\theta $
in
![]() $\mathbb {R}/\mathbb {Z}$
, we may—and we shall—assume that
$\mathbb {R}/\mathbb {Z}$
, we may—and we shall—assume that
![]() $0<\theta <1$
. Hence, for every
$0<\theta <1$
. Hence, for every
![]() $y \in \mathbf {I}$
,
$y \in \mathbf {I}$
,
The map
![]() $T_\theta $
is bijective with inverse
$T_\theta $
is bijective with inverse
![]() $T_{1-\theta }= T_{-\theta }$
, given by
$T_{1-\theta }= T_{-\theta }$
, given by
Since
![]() $T_{1-\theta }= T_{-\theta }$
is isomorphic to
$T_{1-\theta }= T_{-\theta }$
is isomorphic to
![]() $T_\theta $
, we may—and we shall—assume that
$T_\theta $
, we may—and we shall—assume that
![]() $0<\theta <1/2$
.
$0<\theta <1/2$
.
In [Reference Parry9], Parry introduced the partition
![]() $\alpha _\theta = \{A_0^\theta ,A_1^\theta \}$
on
$\alpha _\theta = \{A_0^\theta ,A_1^\theta \}$
on
![]() $X \times \mathbf {I}$
defined by
$X \times \mathbf {I}$
defined by
Observe that, for every
![]() $(x,y) \in X \times \mathbf {I}$
,
$(x,y) \in X \times \mathbf {I}$
,
When we endow
![]() $X \times \mathbf {I}$
with the distribution
$X \times \mathbf {I}$
with the distribution
![]() $\mu \otimes \nu $
, the value of
$\mu \otimes \nu $
, the value of
![]() $x(0)$
is uniform and independent of
$x(0)$
is uniform and independent of
![]() $[T_\theta ,\mathrm {Id}](x,y) = (S(x),T_\theta ^{x_0}(y))$
. Thus,
$[T_\theta ,\mathrm {Id}](x,y) = (S(x),T_\theta ^{x_0}(y))$
. Thus,
Hence, the partition
![]() $\alpha _\theta $
is uniform and independent of
$\alpha _\theta $
is uniform and independent of
![]() $[T_\theta ,\mathrm {Id}]^{-1}(\mathcal {X} \otimes \mathcal {B}(\mathbf {I}))$
. An induction shows that the partitions
$[T_\theta ,\mathrm {Id}]^{-1}(\mathcal {X} \otimes \mathcal {B}(\mathbf {I}))$
. An induction shows that the partitions
![]() $([T_\theta ,\mathrm {Id}]^{-n}\alpha _\theta )_{n \ge 0}$
are independent.
$([T_\theta ,\mathrm {Id}]^{-n}\alpha _\theta )_{n \ge 0}$
are independent.
For every
![]() $(x,y) \in X \times \mathbf {I}$
, denote by
$(x,y) \in X \times \mathbf {I}$
, denote by
![]() $\alpha _\theta (x,y) = {\mathbf 1}_{A_1^\theta }(x,y)$
the index of the only block containing
$\alpha _\theta (x,y) = {\mathbf 1}_{A_1^\theta }(x,y)$
the index of the only block containing
![]() $(x,y)$
in the partition
$(x,y)$
in the partition
![]() $\alpha _\theta $
. By construction, the ‘
$\alpha _\theta $
. By construction, the ‘
![]() $\alpha _\theta $
-name’ map
$\alpha _\theta $
-name’ map
![]() ${\Phi _\theta : X \times \mathbf {I} \to X}$
, defined by
${\Phi _\theta : X \times \mathbf {I} \to X}$
, defined by
is also a factor map which sends the dynamical system
![]() $(X \times \mathbf {I},\mathcal {X} \otimes \mathcal {B}(\mathbf {I}),\mu \otimes \nu ,[T_\theta ,\mathrm {Id}])$
on the Bernoulli shift
$(X \times \mathbf {I},\mathcal {X} \otimes \mathcal {B}(\mathbf {I}),\mu \otimes \nu ,[T_\theta ,\mathrm {Id}])$
on the Bernoulli shift
![]() $(X,\mathcal {X},\mu ,S)$
.
$(X,\mathcal {X},\mu ,S)$
.
Under the assumption
Parry shows that, for
![]() $\mu \otimes \nu $
-almost every
$\mu \otimes \nu $
-almost every
![]() $(x,y) \in X \times \mathbf {I}$
, the knowledge of
$(x,y) \in X \times \mathbf {I}$
, the knowledge of
![]() $\Phi _\theta (x,y)$
is sufficient to recover
$\Phi _\theta (x,y)$
is sufficient to recover
![]() $(x,y)$
, so the factor map
$(x,y)$
, so the factor map
![]() $\Phi _\theta $
is an isomorphism.
$\Phi _\theta $
is an isomorphism.
In Theorem 1 of [Reference Leuridan6], we relaxed Parry’s condition into
Moreover, Theorem 10 and Lemma 14 of [Reference Leuridan6] show that we may relax this condition a bit more into
where
![]() $[0;a_1,a_2,\ldots ]$
is the continued fraction expansion of
$[0;a_1,a_2,\ldots ]$
is the continued fraction expansion of
![]() $\|\theta \|:=\mathrm {dist}(\theta ,\mathbb {Z})$
(which equals
$\|\theta \|:=\mathrm {dist}(\theta ,\mathbb {Z})$
(which equals
![]() $\theta $
when
$\theta $
when
![]() $0<\theta <1/2$
) and
$0<\theta <1/2$
) and
![]() $(p_n/q_n)_{n \ge 0}$
is the sequence of convergents.
$(p_n/q_n)_{n \ge 0}$
is the sequence of convergents.
Actually, there was a typo, namely, a wrong exponent in the statement of Theorem 2 of [Reference Leuridan6]. The sufficient condition given there was the stronger condition
so the result stated in Theorem 2 of [Reference Leuridan6] is weaker than what Theorem 10 and Lemma 14 of [Reference Leuridan6] actually prove, but it is still true.
Anyway, in the present paper, we remove (and not only relax) Parry’s assumption and prove that, for any irrational number
![]() $\theta $
, the factor map
$\theta $
, the factor map
![]() $\Phi _\theta $
is an isomorphism (see Theorem 1 further). Remember that the extra assumption
$\Phi _\theta $
is an isomorphism (see Theorem 1 further). Remember that the extra assumption
![]() $0 < \theta < 1/2$
that we make for convenience is not a true restriction.
$0 < \theta < 1/2$
that we make for convenience is not a true restriction.
1.3 Probabilistic reformulation
Since the transformation
![]() $T_\theta $
preserves the uniform measure on
$T_\theta $
preserves the uniform measure on
![]() $[0,1[$
, we can consider a stationary Markov chain
$[0,1[$
, we can consider a stationary Markov chain
![]() $((\xi _n,Y_n))_{n \in \mathbb {Z}}$
on
$((\xi _n,Y_n))_{n \in \mathbb {Z}}$
on
![]() $\{0,1\} \times [0,1[$
such that, for every
$\{0,1\} \times [0,1[$
such that, for every
![]() $n \in \mathbb {Z}$
:
$n \in \mathbb {Z}$
:
-
•
 $(\xi _n,Y_n)$
is uniform on
$(\xi _n,Y_n)$
is uniform on
 $\{0,1\} \times [0,1[$
;
$\{0,1\} \times [0,1[$
; -
•
 $\xi _{n}$
is independent of
$\xi _{n}$
is independent of
 $\mathcal {F}^{\xi ,Y}_{n-1} := \sigma ((\xi _k,Y_k)_{k \le n-1})$
; and
$\mathcal {F}^{\xi ,Y}_{n-1} := \sigma ((\xi _k,Y_k)_{k \le n-1})$
; and -
•
 $Y_{n} = T_{-\theta }^{\xi _{n}}(Y_{n-1}) = (Y_{n-1}-\xi _{n}\theta ) \,\mod \!\!\: 1$
.
$Y_{n} = T_{-\theta }^{\xi _{n}}(Y_{n-1}) = (Y_{n-1}-\xi _{n}\theta ) \,\mod \!\!\: 1$
.
For every real number r, denote by
![]() $\overline {r} = r+\mathbb {Z}$
the equivalence class of r modulo
$\overline {r} = r+\mathbb {Z}$
the equivalence class of r modulo
![]() $\mathbb {Z}$
. The process
$\mathbb {Z}$
. The process
![]() $(\overline {Y_n})_{n \in \mathbb {Z}}$
is as a random walk on
$(\overline {Y_n})_{n \in \mathbb {Z}}$
is as a random walk on
![]() $\mathbb {R}/\mathbb {Z}$
. The steps
$\mathbb {R}/\mathbb {Z}$
. The steps
![]() $(\overline {Y_n}-\overline {Y_{n-1}})_{n \in \mathbb {Z}} = (-\overline {\xi _n\theta })$
are uniformly distributed on
$(\overline {Y_n}-\overline {Y_{n-1}})_{n \in \mathbb {Z}} = (-\overline {\xi _n\theta })$
are uniformly distributed on
![]() $\{\overline {0},-\overline {\theta }\}$
. Since each random variable
$\{\overline {0},-\overline {\theta }\}$
. Since each random variable
![]() $\xi _n$
can be recovered from the knowledge of
$\xi _n$
can be recovered from the knowledge of
![]() $Y_n$
and
$Y_n$
and
![]() $Y_{n-1}$
, the natural filtration
$Y_{n-1}$
, the natural filtration
![]() $(\mathcal {F}^{\xi ,Y}_n)_{n \in \mathbb {Z}}$
of the Markov chain
$(\mathcal {F}^{\xi ,Y}_n)_{n \in \mathbb {Z}}$
of the Markov chain
![]() $((\xi _n,Y_n))_{n \in \mathbb {Z}}$
coincides with the the natural filtration
$((\xi _n,Y_n))_{n \in \mathbb {Z}}$
coincides with the the natural filtration
![]() $(\mathcal {F}^{Y}_n)_{n \in \mathbb {Z}}$
of the process
$(\mathcal {F}^{Y}_n)_{n \in \mathbb {Z}}$
of the process
![]() $(Y_n)_{n \in \mathbb {Z}}$
.
$(Y_n)_{n \in \mathbb {Z}}$
.
The Markov chain
![]() $((\xi _n,Y_n))_{n \in \mathbb {Z}}$
thus defined is closely related to the transformation
$((\xi _n,Y_n))_{n \in \mathbb {Z}}$
thus defined is closely related to the transformation
![]() $[T_\theta ,\mathrm {Id}]$
since, for every
$[T_\theta ,\mathrm {Id}]$
since, for every
![]() $n \in \mathbb {Z}$
,
$n \in \mathbb {Z}$
,
Knowing the sequence
![]() $(\xi _n)_{n \in \mathbb {Z}}$
only is not sufficient to recover the positions
$(\xi _n)_{n \in \mathbb {Z}}$
only is not sufficient to recover the positions
![]() $(Y_n)_{n \in \mathbb {Z}}$
. Indeed, one can check that
$(Y_n)_{n \in \mathbb {Z}}$
. Indeed, one can check that
![]() $Y_0$
is independent of the whole sequence
$Y_0$
is independent of the whole sequence
![]() $(\xi _n)_{n \in \mathbb {Z}}$
.
$(\xi _n)_{n \in \mathbb {Z}}$
.
Reformulating Parry’s method, we introduce the sequence
![]() $(\eta _n)_{n \in \mathbb {Z}}$
defined by
$(\eta _n)_{n \in \mathbb {Z}}$
defined by
 $$ \begin{align*} \eta_n &:= (\xi_n + {\mathbf 1}_{[\theta,1[}(Y_{n-1})) \,\mod\!\!\: 2\\ &= {\mathbf 1}_{[\xi_n = 0~;~Y_{n-1} \ge \theta]} + {\mathbf 1}_{[\xi_n = 1~;~Y_{n-1} < \theta]}. \end{align*} $$
$$ \begin{align*} \eta_n &:= (\xi_n + {\mathbf 1}_{[\theta,1[}(Y_{n-1})) \,\mod\!\!\: 2\\ &= {\mathbf 1}_{[\xi_n = 0~;~Y_{n-1} \ge \theta]} + {\mathbf 1}_{[\xi_n = 1~;~Y_{n-1} < \theta]}. \end{align*} $$
By construction,
![]() $\eta _n$
is an
$\eta _n$
is an
![]() $\mathcal {F}^{\xi ,Y}_n$
-measurable Bernoulli random variable; and
$\mathcal {F}^{\xi ,Y}_n$
-measurable Bernoulli random variable; and
![]() $\eta _n$
is uniform and independent of
$\eta _n$
is uniform and independent of
![]() $\mathcal {F}^{\xi ,Y}_{n-1}$
since
$\mathcal {F}^{\xi ,Y}_{n-1}$
since
Moreover, since
![]() $Y_{n} = T_{-\theta }^{\xi _{n}}(Y_{n-1})$
,
$Y_{n} = T_{-\theta }^{\xi _{n}}(Y_{n-1})$
,
 $$ \begin{align*} \eta_n &= {\mathbf 1}_{[\xi_n = 0~;~Y_n \ge \theta]} + {\mathbf 1}_{[\xi_n = 1~;~Y_n \ge 1-\theta]} \\ &= {\mathbf 1}_{A_1^\theta} ( (\xi_{n-k})_{k \ge 0},Y_n ) \\ &= {\mathbf 1}_{A_1^\theta} ( [T_\theta,\mathrm{Id}]^{-n} ((\xi_{-k})_{k \ge 0},Y_0) ) \text{ if } n \le 0. \end{align*} $$
$$ \begin{align*} \eta_n &= {\mathbf 1}_{[\xi_n = 0~;~Y_n \ge \theta]} + {\mathbf 1}_{[\xi_n = 1~;~Y_n \ge 1-\theta]} \\ &= {\mathbf 1}_{A_1^\theta} ( (\xi_{n-k})_{k \ge 0},Y_n ) \\ &= {\mathbf 1}_{A_1^\theta} ( [T_\theta,\mathrm{Id}]^{-n} ((\xi_{-k})_{k \ge 0},Y_0) ) \text{ if } n \le 0. \end{align*} $$
Hence, the
![]() $\alpha _\theta $
-name of
$\alpha _\theta $
-name of
![]() $((\xi _{-i})_{i \ge 0},Y_0)$
is the sequence
$((\xi _{-i})_{i \ge 0},Y_0)$
is the sequence
![]() $(\eta _{-i})_{i \ge 0}$
.
$(\eta _{-i})_{i \ge 0}$
.
Thus, proving that the partition
![]() $\alpha _\theta $
is generating is equivalent to proving that, almost surely, the random variable
$\alpha _\theta $
is generating is equivalent to proving that, almost surely, the random variable
![]() $Y_0$
is completely determined by the knowledge of
$Y_0$
is completely determined by the knowledge of
![]() $(\eta _{k})_{k \le 0}$
. By stationarity, it means that the filtration
$(\eta _{k})_{k \le 0}$
. By stationarity, it means that the filtration
![]() $(\mathcal {F}^{\xi ,Y}_n)_{n \in \mathbb {Z}y} = (\mathcal {F}^{Y}_n)_{n \in \mathbb {Z}}$
is generated by the sequence
$(\mathcal {F}^{\xi ,Y}_n)_{n \in \mathbb {Z}y} = (\mathcal {F}^{Y}_n)_{n \in \mathbb {Z}}$
is generated by the sequence
![]() $(\eta _n)_{n \in \mathbb {Z}}$
. Actually, we show that this property holds without any additional assumption on
$(\eta _n)_{n \in \mathbb {Z}}$
. Actually, we show that this property holds without any additional assumption on
![]() $\theta $
.
$\theta $
.
Theorem 1. For every
![]() $n \in \mathbb {Z}$
, the random variable
$n \in \mathbb {Z}$
, the random variable
![]() $Y_n$
can be almost surely recovered from the knowledge of
$Y_n$
can be almost surely recovered from the knowledge of
![]() $(\eta _k)_{k \le n}$
. Hence, the filtration
$(\eta _k)_{k \le n}$
. Hence, the filtration
![]() $(\mathcal {F}^{\xi ,Y}_n)_{n \in \mathbb {Z}} = (\mathcal {F}^{Y}_n)_{n \in \mathbb {Z}}$
is generated by the sequence
$(\mathcal {F}^{\xi ,Y}_n)_{n \in \mathbb {Z}} = (\mathcal {F}^{Y}_n)_{n \in \mathbb {Z}}$
is generated by the sequence
![]() $(\eta _n)_{n \in \mathbb {Z}}$
of independent uniform Bernoulli random variables. Equivalently, Parry’s partition
$(\eta _n)_{n \in \mathbb {Z}}$
of independent uniform Bernoulli random variables. Equivalently, Parry’s partition
![]() $\alpha _\theta $
is an independent generator of
$\alpha _\theta $
is an independent generator of
![]() $[T_\theta ,\mathrm {Id}]$
.
$[T_\theta ,\mathrm {Id}]$
.
We refer the reader to §4 for the similar statement about
![]() $[T_\theta ,T_\theta ^{-1}]$
.
$[T_\theta ,T_\theta ^{-1}]$
.
To explain why the sequence
![]() $(\eta _n)_{n \in \mathbb {Z}}$
gives more information than the sequence
$(\eta _n)_{n \in \mathbb {Z}}$
gives more information than the sequence
![]() $(\xi _n)_{n \in \mathbb {Z}}$
, we introduce the maps
$(\xi _n)_{n \in \mathbb {Z}}$
, we introduce the maps
![]() $f_0$
and
$f_0$
and
![]() $f_1$
from the interval
$f_1$
from the interval
![]() $\mathbf {I} = [0,1[$
to itself by
$\mathbf {I} = [0,1[$
to itself by
The union of the graphs of
![]() $f_0$
and
$f_0$
and
![]() $f_1$
is also the union of the graphs of
$f_1$
is also the union of the graphs of
![]() $\mathrm {Id}$
and
$\mathrm {Id}$
and
![]() $T_{-\theta }$
(see Figure 1). Therefore, applying at random
$T_{-\theta }$
(see Figure 1). Therefore, applying at random
![]() $f_0$
or
$f_0$
or
![]() $f_1$
has the same effect as applying at random
$f_1$
has the same effect as applying at random
![]() $\mathrm {Id}$
or
$\mathrm {Id}$
or
![]() $T_{-\theta }$
. Actually, a direct computation distinguishing four cases, where
$T_{-\theta }$
. Actually, a direct computation distinguishing four cases, where
![]() $\xi _n$
equals
$\xi _n$
equals
![]() $0$
or
$0$
or
![]() $1$
and
$1$
and
![]() $Y_{n-1} < \theta $
or
$Y_{n-1} < \theta $
or
![]() $Y_{n-1} \ge \theta $
yields
$Y_{n-1} \ge \theta $
yields
The great difference with the initial recursion relation
![]() $Y_{n} = T_{-\theta }^{\xi _{n}}(Y_{n-1})$
is that the maps
$Y_{n} = T_{-\theta }^{\xi _{n}}(Y_{n-1})$
is that the maps
![]() $f_0$
and
$f_0$
and
![]() $f_1$
are not injective and are not surjective, unlike
$f_1$
are not injective and are not surjective, unlike
![]() $T_{-\theta }^0 = \mathrm {Id}$
and
$T_{-\theta }^0 = \mathrm {Id}$
and
![]() $T_{-\theta }^1 = T_{-\theta }$
.
$T_{-\theta }^1 = T_{-\theta }$
.

Figure 1 Graphs of
![]() $f_0$
and
$f_0$
and
![]() $f_1$
.
$f_1$
.
For every
![]() $n \ge 1$
, denote by
$n \ge 1$
, denote by
![]() $F_n$
the random map from
$F_n$
the random map from
![]() $\mathbf {I} = [0,1[$
to itself defined by
$\mathbf {I} = [0,1[$
to itself defined by
![]() ${F_n := f_{\eta _n} \circ \cdots \circ f_{\eta _1}}$
. By convention,
${F_n := f_{\eta _n} \circ \cdots \circ f_{\eta _1}}$
. By convention,
![]() $F_0$
is the identity map from
$F_0$
is the identity map from
![]() $\mathbf {I}$
to
$\mathbf {I}$
to
![]() $\mathbf {I}$
. To prove Theorem 1, we use a coupling argument: given
$\mathbf {I}$
. To prove Theorem 1, we use a coupling argument: given
![]() $(y,y') \in \mathbf {I}^2$
, we study the processes
$(y,y') \in \mathbf {I}^2$
, we study the processes
![]() $((F_n(y),F_n(y'))_{n \ge 0}$
. These processes are Markov chains on
$((F_n(y),F_n(y'))_{n \ge 0}$
. These processes are Markov chains on
![]() $\mathbf {I}^2$
whose transition probabilities are given by
$\mathbf {I}^2$
whose transition probabilities are given by
These transition probabilities are closely related to the set
![]() $B_\theta = [0,\theta [ \times [\theta ,1[ \cup [\theta , 1[ \times [0,\theta [$
(see Figure 2 in §2.2). The key step in the proof is to show that the set
$B_\theta = [0,\theta [ \times [\theta ,1[ \cup [\theta , 1[ \times [0,\theta [$
(see Figure 2 in §2.2). The key step in the proof is to show that the set
![]() $B_\theta $
is visited more and more rarely.
$B_\theta $
is visited more and more rarely.

Figure 2 Probability transitions from different points
![]() $(y,y')$
. The probability associated to each arrow is
$(y,y')$
. The probability associated to each arrow is
![]() $1/2$
. The set
$1/2$
. The set
![]() $B_\theta $
is the union of the shaded rectangles. When
$B_\theta $
is the union of the shaded rectangles. When
![]() $(y,y') \in B_\theta $
, only one coordinate moves, so the transitions are parallel to the axis. When
$(y,y') \in B_\theta $
, only one coordinate moves, so the transitions are parallel to the axis. When
![]() $(y,y') \in B_\theta ^c$
, the same translation
$(y,y') \in B_\theta ^c$
, the same translation
![]() $\mathrm {Id}$
or
$\mathrm {Id}$
or
![]() $T_{-\theta }$
is applied to both coordinates, so the transitions are parallel to the diagonal.
$T_{-\theta }$
is applied to both coordinates, so the transitions are parallel to the diagonal.
Proposition 2. For every
![]() $(y,y') \in \mathbf {I}^2$
,
$(y,y') \in \mathbf {I}^2$
,
 $$ \begin{align*}\frac{1}{n} \sum_{k=0}^{n-1} {\mathbf 1}_{B_\theta}(F_k(y),F_k(y')) \to 0 \quad\text{almost surely as } n \to +\infty.\end{align*} $$
$$ \begin{align*}\frac{1}{n} \sum_{k=0}^{n-1} {\mathbf 1}_{B_\theta}(F_k(y),F_k(y')) \to 0 \quad\text{almost surely as } n \to +\infty.\end{align*} $$
1.4 Deriving Theorem 1 from Proposition 2
We explain the final arguments now that Proposition 2 has been established.
First, we prove that if
![]() $\pi $
is an invariant probability with regard to kernel K, then
$\pi $
is an invariant probability with regard to kernel K, then
![]() $\pi $
is carried by D, the diagonal of
$\pi $
is carried by D, the diagonal of
![]() $\mathbf {I}^2$
. Indeed, by stationarity, one has, for every
$\mathbf {I}^2$
. Indeed, by stationarity, one has, for every
![]() $n \ge 1$
,
$n \ge 1$
,
 $$ \begin{align*}\int_{\mathbf{I}^2}{\mathbf 1}_{B_\theta}((y,y'))\,{\mathrm{d}}\pi(y,y') = \int_{\mathbf{I}^2}\mathbf{E}\bigg[ \frac{1}{n} \sum_{k=0}^{n-1} {\mathbf 1}_{B_\theta}((F_k(y),F_k(y'))) \bigg]\, {\mathrm{d}}\pi(y,y').\end{align*} $$
$$ \begin{align*}\int_{\mathbf{I}^2}{\mathbf 1}_{B_\theta}((y,y'))\,{\mathrm{d}}\pi(y,y') = \int_{\mathbf{I}^2}\mathbf{E}\bigg[ \frac{1}{n} \sum_{k=0}^{n-1} {\mathbf 1}_{B_\theta}((F_k(y),F_k(y'))) \bigg]\, {\mathrm{d}}\pi(y,y').\end{align*} $$
In the right-hand side, the function integrated with regard to
![]() $\pi $
takes values in
$\pi $
takes values in
![]() $[0,1]$
and goes to zero everywhere as n goes to infinity. Hence, Lebesgue dominated convergence applies. Passing to the limit, we get
$[0,1]$
and goes to zero everywhere as n goes to infinity. Hence, Lebesgue dominated convergence applies. Passing to the limit, we get
![]() $\pi (B_\theta ) = 0$
. Since all future orbits under the action of
$\pi (B_\theta ) = 0$
. Since all future orbits under the action of
![]() $T_{-\theta }$
are dense in
$T_{-\theta }$
are dense in
![]() $\mathbf {I}$
, every Markov chain with transition kernel K starting from anywhere in
$\mathbf {I}$
, every Markov chain with transition kernel K starting from anywhere in
![]() $D^c$
reaches the set
$D^c$
reaches the set
![]() $B_\theta $
with positive probability (precise bounds on the number of steps will be given in §2). Thus,
$B_\theta $
with positive probability (precise bounds on the number of steps will be given in §2). Thus,
![]() $\pi (D^c) = 0$
.
$\pi (D^c) = 0$
.
Next, by enlarging, if necessary, the probability space on which the Markov chain
![]() $Y := (Y_n)_{n \in \mathbb {Z}y}$
is defined, we can construct a copy
$Y := (Y_n)_{n \in \mathbb {Z}y}$
is defined, we can construct a copy
![]() $Y' := (Y^{\prime }_n)_{n \in \mathbb {Z}}$
such that Y and
$Y' := (Y^{\prime }_n)_{n \in \mathbb {Z}}$
such that Y and
![]() $Y'$
are independent and identically distributed conditionally on
$Y'$
are independent and identically distributed conditionally on
![]() $\eta := (\eta _n)_{n \in \mathbb {Z}}$
. Since the process
$\eta := (\eta _n)_{n \in \mathbb {Z}}$
. Since the process
![]() $((Y_n,Y^{\prime }_n))_{n \in \mathbb {Z}}$
thus obtained is a stationary Markov chain with transition kernel K, it lives almost surely on D, so the processes
$((Y_n,Y^{\prime }_n))_{n \in \mathbb {Z}}$
thus obtained is a stationary Markov chain with transition kernel K, it lives almost surely on D, so the processes
![]() $Y=Y'$
almost surely. And since
$Y=Y'$
almost surely. And since
![]() $\mathcal {L}((Y,Y')|\eta ) = \mathcal {L}(Y|\eta ) \otimes \mathcal {L}(Y|\eta )$
almost surely, the conditional law
$\mathcal {L}((Y,Y')|\eta ) = \mathcal {L}(Y|\eta ) \otimes \mathcal {L}(Y|\eta )$
almost surely, the conditional law
![]() $\mathcal {L}(Y|\eta )$
is almost surely a Dirac mass, so Y is almost surely a deterministic function of the process
$\mathcal {L}(Y|\eta )$
is almost surely a Dirac mass, so Y is almost surely a deterministic function of the process
![]() $\eta $
.
$\eta $
.
Remember that, for every
![]() $n \in \mathbb {Z}$
, the random variable
$n \in \mathbb {Z}$
, the random variable
![]() $\eta _n$
is independent of
$\eta _n$
is independent of
![]() $\mathcal {F}^{\xi ,Y}_{n-1}$
. Given
$\mathcal {F}^{\xi ,Y}_{n-1}$
. Given
![]() $n \in \mathbb {Z}$
, the sequence
$n \in \mathbb {Z}$
, the sequence
![]() $(\eta _n)_{k \ge n+1}$
is independent of
$(\eta _n)_{k \ge n+1}$
is independent of
![]() $\mathcal {F}^{\xi ,Y}_n$
and therefore of the sub-
$\mathcal {F}^{\xi ,Y}_n$
and therefore of the sub-
![]() $\sigma $
-field
$\sigma $
-field
![]() $\sigma (Y_n) \vee \sigma ((\eta _n)_{k \le n})$
. Hence, one has, almost surely,
$\sigma (Y_n) \vee \sigma ((\eta _n)_{k \le n})$
. Hence, one has, almost surely,
so
![]() $Y_n$
is almost surely a measurable function of the process
$Y_n$
is almost surely a measurable function of the process
![]() $(\eta _n)_{k \le n}$
. Theorem 1 follows.
$(\eta _n)_{k \le n}$
. Theorem 1 follows.
1.5 Plan of the paper
In §2, we introduce the main tools and Lemmas involved to prove Proposition 2: continued fraction expansions, the three gap theorem and bounds for hitting and return times under the action of
![]() $T_{-\theta }$
.
$T_{-\theta }$
.
In §3, we prove Proposition 2.
In §4, we explain how the proof must be adapted to get a constructive proof that
![]() $[T_{\theta },T_{\theta }^{-1}]$
is Bernoulli.
$[T_{\theta },T_{\theta }^{-1}]$
is Bernoulli.
In §5, we consider related questions that are still open.
2 Tools
In this section, we present the techniques and preliminary results involved to prove Proposition 2. Our results heavily rely on the three gap theorem.
2.1 Three gap theorem and consequences
Let
![]() $(x_n)_{n \ge 0}$
be the sequence defined by
$(x_n)_{n \ge 0}$
be the sequence defined by
![]() $x_n := T_\theta ^n(0) = n\theta - \lfloor n\theta \rfloor $
. The well-known three gap theorem states that, for every
$x_n := T_\theta ^n(0) = n\theta - \lfloor n\theta \rfloor $
. The well-known three gap theorem states that, for every
![]() $n \ge 1$
, the intervals defined by the subdivision
$n \ge 1$
, the intervals defined by the subdivision
![]() $(x_k)_{0 \le k \le n-1}$
have at most three different lengths. We shall use a very precise statement of the three gap theorem, involving the continued fraction expansion
$(x_k)_{0 \le k \le n-1}$
have at most three different lengths. We shall use a very precise statement of the three gap theorem, involving the continued fraction expansion
![]() $\theta = [0;a_1,a_2,\ldots ]$
. Let us recall some classical facts. A more complete exposition can be found in [Reference Khintchine5].
$\theta = [0;a_1,a_2,\ldots ]$
. Let us recall some classical facts. A more complete exposition can be found in [Reference Khintchine5].
Set
![]() $a_0=\lfloor \theta \rfloor = 0$
and define two sequences
$a_0=\lfloor \theta \rfloor = 0$
and define two sequences
![]() $(p_k)_{k \ge -2}$
and
$(p_k)_{k \ge -2}$
and
![]() $(q_k)_{k \ge -2}$
of integers by
$(q_k)_{k \ge -2}$
of integers by
![]() $p_{-2}=0$
,
$p_{-2}=0$
,
![]() $q_{-2}=1$
,
$q_{-2}=1$
,
![]() $p_{-1}=1$
,
$p_{-1}=1$
,
![]() $q_{-1}=0$
, and, for every
$q_{-1}=0$
, and, for every
![]() $k \ge 0$
,
$k \ge 0$
,
Moreover,
![]() $p_k$
and
$p_k$
and
![]() $q_k$
are relatively prime since
$q_k$
are relatively prime since
![]() $p_kq_{k-1}-q_kp_{k-1} = (-1)^{k-1}$
.
$p_kq_{k-1}-q_kp_{k-1} = (-1)^{k-1}$
.
The fractions
![]() $(p_k/q_k)_{k \ge 0}$
are the convergents of
$(p_k/q_k)_{k \ge 0}$
are the convergents of
![]() $\theta $
. The following inequalities hold.
$\theta $
. The following inequalities hold.
In particular, the difference
![]() $\theta - p_k/q_k$
has the same sign as
$\theta - p_k/q_k$
has the same sign as
![]() $(-1)^k$
and
$(-1)^k$
and
 $$ \begin{align*}\frac{a_{k+2}}{q_kq_{k+2}} = \bigg|\frac{p_{k+2}}{q_{k+2}} - \frac{p_k}{q_k}\bigg| < \bigg|\theta - \frac{p_k}{q_k}\bigg| < \bigg|\frac{p_{k+1}}{q_{k+1}} - \frac{p_k}{q_k}\bigg| = \frac{1}{q_kq_{k+1}}.\end{align*} $$
$$ \begin{align*}\frac{a_{k+2}}{q_kq_{k+2}} = \bigg|\frac{p_{k+2}}{q_{k+2}} - \frac{p_k}{q_k}\bigg| < \bigg|\theta - \frac{p_k}{q_k}\bigg| < \bigg|\frac{p_{k+1}}{q_{k+1}} - \frac{p_k}{q_k}\bigg| = \frac{1}{q_kq_{k+1}}.\end{align*} $$
Hence, the sequence
![]() $(p_k/q_k)_{n \ge 0}$
converges to
$(p_k/q_k)_{n \ge 0}$
converges to
![]() $\theta $
.
$\theta $
.
For every
![]() $k \ge -1$
, set
$k \ge -1$
, set
![]() $\ell _k = (-1)^k(q_k\theta -p_k) = |q_k\theta -p_k|$
. In particular,
$\ell _k = (-1)^k(q_k\theta -p_k) = |q_k\theta -p_k|$
. In particular,
![]() $\ell _{-1} = 1$
,
$\ell _{-1} = 1$
,
![]() $\ell _0 = \theta $
and
$\ell _0 = \theta $
and
![]() $\ell _1 = 1 - \lfloor 1/\theta \rfloor \theta \le 1-\theta $
. Since, for every
$\ell _1 = 1 - \lfloor 1/\theta \rfloor \theta \le 1-\theta $
. Since, for every
![]() $k \ge 0$
,
$k \ge 0$
,
the sequence
![]() $(\ell _k)_{k \ge -1}$
is decreasing. For every
$(\ell _k)_{k \ge -1}$
is decreasing. For every
![]() $k \ge 1$
, we have
$k \ge 1$
, we have
![]() $\ell _k = -a_k \ell _{k-1} + \ell _{k-2}$
, so
$\ell _k = -a_k \ell _{k-1} + \ell _{k-2}$
, so
![]() $a_k = \lfloor \ell _{k-2}/\ell _{k-1}\rfloor $
.
$a_k = \lfloor \ell _{k-2}/\ell _{k-1}\rfloor $
.
We can now give a precise statement of the three gap theorem. The formulation below is close to the formulation given by Alessandri and Berthé [Reference Alessandri and Berthé1].
Theorem 3. Let
![]() $n \ge 1$
. Set
$n \ge 1$
. Set
![]() $n = bq_k+q_{k-1}+r$
, where
$n = bq_k+q_{k-1}+r$
, where
![]() $k \ge 0$
,
$k \ge 0$
,
![]() $b \in [1,a_{k+1}]$
and
$b \in [1,a_{k+1}]$
and
![]() ${r \in [0,q_k]}$
are integers. Then the points
${r \in [0,q_k]}$
are integers. Then the points
![]() $(x_i)_{0 \le i \le n-1}$
split
$(x_i)_{0 \le i \le n-1}$
split
![]() $\mathbf {I}$
into n intervals:
$\mathbf {I}$
into n intervals:
-
•
 $n-q_k = (b-1)q_k+q_{k-1}+r$
intervals with length
$n-q_k = (b-1)q_k+q_{k-1}+r$
intervals with length
 $\ell _k$
;
$\ell _k$
; -
•
 $q_k-r$
intervals with length
$q_k-r$
intervals with length
 $\ell _{k-1}-(b-1)\ell _k$
; and
$\ell _{k-1}-(b-1)\ell _k$
; and -
• r intervals with length
 $\ell _{k-1}-b\ell _k$
.
$\ell _{k-1}-b\ell _k$
.
Remark 4. Each positive integer n can be written as above. The decomposition is unique if we require that
![]() $r \le q_k-1$
. In this case:
$r \le q_k-1$
. In this case:
-
• k is the largest non-negative integer such that
 $q_k+q_{k-1} \le n$
, so
$q_k+q_{k-1} \le n$
, so
 $q_k+q_{k-1} \le n < q_{k+1}+q_k = (a_{k+1}+1)q_k+q_{k-1}$
;
$q_k+q_{k-1} \le n < q_{k+1}+q_k = (a_{k+1}+1)q_k+q_{k-1}$
; -
• b is the integer part of
 $(n-q_{k-1})/q_k$
, so
$(n-q_{k-1})/q_k$
, so
 $1 \le b \le a_{k+1}$
; and
$1 \le b \le a_{k+1}$
; and -
•
 $r=(n-q_{k-1})-bq_k$
, so
$r=(n-q_{k-1})-bq_k$
, so
 $0 \le r \le q_{k-1}-1$
.
$0 \le r \le q_{k-1}-1$
.
Under the assumptions of Theorem 3, we have
![]() $\ell _{k-1}-(b-1)\ell _k = (\ell _{k-1}-b\ell _k)+\ell _k$
. Moreover,
$\ell _{k-1}-(b-1)\ell _k = (\ell _{k-1}-b\ell _k)+\ell _k$
. Moreover,
![]() $\ell _{k-1}-b\ell _k<\ell _k$
if and only if
$\ell _{k-1}-b\ell _k<\ell _k$
if and only if
![]() $b=a_k$
. From these observations, we deduce the following consequences.
$b=a_k$
. From these observations, we deduce the following consequences.
Corollary 5. Fix
![]() $n \ge 1$
, and consider the n sub-intervals of
$n \ge 1$
, and consider the n sub-intervals of
![]() $\mathbf {I}$
defined by the subdivision
$\mathbf {I}$
defined by the subdivision
![]() $(x_i)_{0 \le i \le n-1}$
.
$(x_i)_{0 \le i \le n-1}$
.
-
• If
 $bq_k+q_{k-1} \le n < (b+1)q_k+q_{k-1}$
with
$bq_k+q_{k-1} \le n < (b+1)q_k+q_{k-1}$
with
 $k \ge 0$
and
$k \ge 0$
and
 $b \in [1,a_{k+1}]$
, the greatest length is
$b \in [1,a_{k+1}]$
, the greatest length is
 $\ell _{k-1}-(b-1)\ell _k$
.
$\ell _{k-1}-(b-1)\ell _k$
. -
• If
 $q_k < n \le q_{k+1}$
, the smallest length is
$q_k < n \le q_{k+1}$
, the smallest length is
 $\min \{\|i\theta \| : i \in [1,n-1]\} = \ell _k$
.
$\min \{\|i\theta \| : i \in [1,n-1]\} = \ell _k$
.
We can now answer precisely the following two questions. Given a semi-open subinterval J of
![]() $\mathbf {I}$
, what is the maximal number of iterations of
$\mathbf {I}$
, what is the maximal number of iterations of
![]() $T_{-\theta }$
to reach J from anywhere in
$T_{-\theta }$
to reach J from anywhere in
![]() $\mathbf {I}$
? What is the minimal number of iterations of
$\mathbf {I}$
? What is the minimal number of iterations of
![]() $T_{-\theta }$
necessary to return in J from anywhere in J?
$T_{-\theta }$
necessary to return in J from anywhere in J?
Corollary 6. Let J be a semi-open subinterval of
![]() $\mathbf {I}$
, modulo
$\mathbf {I}$
, modulo
![]() $1$
, namely,
$1$
, namely,
![]() $J = [\alpha ,\beta [$
with
$J = [\alpha ,\beta [$
with
![]() $0 \le \alpha < \beta \le 1$
(with length
$0 \le \alpha < \beta \le 1$
(with length
![]() $|J| = \beta -\alpha $
) or
$|J| = \beta -\alpha $
) or
![]() $J = [\alpha ,1[ \cup [0,\beta [$
with
$J = [\alpha ,1[ \cup [0,\beta [$
with
![]() $0 \le \beta < \alpha \le 1$
(with length
$0 \le \beta < \alpha \le 1$
(with length
![]() $|J| = 1+\beta -\alpha $
).
$|J| = 1+\beta -\alpha $
).
-
• Let
 $k \ge 0$
be the least integer such that
$k \ge 0$
be the least integer such that
 $\ell _k+\ell _{k+1} \le |J|$
, and let
$\ell _k+\ell _{k+1} \le |J|$
, and let
 $b \in [1,a_{k+1}]$
be the least integer such that
$b \in [1,a_{k+1}]$
be the least integer such that
 $\ell _{k-1}-(b-1)\ell _k \le |J|$
. This integer is well defined since
$\ell _{k-1}-(b-1)\ell _k \le |J|$
. This integer is well defined since
 $\ell _{k-1}-(a_{k+1}-1)\ell _k = \ell _k+\ell _{k+1}$
. Then
$\ell _{k-1}-(a_{k+1}-1)\ell _k = \ell _k+\ell _{k+1}$
. Then
 $bq_k+q_{k-1}-1$
iterations of
$bq_k+q_{k-1}-1$
iterations of
 $T_{-\theta }$
are sufficient to reach J from anywhere in
$T_{-\theta }$
are sufficient to reach J from anywhere in
 $\mathbf {I}$
, and this bound is optimal.
$\mathbf {I}$
, and this bound is optimal. -
• Let
 $k \ge 0$
be the least integer such that
$k \ge 0$
be the least integer such that
 $\ell _k \le |J|$
. For every
$\ell _k \le |J|$
. For every
 $y \in J$
, the first integer
$y \in J$
, the first integer
 $m(y) \ge 1$
such that
$m(y) \ge 1$
such that
 $T_{-\theta }^{m(y)}(y) \in J$
is at least equal to
$T_{-\theta }^{m(y)}(y) \in J$
is at least equal to
 $q_k$
.
$q_k$
.
Proof. We are searching for the least non-negative integer m such that
 $$ \begin{align} \bigcup_{k=0}^m T_\theta^k(J) = \mathbf{I}. \end{align} $$
$$ \begin{align} \bigcup_{k=0}^m T_\theta^k(J) = \mathbf{I}. \end{align} $$
By rotation, one may assume that
![]() $J = [0,|J|[$
. In this case, for every
$J = [0,|J|[$
. In this case, for every
![]() $k \ge 0$
,
$k \ge 0$
,
 $$ \begin{align*}T_\theta^k(J) = \begin{cases} [x_k,x_k+|J|[ & \text{if } x_k+|J| \le 1, \\ [x_k,1[ \cup [0,x_k+|J|-1[ & \text{if } x_k+|J|> 1. \end{cases}\end{align*} $$
$$ \begin{align*}T_\theta^k(J) = \begin{cases} [x_k,x_k+|J|[ & \text{if } x_k+|J| \le 1, \\ [x_k,1[ \cup [0,x_k+|J|-1[ & \text{if } x_k+|J|> 1. \end{cases}\end{align*} $$
Therefore, equality 1 holds if and only if the greatest length of the sub-intervals of
![]() $\mathbf {I}$
defined by the subdivision
$\mathbf {I}$
defined by the subdivision
![]() $(x_k)_{0 \le k \le m}$
is at most
$(x_k)_{0 \le k \le m}$
is at most
![]() $|J|$
. Thus, the first item follows from Corollary 5.
$|J|$
. Thus, the first item follows from Corollary 5.
Next, given
![]() $y \in J$
, we are searching for the least integer
$y \in J$
, we are searching for the least integer
![]() $m(y) \ge 1$
such that
$m(y) \ge 1$
such that
![]() ${T_{-\theta }^{m(y)}(y) \in J}$
, which implies that
${T_{-\theta }^{m(y)}(y) \in J}$
, which implies that
Denoting by
![]() $k \ge 0$
the least integer such that
$k \ge 0$
the least integer such that
![]() $\ell _k \le |J|$
, we derive
$\ell _k \le |J|$
, we derive
![]() $m(y) \ge q_k$
by Corollary 5.
$m(y) \ge q_k$
by Corollary 5.
2.2 A Markov chain on
 $\mathbf {I}^2$
$\mathbf {I}^2$
In this section, we study the Markov chains on
![]() $\mathbf {I}^2$
with kernel K. Our purpose is to give upper bounds on the entrance time in the set
$\mathbf {I}^2$
with kernel K. Our purpose is to give upper bounds on the entrance time in the set
![]() $B_\theta = [0,\theta [ \times [\theta ,1[ \cup [\theta ,1[ \times [0,\theta [$
.
$B_\theta = [0,\theta [ \times [\theta ,1[ \cup [\theta ,1[ \times [0,\theta [$
.
The transition probabilities can be also written as
Note that the transition probabilities from any
![]() $(y,y') \in B_\theta ^c$
preserve the difference
$(y,y') \in B_\theta ^c$
preserve the difference
![]() $y'-y$
modulo
$y'-y$
modulo
![]() $1$
. See Figure 2.
$1$
. See Figure 2.
Since D is absorbing and has no intersection with
![]() $B_\theta $
, the set
$B_\theta $
, the set
![]() $B_\theta $
cannot be reached from D. But the set
$B_\theta $
cannot be reached from D. But the set
![]() $B_\theta $
can be reached from any
$B_\theta $
can be reached from any
![]() $(y,y') \in D^c$
. We set
$(y,y') \in D^c$
. We set
Note that we have always
![]() $T_{y,y'} \ge t_{y,y'}$
, and that
$T_{y,y'} \ge t_{y,y'}$
, and that
![]() $t_{y,y'}$
and
$t_{y,y'}$
and
![]() $T_{y,y'}$
are null whenever
$T_{y,y'}$
are null whenever
![]() $(y,y')$
is in
$(y,y')$
is in
![]() $B_\theta $
. Moreover,
$B_\theta $
. Moreover,
For every real number
![]() $\delta $
, we denote by
$\delta $
, we denote by
the shortest distance from
![]() $\delta $
to
$\delta $
to
![]() $\mathbb {Z}y$
.
$\mathbb {Z}y$
.
Informally, we want to show that the times
![]() $t_{y,y'}$
and
$t_{y,y'}$
and
![]() $T_{y,y'}$
are small when
$T_{y,y'}$
are small when
![]() $\|y'-y\|$
is far from
$\|y'-y\|$
is far from
![]() $0$
and that they are ‘often’ big when
$0$
and that they are ‘often’ big when
![]() $\|y'-y\|$
is close to
$\|y'-y\|$
is close to
![]() $0$
. The restriction ‘often’ cannot be removed since
$0$
. The restriction ‘often’ cannot be removed since
![]() $t_{\theta -\varepsilon _1,\theta +\varepsilon _2}=0$
for every
$t_{\theta -\varepsilon _1,\theta +\varepsilon _2}=0$
for every
![]() $\varepsilon _1 \in ~]0,\theta ]$
and
$\varepsilon _1 \in ~]0,\theta ]$
and
![]() $\varepsilon _2 \in [0,1-\theta [$
. See Figure 3.
$\varepsilon _2 \in [0,1-\theta [$
. See Figure 3.

Figure 3 Entrance time in
![]() $B_\theta $
from any point under the action of the map
$B_\theta $
from any point under the action of the map
![]() $(y,y') \mapsto (T_{-\theta }(y),T_{-\theta }(y'))$
. Points far from the diagonal have low entrance time.
$(y,y') \mapsto (T_{-\theta }(y),T_{-\theta }(y'))$
. Points far from the diagonal have low entrance time.
Next, we prove a useful lemma.
Lemma 7. Let
![]() $y \in \mathbb {R}$
. There exists a unique sequence
$y \in \mathbb {R}$
. There exists a unique sequence
![]() $(\zeta ^y_n)_{n \ge 1}$
of independent uniform Bernoulli random variables such that, for every integer
$(\zeta ^y_n)_{n \ge 1}$
of independent uniform Bernoulli random variables such that, for every integer
![]() $n \ge 0$
,
$n \ge 0$
,
Proof. The uniqueness holds since
![]() $T_{-\theta }(y') \ne y'$
for every
$T_{-\theta }(y') \ne y'$
for every
![]() $y' \in \mathbf {I}$
. To prove the existence, we construct a sequence
$y' \in \mathbf {I}$
. To prove the existence, we construct a sequence
![]() $(\zeta ^y_n)_{n \ge 1}$
of random variables by setting, for every
$(\zeta ^y_n)_{n \ge 1}$
of random variables by setting, for every
![]() $n \ge 1$
,
$n \ge 1$
,
For every
![]() $n \ge 0$
, set
$n \ge 0$
, set
![]() $\mathcal {F}_n := \sigma (\eta _1,\ldots ,\eta _n)$
, with the convention
$\mathcal {F}_n := \sigma (\eta _1,\ldots ,\eta _n)$
, with the convention
![]() $\mathcal {F}_0 = \{\emptyset ,\Omega \}$
.
$\mathcal {F}_0 = \{\emptyset ,\Omega \}$
.
By construction,
![]() $\zeta ^y_n$
is an
$\zeta ^y_n$
is an
![]() $\mathcal {F}_n$
-measurable Bernoulli random variable, which is uniform and independent of
$\mathcal {F}_n$
-measurable Bernoulli random variable, which is uniform and independent of
![]() $\mathcal {F}_{n-1}$
since
$\mathcal {F}_{n-1}$
since
Moreover, a computation distinguishing two cases whether
![]() $F_{n-1}(y) < \theta $
or
$F_{n-1}(y) < \theta $
or
![]() $F_{n-1}(y) \ge \theta $
yields
$F_{n-1}(y) \ge \theta $
yields
The proof is complete.
Lemma 8. Assume that
![]() $0<\theta <1/2$
. Let y and
$0<\theta <1/2$
. Let y and
![]() $y'$
be two different points in
$y'$
be two different points in
![]() $\mathbf {I}$
.
$\mathbf {I}$
.
The time
![]() $t_{y,y'}$
is finite. More precisely, let
$t_{y,y'}$
is finite. More precisely, let
![]() $k \ge 0$
be the least integer such that
$k \ge 0$
be the least integer such that
![]() ${\ell _k+\ell _{k+1} \le \|y'-y\|}$
, and
${\ell _k+\ell _{k+1} \le \|y'-y\|}$
, and
![]() $b \in [1,a_{k+1}]$
the least integer such that
$b \in [1,a_{k+1}]$
the least integer such that
![]() $\ell _{k-1}-(b-1)\ell _k \le \|y'-y\|$
. Then
$\ell _{k-1}-(b-1)\ell _k \le \|y'-y\|$
. Then
![]() $t_{y,y'} \le bq_k+q_{k-1}-2$
if
$t_{y,y'} \le bq_k+q_{k-1}-2$
if
![]() $\|y'-y\| \le \theta $
and
$\|y'-y\| \le \theta $
and
![]() $t_{y,y'} \le q_1-1$
otherwise.
$t_{y,y'} \le q_1-1$
otherwise.
The random variable
![]() $T_{y,y'}$
is binomial negative, with parameters
$T_{y,y'}$
is binomial negative, with parameters
![]() $t_{y,y'}$
and
$t_{y,y'}$
and
![]() $1/2$
. In particular,
$1/2$
. In particular,
![]() $\mathbf {E}[T_{y,y'}] = 2t_{y,y'}$
.
$\mathbf {E}[T_{y,y'}] = 2t_{y,y'}$
.
Proof. Let
![]() $\delta = \|y'-y\|$
. Since y and
$\delta = \|y'-y\|$
. Since y and
![]() $y'$
play the same role, we may—and we do—assume that
$y'$
play the same role, we may—and we do—assume that
![]() $y' = T_\delta (y)$
.
$y' = T_\delta (y)$
.
We use the sequence
![]() $(\zeta ^y_n)_{n \ge 1}$
introduced in Lemma 7 and abbreviate the notation into
$(\zeta ^y_n)_{n \ge 1}$
introduced in Lemma 7 and abbreviate the notation into
![]() $(\zeta _n)_{n \ge 1}$
.
$(\zeta _n)_{n \ge 1}$
.
For every integer
![]() $n \ge 0$
,
$n \ge 0$
,
For every integer
![]() $n \in [0,T_{y,y'}-1]$
, the two points
$n \in [0,T_{y,y'}-1]$
, the two points
![]() $F_n(y')$
and
$F_n(y')$
and
![]() $F_n(y')$
belong to the same interval
$F_n(y')$
belong to the same interval
![]() $[0,\theta [$
or
$[0,\theta [$
or
![]() $[\theta ,1[$
, so
$[\theta ,1[$
, so
![]() $F_{n+1}(y') = T_{-\theta }^{\zeta _n}(F_n(y')) \equiv F_n(y')-\zeta _n\theta \,\mod \!\!\: 1$
. By recursion, we get
$F_{n+1}(y') = T_{-\theta }^{\zeta _n}(F_n(y')) \equiv F_n(y')-\zeta _n\theta \,\mod \!\!\: 1$
. By recursion, we get
and
Hence,
 $$ \begin{align*} T_{y,y'} &= \inf\{n \ge 0 : ( F_n(y),T_{\delta}((F_n(y)) ) \in B_\theta\} \\ &= \inf\{n \ge 0 : ( T_{-\theta}^{\zeta_1+\cdots+\zeta_n}(y), T_{\delta}(T_{-\theta}^{\zeta_1+\cdots+\zeta_n}(y)) ) \in B_\theta\} \\ &= \inf\{n \ge 0 : \zeta_1+\cdots+\zeta_n = t_{y,y'}\}. \end{align*} $$
$$ \begin{align*} T_{y,y'} &= \inf\{n \ge 0 : ( F_n(y),T_{\delta}((F_n(y)) ) \in B_\theta\} \\ &= \inf\{n \ge 0 : ( T_{-\theta}^{\zeta_1+\cdots+\zeta_n}(y), T_{\delta}(T_{-\theta}^{\zeta_1+\cdots+\zeta_n}(y)) ) \in B_\theta\} \\ &= \inf\{n \ge 0 : \zeta_1+\cdots+\zeta_n = t_{y,y'}\}. \end{align*} $$
Since
![]() $(\zeta _n)_{n \ge 1}$
is a sequence of independent uniform Bernoulli random variables, the random variable
$(\zeta _n)_{n \ge 1}$
is a sequence of independent uniform Bernoulli random variables, the random variable
![]() $T_{y,y'}$
is negative binomial, with parameters
$T_{y,y'}$
is negative binomial, with parameters
![]() $t_{y,y'}$
and
$t_{y,y'}$
and
![]() $1/2$
.
$1/2$
.
If
![]() $\delta \le \theta $
, then, for every
$\delta \le \theta $
, then, for every
![]() $x \in \mathbf {I}$
,
$x \in \mathbf {I}$
,
Thus,
![]() $t_{y,y'} = \inf \{n \ge 0 : T_{-\theta }^n(y) \in [\theta -\delta ,\theta [ \cup [1-\delta ,1[\}$
. By Corollary 6, at most
$t_{y,y'} = \inf \{n \ge 0 : T_{-\theta }^n(y) \in [\theta -\delta ,\theta [ \cup [1-\delta ,1[\}$
. By Corollary 6, at most
![]() ${bq_k+q_{k-1}-1}$
iterations of the map
${bq_k+q_{k-1}-1}$
iterations of the map
![]() $T_{-\theta }$
are sufficient to reach each one of the intervals
$T_{-\theta }$
are sufficient to reach each one of the intervals
![]() $[\theta -\delta ,\theta [$
or
$[\theta -\delta ,\theta [$
or
![]() $[1-\delta ,1[$
from y. But these two intervals are disjoint since
$[1-\delta ,1[$
from y. But these two intervals are disjoint since
![]() $0<\theta -\delta <\theta < 1/2<1-\delta <1$
. Hence,
$0<\theta -\delta <\theta < 1/2<1-\delta <1$
. Hence,
![]() $t_{y,y'} \le bq_k+q_{k-1}-2$
.
$t_{y,y'} \le bq_k+q_{k-1}-2$
.
If
![]() $\delta>\theta $
, then, for every
$\delta>\theta $
, then, for every
![]() $x \in \mathbf {I}$
,
$x \in \mathbf {I}$
,
Thus,
![]() $T = \inf \{n \ge 0 : F_n(y) \in [0,\theta [ \cup [1-\delta ,1-\delta +\theta [\}$
. By Corollary 6 applied with
$T = \inf \{n \ge 0 : F_n(y) \in [0,\theta [ \cup [1-\delta ,1-\delta +\theta [\}$
. By Corollary 6 applied with
![]() $k=1$
and
$k=1$
and
![]() $b=1$
, at most
$b=1$
, at most
![]() $q_1$
iterations of the map
$q_1$
iterations of the map
![]() $T_{-\theta }$
are sufficient to reach each one of the intervals
$T_{-\theta }$
are sufficient to reach each one of the intervals
![]() $[0,\theta [$
or
$[0,\theta [$
or
![]() $[1-\delta ,1-\delta +\theta [$
from y. But these two intervals are disjoint since
$[1-\delta ,1-\delta +\theta [$
from y. But these two intervals are disjoint since
![]() $0<\theta <1/2<1-\delta <1-\delta +\theta <1$
. Hence,
$0<\theta <1/2<1-\delta <1-\delta +\theta <1$
. Hence,
![]() $t_{y,y'} \le q_1-1$
.
$t_{y,y'} \le q_1-1$
.
The proof is complete.
Corollary 9. Let y and
![]() $y'$
be in
$y'$
be in
![]() $\mathbf {I}$
and let
$\mathbf {I}$
and let
![]() $k \ge 1$
be an integer such that
$k \ge 1$
be an integer such that
![]() $\ell _{k-1} \le \|y'-y\|$
. Then
$\ell _{k-1} \le \|y'-y\|$
. Then
![]() $t_{y,y'} \le q_k+q_{k-1}-2$
.
$t_{y,y'} \le q_k+q_{k-1}-2$
.
Proof. By Lemma 8, if
![]() $\theta \le \|y'-y\|$
, then
$\theta \le \|y'-y\|$
, then
![]() $t_{y,y'} \le q_1-1 \le q_k+q_{k-1}-2$
.
$t_{y,y'} \le q_1-1 \le q_k+q_{k-1}-2$
.
From now on, we focus on the case where
![]() $\|y'-y\| \le \theta $
. Observe that
$\|y'-y\| \le \theta $
. Observe that
If
![]() $\|y'-y\| < \ell _{k-1}+\ell _k$
, then Lemma 8 applied to the integers k and
$\|y'-y\| < \ell _{k-1}+\ell _k$
, then Lemma 8 applied to the integers k and
![]() $b=1$
yields
$b=1$
yields
![]() $t_{y,y'} \le q_k+q_{k-1}-2$
.
$t_{y,y'} \le q_k+q_{k-1}-2$
.
Otherwise,
![]() $k \ge 2$
since
$k \ge 2$
since
![]() $\ell _{k-1} < \ell _{k-1}+\ell _k \le \|y'-y\| \le \theta = \ell _0$
. Furthermore, the least integer
$\ell _{k-1} < \ell _{k-1}+\ell _k \le \|y'-y\| \le \theta = \ell _0$
. Furthermore, the least integer
![]() $k' \ge 1$
such that
$k' \ge 1$
such that
![]() $\ell _{k'}+\ell _{k'+1} \le \|y'-y\|$
is at most
$\ell _{k'}+\ell _{k'+1} \le \|y'-y\|$
is at most
![]() $k-1$
and Lemma 8 applies to the integers
$k-1$
and Lemma 8 applies to the integers
![]() $k' \ge 1$
and some
$k' \ge 1$
and some
![]() $b \in [1,a_{k'+1}]$
, so
$b \in [1,a_{k'+1}]$
, so
Hence, in all cases, we get
![]() $t_{y,y'} \le q_k+q_{k-1}-2$
.
$t_{y,y'} \le q_k+q_{k-1}-2$
.
2.3 A time-changed symmetric random walk
For every real number x, denote by
![]() ${\overline {x} = x+\mathbb {Z}}$
its equivalence class in
${\overline {x} = x+\mathbb {Z}}$
its equivalence class in
![]() $\mathbb {R}/\mathbb {Z}$
. Then Lemma 8 and the strong Markov property show that the process
$\mathbb {R}/\mathbb {Z}$
. Then Lemma 8 and the strong Markov property show that the process
![]() $(\overline {F_n(y')-F_n(y)})_{n \ge 0}$
is a time-changed symmetric random walk on
$(\overline {F_n(y')-F_n(y)})_{n \ge 0}$
is a time-changed symmetric random walk on
![]() $\mathbb {R}/\mathbb {Z}$
with steps
$\mathbb {R}/\mathbb {Z}$
with steps
![]() $\pm \overline {\theta }$
.
$\pm \overline {\theta }$
.
Lemma 10. For every
![]() $n \ge 0$
, set
$n \ge 0$
, set
![]() $\mathcal {F}_n = \sigma (\eta _1,\ldots ,\eta _n)$
, with the convention
$\mathcal {F}_n = \sigma (\eta _1,\ldots ,\eta _n)$
, with the convention
![]() $\mathcal {F}_0 = \{\emptyset ,\Omega \}$
. Consider the non-decreasing process
$\mathcal {F}_0 = \{\emptyset ,\Omega \}$
. Consider the non-decreasing process
![]() $(A_n)_{n \ge 0}$
defined by
$(A_n)_{n \ge 0}$
defined by
 $$ \begin{align*}A_n := \sum_{k=0}^{n-1} {\mathbf 1}_{B_\theta} (F_k(y),F_k(y')) \quad\textrm{with the convention } A_0=0,\end{align*} $$
$$ \begin{align*}A_n := \sum_{k=0}^{n-1} {\mathbf 1}_{B_\theta} (F_k(y),F_k(y')) \quad\textrm{with the convention } A_0=0,\end{align*} $$
and set
![]() $A_\infty :=\lim _n A_n$
. Consider its inverse
$A_\infty :=\lim _n A_n$
. Consider its inverse
![]() $(N_a)_{a \ge 0}$
, defined by
$(N_a)_{a \ge 0}$
, defined by
On the event
![]() $[N_a<+\infty ] = [a \le A_\infty ]$
, set
$[N_a<+\infty ] = [a \le A_\infty ]$
, set
 $$ \begin{align*}\Delta N_a := N_{a+1}-N_a \quad\text{and}\quad W_a := \sum_{b=1}^a (2\zeta^y_{N_b}-1),\end{align*} $$
$$ \begin{align*}\Delta N_a := N_{a+1}-N_a \quad\text{and}\quad W_a := \sum_{b=1}^a (2\zeta^y_{N_b}-1),\end{align*} $$
with the notation of Lemma 7.
-
(1) For every
 $n \ge 0$
,
$n \ge 0$
,  $$ \begin{align*}F_n(y')-F_n(y) \equiv y'-y + \theta W_{A_n} \,\mod\!\!\: 1.\end{align*} $$
$$ \begin{align*}F_n(y')-F_n(y) \equiv y'-y + \theta W_{A_n} \,\mod\!\!\: 1.\end{align*} $$
-
(2) The random times
 $(N_a-1)_{a \ge 1}$
are stopping times in the filtration
$(N_a-1)_{a \ge 1}$
are stopping times in the filtration
 $(\mathcal {F}_n)_{n \ge 0}$
.
$(\mathcal {F}_n)_{n \ge 0}$
. -
(3) The process
 $(W_a)_{a \ge 0}$
is a simple symmetric random walk on
$(W_a)_{a \ge 0}$
is a simple symmetric random walk on
 $\mathbb {Z}$
, with possibly finite lifetime
$\mathbb {Z}$
, with possibly finite lifetime
 $A_\infty $
. More precisely, for every positive integer
$A_\infty $
. More precisely, for every positive integer
 $a \ge 0$
, conditionally on the event
$a \ge 0$
, conditionally on the event
 $[A_\infty \ge a]$
, the increments
$[A_\infty \ge a]$
, the increments
 $W_1-W_0,\ldots ,W_a-W_{a-1}$
are independent and uniform on
$W_1-W_0,\ldots ,W_a-W_{a-1}$
are independent and uniform on
 $\{-1,1\}$
.
$\{-1,1\}$
. -
(4) One has
 $A_\infty = A_{T^D_{y,y'}}$
, where
$A_\infty = A_{T^D_{y,y'}}$
, where
 $T^D_{y,y'} := \inf \{n \ge 0 : F_n(y) = F_n(y')\}$
. If
$T^D_{y,y'} := \inf \{n \ge 0 : F_n(y) = F_n(y')\}$
. If
 $y'-y \in \mathbb {Z}+\theta \mathbb {Z}$
, then
$y'-y \in \mathbb {Z}+\theta \mathbb {Z}$
, then
 $A_\infty $
is almost surely finite. Otherwise,
$A_\infty $
is almost surely finite. Otherwise,
 $A_\infty $
is infinite.
$A_\infty $
is infinite. -
(5) Assume that
 $y'-y \notin \mathbb {Z}y+\theta \mathbb {Z}$
. Conditionally on the process
$y'-y \notin \mathbb {Z}y+\theta \mathbb {Z}$
. Conditionally on the process
 $(((F_{N_a}(y), F_{N_a}(y')))_{a \ge 0}$
, the random variables
$(((F_{N_a}(y), F_{N_a}(y')))_{a \ge 0}$
, the random variables
 $(\Delta N_a)_{a \ge 0}$
are independent and each
$(\Delta N_a)_{a \ge 0}$
are independent and each
 $\Delta N_a - 1$
is negative binomial with parameters
$\Delta N_a - 1$
is negative binomial with parameters
 $t_{F_{N_a}(y),F_{N_a}(y')}$
and
$t_{F_{N_a}(y),F_{N_a}(y')}$
and
 $1/2$
.
$1/2$
.
Proof. We use the sequence
![]() $(\zeta _n)_{n \ge 1}:=(\zeta ^y_n)_{n \ge 1}$
introduced in Lemma 7 and define
$(\zeta _n)_{n \ge 1}:=(\zeta ^y_n)_{n \ge 1}$
introduced in Lemma 7 and define
![]() $(\zeta ^{\prime }_n)_{n \ge 1}:=(\zeta ^{y'}_n)_{n \ge 1}$
in the same way. By construction,
$(\zeta ^{\prime }_n)_{n \ge 1}:=(\zeta ^{y'}_n)_{n \ge 1}$
in the same way. By construction,
Then
A recursion yields, for every
![]() $n \ge 0$
,
$n \ge 0$
,
 $$ \begin{align*}F_n(y')-F_n(y) \equiv y'-y+M_n \theta \,\mod\!\!\: 1 \quad\text{where } M_n := \sum_{k=1}^n(\zeta_k-\zeta^{\prime}_k),\end{align*} $$
$$ \begin{align*}F_n(y')-F_n(y) \equiv y'-y+M_n \theta \,\mod\!\!\: 1 \quad\text{where } M_n := \sum_{k=1}^n(\zeta_k-\zeta^{\prime}_k),\end{align*} $$
with the convention
![]() $M_0=0$
. For every
$M_0=0$
. For every
![]() $k \ge 1$
,
$k \ge 1$
,
![]() $\zeta ^{\prime }_k = 1-\zeta _k$
if
$\zeta ^{\prime }_k = 1-\zeta _k$
if
![]() $(F_{k-1}(y),F_{k-1}(y')) \in B_\theta $
, whereas
$(F_{k-1}(y),F_{k-1}(y')) \in B_\theta $
, whereas
![]() $\zeta ^{\prime }_k = \zeta _k$
if
$\zeta ^{\prime }_k = \zeta _k$
if
![]() $(F_{k-1}(y),F_{k-1}(y')) \in B_\theta ^c$
, so
$(F_{k-1}(y),F_{k-1}(y')) \in B_\theta ^c$
, so
 $$ \begin{align*} \zeta_k-\zeta^{\prime}_k &= {\mathbf 1}_{B_\theta} (F_{k-1}(y),F_{k-1}(y')) \times (2\zeta_k-1) \\ &= (A_k-A_{k-1}) \times (2\zeta_k-1). \end{align*} $$
$$ \begin{align*} \zeta_k-\zeta^{\prime}_k &= {\mathbf 1}_{B_\theta} (F_{k-1}(y),F_{k-1}(y')) \times (2\zeta_k-1) \\ &= (A_k-A_{k-1}) \times (2\zeta_k-1). \end{align*} $$
By definition, for every
![]() $a \ge 0$
, on the event
$a \ge 0$
, on the event
![]() $[N_a<+\infty ]$
, the process
$[N_a<+\infty ]$
, the process
![]() $(A_n)_{n \ge 0}$
remains constant and equal to a during the time interval
$(A_n)_{n \ge 0}$
remains constant and equal to a during the time interval
![]() $[N_a,N_{a+1}-1]$
. Hence,
$[N_a,N_{a+1}-1]$
. Hence,
 $$ \begin{align*} M_n = \sum_{k=1}^n (M_k-M_{k-1}) = \sum_{b=1}^{A_n} (M_{N_b}-M_{N_b-1}) = \sum_{b=1}^{A_n} (2\zeta_{N_b}-1) = W_{A_n}. \end{align*} $$
$$ \begin{align*} M_n = \sum_{k=1}^n (M_k-M_{k-1}) = \sum_{b=1}^{A_n} (M_{N_b}-M_{N_b-1}) = \sum_{b=1}^{A_n} (2\zeta_{N_b}-1) = W_{A_n}. \end{align*} $$
Item (1) follows.
The process
![]() $(A_n)_{n \ge 0}$
defined by
$(A_n)_{n \ge 0}$
defined by
 $$ \begin{align*}A_n = \sum_{k=0}^{n-1} {\mathbf 1}_{B_\theta} (F_k(y),F_k(y'))\end{align*} $$
$$ \begin{align*}A_n = \sum_{k=0}^{n-1} {\mathbf 1}_{B_\theta} (F_k(y),F_k(y'))\end{align*} $$
is
![]() $(\mathcal {F}_n)_{n \ge 0}$
-predictable: the random variable
$(\mathcal {F}_n)_{n \ge 0}$
-predictable: the random variable
![]() $A_0=0$
is constant and, for every
$A_0=0$
is constant and, for every
![]() $n \ge 1$
, the random variable
$n \ge 1$
, the random variable
![]() $A_n$
is
$A_n$
is
![]() $\mathcal {F}_{n-1}$
-measurable.
$\mathcal {F}_{n-1}$
-measurable.
For every
![]() $a \ge 0$
, the random variable
$a \ge 0$
, the random variable
![]() $N_a$
is a stopping time in the filtration
$N_a$
is a stopping time in the filtration
![]() $(\mathcal {F}_n)_{n \ge 0}$
. If
$(\mathcal {F}_n)_{n \ge 0}$
. If
![]() $a \ge 1$
, the random variable
$a \ge 1$
, the random variable
![]() $N_a-1$
is still a stopping time since, for every
$N_a-1$
is still a stopping time since, for every
![]() $n \ge 0$
,
$n \ge 0$
,
Item (2) follows.
Let
![]() $a \ge 0$
. The event
$a \ge 0$
. The event
![]() $[N_a<+\infty ] = [N_a-1<+\infty ]$
belongs to
$[N_a<+\infty ] = [N_a-1<+\infty ]$
belongs to
![]() $\mathcal {F}_{N_a-1}$
. On this event, the sequence
$\mathcal {F}_{N_a-1}$
. On this event, the sequence
![]() $(\tilde {\eta }_{n})_{n \ge 0}:=(\eta _{N_a+n})_{n \ge 0}$
is an independent and identically distributed sequence of uniform Bernoulli random variables and is independent of
$(\tilde {\eta }_{n})_{n \ge 0}:=(\eta _{N_a+n})_{n \ge 0}$
is an independent and identically distributed sequence of uniform Bernoulli random variables and is independent of
![]() $\mathcal {F}_{N_a-1}$
. Therefore, we know the following.
$\mathcal {F}_{N_a-1}$
. Therefore, we know the following.
-
• The Bernoulli random variable
 $\zeta _{N_a} = (\eta _{N_a}+{\mathbf 1}_{[0,\theta [}(F_{N_a-1}(y)))\,\mod \!\!\: 2$
is uniform, independent of
$\zeta _{N_a} = (\eta _{N_a}+{\mathbf 1}_{[0,\theta [}(F_{N_a-1}(y)))\,\mod \!\!\: 2$
is uniform, independent of
 $\mathcal {F}_{N_a-1}$
and
$\mathcal {F}_{N_a-1}$
and
 $\mathcal {F}_{N_a}$
-measurable. Thus the random variable
$\mathcal {F}_{N_a}$
-measurable. Thus the random variable
 $W_a-W_{a-1} = 2\zeta _{N_a}-1$
is uniform on
$W_a-W_{a-1} = 2\zeta _{N_a}-1$
is uniform on
 $\{-1,1\}$
, independent of
$\{-1,1\}$
, independent of
 $\mathcal {F}_{N_a-1}$
and
$\mathcal {F}_{N_a-1}$
and
 $\mathcal {F}_{N_a}$
-measurable. Item (3) follows.
$\mathcal {F}_{N_a}$
-measurable. Item (3) follows. -
• The random variable
 $(Y,Y') :=(F_{N_a}(y),F_{N_a}(y'))$
is
$(Y,Y') :=(F_{N_a}(y),F_{N_a}(y'))$
is
 $\mathcal {F}_{N_a}$
-measurable.
$\mathcal {F}_{N_a}$
-measurable. -
• The process
 $(\tilde {F}_{n})_{n \ge 0}$
, defined by
$(\tilde {F}_{n})_{n \ge 0}$
, defined by
 $\tilde {F}_n := f_{\tilde {\eta }_n} \circ \cdots \circ f_{\tilde {\eta }_1}$
, is independent of
$\tilde {F}_n := f_{\tilde {\eta }_n} \circ \cdots \circ f_{\tilde {\eta }_1}$
, is independent of
 $\mathcal {F}_{N_a}$
and has the same law as
$\mathcal {F}_{N_a}$
and has the same law as
 $(F_{n})_{n \ge 0}$
.
$(F_{n})_{n \ge 0}$
.
Observe that, with obvious notation,
Hence, conditionally on
![]() $\mathcal {F}_{N_a}$
and on the event
$\mathcal {F}_{N_a}$
and on the event
![]() $[N_a<+\infty ] \cap [Y \ne Y']$
, the random variable
$[N_a<+\infty ] \cap [Y \ne Y']$
, the random variable
![]() $\Delta {N_a}-1$
is almost surely finite and negative binomial with parameters
$\Delta {N_a}-1$
is almost surely finite and negative binomial with parameters
![]() $t_{Y,Y'}$
and
$t_{Y,Y'}$
and
![]() $1/2$
. Item (5) follows. Moreover, for every
$1/2$
. Item (5) follows. Moreover, for every
![]() $a \ge 0$
, we have almost surely
$a \ge 0$
, we have almost surely
Hence, almost surely,
During each time interval
![]() $[N_a,N_{a+1}-1]$
, the process
$[N_a,N_{a+1}-1]$
, the process
![]() $(F_n(y')-F_n(y))$
remains constant modulo 1 and the process
$(F_n(y')-F_n(y))$
remains constant modulo 1 and the process
![]() $(A_n)_{n \ge 0}$
remains constant and equal to a. Thus,
$(A_n)_{n \ge 0}$
remains constant and equal to a. Thus,
Since, for every
![]() $n \ge 0$
,
$n \ge 0$
,
![]() $F_n(y') - F_n(y) \equiv y'-y + \theta W_{A_n} \,\mod \!\!\: 1$
, the difference
$F_n(y') - F_n(y) \equiv y'-y + \theta W_{A_n} \,\mod \!\!\: 1$
, the difference
![]() ${F_n(y') - F_n(y)}$
remains in the coset
${F_n(y') - F_n(y)}$
remains in the coset
![]() $y'-y + \theta \mathbb {Z} + \mathbb {Z}$
. Therefore, the time
$y'-y + \theta \mathbb {Z} + \mathbb {Z}$
. Therefore, the time
![]() $T^D_{y,y'}$
cannot be finite unless
$T^D_{y,y'}$
cannot be finite unless
![]() $y'-y \in \theta \mathbb {Z} + \mathbb {Z}$
. Conversely, if
$y'-y \in \theta \mathbb {Z} + \mathbb {Z}$
. Conversely, if
![]() $y'-y \in \theta \mathbb {Z} + \mathbb {Z}$
, then
$y'-y \in \theta \mathbb {Z} + \mathbb {Z}$
, then
![]() $T^D_{y,y'}$
is almost surely finite by recurrence of the symmetric simple random walk on
$T^D_{y,y'}$
is almost surely finite by recurrence of the symmetric simple random walk on
![]() $\mathbb {Z}$
. Item (4) follows.
$\mathbb {Z}$
. Item (4) follows.
By density of the subgroup
![]() $\theta \mathbb {Z} + \mathbb {Z}$
in
$\theta \mathbb {Z} + \mathbb {Z}$
in
![]() $\mathbb {R}$
and by recurrence of the symmetric simple random walk on
$\mathbb {R}$
and by recurrence of the symmetric simple random walk on
![]() $\mathbb {Z}$
, we derive the following consequence.
$\mathbb {Z}$
, we derive the following consequence.
Corollary 11. Let y and
![]() $y'$
be two points in
$y'$
be two points in
![]() $\mathbf {I}$
such that
$\mathbf {I}$
such that
![]() $y'-y \notin \mathbb {Z}+\theta \mathbb {Z}$
. Then, almost surely,
$y'-y \notin \mathbb {Z}+\theta \mathbb {Z}$
. Then, almost surely,
Proof. We use the notation and the results of Lemma 10. The recurrence of the symmetric simple random walk on
![]() $\mathbb {Z}$
and the density of the subgroup
$\mathbb {Z}$
and the density of the subgroup
![]() $\theta \mathbb {Z} + \mathbb {Z}$
in
$\theta \mathbb {Z} + \mathbb {Z}$
in
![]() $\mathbb {R}$
yields
$\mathbb {R}$
yields
Since the quantities
![]() $\|F_n(y')-F_n(y)\|$
are all positive, the greatest lower bound of the sequence
$\|F_n(y')-F_n(y)\|$
are all positive, the greatest lower bound of the sequence
![]() $(\|F_n(y')-F_n(y)\|)_{n \ge 0}$
is not achieved and is therefore a lower limit. We argue in the same way with the least upper bound.
$(\|F_n(y')-F_n(y)\|)_{n \ge 0}$
is not achieved and is therefore a lower limit. We argue in the same way with the least upper bound.
To prove that the Cesàro averages of the sequence
![]() $(\|F_n(y')-F_n(y)\|)_{n \ge 0}$
tend to zero, we observe that the time change in the process
$(\|F_n(y')-F_n(y)\|)_{n \ge 0}$
tend to zero, we observe that the time change in the process
![]() $(W_{A_n})_{n \ge 0}$
slows down the random walk much more when the difference is
$(W_{A_n})_{n \ge 0}$
slows down the random walk much more when the difference is
![]() $\|y'-y\|$
is small. Indeed, Corollary 9 shows that if
$\|y'-y\|$
is small. Indeed, Corollary 9 shows that if
![]() $\|y'-y\|$
is not close to zero, then the process
$\|y'-y\|$
is not close to zero, then the process
![]() $((F_n(y),F_n(y'))_{n \ge 0}$
reaches
$((F_n(y),F_n(y'))_{n \ge 0}$
reaches
![]() $B_\theta $
quickly, and the difference
$B_\theta $
quickly, and the difference
![]() $F_n(y')-F_n(y)$
changes immediately after.
$F_n(y')-F_n(y)$
changes immediately after.
Conversely, if
![]() $\|y'-y\|$
is small, we hope that it will take a long time for the process
$\|y'-y\|$
is small, we hope that it will take a long time for the process
![]() $((F_n(y),F_n(y')))_{n \ge n_0}$
to reach
$((F_n(y),F_n(y')))_{n \ge n_0}$
to reach
![]() $B_\theta $
. During this time, the difference
$B_\theta $
. During this time, the difference
![]() $F_n(y')-F_n(y)$
remains unchanged. Yet, we may be unlucky, so the times
$F_n(y')-F_n(y)$
remains unchanged. Yet, we may be unlucky, so the times
![]() $t_{y,y'}$
and
$t_{y,y'}$
and
![]() $T_{y,y'}$
may be small. Fortunately, the distance
$T_{y,y'}$
may be small. Fortunately, the distance
![]() $\|F_n(y')-F_n(y)\|$
is close to
$\|F_n(y')-F_n(y)\|$
is close to
![]() $\theta $
at time
$\theta $
at time
![]() $N_1 = T_{y,y'}+1$
, so it will change soon. With probability
$N_1 = T_{y,y'}+1$
, so it will change soon. With probability
![]() $1/2$
, we will get
$1/2$
, we will get
![]() $W_2=0$
, so
$W_2=0$
, so
![]() $\|F_{N_2}(y')-F_{N_2}(y)\| = \|y'-y\|$
will be small, and this time the distance
$\|F_{N_2}(y')-F_{N_2}(y)\| = \|y'-y\|$
will be small, and this time the distance
![]() $\|F_n(y')-F_n(y)\|$
will remain unchanged during a long time. The role of the next Lemma is to provide a lower bound for this time.
$\|F_n(y')-F_n(y)\|$
will remain unchanged during a long time. The role of the next Lemma is to provide a lower bound for this time.
Lemma 12. Let y and
![]() $y'$
be two distinct points in
$y'$
be two distinct points in
![]() $\mathbf {I}$
such that
$\mathbf {I}$
such that
![]() $(y,y') \in [0,1-\theta [^2 \cup [\theta ,1[^2$
and
$(y,y') \in [0,1-\theta [^2 \cup [\theta ,1[^2$
and
![]() $\|y'-y\| < \ell _2$
. Let
$\|y'-y\| < \ell _2$
. Let
![]() $k \ge 3$
be the integer such that
$k \ge 3$
be the integer such that
![]() $\ell _k \le \|y'-y\| < \ell _{k-1}$
. Keep the notation of Lemma 10. Then
$\ell _k \le \|y'-y\| < \ell _{k-1}$
. Keep the notation of Lemma 10. Then
Before proving Lemma 12, it is important to note that all probability transitions
![]() $K((y,y'),\cdot )$
give full measure to the set
$K((y,y'),\cdot )$
give full measure to the set
![]() $[0,1-\theta [^2 \cup [\theta ,1[^2$
(see Figure 4). Hence, the additional hypothesis
$[0,1-\theta [^2 \cup [\theta ,1[^2$
(see Figure 4). Hence, the additional hypothesis
![]() $(y,y') \in [0,1-\theta [^2 \cup [\theta ,1[^2$
will not be a true restriction. Actually, this assumption could be removed by changing the lower bound into
$(y,y') \in [0,1-\theta [^2 \cup [\theta ,1[^2$
will not be a true restriction. Actually, this assumption could be removed by changing the lower bound into
![]() $q_k-q_2-q_1$
.
$q_k-q_2-q_1$
.

Figure 4 The squares
![]() $[0,\theta [ \times [1-\theta ,1[$
and
$[0,\theta [ \times [1-\theta ,1[$
and
![]() $[1-\theta ,1[ \times [0,\theta [$
cannot be reached from anywhere via the kernel K. If
$[1-\theta ,1[ \times [0,\theta [$
cannot be reached from anywhere via the kernel K. If
![]() $0<\delta <\theta $
, then
$0<\delta <\theta $
, then
![]() $B_\theta \cap \{(y,T_\delta (y)); y \in \mathbf {I}\}$
is the union of two ‘semi-open segments’, defined by
$B_\theta \cap \{(y,T_\delta (y)); y \in \mathbf {I}\}$
is the union of two ‘semi-open segments’, defined by
![]() $\theta -\delta \le y <\theta $
and
$\theta -\delta \le y <\theta $
and
![]() $1-\delta \le y <1$
. The second semi-open segment cannot be reached from anywhere via the kernel K and is the image of the first one by the map
$1-\delta \le y <1$
. The second semi-open segment cannot be reached from anywhere via the kernel K and is the image of the first one by the map
![]() $(y,y') \mapsto (T_{-\theta }(y),T_{-\theta }(y'))$
.
$(y,y') \mapsto (T_{-\theta }(y),T_{-\theta }(y'))$
.
Proof. The inequality
![]() $\Delta N_2-1 \ge t_{F_{N_2}(y),F_{N_2}(y')} \ge 0$
follows from item (5) of Lemma 10.
$\Delta N_2-1 \ge t_{F_{N_2}(y),F_{N_2}(y')} \ge 0$
follows from item (5) of Lemma 10.
The assumption
![]() $(y,y') \in [0,1-\theta [^2 \cup [\theta ,1[^2$
ensures that
$(y,y') \in [0,1-\theta [^2 \cup [\theta ,1[^2$
ensures that
![]() $(F_n(y),F_n(y'))$
belongs to
$(F_n(y),F_n(y'))$
belongs to
![]() $[0,1-\theta [^2 \cup [\theta ,1[^2$
not only for every
$[0,1-\theta [^2 \cup [\theta ,1[^2$
not only for every
![]() $n \ge 1$
, but also when
$n \ge 1$
, but also when
![]() $n=0$
.
$n=0$
.
Set
![]() $\delta = \|y'-y\|$
. By symmetry, we may assume that
$\delta = \|y'-y\|$
. By symmetry, we may assume that
![]() $y'-y \equiv \delta \,\mod \!\!\: 1$
, that is,
$y'-y \equiv \delta \,\mod \!\!\: 1$
, that is,
![]() ${y'=T_\delta (y)}$
. Hence, for every
${y'=T_\delta (y)}$
. Hence, for every
![]() $a \ge 0$
,
$a \ge 0$
,
![]() $F_{N_{a+1}-1}(y')-F_{N_{a+1}-1}(y) \equiv \delta + \theta W_a \,\mod \!\!\: 1$
.
$F_{N_{a+1}-1}(y')-F_{N_{a+1}-1}(y) \equiv \delta + \theta W_a \,\mod \!\!\: 1$
.
On the event
![]() $[W_2=0]$
, we have
$[W_2=0]$
, we have
Since the points
![]() $(F_{N_1-1}(y),F_{N_1-1}(y'))$
and
$(F_{N_1-1}(y),F_{N_1-1}(y'))$
and
![]() $(F_{N_3-1}(y),F_{N_3-1}(y'))$
belong at the same time to
$(F_{N_3-1}(y),F_{N_3-1}(y'))$
belong at the same time to
![]() $B_\theta $
and to
$B_\theta $
and to
![]() $[0,1-\theta [^2 \cup [\theta ,1[^2$
, we deduce that
$[0,1-\theta [^2 \cup [\theta ,1[^2$
, we deduce that
![]() $F_{N_1-1}(y)$
and
$F_{N_1-1}(y)$
and
![]() $F_{N_3-1}(y)$
belong to
$F_{N_3-1}(y)$
belong to
![]() $[\theta -\delta ,\theta [$
. But
$[\theta -\delta ,\theta [$
. But
![]() $F_{N_3-1}(y)$
is obtained from
$F_{N_3-1}(y)$
is obtained from
![]() $F_{N_1-1}(y)$
by applying the transformation
$F_{N_1-1}(y)$
by applying the transformation
![]() $T_{-\theta }$
exactly
$T_{-\theta }$
exactly
![]() $\zeta ^y_{N_1}+t_{F_{N_1}(y),F_{N_1}(y')}+\zeta ^y_{N_2}+t_{F_{N_2}(y),F_{N_2}(y')}$
times.
$\zeta ^y_{N_1}+t_{F_{N_1}(y),F_{N_1}(y')}+\zeta ^y_{N_2}+t_{F_{N_2}(y),F_{N_2}(y')}$
times.
On the event
![]() $[W_2=0]$
, we have
$[W_2=0]$
, we have
![]() $\zeta ^y_{N_1}+\zeta ^y_{N_2}=1$
, so Corollary 6 yields
$\zeta ^y_{N_1}+\zeta ^y_{N_2}=1$
, so Corollary 6 yields
But
![]() $F_{N_1}(y')-F_{N_1}(y) \equiv \delta \pm \theta \,\mod \!\!\: 1$
, so
$F_{N_1}(y')-F_{N_1}(y) \equiv \delta \pm \theta \,\mod \!\!\: 1$
, so
Corollary 9 yields
![]() $t_{F_{N_1}(y),F_{N_1}(y')} \le q_2+q_1-2$
.Thus,
$t_{F_{N_1}(y),F_{N_1}(y')} \le q_2+q_1-2$
.Thus,
The desired inequality follows.
2.4 Martingales and symmetric simple random walk on
 $\mathbb {Z}$
$\mathbb {Z}$
In this subsection, we establish three more results that which help us in the proof of Proposition 2. The first of them is a kind of law of large numbers.
Lemma 13. Let
![]() $(\mathcal {G}_n)_{n \ge 0}$
be a filtration of
$(\mathcal {G}_n)_{n \ge 0}$
be a filtration of
![]() $(\Omega ,\mathcal {A},\mathbf {P})$
and let
$(\Omega ,\mathcal {A},\mathbf {P})$
and let
![]() $(Z_n)_{n \ge 1}$
be a sequence of real random variables, bounded in
$(Z_n)_{n \ge 1}$
be a sequence of real random variables, bounded in
![]() $L^2(\mathbf {P})$
, and adapted to the filtration
$L^2(\mathbf {P})$
, and adapted to the filtration
![]() $(\mathcal {G}_n)_{n \ge 1}$
. Then
$(\mathcal {G}_n)_{n \ge 1}$
. Then
 $$ \begin{align*}\frac{1}{n} \sum_{k=1}^n (Z_k-\mathbf{E}[Z_k|\mathcal{G}_{n-1}] ) \to 0 \quad\textrm{almost surely as } n \to +\infty.\end{align*} $$
$$ \begin{align*}\frac{1}{n} \sum_{k=1}^n (Z_k-\mathbf{E}[Z_k|\mathcal{G}_{n-1}] ) \to 0 \quad\textrm{almost surely as } n \to +\infty.\end{align*} $$
Proof. For every
![]() $n \ge 0$
, let
$n \ge 0$
, let
 $$ \begin{align*}M_n = \sum_{k=1}^n \frac{1}{k} (Z_k-\mathbf{E}[Z_k|\mathcal{G}_{n-1}] ).\end{align*} $$
$$ \begin{align*}M_n = \sum_{k=1}^n \frac{1}{k} (Z_k-\mathbf{E}[Z_k|\mathcal{G}_{n-1}] ).\end{align*} $$
By construction, the sequence
![]() $(M_n)_{n \ge 0}$
is a square-integrable martingale in
$(M_n)_{n \ge 0}$
is a square-integrable martingale in
![]() $(\mathcal {G})_{n \ge 0}$
. The increments
$(\mathcal {G})_{n \ge 0}$
. The increments
![]() $M_k-M_{k-1}$
are pairwise orthogonal in
$M_k-M_{k-1}$
are pairwise orthogonal in
![]() $L^2(\mathbf {P})$
and
$L^2(\mathbf {P})$
and
 $$ \begin{align*} \sum_{k \ge 1} \|M_k-M_{k-1}\|_2^2 = \sum_{k \ge 1}\frac{1}{k^2} \|Z_k-\mathbf{E}[Z_k|\mathcal{G}_{n-1}] \|_2^2 \le \sum_{k \ge 1}\frac{1}{k^2} \|Z_k \|_2^2 < +\infty. \end{align*} $$
$$ \begin{align*} \sum_{k \ge 1} \|M_k-M_{k-1}\|_2^2 = \sum_{k \ge 1}\frac{1}{k^2} \|Z_k-\mathbf{E}[Z_k|\mathcal{G}_{n-1}] \|_2^2 \le \sum_{k \ge 1}\frac{1}{k^2} \|Z_k \|_2^2 < +\infty. \end{align*} $$
Hence, the martingale
![]() $(M_n)_{n \ge 0}$
is bounded in
$(M_n)_{n \ge 0}$
is bounded in
![]() $L^2(\mathbf {P})$
and it converges almost surely and in
$L^2(\mathbf {P})$
and it converges almost surely and in
![]() $L^2(\mathbf {P})$
to some real random variable
$L^2(\mathbf {P})$
to some real random variable
![]() $M_\infty $
.
$M_\infty $
.
 $$ \begin{align*} \frac{1}{n} \sum_{k=1}^n (Z_k-\mathbf{E}[Z_k|\mathcal{G}_{n-1}] ) &= \frac{1}{n} \sum_{k=1}^n k(M_k-M_{k-1}) \\ &= \frac{1}{n} \bigg(nM_n + \sum_{k=1}^{n-1} kM_k - M_0 - \sum_{k=1}^{n-1}(k+1)M_k \bigg) \\ &= M_n - \frac{1}{n} \sum_{k=1}^{n-1} M_k. \end{align*} $$
$$ \begin{align*} \frac{1}{n} \sum_{k=1}^n (Z_k-\mathbf{E}[Z_k|\mathcal{G}_{n-1}] ) &= \frac{1}{n} \sum_{k=1}^n k(M_k-M_{k-1}) \\ &= \frac{1}{n} \bigg(nM_n + \sum_{k=1}^{n-1} kM_k - M_0 - \sum_{k=1}^{n-1}(k+1)M_k \bigg) \\ &= M_n - \frac{1}{n} \sum_{k=1}^{n-1} M_k. \end{align*} $$
The conclusion follows from Cesàró’s lemma.
The second result is a refinement of the gambler’s ruin theorem [Reference Resnick10].
Lemma 14. Let
![]() $(W_n)_{n \ge 0}$
be a symmetric simple random walk on
$(W_n)_{n \ge 0}$
be a symmetric simple random walk on
![]() $\mathbb {Z}$
, that is,
$\mathbb {Z}$
, that is,
![]() $W_0=0$
and
$W_0=0$
and
![]() $(W_n-W_{n-1})_{n \ge 1}$
is an independent and identically distributed sequence of Rademacher random variables. Fix two non-negative integers a and b and set
$(W_n-W_{n-1})_{n \ge 1}$
is an independent and identically distributed sequence of Rademacher random variables. Fix two non-negative integers a and b and set
Then
![]() $\tau _{-a,b}<+\infty $
almost surely. Moreover:
$\tau _{-a,b}<+\infty $
almost surely. Moreover:
-
•
 $\mathbf {P}[W_{\tau _{-a,b}} = -a] = b/(a+b)$
and
$\mathbf {P}[W_{\tau _{-a,b}} = -a] = b/(a+b)$
and
 $\mathbf {P}[W_{\tau _{-a,b}} = b] = a/(a+b)$
;
$\mathbf {P}[W_{\tau _{-a,b}} = b] = a/(a+b)$
; -
•
 $\mathbf {E}[\tau _{-a,b}] = ab$
; and
$\mathbf {E}[\tau _{-a,b}] = ab$
; and -
• for every
 $\unicode{x3bb} \ge 0$
,
$\unicode{x3bb} \ge 0$
,
 $\mathbf {E}[(\cosh \unicode{x3bb} )^{-\tau _{-a,b}}] = \cosh ((({-a+b})/{2})\unicode{x3bb} ) / \cosh ((({a+b})/{2})\unicode{x3bb} ).$
$\mathbf {E}[(\cosh \unicode{x3bb} )^{-\tau _{-a,b}}] = \cosh ((({-a+b})/{2})\unicode{x3bb} ) / \cosh ((({a+b})/{2})\unicode{x3bb} ).$
Proof. One checks that the processes
![]() $(W_n)_{n \ge 0}$
,
$(W_n)_{n \ge 0}$
,
![]() $(W_n^2-n)_{n \ge 0}$
and
$(W_n^2-n)_{n \ge 0}$
and
![]() $(e^{\pm \unicode{x3bb} W_n}(\cosh \unicode{x3bb} )^{-n})_{n \ge 0}$
are martingales, and that the martingales
$(e^{\pm \unicode{x3bb} W_n}(\cosh \unicode{x3bb} )^{-n})_{n \ge 0}$
are martingales, and that the martingales
 $$ \begin{align*}(W_n)_{n \ge 0}, \quad \bigg( \bigg(W_n-\frac{b-a}{2}\bigg)^2-n \bigg)_{n \ge 0}, \quad \bigg(\cosh\bigg(\unicode{x3bb}\bigg(W_n-\frac{b-a}{2}\bigg)\bigg)(\cosh \unicode{x3bb})^{-n}\bigg)_{n \ge 0}\end{align*} $$
$$ \begin{align*}(W_n)_{n \ge 0}, \quad \bigg( \bigg(W_n-\frac{b-a}{2}\bigg)^2-n \bigg)_{n \ge 0}, \quad \bigg(\cosh\bigg(\unicode{x3bb}\bigg(W_n-\frac{b-a}{2}\bigg)\bigg)(\cosh \unicode{x3bb})^{-n}\bigg)_{n \ge 0}\end{align*} $$
are uniformly bounded on the time interval
![]() $[0,\tau _{-a,b}]$
. Hence, the optional stopping time theorem applies. Writing that the expectations at time
$[0,\tau _{-a,b}]$
. Hence, the optional stopping time theorem applies. Writing that the expectations at time
![]() $\tau _{-a,b}$
are equal to the expectations at time
$\tau _{-a,b}$
are equal to the expectations at time
![]() $0$
yields items (1), (2) and (3).
$0$
yields items (1), (2) and (3).
The third result states an equidistribution modulo 1.
Lemma 15. Let
![]() $(W_n)_{n \ge 0}$
be a symmetric simple random walk on
$(W_n)_{n \ge 0}$
be a symmetric simple random walk on
![]() $\mathbb {Z}y$
and let
$\mathbb {Z}y$
and let
![]() $\theta $
be any irrational number. Then, for every continuous
$\theta $
be any irrational number. Then, for every continuous
![]() $1$
-periodic function
$1$
-periodic function
![]() $f : \mathbb {R} \to \mathbf {C}$
,
$f : \mathbb {R} \to \mathbf {C}$
,
 $$ \begin{align*}\frac{1}{n}\sum_{k=0}^{n-1} f(\theta W_k) \to \int_0^1 f(x)\, {\mathrm{d}} x \quad\textrm{almost surely as } n \to +\infty.\end{align*} $$
$$ \begin{align*}\frac{1}{n}\sum_{k=0}^{n-1} f(\theta W_k) \to \int_0^1 f(x)\, {\mathrm{d}} x \quad\textrm{almost surely as } n \to +\infty.\end{align*} $$
Proof. Since the trigonometric polynomials form a dense subspace of the vector space of all continuous
![]() $1$
-periodic functions, we need only to prove the result when f is the function
$1$
-periodic functions, we need only to prove the result when f is the function
![]() $e_m : x \mapsto e^{i2\pi mx}$
for some
$e_m : x \mapsto e^{i2\pi mx}$
for some
![]() $m \in \mathbb {Z}$
. The case where
$m \in \mathbb {Z}$
. The case where
![]() $m=0$
is trivial, so we fix
$m=0$
is trivial, so we fix
![]() $m \ne 0$
.
$m \ne 0$
.
For every
![]() $n \ge 1$
, let
$n \ge 1$
, let
 $$ \begin{align*}S_n := \sum_{k=0}^{n-1} e^{i2\pi m\theta W_k}.\end{align*} $$
$$ \begin{align*}S_n := \sum_{k=0}^{n-1} e^{i2\pi m\theta W_k}.\end{align*} $$
Then
 $$ \begin{align*} |S_n|^2 = S_n \overline{S_n} = \sum_{k=0}^{n-1} \sum_{\ell=0}^{n-1}e^{i2\pi m\theta(W_k-W_\ell)}. \end{align*} $$
$$ \begin{align*} |S_n|^2 = S_n \overline{S_n} = \sum_{k=0}^{n-1} \sum_{\ell=0}^{n-1}e^{i2\pi m\theta(W_k-W_\ell)}. \end{align*} $$
Let
![]() $z = \mathbf {E}[e^{i2\pi m\theta (W_1-W_0)}] = \cos (2\pi m\theta )$
. Then
$z = \mathbf {E}[e^{i2\pi m\theta (W_1-W_0)}] = \cos (2\pi m\theta )$
. Then
![]() $z \in ~]-1,1[$
since
$z \in ~]-1,1[$
since
![]() $m \ne 0$
and
$m \ne 0$
and
![]() $\theta $
is irrational. By independent equidistribution of the increments of the random walk W, we derive
$\theta $
is irrational. By independent equidistribution of the increments of the random walk W, we derive
 $$ \begin{align*} \mathbf{E}[|S_n|^2] &= \sum_{k=0}^{n-1} \sum_{\ell=0}^{n-1} z^{|k-\ell|} = n + 2\sum_{d=1}^{n-1} (n-d)z^d \\ &\le n \bigg(1+2\sum_{d=1}^{n-1}|z|^d \bigg) \le n \frac{1+|z|}{1-|z|}. \end{align*} $$
$$ \begin{align*} \mathbf{E}[|S_n|^2] &= \sum_{k=0}^{n-1} \sum_{\ell=0}^{n-1} z^{|k-\ell|} = n + 2\sum_{d=1}^{n-1} (n-d)z^d \\ &\le n \bigg(1+2\sum_{d=1}^{n-1}|z|^d \bigg) \le n \frac{1+|z|}{1-|z|}. \end{align*} $$
Thus,
 $$ \begin{align*}\sum_{n=1}^{+\infty} \bigg\Vert \frac{1}{n^3}S_{n^3} \bigg\Vert_2 \le \sum_{n=1}^{+\infty} \bigg(\frac{1+|z|}{1-|z|}\bigg)^{-1/2} n^{-3/2}< +\infty.\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{+\infty} \bigg\Vert \frac{1}{n^3}S_{n^3} \bigg\Vert_2 \le \sum_{n=1}^{+\infty} \bigg(\frac{1+|z|}{1-|z|}\bigg)^{-1/2} n^{-3/2}< +\infty.\end{align*} $$
The series
![]() $\sum _n S_{n^3}/n^3$
is absolutely convergent in
$\sum _n S_{n^3}/n^3$
is absolutely convergent in
![]() $L^2(\mathbf {P})$
, so it converges almost surely and in
$L^2(\mathbf {P})$
, so it converges almost surely and in
![]() $L^2(\mathbf {P})$
. Therefore,
$L^2(\mathbf {P})$
. Therefore,
![]() $S_{n^3}/n^3 \to 0$
almost surely as
$S_{n^3}/n^3 \to 0$
almost surely as
![]() $n \to +\infty $
. To deduce that
$n \to +\infty $
. To deduce that
![]() $S_n/n \to 0$
almost surely as
$S_n/n \to 0$
almost surely as
![]() $n \to +\infty $
, it suffices to set
$n \to +\infty $
, it suffices to set
![]() $r_n = \lfloor n^{1/3} \rfloor $
and to note that
$r_n = \lfloor n^{1/3} \rfloor $
and to note that
3 Proof of Proposition 2
Let
![]() $y,y'$
be in
$y,y'$
be in
![]() $\mathbf {I}$
and let
$\mathbf {I}$
and let
![]() $\delta = y'-y$
. We use again the notation and the results contained in Lemma 10.
$\delta = y'-y$
. We use again the notation and the results contained in Lemma 10.
If
![]() $\delta \in \mathbb {Z}+\theta \mathbb {Z}$
, then, almost surely,
$\delta \in \mathbb {Z}+\theta \mathbb {Z}$
, then, almost surely,
![]() $F_n(y') - F_n(y)$
is null for all large enough n, so the conclusion holds.
$F_n(y') - F_n(y)$
is null for all large enough n, so the conclusion holds.
We now focus on the difficult case, when
![]() $\delta \notin \mathbb {Z}+\theta \mathbb {Z}$
. First, we prove the following Lemma.
$\delta \notin \mathbb {Z}+\theta \mathbb {Z}$
. First, we prove the following Lemma.
Lemma 16. Assume that
![]() $\delta \notin \mathbb {Z}+\theta \mathbb {Z}$
, and keep the notation of Lemma 10.
$\delta \notin \mathbb {Z}+\theta \mathbb {Z}$
, and keep the notation of Lemma 10.
-
(1) Consider the function g from
 $[0,1/2]$
to
$[0,1/2]$
to
 $[0,+\infty ]$
defined by
$[0,+\infty ]$
defined by
 $g(0)=+\infty $
and
$g(0)=+\infty $
and  $$ \begin{align*}g(r):= 1+(q_k+1-q_2-q_1)_+ \text{ whenever } \ell_k \le r < \ell_{k-1}.\end{align*} $$
$$ \begin{align*}g(r):= 1+(q_k+1-q_2-q_1)_+ \text{ whenever } \ell_k \le r < \ell_{k-1}.\end{align*} $$
This function g is non-increasing on
 $[0,1/2]$
and bounded below by
$[0,1/2]$
and bounded below by
 $1$
. Moreover, the integral of g on
$1$
. Moreover, the integral of g on
 $[0,1/2]$
is infinite.
$[0,1/2]$
is infinite. -
(2) Moreover,
 $$ \begin{align*}\text{ for all } a \ge 3, \quad \Delta N_a \ge g(\|\theta W_a\|) {\mathbf 1}_{[W_a=W_{a-2}]}.\end{align*} $$
$$ \begin{align*}\text{ for all } a \ge 3, \quad \Delta N_a \ge g(\|\theta W_a\|) {\mathbf 1}_{[W_a=W_{a-2}]}.\end{align*} $$
Proof. The sequence
![]() $(\ell _k)_{k \ge 0}$
is decreasing and the sequence
$(\ell _k)_{k \ge 0}$
is decreasing and the sequence
![]() $(q_k)_{k \ge 0}$
is non-decreasing. The monotonicity of g and h and the lower bounds follow. On each interval
$(q_k)_{k \ge 0}$
is non-decreasing. The monotonicity of g and h and the lower bounds follow. On each interval
![]() $[\ell _k,\ell _{k-1}[$
,
$[\ell _k,\ell _{k-1}[$
,
![]() $g(r) \ge q_k-q_3$
, and thus
$g(r) \ge q_k-q_3$
, and thus
 $$ \begin{align*}\int_0^{\ell_2}g(r) {\mathrm{d}} r \ge \sum_{k=3}^{+\infty}q_k(\ell_{k-1}-\ell_k) - q_3\ell_2.\end{align*} $$
$$ \begin{align*}\int_0^{\ell_2}g(r) {\mathrm{d}} r \ge \sum_{k=3}^{+\infty}q_k(\ell_{k-1}-\ell_k) - q_3\ell_2.\end{align*} $$
But
![]() $q_k\ell _{k-1} \ge 1/2$
for every
$q_k\ell _{k-1} \ge 1/2$
for every
![]() $k \ge 0$
and
$k \ge 0$
and
![]() $\ell _{k-1} \ge ({1+\sqrt {5}})/{2} \ell _k$
for at least one k among two consecutive k (since
$\ell _{k-1} \ge ({1+\sqrt {5}})/{2} \ell _k$
for at least one k among two consecutive k (since
![]() $\ell _{k-1} \ge \ell _k+\ell _{k+1}$
for every
$\ell _{k-1} \ge \ell _k+\ell _{k+1}$
for every
![]() $k \ge 0$
). Item (1) follows.
$k \ge 0$
). Item (1) follows.
Now, assume that
![]() $a \ge 3$
. Then
$a \ge 3$
. Then
![]() $N_{a-2} \ge a-2 \ge 1$
, so the point
$N_{a-2} \ge a-2 \ge 1$
, so the point
![]() $(Y,Y'):=(F_{N_{a-2}}(y), F_{N_{a-2}}(y'))$
belongs to
$(Y,Y'):=(F_{N_{a-2}}(y), F_{N_{a-2}}(y'))$
belongs to
![]() $[0,1-\theta [^2 \cup [\theta ,1[^2$
. The sequence
$[0,1-\theta [^2 \cup [\theta ,1[^2$
. The sequence
![]() $(\eta _{N_{a-2}+n})_{n \ge 0}$
is independent of
$(\eta _{N_{a-2}+n})_{n \ge 0}$
is independent of
![]() $(Y,Y')$
and has the same law as
$(Y,Y')$
and has the same law as
![]() $(\eta _n)_{n \ge 0}$
. Hence, we may apply Lemma 12 to
$(\eta _n)_{n \ge 0}$
. Hence, we may apply Lemma 12 to
![]() $(Y,Y')$
and the sequence
$(Y,Y')$
and the sequence
![]() $(\eta _{N_{a-2}+n})_{n \ge 0}$
instead of
$(\eta _{N_{a-2}+n})_{n \ge 0}$
instead of
![]() $(y,y')$
and
$(y,y')$
and
![]() $(\eta _n)_{n \ge 0}$
. We get
$(\eta _n)_{n \ge 0}$
. We get
Item (2) follows.
We now prove Proposition 2.
On each time interval
![]() $[N_a,N_{a+1}-1]$
, we have
$[N_a,N_{a+1}-1]$
, we have
![]() $A_n=a$
, so
$A_n=a$
, so
Hence, we only need to show that
![]() $N_a/a \to +\infty $
almost surely as
$N_a/a \to +\infty $
almost surely as
![]() $a \to +\infty $
. To do this, we observe that, for every
$a \to +\infty $
. To do this, we observe that, for every
![]() $a \ge 3$
,
$a \ge 3$
,
 $$ \begin{align*} \frac{N_a}{a} = \frac{1}{a} \sum_{b=0}^{a-1} \Delta N_b &\ge \frac{1}{a} \sum_{b=3}^{a-1} {\mathbf 1}_{[W_b=W_{b-2}]} g(\|\delta + \theta W_{b-2}\|) \\ &= \frac{1}{a} \sum_{k=2}^{a-2} {\mathbf 1}_{[W_{k+1}=W_{k-1}]} g(\|\delta + \theta W_{k-1}\|). \end{align*} $$
$$ \begin{align*} \frac{N_a}{a} = \frac{1}{a} \sum_{b=0}^{a-1} \Delta N_b &\ge \frac{1}{a} \sum_{b=3}^{a-1} {\mathbf 1}_{[W_b=W_{b-2}]} g(\|\delta + \theta W_{b-2}\|) \\ &= \frac{1}{a} \sum_{k=2}^{a-2} {\mathbf 1}_{[W_{k+1}=W_{k-1}]} g(\|\delta + \theta W_{k-1}\|). \end{align*} $$
Therefore, it is sufficient to prove that
 $$ \begin{align*}\frac{1}{a} \sum_{k=1}^a {\mathbf 1}_{[W_{k+1}=W_{k-1}]} g(\|\delta + \theta W_{k-1}\|) \to +\infty \quad\text{almost surely as } a \to +\infty.\end{align*} $$
$$ \begin{align*}\frac{1}{a} \sum_{k=1}^a {\mathbf 1}_{[W_{k+1}=W_{k-1}]} g(\|\delta + \theta W_{k-1}\|) \to +\infty \quad\text{almost surely as } a \to +\infty.\end{align*} $$
The positive function
![]() $x \mapsto g(\|\delta + x\|)$
can be written as the limit of a non-decreasing sequence of continuous
$x \mapsto g(\|\delta + x\|)$
can be written as the limit of a non-decreasing sequence of continuous
![]() $1$
-periodic functions. Given such functions, the sequence of their integrals on
$1$
-periodic functions. Given such functions, the sequence of their integrals on
![]() $[0,1]$
tends to infinity by Beppo Levi’s lemma.
$[0,1]$
tends to infinity by Beppo Levi’s lemma.
Thus, it suffices to prove that, for every continuous
![]() $1$
-periodic function
$1$
-periodic function
![]() $f : \mathbb {R} \to \mathbb {R}$
,
$f : \mathbb {R} \to \mathbb {R}$
,
 $$ \begin{align*}\frac{1}{a} \sum_{k=1}^a {\mathbf 1}_{[W_{k+1}=W_{k-1}]} f(\theta W_{k-1}) \to \frac{1}{2}\int_0^1 f(x)\, {\mathrm{d}} x\quad\text{almost surely as } a \to +\infty.\end{align*} $$
$$ \begin{align*}\frac{1}{a} \sum_{k=1}^a {\mathbf 1}_{[W_{k+1}=W_{k-1}]} f(\theta W_{k-1}) \to \frac{1}{2}\int_0^1 f(x)\, {\mathrm{d}} x\quad\text{almost surely as } a \to +\infty.\end{align*} $$
Since, for every
![]() $k \ge 1$
,
$k \ge 1$
,
![]() $\mathbf {P}[W_{k+1}=W_{k-1}|\mathcal {F}_{N_k}] = 1/2$
, Lemma 13 applied to the random variables
$\mathbf {P}[W_{k+1}=W_{k-1}|\mathcal {F}_{N_k}] = 1/2$
, Lemma 13 applied to the random variables
![]() $Z_k := {\mathbf 1}_{[W_{k+1}=W_{k-1}]} f(\theta W_{k+1}) = {\mathbf 1}_{[W_{k+1}=W_{k-1}]} f(\theta W_{k-1})$
and to the filtration
$Z_k := {\mathbf 1}_{[W_{k+1}=W_{k-1}]} f(\theta W_{k+1}) = {\mathbf 1}_{[W_{k+1}=W_{k-1}]} f(\theta W_{k-1})$
and to the filtration
![]() $(\mathcal {G}_k)_{k \ge 0} := (\mathcal {F}_{N_k})_{k \ge 0}$
yields
$(\mathcal {G}_k)_{k \ge 0} := (\mathcal {F}_{N_k})_{k \ge 0}$
yields
 $$ \begin{align*}\frac{1}{a} \sum_{k=1}^a \bigg( {\mathbf 1}_{[W_{k+1}=W_{k-1}]} f(\theta W_{k-1}) - \frac{1}{2} f(\theta W_{k-1}) \bigg) \to 0 \quad\textrm{almost surely as } n \to +\infty.\end{align*} $$
$$ \begin{align*}\frac{1}{a} \sum_{k=1}^a \bigg( {\mathbf 1}_{[W_{k+1}=W_{k-1}]} f(\theta W_{k-1}) - \frac{1}{2} f(\theta W_{k-1}) \bigg) \to 0 \quad\textrm{almost surely as } n \to +\infty.\end{align*} $$
But Lemma 15 yields
 $$ \begin{align*}\frac{1}{a}\sum_{k=1}^a f(\theta W_{k-1}) \to \int_0^1 f(x)\, {\mathrm{d}} x \quad\text{almost surely as } a \to +\infty.\end{align*} $$
$$ \begin{align*}\frac{1}{a}\sum_{k=1}^a f(\theta W_{k-1}) \to \int_0^1 f(x)\, {\mathrm{d}} x \quad\text{almost surely as } a \to +\infty.\end{align*} $$
Hence, the conclusion follows.
![]() $\square $
$\square $
4 Constructive proof that
 $[T_\theta ,T_\theta ^{-1}]$
is Bernoulli
$[T_\theta ,T_\theta ^{-1}]$
is Bernoulli
The strategy used for
![]() $[T_\theta ,\mathrm {Id}]$
also works for
$[T_\theta ,\mathrm {Id}]$
also works for
![]() $[T_\theta ,T_\theta ^{-1}]$
with some adaptations, which are often slight but in some places more substantial. Let us explain them.
$[T_\theta ,T_\theta ^{-1}]$
with some adaptations, which are often slight but in some places more substantial. Let us explain them.
We define
![]() $[T_\theta ,T_\theta ^{-1}]$
on the space
$[T_\theta ,T_\theta ^{-1}]$
on the space
![]() $\{-1,1\}^{\mathbb {Z}_+} \times \mathbf {I}$
with the same formula used to define
$\{-1,1\}^{\mathbb {Z}_+} \times \mathbf {I}$
with the same formula used to define
![]() $[T_\theta ,\mathrm {Id}]$
on the space
$[T_\theta ,\mathrm {Id}]$
on the space
![]() $\{0,1\}^{\mathbb {Z}_+} \times \mathbf {I}$
. In the probabilistic reformulation, we work with an independent and identically distributed sequence
$\{0,1\}^{\mathbb {Z}_+} \times \mathbf {I}$
. In the probabilistic reformulation, we work with an independent and identically distributed sequence
![]() $(\xi _n)_{n \in \mathbb {Z}}$
of Rademacher random variables. The process
$(\xi _n)_{n \in \mathbb {Z}}$
of Rademacher random variables. The process
![]() $(Y_n)_{n \in \mathbb {Z}}$
is a Markov chain on
$(Y_n)_{n \in \mathbb {Z}}$
is a Markov chain on
![]() $\mathbf {I}$
whose evolution is governed by
$\mathbf {I}$
whose evolution is governed by
![]() $(\xi _n)_{n \in \mathbb {Z}}$
through the recursion relation
$(\xi _n)_{n \in \mathbb {Z}}$
through the recursion relation
where
![]() $\xi _n$
is uniform on
$\xi _n$
is uniform on
![]() $\{-1,1\}$
and independent of
$\{-1,1\}$
and independent of
![]() $\mathcal {F}^{\xi ,Y}_{n-1}$
.
$\mathcal {F}^{\xi ,Y}_{n-1}$
.
For every
![]() $n \in \mathbb {Z}$
, the random variable
$n \in \mathbb {Z}$
, the random variable
is also uniform on
![]() $\{-1,1\}$
and independent of
$\{-1,1\}$
and independent of
![]() $\mathcal {F}^{\xi ,Y}_{n-1}$
, and the recursion relation can be written alternatively as
$\mathcal {F}^{\xi ,Y}_{n-1}$
, and the recursion relation can be written alternatively as
where the maps
![]() $f_{-1}$
and
$f_{-1}$
and
![]() $f_1$
from
$f_1$
from
![]() $\mathbf {I}$
to
$\mathbf {I}$
to
![]() $\mathbf {I}$
(see Figure 5) are defined by
$\mathbf {I}$
(see Figure 5) are defined by

Figure 5 Graphs of
![]() $f_{-1}$
and
$f_{-1}$
and
![]() $f_1$
.
$f_1$
.
We want to show that, for every
![]() $n \in \mathbb {Z}$
, the random variable
$n \in \mathbb {Z}$
, the random variable
![]() $Y_n$
can be almost surely recovered from the knowledge of
$Y_n$
can be almost surely recovered from the knowledge of
![]() $(\eta _k)_{k \le n}$
. To do this, we introduce the random maps
$(\eta _k)_{k \le n}$
. To do this, we introduce the random maps
![]() $F_n := f_{\eta _n} \circ \cdots \circ f_{\eta _1}$
and the
$F_n := f_{\eta _n} \circ \cdots \circ f_{\eta _1}$
and the
![]() $\sigma $
-fields
$\sigma $
-fields
![]() $\mathcal {F}_n = \sigma (\eta _1,\ldots ,\eta _n)$
for
$\mathcal {F}_n = \sigma (\eta _1,\ldots ,\eta _n)$
for
![]() $n \ge 0$
. Let
$n \ge 0$
. Let
![]() ${B_\theta := [0,\theta [ \times [\theta ,1[ \cup [\theta ,1[ \times [0,\theta [}$
and let D be the diagonal of
${B_\theta := [0,\theta [ \times [\theta ,1[ \cup [\theta ,1[ \times [0,\theta [}$
and let D be the diagonal of
![]() $\mathbf {I}^2$
. The global strategy, based on a coupling argument is unchanged.
$\mathbf {I}^2$
. The global strategy, based on a coupling argument is unchanged.
-
(1) For every
 $(y,y') \in \mathbf {I}^2$
, the process
$(y,y') \in \mathbf {I}^2$
, the process
 $((F_n(y),F_n(y'))_{n \ge 0}$
is a Markov chain on
$((F_n(y),F_n(y'))_{n \ge 0}$
is a Markov chain on
 $\mathbf {I}^2$
in the filtration
$\mathbf {I}^2$
in the filtration
 $(\mathcal {F}_n)_{n \ge 0}$
, whose transition probabilities (see Figure 6) are given by
$(\mathcal {F}_n)_{n \ge 0}$
, whose transition probabilities (see Figure 6) are given by  $$ \begin{align*}K((y,y'),\cdot) = \tfrac{1}{2}(\delta_{(f_{-1}(y),f_{-1}(y'))} + \delta_{(f_1(y),f_1(y'))}).\end{align*} $$
$$ \begin{align*}K((y,y'),\cdot) = \tfrac{1}{2}(\delta_{(f_{-1}(y),f_{-1}(y'))} + \delta_{(f_1(y),f_1(y'))}).\end{align*} $$
-
(2) The process
 $(A_n)_{n \ge 0}$
, defined by
$(A_n)_{n \ge 0}$
, defined by  $$ \begin{align*}A_n := \sum_{k=0}^{n-1} {\mathbf 1}_{B_\theta} (F_k(y),F_k(y')),\end{align*} $$
$$ \begin{align*}A_n := \sum_{k=0}^{n-1} {\mathbf 1}_{B_\theta} (F_k(y),F_k(y')),\end{align*} $$
is predictable in the filtration
 $(\mathcal {F}_n)_{n \ge 0}$
.
$(\mathcal {F}_n)_{n \ge 0}$
. -
(3) Given
 $(y,y') \in \mathbf {I}^2$
, the process
$(y,y') \in \mathbf {I}^2$
, the process
 $(\overline {(F_n(y')-F_n(y)})_{n \ge 0}$
with values in
$(\overline {(F_n(y')-F_n(y)})_{n \ge 0}$
with values in
 $\mathbb {R}/\mathbb {Z}$
is still a time-changed symmetric random walk, making steps
$\mathbb {R}/\mathbb {Z}$
is still a time-changed symmetric random walk, making steps
 $\pm 2\overline {\theta }$
, with probability
$\pm 2\overline {\theta }$
, with probability
 $1/2$
each. More precisely, for every
$1/2$
each. More precisely, for every
 $n \ge 0$
,
$n \ge 0$
,  $$ \begin{align*}F_n(y')-F_n(y) \equiv y'-y + 2\theta W_{A_n} \,\mod\!\!\: 1,\end{align*} $$
$$ \begin{align*}F_n(y')-F_n(y) \equiv y'-y + 2\theta W_{A_n} \,\mod\!\!\: 1,\end{align*} $$
where
 $(W_a)_{a \ge 0}$
is a simple symmetric random walk on
$(W_a)_{a \ge 0}$
is a simple symmetric random walk on
 $\mathbb {Z}$
, independent of
$\mathbb {Z}$
, independent of
 $(A_n)_{n \ge 0}$
.
$(A_n)_{n \ge 0}$
. -
(4) The process
 $((F_n(y),F_n(y'))_{n \ge 0}$
visits
$((F_n(y),F_n(y'))_{n \ge 0}$
visits
 $B_\theta $
more and more rarely:
$B_\theta $
more and more rarely:
 $A_n/n \to 0$
almost surely as
$A_n/n \to 0$
almost surely as
 $n \to +\infty $
.
$n \to +\infty $
. -
(5) The final argument given in §1.4 (which uses that invariant probability measures for K are carried by
 $B_\theta ^c$
, and therefore by D) is unchanged.
$B_\theta ^c$
, and therefore by D) is unchanged.
Yet, the laws of the reaching times of the set
![]() $B_\theta $
from any point
$B_\theta $
from any point
![]() $(y,y') \in D^c$
are very different in our new situation, and this changes notably the proof of step 3. The main changes occur in Lemmas 12 and 16 which must be replaced by Lemmas 17 and 18 below. The purpose is the same, namely, exhibiting situations that occur sufficiently often where the process
$(y,y') \in D^c$
are very different in our new situation, and this changes notably the proof of step 3. The main changes occur in Lemmas 12 and 16 which must be replaced by Lemmas 17 and 18 below. The purpose is the same, namely, exhibiting situations that occur sufficiently often where the process
![]() $((F_n(y),F_n(y'))_{n \ge 0}$
spends a lot of time outside of
$((F_n(y),F_n(y'))_{n \ge 0}$
spends a lot of time outside of
![]() $B_\theta $
(and, therefore, close to the diagonal D), but the assumptions and the lower bounds for the reaching time of
$B_\theta $
(and, therefore, close to the diagonal D), but the assumptions and the lower bounds for the reaching time of
![]() $B_\theta $
are different.
$B_\theta $
are different.

Figure 6 Probability transitions from different points
![]() $(y,y')$
. The probability associated to each arrow is
$(y,y')$
. The probability associated to each arrow is
![]() $1/2$
. The set
$1/2$
. The set
![]() $B_\theta $
is the union of the shaded rectangles. When
$B_\theta $
is the union of the shaded rectangles. When
![]() $(y,y') \in B_\theta ^c$
, the same rotation
$(y,y') \in B_\theta ^c$
, the same rotation
![]() $T_{\pm \theta }$
is applied to both coordinates. When
$T_{\pm \theta }$
is applied to both coordinates. When
![]() $(y,y') \in B_\theta $
, rotation
$(y,y') \in B_\theta $
, rotation
![]() $T_\theta $
is applied to one coordinate, whereas rotation
$T_\theta $
is applied to one coordinate, whereas rotation
![]() $T_{-\theta }$
is applied to the other one.
$T_{-\theta }$
is applied to the other one.
For every
![]() $a \ge 0$
, we set
$a \ge 0$
, we set
![]() $N_a=\inf \{n \ge 0 : A_n \ge a\}$
and
$N_a=\inf \{n \ge 0 : A_n \ge a\}$
and
![]() $\Delta N_a = N_{a+1}-N_a$
. By construction, the random times
$\Delta N_a = N_{a+1}-N_a$
. By construction, the random times
![]() $(N_a-1)_{a \ge 1}$
are exactly the visit times of
$(N_a-1)_{a \ge 1}$
are exactly the visit times of
![]() $B_\theta $
by the process
$B_\theta $
by the process
![]() $((F_n(y),F_n(y'))_{n \ge 0}$
, so they are stopping times in the filtration
$((F_n(y),F_n(y'))_{n \ge 0}$
, so they are stopping times in the filtration
![]() $(\mathcal {F}_n)_{n \ge 0}$
.
$(\mathcal {F}_n)_{n \ge 0}$
.
We now relate the distribution of
![]() $N_2-N_1$
given
$N_2-N_1$
given
![]() $W_1=-1$
with the distribution of stopping times of the form
$W_1=-1$
with the distribution of stopping times of the form
![]() $\tau _{-1,b} := \inf \{n \ge 0 : W_n \in \{-1,b\}\}$
with
$\tau _{-1,b} := \inf \{n \ge 0 : W_n \in \{-1,b\}\}$
with
![]() $b \ge 0$
.
$b \ge 0$
.
Remember that
![]() $\ell _{-1} = 1$
,
$\ell _{-1} = 1$
,
![]() $\ell _0=\theta $
,
$\ell _0=\theta $
,
![]() $\ell _1 = 1 -\lfloor 1/\theta \rfloor \theta < \min (\theta ,1-2\theta )$
and
$\ell _1 = 1 -\lfloor 1/\theta \rfloor \theta < \min (\theta ,1-2\theta )$
and
![]() $q_1 = a_1 \ge 2$
, since we assumed that
$q_1 = a_1 \ge 2$
, since we assumed that
![]() $0<\theta <1/2$
. Hence, the condition
$0<\theta <1/2$
. Hence, the condition
![]() $\delta \in ~]0,\min (\theta ,1-2\theta )[$
below holds whenever
$\delta \in ~]0,\min (\theta ,1-2\theta )[$
below holds whenever
![]() $0<\delta <\ell _1$
.
$0<\delta <\ell _1$
.
Lemma 17. Let
![]() $(y,y') \in \mathbf {I}^2$
. Assume that
$(y,y') \in \mathbf {I}^2$
. Assume that
![]() $(y,y') \in B_\theta $
(so
$(y,y') \in B_\theta $
(so
![]() $N_1=1$
) and that
$N_1=1$
) and that
![]() ${y'=T_{2\theta +\delta }(y)}$
for some
${y'=T_{2\theta +\delta }(y)}$
for some
![]() $\delta \in ~]0,\min (\theta ,1-2\theta )[$
. Then we have the following.
$\delta \in ~]0,\min (\theta ,1-2\theta )[$
. Then we have the following.
-
(1)
 $(T_\theta (y),T_{-\theta }(y')) \notin B_\theta $
. Hence, on the event
$(T_\theta (y),T_{-\theta }(y')) \notin B_\theta $
. Hence, on the event
 $[W_1=-1]$
,
$[W_1=-1]$
,
 $(F_1(y),F_1(y')) \notin B_\theta $
.
$(F_1(y),F_1(y')) \notin B_\theta $
. -
(2) If
 $\ell _k \le \delta < \ell _{k-1}$
with
$\ell _k \le \delta < \ell _{k-1}$
with
 $k \ge 2$
, then, for every
$k \ge 2$
, then, for every
 $\unicode{x3bb}>0$
,
$\unicode{x3bb}>0$
,  $$ \begin{align*} \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{- \Delta N_1}}{1-(\cosh\unicode{x3bb})^{-1}} \bigg|W_1=-1 \bigg] &\ge \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{-1-\tau_{-1,q_k-2}}}{1-(\cosh\unicode{x3bb})^{-1}}\bigg]\\[5pt] &= \frac{\tanh ((({q_k-1})/{2}) \unicode{x3bb} )}{\tanh(\unicode{x3bb}/2)}. \end{align*} $$
$$ \begin{align*} \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{- \Delta N_1}}{1-(\cosh\unicode{x3bb})^{-1}} \bigg|W_1=-1 \bigg] &\ge \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{-1-\tau_{-1,q_k-2}}}{1-(\cosh\unicode{x3bb})^{-1}}\bigg]\\[5pt] &= \frac{\tanh ((({q_k-1})/{2}) \unicode{x3bb} )}{\tanh(\unicode{x3bb}/2)}. \end{align*} $$
Proof. By assumption, we have
![]() $(y,y') \in [0,\theta [ \times [\theta ,1[$
or
$(y,y') \in [0,\theta [ \times [\theta ,1[$
or
![]() $(y,y') \in [\theta ,1[ \times [0,\theta [$
. Since
$(y,y') \in [\theta ,1[ \times [0,\theta [$
. Since
![]() $y'=(y+2\theta +\delta ) \,\mod \!\!\: 1$
, we get (see Figure 7)
$y'=(y+2\theta +\delta ) \,\mod \!\!\: 1$
, we get (see Figure 7)
 $$ \begin{align*} \begin{cases} 0 \le y < \min(\theta,1-2\theta-\delta) \\ 2\theta+\delta \le y' < \min(3\theta+\delta,1) \end{cases} \text{ or}\quad \begin{cases} \max(\theta,1-2\theta-\delta) \le y < 1-\theta-\delta \\ \max(3\theta+\delta-1,0) \le y' < \theta. \end{cases}\end{align*} $$
$$ \begin{align*} \begin{cases} 0 \le y < \min(\theta,1-2\theta-\delta) \\ 2\theta+\delta \le y' < \min(3\theta+\delta,1) \end{cases} \text{ or}\quad \begin{cases} \max(\theta,1-2\theta-\delta) \le y < 1-\theta-\delta \\ \max(3\theta+\delta-1,0) \le y' < \theta. \end{cases}\end{align*} $$
Thus,
 $$ \begin{align*}\begin{cases} \theta \le T_\theta(y) < \min(2\theta,1-\theta-\delta) \\ \theta+\delta \le T_{-\theta}(y') < \min(2\theta+\delta,1-\theta) \end{cases} \text{ or}\quad \begin{cases} \max(2\theta,1-\theta-\delta) \le T_\theta(y) < 1-\delta \\ \max(2\theta+\delta,1-\theta) \le T_{-\theta}(y') < 1. \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} \theta \le T_\theta(y) < \min(2\theta,1-\theta-\delta) \\ \theta+\delta \le T_{-\theta}(y') < \min(2\theta+\delta,1-\theta) \end{cases} \text{ or}\quad \begin{cases} \max(2\theta,1-\theta-\delta) \le T_\theta(y) < 1-\delta \\ \max(2\theta+\delta,1-\theta) \le T_{-\theta}(y') < 1. \end{cases}\end{align*} $$
In both cases,
![]() $(T_\theta (y),T_{-\theta }(y')) \notin B_\theta $
. This shows item (1).
$(T_\theta (y),T_{-\theta }(y')) \notin B_\theta $
. This shows item (1).

Figure 7 Possible locations of
![]() $(y,y')$
and
$(y,y')$
and
![]() $(T_\theta (y),T_{-\theta }(y'))$
when
$(T_\theta (y),T_{-\theta }(y'))$
when
![]() $(y,y') \in B_\theta $
and
$(y,y') \in B_\theta $
and
![]() $y'=T_{2\theta +\delta }(y)$
with
$y'=T_{2\theta +\delta }(y)$
with
![]() $0<\delta <\min (\theta ,1-2\theta )$
, depending on whether
$0<\delta <\min (\theta ,1-2\theta )$
, depending on whether
![]() $3\theta +\delta \ge 1$
(left) or
$3\theta +\delta \ge 1$
(left) or
![]() $3\theta +\delta \le 1$
(right). Under these assumptions, the couple
$3\theta +\delta \le 1$
(right). Under these assumptions, the couple
![]() $(T_\theta (y),T_{-\theta }(y'))$
is not in
$(T_\theta (y),T_{-\theta }(y'))$
is not in
![]() $B_\theta $
.
$B_\theta $
.
Let us prove item (2). Let a (respectively, b) be the number of iterations of the Cartesian product map
![]() $T_{-\theta } \times T_{-\theta }$
(respectively,
$T_{-\theta } \times T_{-\theta }$
(respectively,
![]() $T_\theta \times T_\theta $
) necessary to reach
$T_\theta \times T_\theta $
) necessary to reach
![]() $B_\theta $
from
$B_\theta $
from
![]() $(T_\theta (y),T_{-\theta }(y'))$
. By item (1), we have
$(T_\theta (y),T_{-\theta }(y'))$
. By item (1), we have
![]() $a \ge 1$
and
$a \ge 1$
and
![]() $b \ge 1$
. But, we have also
$b \ge 1$
. But, we have also
Since
![]() $T_\theta ([1-\delta ,1[) = [\theta -\delta ,\theta [$
, Corollary 6 yields
$T_\theta ([1-\delta ,1[) = [\theta -\delta ,\theta [$
, Corollary 6 yields
![]() $a+b \ge q_k-1$
.
$a+b \ge q_k-1$
.
On the event
![]() $[W_1=-1]$
, the random variable
$[W_1=-1]$
, the random variable
![]() $\Delta N_1-1 = (N_2-1)-N_1$
is the hitting time of
$\Delta N_1-1 = (N_2-1)-N_1$
is the hitting time of
![]() $\{-a,b\}$
by
$\{-a,b\}$
by
![]() $(W_{1+n}-W_1)_{n \ge 1}$
. This process is independent of
$(W_{1+n}-W_1)_{n \ge 1}$
. This process is independent of
![]() $W_1$
and is a symmetric simple random walk, like W. Hence, the distribution of
$W_1$
and is a symmetric simple random walk, like W. Hence, the distribution of
![]() $\Delta N_1-1$
under
$\Delta N_1-1$
under
![]() $\mathbf {P}[\cdot |W_1=-1]$
is the distribution on
$\mathbf {P}[\cdot |W_1=-1]$
is the distribution on
![]() $\tau _{-a,b} := \inf \{n \ge : W_n \in \{-a,b\}\}$
under
$\tau _{-a,b} := \inf \{n \ge : W_n \in \{-a,b\}\}$
under
![]() $\mathbf {P}$
. Thus, the gambler’s ruin theorem (Proposition 14) yields, for every
$\mathbf {P}$
. Thus, the gambler’s ruin theorem (Proposition 14) yields, for every
![]() $\unicode{x3bb}>0$
,
$\unicode{x3bb}>0$
,
 $$ \begin{align*} \mathbf{E} [(\cosh\unicode{x3bb})^{-(\Delta N_1-1)} |W_1=-1 ] &= \mathbf{E} [(\cosh\unicode{x3bb})^{-\tau_{-a,b}}] \\ &= \frac{\cosh ((({-a+b})/{2})\unicode{x3bb} )} {\cosh ((({a+b})/{2})\unicode{x3bb} )} \\ &\le \frac{\cosh (((({a+b})/{2})-1)\unicode{x3bb} )} {\cosh ((({a+b})/{2})\unicode{x3bb} )} \\ &= \mathbf{E}[(\cosh\unicode{x3bb})^{-\tau_{-1,a+b-1}}] \\ &\le \mathbf{E}[(\cosh\unicode{x3bb})^{-\tau_{-1,q_k-2}}] \textrm { since } \tau_{-1,a+b-1} \ge \tau_{-1,q_k-2} \\ &= \frac{\cosh ((({q_k-3})/{2})\unicode{x3bb} )} {\cosh ((({q_k-1})/{2})\unicode{x3bb} )}. \end{align*} $$
$$ \begin{align*} \mathbf{E} [(\cosh\unicode{x3bb})^{-(\Delta N_1-1)} |W_1=-1 ] &= \mathbf{E} [(\cosh\unicode{x3bb})^{-\tau_{-a,b}}] \\ &= \frac{\cosh ((({-a+b})/{2})\unicode{x3bb} )} {\cosh ((({a+b})/{2})\unicode{x3bb} )} \\ &\le \frac{\cosh (((({a+b})/{2})-1)\unicode{x3bb} )} {\cosh ((({a+b})/{2})\unicode{x3bb} )} \\ &= \mathbf{E}[(\cosh\unicode{x3bb})^{-\tau_{-1,a+b-1}}] \\ &\le \mathbf{E}[(\cosh\unicode{x3bb})^{-\tau_{-1,q_k-2}}] \textrm { since } \tau_{-1,a+b-1} \ge \tau_{-1,q_k-2} \\ &= \frac{\cosh ((({q_k-3})/{2})\unicode{x3bb} )} {\cosh ((({q_k-1})/{2})\unicode{x3bb} )}. \end{align*} $$
Hence,
 $$ \begin{align*} \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{- \Delta N_1}}{1-(\cosh\unicode{x3bb})^{-1}} \bigg|W_1=-1 \bigg] &\ge \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{-1-\tau_{-1,q_k-2}}}{1-(\cosh\unicode{x3bb})^{-1}}\bigg] \\ &= \mathbf{E} \bigg[\frac{\cosh\unicode{x3bb}-(\cosh\unicode{x3bb})^{-\tau_{-1,q_k-2}}}{\cosh\unicode{x3bb}-1}\bigg] \\ &= \frac{\cosh\unicode{x3bb} \cosh((({q_k-1})/{2})\unicode{x3bb} ) - \cosh((({q_k-3})/{2}) \unicode{x3bb} )} {(\cosh\unicode{x3bb}-1)\cosh((({q_k-1})/{2})\unicode{x3bb} )} \\ &= \frac{\sinh\unicode{x3bb} \sinh((({q_k-1})/{2}) \unicode{x3bb} )} {2\sinh^2(\unicode{x3bb}/2))\cosh ((({q_k-1})/{2})\unicode{x3bb} )} \\ &= \frac{\tanh((({q_k-1})/{2}) \unicode{x3bb} )} {\tanh(\unicode{x3bb}/2)}. \end{align*} $$
$$ \begin{align*} \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{- \Delta N_1}}{1-(\cosh\unicode{x3bb})^{-1}} \bigg|W_1=-1 \bigg] &\ge \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{-1-\tau_{-1,q_k-2}}}{1-(\cosh\unicode{x3bb})^{-1}}\bigg] \\ &= \mathbf{E} \bigg[\frac{\cosh\unicode{x3bb}-(\cosh\unicode{x3bb})^{-\tau_{-1,q_k-2}}}{\cosh\unicode{x3bb}-1}\bigg] \\ &= \frac{\cosh\unicode{x3bb} \cosh((({q_k-1})/{2})\unicode{x3bb} ) - \cosh((({q_k-3})/{2}) \unicode{x3bb} )} {(\cosh\unicode{x3bb}-1)\cosh((({q_k-1})/{2})\unicode{x3bb} )} \\ &= \frac{\sinh\unicode{x3bb} \sinh((({q_k-1})/{2}) \unicode{x3bb} )} {2\sinh^2(\unicode{x3bb}/2))\cosh ((({q_k-1})/{2})\unicode{x3bb} )} \\ &= \frac{\tanh((({q_k-1})/{2}) \unicode{x3bb} )} {\tanh(\unicode{x3bb}/2)}. \end{align*} $$
Item (2) follows.
Now, let us explain how we use Lemma 17.
By symmetry, the roles of y and
![]() $y'$
can be switched provided the event
$y'$
can be switched provided the event
![]() $[W_1=-1]$
is replaced with the event
$[W_1=-1]$
is replaced with the event
![]() $[W_1=1]$
.
$[W_1=1]$
.
For every
![]() $a \ge 1$
, we introduce a sign
$a \ge 1$
, we introduce a sign
![]() $\varepsilon _a$
which indicates the shortest path in the circle
$\varepsilon _a$
which indicates the shortest path in the circle
![]() $\mathbb {R}/\mathbb {Z}$
to go from
$\mathbb {R}/\mathbb {Z}$
to go from
![]() $\overline {Y_{N_a}}$
to
$\overline {Y_{N_a}}$
to
![]() $\overline {Y^{\prime }_{N_a}}$
. More precisely, we set
$\overline {Y^{\prime }_{N_a}}$
. More precisely, we set
 $$ \begin{align*} \varepsilon_a=1 &\textrm{ if } Y^{\prime}_{N_a}-Y_{N_a} \in ~ ]0,1/2[ + \mathbb{Z}, \\ \varepsilon_a=-1 &\textrm{ if } Y^{\prime}_{N_a}-Y_{N_a} \in ~ ]1/2,1[ + \mathbb{Z}, \\ \varepsilon_a=0 & \textrm{ if } Y^{\prime}_{N_a}-Y_{N_a} \in ~(1/2)\mathbb{Z}. \end{align*} $$
$$ \begin{align*} \varepsilon_a=1 &\textrm{ if } Y^{\prime}_{N_a}-Y_{N_a} \in ~ ]0,1/2[ + \mathbb{Z}, \\ \varepsilon_a=-1 &\textrm{ if } Y^{\prime}_{N_a}-Y_{N_a} \in ~ ]1/2,1[ + \mathbb{Z}, \\ \varepsilon_a=0 & \textrm{ if } Y^{\prime}_{N_a}-Y_{N_a} \in ~(1/2)\mathbb{Z}. \end{align*} $$
Given
![]() $\unicode{x3bb}>0$
, call
$\unicode{x3bb}>0$
, call
![]() $h_\unicode{x3bb} $
the function from
$h_\unicode{x3bb} $
the function from
![]() $[0,1/2]$
to
$[0,1/2]$
to
![]() $[0,+\infty ]$
defined by
$[0,+\infty ]$
defined by
![]() $h_\unicode{x3bb} (0)=+\infty $
,
$h_\unicode{x3bb} (0)=+\infty $
,
![]() $h_\unicode{x3bb} (r) = 1$
if
$h_\unicode{x3bb} (r) = 1$
if
![]() $r \ge \ell _1$
and
$r \ge \ell _1$
and
As
![]() $\unicode{x3bb} \to 0+$
,
$\unicode{x3bb} \to 0+$
,
![]() $h_\unicode{x3bb} (r)$
increases to
$h_\unicode{x3bb} (r)$
increases to
![]() $h(r)$
, where
$h(r)$
, where
![]() $h(0)=+\infty $
,
$h(0)=+\infty $
,
![]() $h(r) = 1$
if
$h(r) = 1$
if
![]() $r \ge \ell _1$
and
$r \ge \ell _1$
and
![]() $h(r):= q_k-1$
whenever
$h(r):= q_k-1$
whenever
![]() $\ell _k \le r < \ell _{k-1}$
with
$\ell _k \le r < \ell _{k-1}$
with
![]() $k \ge 2$
. We see that the integral of h over
$k \ge 2$
. We see that the integral of h over
![]() $[0,1/2]$
is infinite in the same way as we did for the function g in Lemma 16.
$[0,1/2]$
is infinite in the same way as we did for the function g in Lemma 16.
Hence, the strong Markov property at time
![]() $N_a$
and Lemma 17 yield the next lemma, which replaces Lemma 16.
$N_a$
and Lemma 17 yield the next lemma, which replaces Lemma 16.
Lemma 18. For every
![]() $a \ge 1$
and
$a \ge 1$
and
![]() $\unicode{x3bb}>0$
,
$\unicode{x3bb}>0$
,
 $$ \begin{align*} \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{\Delta N_a}}{1-\cosh\unicode{x3bb}} \bigg|\mathcal{F}_{N_a} \bigg] &\ge h_\unicode{x3bb}(\|Y^{\prime}_{N_a}-Y_{N_a}\|) {\mathbf 1}_{[W_a-W_{a-1} =-\varepsilon_a]} \\ &\ge h_\unicode{x3bb}(\|Y^{\prime}_{N_a-1}-Y_{N_a-1}-2\theta\|) {\mathbf 1}_{[W_a-W_{a-1} =-\varepsilon_a]}. \end{align*} $$
$$ \begin{align*} \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{\Delta N_a}}{1-\cosh\unicode{x3bb}} \bigg|\mathcal{F}_{N_a} \bigg] &\ge h_\unicode{x3bb}(\|Y^{\prime}_{N_a}-Y_{N_a}\|) {\mathbf 1}_{[W_a-W_{a-1} =-\varepsilon_a]} \\ &\ge h_\unicode{x3bb}(\|Y^{\prime}_{N_a-1}-Y_{N_a-1}-2\theta\|) {\mathbf 1}_{[W_a-W_{a-1} =-\varepsilon_a]}. \end{align*} $$
Therefore,
 $$ \begin{align*} \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{\Delta N_a}}{1-\cosh\unicode{x3bb}} \bigg|\mathcal{F}_{N_a-1} \bigg] &\ge \frac{1}{2}h_\unicode{x3bb}(\|Y^{\prime}_{N_a-1}-Y_{N_a-1}-2\theta\|). \end{align*} $$
$$ \begin{align*} \mathbf{E} \bigg[\frac{1-(\cosh\unicode{x3bb})^{\Delta N_a}}{1-\cosh\unicode{x3bb}} \bigg|\mathcal{F}_{N_a-1} \bigg] &\ge \frac{1}{2}h_\unicode{x3bb}(\|Y^{\prime}_{N_a-1}-Y_{N_a-1}-2\theta\|). \end{align*} $$
We now use Lemma 18. The inequalities above may be false for
![]() $a=0$
, but this as no influence on the Cesàró limits below. Observing that, for every
$a=0$
, but this as no influence on the Cesàró limits below. Observing that, for every
![]() $\unicode{x3bb}>0$
,
$\unicode{x3bb}>0$
,
and applying Lemma 13, we get, almost surely,
 $$ \begin{align*} \liminf_{a \to +\infty} \frac{N_a}{a} &= \liminf_{a \to +\infty} \frac{1}{a} \sum_{b=0}^{a-1} \Delta N_b \\ &\ge \liminf_{a \to +\infty} \frac{1}{a} \sum_{b=0}^{a-1} \frac{1-(\cosh\unicode{x3bb})^{\Delta N_b}}{1-\cosh\unicode{x3bb}}\\ &= \liminf_{a \to +\infty} \frac{1}{a} \sum_{b=0}^{a-1} \mathbf{E}\bigg[\frac{1-(\cosh\unicode{x3bb})^{\Delta N_b}}{1-\cosh\unicode{x3bb}} \bigg|\mathcal{F}_{N_a-1} \bigg] \\ &\ge \liminf_{a \to +\infty} \frac{1}{a} \sum_{b=0}^{a-1} h_\unicode{x3bb}(\|y'-y + 2\theta W_{a-1} -2\theta\|). \end{align*} $$
$$ \begin{align*} \liminf_{a \to +\infty} \frac{N_a}{a} &= \liminf_{a \to +\infty} \frac{1}{a} \sum_{b=0}^{a-1} \Delta N_b \\ &\ge \liminf_{a \to +\infty} \frac{1}{a} \sum_{b=0}^{a-1} \frac{1-(\cosh\unicode{x3bb})^{\Delta N_b}}{1-\cosh\unicode{x3bb}}\\ &= \liminf_{a \to +\infty} \frac{1}{a} \sum_{b=0}^{a-1} \mathbf{E}\bigg[\frac{1-(\cosh\unicode{x3bb})^{\Delta N_b}}{1-\cosh\unicode{x3bb}} \bigg|\mathcal{F}_{N_a-1} \bigg] \\ &\ge \liminf_{a \to +\infty} \frac{1}{a} \sum_{b=0}^{a-1} h_\unicode{x3bb}(\|y'-y + 2\theta W_{a-1} -2\theta\|). \end{align*} $$
The function
![]() $x \mapsto h_\unicode{x3bb} (\|x + y'-y - 2\theta \|)$
can be written as the limit of an increasing sequence of non-negative continuous
$x \mapsto h_\unicode{x3bb} (\|x + y'-y - 2\theta \|)$
can be written as the limit of an increasing sequence of non-negative continuous
![]() $1$
-periodic functions. Applying Lemma 15 and Beppo Levi’s lemma yields, almost surely,
$1$
-periodic functions. Applying Lemma 15 and Beppo Levi’s lemma yields, almost surely,
 $$ \begin{align*} \liminf_{a \to +\infty} \frac{1}{a} \sum_{b=0}^{a-1} h_\unicode{x3bb}(\|y'-y + 2\theta W_{a-1} -2\theta\|) &\ge \int_0^1 h_\unicode{x3bb}(\|x + y'-y - 2\theta\|)\, \mathrm{d}x \\ &= 2\int_0^{1/2} h_\unicode{x3bb}(r)\, \mathrm{d}r.\end{align*} $$
$$ \begin{align*} \liminf_{a \to +\infty} \frac{1}{a} \sum_{b=0}^{a-1} h_\unicode{x3bb}(\|y'-y + 2\theta W_{a-1} -2\theta\|) &\ge \int_0^1 h_\unicode{x3bb}(\|x + y'-y - 2\theta\|)\, \mathrm{d}x \\ &= 2\int_0^{1/2} h_\unicode{x3bb}(r)\, \mathrm{d}r.\end{align*} $$
Hence,
 $$ \begin{align*} \liminf_{a \to +\infty} \frac{N_a}{a} \ge 2\int_0^{1/2} h_\unicode{x3bb}(r)\, \mathrm{d}r \quad \text{ almost surely}. \end{align*} $$
$$ \begin{align*} \liminf_{a \to +\infty} \frac{N_a}{a} \ge 2\int_0^{1/2} h_\unicode{x3bb}(r)\, \mathrm{d}r \quad \text{ almost surely}. \end{align*} $$
Letting
![]() $\unicode{x3bb} $
go to zero and applying Beppo Levi’s lemma again yields
$\unicode{x3bb} $
go to zero and applying Beppo Levi’s lemma again yields
We derive that
![]() $A_n/n \to 0$
almost surely in the same way as we did for
$A_n/n \to 0$
almost surely in the same way as we did for
![]() $[T_\theta ,\mathrm {Id}]$
.
$[T_\theta ,\mathrm {Id}]$
.
5 Related results and open questions
In this section, we consider related questions that are still open and a few variants of what we have done for
![]() $[T_\theta ,\mathrm {Id}]$
and
$[T_\theta ,\mathrm {Id}]$
and
![]() $[T_\theta ,T_\theta ^{-1}]$
.
$[T_\theta ,T_\theta ^{-1}]$
.
5.1 Almost sure continuity of the isomorphism and its inverse
We come back to the transformation
![]() $[T_\theta ,\mathrm {Id}]$
defined on
$[T_\theta ,\mathrm {Id}]$
defined on
![]() $X \times \mathbf {I}$
, where
$X \times \mathbf {I}$
, where
![]() $X = \{0,1\}^{\mathbb {Z}y_+}$
and
$X = \{0,1\}^{\mathbb {Z}y_+}$
and
![]() $\mathbf {I} = [0,1[$
. We endow X with the product topology,
$\mathbf {I} = [0,1[$
. We endow X with the product topology,
![]() $\mathbf {I}$
with the topology deriving from the metric defined by
$\mathbf {I}$
with the topology deriving from the metric defined by
![]() $d(y,y') := \|y'-y\|$
and
$d(y,y') := \|y'-y\|$
and
![]() $X \times \mathbf {I}$
with the product topology. Since the map
$X \times \mathbf {I}$
with the product topology. Since the map
![]() $T_\theta $
is continuous on
$T_\theta $
is continuous on
![]() $\mathbf {I}$
, the map
$\mathbf {I}$
, the map
![]() $[T_\theta ,\mathrm {Id}]$
is continuous on
$[T_\theta ,\mathrm {Id}]$
is continuous on
![]() $X \times \mathbf {I}$
.
$X \times \mathbf {I}$
.
The map
![]() $\alpha _\theta : X \times \mathbf {I} \to \{0,1\}$
associated to Parry’s partition
$\alpha _\theta : X \times \mathbf {I} \to \{0,1\}$
associated to Parry’s partition
![]() $\alpha _\theta := \{A_0^\theta ,A_1^\theta \}$
is continuous
$\alpha _\theta := \{A_0^\theta ,A_1^\theta \}$
is continuous
![]() $\mu \otimes \nu $
-almost everywhere since it is given by
$\mu \otimes \nu $
-almost everywhere since it is given by
 $$ \begin{align*} \alpha_\theta(x,y) = {\mathbf 1}_{A_1^\theta}(x,y) &= ( {\mathbf 1}_{[(1-x_0)\theta + x_0(1-\theta),1[}(y) ) \,\mod\!\!\: 2 \\ &= ( x_0+{\mathbf 1}_{[\theta,1[}(T_\theta^{x(0)}(y)) ) \,\mod\!\!\: 2. \end{align*} $$
$$ \begin{align*} \alpha_\theta(x,y) = {\mathbf 1}_{A_1^\theta}(x,y) &= ( {\mathbf 1}_{[(1-x_0)\theta + x_0(1-\theta),1[}(y) ) \,\mod\!\!\: 2 \\ &= ( x_0+{\mathbf 1}_{[\theta,1[}(T_\theta^{x(0)}(y)) ) \,\mod\!\!\: 2. \end{align*} $$
The ‘
![]() $\alpha _\theta $
-name’ map
$\alpha _\theta $
-name’ map
![]() $\Phi _\theta : X \times \mathbf {I} \to \mathbf {I}$
is given by
$\Phi _\theta : X \times \mathbf {I} \to \mathbf {I}$
is given by
Since
![]() $[T_\theta ,\mathrm {Id}]$
is continuous and preserves
$[T_\theta ,\mathrm {Id}]$
is continuous and preserves
![]() $\mu \otimes \nu $
, we deduce that
$\mu \otimes \nu $
, we deduce that
![]() $\Phi _\theta $
is continuous
$\Phi _\theta $
is continuous
![]() $\mu \otimes \nu $
-almost everywhere.
$\mu \otimes \nu $
-almost everywhere.
We have proved that the partition
![]() $\alpha _\theta $
is an independent generator, so
$\alpha _\theta $
is an independent generator, so
![]() $\Phi _\theta $
is an isomorphism transforming the dynamical system
$\Phi _\theta $
is an isomorphism transforming the dynamical system
![]() $(X \times [0,1[,\mathcal {B}(X) \otimes \mathcal {P}([0,1[),\mu \otimes \nu ,[T_\theta ,\mathrm {Id}])$
into
$(X \times [0,1[,\mathcal {B}(X) \otimes \mathcal {P}([0,1[),\mu \otimes \nu ,[T_\theta ,\mathrm {Id}])$
into
![]() $(X,\mathcal {B}(X),\mu ,S)$
. Thouvenot asked me whether or not
$(X,\mathcal {B}(X),\mu ,S)$
. Thouvenot asked me whether or not
![]() $\Phi _\theta ^{-1}$
is continuous
$\Phi _\theta ^{-1}$
is continuous
![]() $\mu $
-almost everywhere. Answering this question is difficult since we do not have simple formulas to recover
$\mu $
-almost everywhere. Answering this question is difficult since we do not have simple formulas to recover
![]() $(x,y) \in X \times \mathbf {I}$
from
$(x,y) \in X \times \mathbf {I}$
from
![]() $\Phi _\theta (x,y)$
.
$\Phi _\theta (x,y)$
.
Once again, we reformulate our problem in probabilistic terms. Remember that
We know that
![]() $Y_0$
is almost surely a function of
$Y_0$
is almost surely a function of
![]() $(\eta _{-i})_{i \ge 0}$
. To prove that
$(\eta _{-i})_{i \ge 0}$
. To prove that
![]() $\Phi _\theta ^{-1}$
is continuous
$\Phi _\theta ^{-1}$
is continuous
![]() $\mu $
-almost everywhere, we just have to prove that this function is almost surely continuous, thanks to the recursion relations
$\mu $
-almost everywhere, we just have to prove that this function is almost surely continuous, thanks to the recursion relations
 $$ \begin{align*} \xi_{-i} &= ( \eta_{-i} + {\mathbf 1}_{[\theta,1[}(Y_{{-i}-1}) ) \,\mod\!\!\: 2 \\ &= ( \eta_{-i} + {\mathbf 1}_{[\theta,1[}(T_\theta^{\xi_{-i}+\cdots+\xi_0}(Y_0)) ) \,\mod\!\!\: 2. \end{align*} $$
$$ \begin{align*} \xi_{-i} &= ( \eta_{-i} + {\mathbf 1}_{[\theta,1[}(Y_{{-i}-1}) ) \,\mod\!\!\: 2 \\ &= ( \eta_{-i} + {\mathbf 1}_{[\theta,1[}(T_\theta^{\xi_{-i}+\cdots+\xi_0}(Y_0)) ) \,\mod\!\!\: 2. \end{align*} $$
For every
![]() $n \ge 0$
, we know that
$n \ge 0$
, we know that
that
![]() $(\eta _0,\ldots ,\eta _{-n+1})$
is independent of
$(\eta _0,\ldots ,\eta _{-n+1})$
is independent of
![]() $\mathcal {F}^{\xi ,Y}_{-n}$
and therefore of
$\mathcal {F}^{\xi ,Y}_{-n}$
and therefore of
![]() $Y_{-n}$
, and
$Y_{-n}$
, and
![]() $Y_{-n}$
is uniform on
$Y_{-n}$
is uniform on
![]() $\mathbf {I}$
.
$\mathbf {I}$
.
Given
![]() $n \ge 0$
, the random map
$n \ge 0$
, the random map
![]() $P_n = f_{\eta _0} \circ \cdots \circ f_{\eta _{-n+1}}$
has the same law as
$P_n = f_{\eta _0} \circ \cdots \circ f_{\eta _{-n+1}}$
has the same law as
![]() ${F_n = f_{\eta _n} \circ \cdots \circ f_{\eta _1}}$
. Yet, there is a great difference between the processes
${F_n = f_{\eta _n} \circ \cdots \circ f_{\eta _1}}$
. Yet, there is a great difference between the processes
![]() $(P_n)_{n \ge 0}$
and
$(P_n)_{n \ge 0}$
and
![]() $(F_n)_{n \ge 0}$
. When we couple in the past, the range
$(F_n)_{n \ge 0}$
. When we couple in the past, the range
![]() $P_n(\mathbf {I})$
can only decrease or stay equal as n increases. But when we couple in the future, no such inclusion holds. We only know that the Lebesgue measures
$P_n(\mathbf {I})$
can only decrease or stay equal as n increases. But when we couple in the future, no such inclusion holds. We only know that the Lebesgue measures
![]() $|F_n(\mathbf {I})|$
can only decrease or stay unchanged, since, for every
$|F_n(\mathbf {I})|$
can only decrease or stay unchanged, since, for every
![]() $n \ge 0$
, the set
$n \ge 0$
, the set
![]() $F_{n+1}(\mathbf {I})$
is the image of
$F_{n+1}(\mathbf {I})$
is the image of
![]() $F_n(\mathbf {I})$
by the random piecewise translation
$F_n(\mathbf {I})$
by the random piecewise translation
![]() $f_{\eta _{n+1}}$
.
$f_{\eta _{n+1}}$
.
Moreover, we have the following result.
Proposition 19. As n goes to infinity,
![]() $|F_n(\mathbf {I})|$
goes to zero almost surely.
$|F_n(\mathbf {I})|$
goes to zero almost surely.
Proof. For every
![]() $n \ge 0$
, consider the random set
$n \ge 0$
, consider the random set
![]() $E_n := \{y \in \mathbf {I} : F_n(T_{\theta }(y)) \ne F_n(y)\}$
. Then
$E_n := \{y \in \mathbf {I} : F_n(T_{\theta }(y)) \ne F_n(y)\}$
. Then
![]() $E_{n+1} \subset E_n$
, since
$E_{n+1} \subset E_n$
, since
![]() $F_{n+1} = f_{\eta _{n+1}} \circ E_n$
. Using that the random maps
$F_{n+1} = f_{\eta _{n+1}} \circ E_n$
. Using that the random maps
![]() $F_n$
are piecewise translations on
$F_n$
are piecewise translations on
![]() $\mathbf {I}$
, one checks that, for every
$\mathbf {I}$
, one checks that, for every
![]() $n \ge 0$
,
$n \ge 0$
,
![]() $F_n(\mathbf {I}) = F_n(E_n)$
so
$F_n(\mathbf {I}) = F_n(E_n)$
so
![]() $|F_n(\mathbf {I})| = |F_n(E_n)| \le |E_n|$
. Hence, it suffices to show that
$|F_n(\mathbf {I})| = |F_n(E_n)| \le |E_n|$
. Hence, it suffices to show that
![]() $|E_n|$
goes to zero in
$|E_n|$
goes to zero in
![]() $L^1(\mathbf {P})$
as n goes to infinity. By Fubini’s theorem and the Lebesgue dominated convergence theorem, one only needs to check that, for each
$L^1(\mathbf {P})$
as n goes to infinity. By Fubini’s theorem and the Lebesgue dominated convergence theorem, one only needs to check that, for each
![]() $y \in \mathbf {I}$
,
$y \in \mathbf {I}$
,
![]() $\mathbf {P}[y \in E_n] \to 0$
as
$\mathbf {P}[y \in E_n] \to 0$
as
![]() $n \to +\infty $
. This follows from Lemma 10, which shows that
$n \to +\infty $
. This follows from Lemma 10, which shows that
![]() $(F_n(T_\theta (y))-F_n(y))_{n \ge 0}$
is—modulo
$(F_n(T_\theta (y))-F_n(y))_{n \ge 0}$
is—modulo
![]() $1$
—a time-changed simple symmetric random walk on
$1$
—a time-changed simple symmetric random walk on
![]() $\theta \mathbb {Z}$
, with steps
$\theta \mathbb {Z}$
, with steps
![]() $\pm \theta $
, starting at
$\pm \theta $
, starting at
![]() $\theta $
and stopped when it hits zero.
$\theta $
and stopped when it hits zero.
This convergence is quite slow. In an online version of the paper, we establish that
![]() $\mathbf {E}[|F_n(\mathbf {I})|] \le \mathbf {E}[|E_n|] \le 2/q_k$
whenever
$\mathbf {E}[|F_n(\mathbf {I})|] \le \mathbf {E}[|E_n|] \le 2/q_k$
whenever
![]() $n \ge 2(q_k+q_{k-1})q_k^2$
. Since, for each
$n \ge 2(q_k+q_{k-1})q_k^2$
. Since, for each
![]() $n \ge 0$
, the random variables
$n \ge 0$
, the random variables
![]() $|P_n(\mathbf {I})|$
and
$|P_n(\mathbf {I})|$
and
![]() $|F_n(\mathbf {I})|$
have the same distribution, and since the sequence
$|F_n(\mathbf {I})|$
have the same distribution, and since the sequence
![]() $(P_n(\mathbf {I}))_{n \ge 0}$
is non-decreasing, we deduce that
$(P_n(\mathbf {I}))_{n \ge 0}$
is non-decreasing, we deduce that
![]() $|P_n(\mathbf {I})|$
also goes to zero almost surely as n goes to infinity. These facts and simulations (see Figure 8) lead us to formulate the following conjecture.
$|P_n(\mathbf {I})|$
also goes to zero almost surely as n goes to infinity. These facts and simulations (see Figure 8) lead us to formulate the following conjecture.

Figure 8 Five simulations showing the evolution of the length of the smallest interval of
![]() $\mathbf {I}$
(viewed as the circle
$\mathbf {I}$
(viewed as the circle
![]() $\mathbb {R}/\mathbb {Z}$
) containing
$\mathbb {R}/\mathbb {Z}$
) containing
![]() $P_n(\mathbf {I})$
, for
$P_n(\mathbf {I})$
, for
![]() $1 \le n \le 3000$
, when
$1 \le n \le 3000$
, when
![]() $\theta = (\sqrt {5}-1)/2$
.
$\theta = (\sqrt {5}-1)/2$
.
Conjecture 20. The diameter of
![]() $P_n(\mathbf {I})$
(for the distance d) goes almost surely to zero as n goes to infinity.
$P_n(\mathbf {I})$
(for the distance d) goes almost surely to zero as n goes to infinity.
Actually, we expect a still slower convergence. Observe that the conclusion will be false if we replace
![]() $P_n(\mathbf {I})$
by
$P_n(\mathbf {I})$
by
![]() $F_n(\mathbf {I})$
.
$F_n(\mathbf {I})$
.
If Conjecture 20 is true, this gives a positive answer to Thouvenot’s question. Indeed, given
![]() $\delta \in ~]0,1/2[$
, we can find almost surely an integer
$\delta \in ~]0,1/2[$
, we can find almost surely an integer
![]() $N \ge 1$
such that the diameter of
$N \ge 1$
such that the diameter of
![]() $P_n(\mathbf {I})$
is at most
$P_n(\mathbf {I})$
is at most
![]() $\delta $
. Then, the knowledge of
$\delta $
. Then, the knowledge of
![]() $\eta _0,\ldots ,\eta _{-N+1}$
only is sufficient to provide a random variable
$\eta _0,\ldots ,\eta _{-N+1}$
only is sufficient to provide a random variable
![]() $\tilde {Y}_0$
such that
$\tilde {Y}_0$
such that
![]() $\|Y_0 - \tilde {Y}_0\| \le \delta $
. Hence,
$\|Y_0 - \tilde {Y}_0\| \le \delta $
. Hence,
![]() $Y_0$
can be recovered with probability
$Y_0$
can be recovered with probability
![]() $1$
as an almost everywhere continuous function of
$1$
as an almost everywhere continuous function of
![]() $(\eta _{-i})_{i \ge 0}$
.
$(\eta _{-i})_{i \ge 0}$
.
Yet, proving this conjecture requires new ideas and looks difficult.
5.2 Changing the partition
To define the random sequence
![]() $(\eta _n)_{n \in \mathbb {Z}}$
, we split the interval
$(\eta _n)_{n \in \mathbb {Z}}$
, we split the interval
![]() $\mathbf {I} = [0,1[$
at
$\mathbf {I} = [0,1[$
at
![]() $\theta $
. An advantage of the (non-trivial) partition
$\theta $
. An advantage of the (non-trivial) partition
![]() $\iota = \{[0,\theta [,[\theta ,1[\}$
is that, for every
$\iota = \{[0,\theta [,[\theta ,1[\}$
is that, for every
![]() $n \ge 0$
, the partition
$n \ge 0$
, the partition
 $$ \begin{align*}\bigvee_{k=0}^n T_\theta^k\iota\end{align*} $$
$$ \begin{align*}\bigvee_{k=0}^n T_\theta^k\iota\end{align*} $$
comprises only
![]() $n+1$
intervals given by the subdivision
$n+1$
intervals given by the subdivision
![]() $((k\theta ) \,\mod \!\!\: 1)_{0 \le k \le n}$
, which is the least number possible. This facilitates the study of the random maps
$((k\theta ) \,\mod \!\!\: 1)_{0 \le k \le n}$
, which is the least number possible. This facilitates the study of the random maps
![]() $F_n = f_{\eta _n} \circ \cdots \circ f_{\eta _1}$
.
$F_n = f_{\eta _n} \circ \cdots \circ f_{\eta _1}$
.
Yet, if the definition of the sequence
![]() $(\eta _n)_{n \in \mathbb {Z}}$
is modified only by a modification of the splitting point—
$(\eta _n)_{n \in \mathbb {Z}}$
is modified only by a modification of the splitting point—
![]() $\alpha $
instead of
$\alpha $
instead of
![]() $\theta $
, say—a large part of our preceding analysis remains true, namely, Lemma 10 and its variant for
$\theta $
, say—a large part of our preceding analysis remains true, namely, Lemma 10 and its variant for
![]() $[T_\theta ,T_\theta ^{-1}]$
. Yet, the set
$[T_\theta ,T_\theta ^{-1}]$
. Yet, the set
![]() $B_\theta $
must be replaced by
$B_\theta $
must be replaced by
![]() $B_\alpha $
, and estimating the reaching time of
$B_\alpha $
, and estimating the reaching time of
![]() $B_\alpha $
from any point in
$B_\alpha $
from any point in
![]() $\mathbf {I}^2$
is less simple.
$\mathbf {I}^2$
is less simple.
A remarkable phenomenon occurs when we study
![]() $[T_\theta ,T_\theta ^{-1}]$
and split
$[T_\theta ,T_\theta ^{-1}]$
and split
![]() $\mathbf {I}$
at
$\mathbf {I}$
at
![]() $1/2$
: namely, when we set
$1/2$
: namely, when we set
Indeed, replacing the Markov chain
![]() $((\xi _n,Y_n))_{n \in \mathbb {Z}}$
by
$((\xi _n,Y_n))_{n \in \mathbb {Z}}$
by
![]() $((-\xi _n,(1-Y_n) \,\mod \!\!\: 1)_{n \in \mathbb {Z}}$
preserves its law and modifies the sequence
$((-\xi _n,(1-Y_n) \,\mod \!\!\: 1)_{n \in \mathbb {Z}}$
preserves its law and modifies the sequence
![]() $(\eta _n)_{n \in \mathbb {Z}}$
only on a null set, namely, on the negligible event
$(\eta _n)_{n \in \mathbb {Z}}$
only on a null set, namely, on the negligible event
![]() $[\text {there exists } n \in \mathbb {N} : Y_n \in \{0,1/2\}]$
. Hence, the knowledge of
$[\text {there exists } n \in \mathbb {N} : Y_n \in \{0,1/2\}]$
. Hence, the knowledge of
![]() $(\eta _n)_{n \in \mathbb {Z}}$
is not sufficient to recover almost surely the Markov chain
$(\eta _n)_{n \in \mathbb {Z}}$
is not sufficient to recover almost surely the Markov chain
![]() $((\xi _n,Y_n))_{n \in \mathbb {Z}}$
. By symmetry, at least one bit of information is lost.
$((\xi _n,Y_n))_{n \in \mathbb {Z}}$
. By symmetry, at least one bit of information is lost.
We complete this observation with a coupling argument to prove that only one bit of information is lost. Given y and
![]() $y'$
in
$y'$
in
![]() $\mathbf {I}$
, look at the Markov chain
$\mathbf {I}$
, look at the Markov chain
![]() $((F_n(y),F_n(y'))_{n \ge 0}$
, where
$((F_n(y),F_n(y'))_{n \ge 0}$
, where
![]() $F_n = f_{\eta _n} \circ \cdots \circ f_{\eta _1}$
.
$F_n = f_{\eta _n} \circ \cdots \circ f_{\eta _1}$
.
-
• On the event
 $[(F_n(y),F_n(y')) \in B_{1/2}^c]$
, we have
$[(F_n(y),F_n(y')) \in B_{1/2}^c]$
, we have  $$ \begin{align*}\|F_{n+1}(y')-F_{n+1}(y)\| = \|F_n(y')-F_n(y)\| \le \|F_n(y')+F_n(y)\|.\end{align*} $$
$$ \begin{align*}\|F_{n+1}(y')-F_{n+1}(y)\| = \|F_n(y')-F_n(y)\| \le \|F_n(y')+F_n(y)\|.\end{align*} $$
-
• On the event
 $[(F_n(y),F_n(y')) \in B_{1/2}]$
, we have
$[(F_n(y),F_n(y')) \in B_{1/2}]$
, we have  $$ \begin{align*}\|F_{n+1}(y')+F_{n+1}(y)\| = \|F_n(y')+F_n(y)\| \le \|F_n(y')-F_n(y)\|.\end{align*} $$
$$ \begin{align*}\|F_{n+1}(y')+F_{n+1}(y)\| = \|F_n(y')+F_n(y)\| \le \|F_n(y')-F_n(y)\|.\end{align*} $$
As a result, the quantity
![]() $\min (\|F_n(y')+F_n(y)\|,\|F_n(y')-F_n(y)\|)$
can only decrease or stay unchanged, so it tends to zero since
$\min (\|F_n(y')+F_n(y)\|,\|F_n(y')-F_n(y)\|)$
can only decrease or stay unchanged, so it tends to zero since
![]() $\liminf _{n \to +\infty }\|F_n(y')-F_n(y)\| = 0$
.
$\liminf _{n \to +\infty }\|F_n(y')-F_n(y)\| = 0$
.
Therefore, if
![]() $Y' := (Y^{\prime }_n)_{n \in \mathbb {Z}}$
is a copy of
$Y' := (Y^{\prime }_n)_{n \in \mathbb {Z}}$
is a copy of
![]() $Y := (Y_n)_{n \in \mathbb {Z}y}$
such that Y and
$Y := (Y_n)_{n \in \mathbb {Z}y}$
such that Y and
![]() $Y'$
are independent and identically distributed conditionally on
$Y'$
are independent and identically distributed conditionally on
![]() $\eta := (\eta _n)_{n \in \mathbb {Z}}$
, the process
$\eta := (\eta _n)_{n \in \mathbb {Z}}$
, the process
![]() $((Y_n,Y^{\prime }_n))_{n \in \mathbb {Z}}$
thus obtained is a stationary Markov chain with transition kernel K, so it lives almost surely on
$((Y_n,Y^{\prime }_n))_{n \in \mathbb {Z}}$
thus obtained is a stationary Markov chain with transition kernel K, so it lives almost surely on
![]() $D \cup D'$
, where
$D \cup D'$
, where
![]() $D'$
is the anti-diagonal
$D'$
is the anti-diagonal
Moreover,
![]() $D'$
is an absorbing set, like D. Since
$D'$
is an absorbing set, like D. Since
we derive that the conditional law
![]() $\mathcal {L}(Y|\eta )$
is almost surely carried by two points, which gives the desired conclusion.
$\mathcal {L}(Y|\eta )$
is almost surely carried by two points, which gives the desired conclusion.
This symmetry is an exceptional case. Intuitively, we may expect that no information is lost in the other cases, namely, when the splitting point is different from
![]() $1/2$
, or when we work with
$1/2$
, or when we work with
![]() $[T_\theta ,\mathrm {Id}]$
.
$[T_\theta ,\mathrm {Id}]$
.
5.3 Working with more general skew products
So far, we have worked only with
![]() $[T_\theta ,\mathrm {Id}]$
and
$[T_\theta ,\mathrm {Id}]$
and
![]() $[T_\theta ,T_\theta ^{-1}]$
. A natural generalization of these two transformations is
$[T_\theta ,T_\theta ^{-1}]$
. A natural generalization of these two transformations is
![]() $[T_\alpha ,T_\beta ]$
, where
$[T_\alpha ,T_\beta ]$
, where
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are real numbers such that
$\beta $
are real numbers such that
![]() $\beta -\alpha $
is irrational. The map
$\beta -\alpha $
is irrational. The map
![]() $[T_\alpha ,T_\beta ]$
can be defined on the product
$[T_\alpha ,T_\beta ]$
can be defined on the product
![]() $\{\alpha ,\beta \}^{\mathbb {Z}_+} \times \mathbf {I}$
by
$\{\alpha ,\beta \}^{\mathbb {Z}_+} \times \mathbf {I}$
by
Let
![]() $(Y_n)_{n \in \mathbb {Z}}$
be a Markov chain
$(Y_n)_{n \in \mathbb {Z}}$
be a Markov chain
![]() $(Y_n)_{n \in \mathbb {Z}}$
governed by the recursion relation
$(Y_n)_{n \in \mathbb {Z}}$
governed by the recursion relation
Let
![]() $\theta = \beta -\alpha $
. Define
$\theta = \beta -\alpha $
. Define
![]() $f_0$
and
$f_0$
and
![]() $f_1$
from
$f_1$
from
![]() $\mathbf {I}$
to
$\mathbf {I}$
to
![]() $\mathbf {I}$
by
$\mathbf {I}$
by
The graphs of
![]() $f_0$
and
$f_0$
and
![]() $f_1$
are drawn in Figure 9. The recursion governing
$f_1$
are drawn in Figure 9. The recursion governing
![]() $(Y_n)_{n \in \mathbb{Z}}$
can be written
$(Y_n)_{n \in \mathbb{Z}}$
can be written
![]() $Y_n = f_{\eta_n}(Y_{n-1})$
by adapting the definition of
$Y_n = f_{\eta_n}(Y_{n-1})$
by adapting the definition of
![]() $(\eta_n)_{n \in \mathbb{Z}}$
accordingly.
$(\eta_n)_{n \in \mathbb{Z}}$
accordingly.

Figure 9 The modified maps
![]() $f_0$
and
$f_0$
and
![]() $f_1$
.
$f_1$
.
Once again, we study the Markov chain
![]() $((F_n(y),F_n(y')))_{n \ge 0}$
, where
$((F_n(y),F_n(y')))_{n \ge 0}$
, where
![]() $(F_n)_{n \ge 0}$
is the sequence of random maps defined by
$(F_n)_{n \ge 0}$
is the sequence of random maps defined by
![]() $F_n = f_{\eta _n} \circ \cdots \circ f_{\eta _1}$
. Given y and
$F_n = f_{\eta _n} \circ \cdots \circ f_{\eta _1}$
. Given y and
![]() $y'$
in
$y'$
in
![]() $\mathbf {I}$
, the difference
$\mathbf {I}$
, the difference
![]() $F_n(y')-F_n(y)$
is still (modulo 1)
$F_n(y')-F_n(y)$
is still (modulo 1)
![]() $\theta $
times a time-changed symmetric simple random walk on
$\theta $
times a time-changed symmetric simple random walk on
![]() $\mathbb {Z}y$
, where the time change is given by the past sojourn time in
$\mathbb {Z}y$
, where the time change is given by the past sojourn time in
![]() $B_\theta $
of the process
$B_\theta $
of the process
![]() $((F_n(y),F_n(y')))_{n \ge 0}$
.
$((F_n(y),F_n(y')))_{n \ge 0}$
.
But this time, when the Markov chain
![]() $((F_n(y),F_n(y')))_{n \ge 0}$
is in
$((F_n(y),F_n(y')))_{n \ge 0}$
is in
![]() $B_\theta ^c$
, the steps it makes are uniform on
$B_\theta ^c$
, the steps it makes are uniform on
![]() $\{(-\alpha ,-\alpha ),(-\beta ,-\beta )\}$
. In this general context, estimating the reaching time of
$\{(-\alpha ,-\alpha ),(-\beta ,-\beta )\}$
. In this general context, estimating the reaching time of
![]() $B_\theta $
from any point in
$B_\theta $
from any point in
![]() $\mathbf {I}^2$
is much harder.
$\mathbf {I}^2$
is much harder.
Acknowledegments
I thank Jean-Paul Thouvenot for drawing my attention on this question and Jean-Brossard for his careful reading and fruitful comments. I also thank Vincent Beffara for nice simulations, including Figure 8.