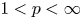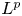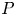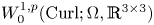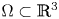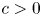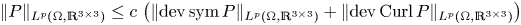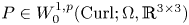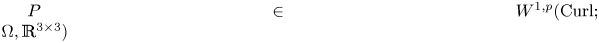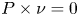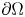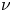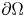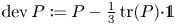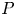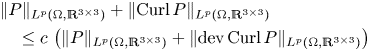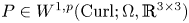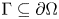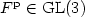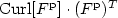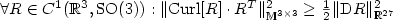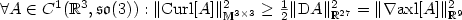For 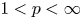 $1< p<\infty$ we prove an
$1< p<\infty$ we prove an 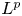 $L^{p}$-version of the generalized trace-free Korn inequality for incompatible tensor fields
$L^{p}$-version of the generalized trace-free Korn inequality for incompatible tensor fields 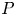 $P$ in
$P$ in 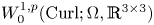 $W^{1,p}_0(\operatorname {Curl}; \Omega ,\mathbb {R}^{3\times 3})$. More precisely, let
$W^{1,p}_0(\operatorname {Curl}; \Omega ,\mathbb {R}^{3\times 3})$. More precisely, let 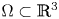 $\Omega \subset \mathbb {R}^{3}$ be a bounded Lipschitz domain. Then there exists a constant
$\Omega \subset \mathbb {R}^{3}$ be a bounded Lipschitz domain. Then there exists a constant 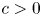 $c>0$ such that
$c>0$ such that
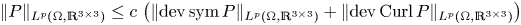 \[ \lVert{ P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})}\leq c\,\left(\lVert{\operatorname{dev} \operatorname{sym} P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})} + \lVert{ \operatorname{dev} \operatorname{Curl} P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})}\right) \]
\[ \lVert{ P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})}\leq c\,\left(\lVert{\operatorname{dev} \operatorname{sym} P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})} + \lVert{ \operatorname{dev} \operatorname{Curl} P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})}\right) \]
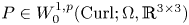 $P\in W^{1,p}_0(\operatorname {Curl}; \Omega ,\mathbb {R}^{3\times 3})$, i.e., for all
$P\in W^{1,p}_0(\operatorname {Curl}; \Omega ,\mathbb {R}^{3\times 3})$, i.e., for all 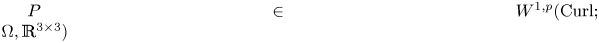 $P\in W^{1,p} (\operatorname {Curl}; \Omega ,\mathbb {R}^{3\times 3})$ with vanishing tangential trace
$P\in W^{1,p} (\operatorname {Curl}; \Omega ,\mathbb {R}^{3\times 3})$ with vanishing tangential trace 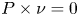 $P\times \nu =0$ on
$P\times \nu =0$ on 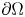 $\partial \Omega$ where
$\partial \Omega$ where 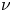 $\nu$ denotes the outward unit normal vector field to
$\nu$ denotes the outward unit normal vector field to 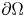 $\partial \Omega$ and
$\partial \Omega$ and 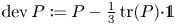 $\operatorname {dev} P : = P -\frac 13 \operatorname {tr}(P) {\cdot } {\mathbb {1}}$ denotes the deviatoric (trace-free) part of
$\operatorname {dev} P : = P -\frac 13 \operatorname {tr}(P) {\cdot } {\mathbb {1}}$ denotes the deviatoric (trace-free) part of 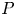 $P$. We also show the norm equivalence
$P$. We also show the norm equivalence
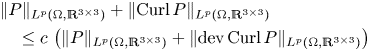 \begin{align*} &\lVert{ P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})}+\lVert{ \operatorname{Curl} P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})}\\ &\quad\leq c\,\left(\lVert{P}\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})} + \lVert{ \operatorname{dev} \operatorname{Curl} P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})}\right) \end{align*}
\begin{align*} &\lVert{ P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})}+\lVert{ \operatorname{Curl} P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})}\\ &\quad\leq c\,\left(\lVert{P}\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})} + \lVert{ \operatorname{dev} \operatorname{Curl} P }\rVert_{L^{p}(\Omega,\mathbb{R}^{3\times 3})}\right) \end{align*}
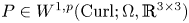 $P\in W^{1,p}(\operatorname {Curl}; \Omega ,\mathbb {R}^{3\times 3})$. These estimates also hold true for tensor fields with vanishing tangential trace only on a relatively open (non-empty) subset
$P\in W^{1,p}(\operatorname {Curl}; \Omega ,\mathbb {R}^{3\times 3})$. These estimates also hold true for tensor fields with vanishing tangential trace only on a relatively open (non-empty) subset 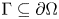 $\Gamma \subseteq \partial \Omega$ of the boundary.
$\Gamma \subseteq \partial \Omega$ of the boundary.