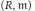1 results
On Set Theoretically and Cohomologically Complete Intersection Ideals
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 477-484
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
-
Let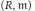
$\left( R,\,\mathfrak{m} \right)$ be a local ring and 
$\mathfrak{a}$ be an ideal of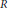 
$R$. The inequalities
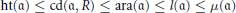$$\text{ht}\left( \mathfrak{a} \right)\,\le \,\text{cd}\left( \mathfrak{a},\,R \right)\,\le \,\text{ara}\left( \mathfrak{a} \right)\,\le \,l\left( \mathfrak{a} \right)\,\le \,\mu \left( \mathfrak{a} \right)$$are known. It is an interesting and long-standing problem to determine the cases giving equality. Thanks to the formal grade we give conditions in which the above inequalities become equalities.
