Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T06:27:31.032Z Has data issue: false hasContentIssue false
  • English
  • Français

On Set Theoretically and Cohomologically Complete Intersection Ideals

Published online by Cambridge University Press:  20 November 2018

Majid Eghbali
Majid Eghbali*
Affiliation:
School of Mathematics, Institute for Research in Fundamental Sciences (IPM), Tehran-Iran e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 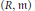$\left( R,\,\mathfrak{m} \right)$ be a local ring and $\mathfrak{a}$ be an ideal of 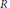$R$. The inequalities

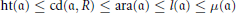$$\text{ht}\left( \mathfrak{a} \right)\,\le \,\text{cd}\left( \mathfrak{a},\,R \right)\,\le \,\text{ara}\left( \mathfrak{a} \right)\,\le \,l\left( \mathfrak{a} \right)\,\le \,\mu \left( \mathfrak{a} \right)$$

are known. It is an interesting and long-standing problem to determine the cases giving equality. Thanks to the formal grade we give conditions in which the above inequalities become equalities.

Keywords

13D4513C14set-theoretically and cohomologically complete intersection idealsanalytic spreadmonomialsformal gradedepth of powers of ideals
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 3 , 01 September 2014 , pp. 477 - 484
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Asgharzadeh, M. and Divaani-Aazar, K., Finiteness properties of formal local cohomology modules and Cohen-Macaulayness. Comm. Algebra 39 (2011), no. 3, 1082–1103. http://dx.doi.org/10.1080/00927871003610312 Google Scholar
[2] Barile, M., On the number of equations defining certain varieties. Manuscripta Math. 91 (1996), 483–494. http://dx.doi.org/10.1007/BF02567968 Google Scholar
[3] Barile, M., A note on monomial ideals. Arch. Math. 87 (2006), no. 6, 516–521. http://dx.doi.org/10.1007/s00013-006-1834-3 Google Scholar
[4] Brodmann, M., The asymptotic nature of the analytic spread. Math. Proc. Cambridge Philos. Soc. 86 (1979), no. 1, 35–39. http://dx.doi.org/10.1017/S030500410000061X Google Scholar
[5] Brodmann, M. P. and Sharp, R. Y., Local cohomology: an algebraic introduction with geometric applications. Cambridge Studies in Advanced Mathematics, 60, Cambridge University Press, Cambridge, 1998.Google Scholar
[6] Bruns, W. and Herzog, J., Cohen-Macaulay rings. Cambridge Studies in Advanced Mathematics, 39, Cambridge University Press, Cambridge, 1993.Google Scholar
[7] Burch, L., Codimension and analytic spread. Proc. Cambridge Philos. Soc. 72 (1972), 369–373. http://dx.doi.org/10.1017/S0305004100047198 Google Scholar
[8] Cowsik, R. C., Symbolic powers and numbers of defining equations. In: Algebra and its applications (New Delhi, 1981), Lecture Notes in Pure and Applied Math., 91, Dekker, New York, 1984, pp. 13–14.Google Scholar
[9] Cowsik, R. C. and Nori, M. V., On the fibers of blowing up. J. Indian Math. Soc. (N.S.) 40 (1976), no. 1–4, 217–222.Google Scholar
[10] Eghbali, M., On Artinianness of formal local cohomology, colocalization and coassociated primes. Math. Scand. 113 (2013), no. 1, 5–19.Google Scholar
[11] Eisenbud, D. and Huneke, C., Cohen-Macaulay Rees algebras and their specialization. J. Algebra 81 (1983), no. 1, 202–224. http://dx.doi.org/10.1016/0021-8693(83)90216-8 Google Scholar
[12] Hellus, M. and Schenzel, P., On cohomologically complete intersections. J. Algebra 320 (2008), no. 10, 3733–3748. http://dx.doi.org/10.1016/j.jalgebra.2008.09.006 Google Scholar
[13] Herzog, J., Takayama, Y., and Terai, N., On the radical of a monomial ideal. Arch. Math. 85 (2005), no. 5, 397–408. http://dx.doi.org/10.1007/s00013-005-1385-z Google Scholar
[14] Kimura, K., Terai, N., and Yoshida, K. I., Arithmetical rank of squarefree monomial ideals of small arithmetic degree. J. Algebraic Combin. 29 (2009), no. 3, 389–404. http://dx.doi.org/10.1007/s10801-008-0142-3 Google Scholar
[15] Lyubeznik, G., A survey of problems and results on the number of defining equations. In: Commutative algebra (Berkeley, CA, 1987), Math. Sci. Res. Inst. Publ., 15, Springer, New York, 1989, pp. 375–390.Google Scholar
[16] Lyubeznik, G., On the local cohomology modules Hia (R) for ideals a generated by monomials in an R-sequence. In: Complete intersections (Acireale, 1983), Lecture Notes in Math., 1092, Springer, Berlin, 1984.Google Scholar
[17] Peskine, C. and Szpiro, L., Dimension projective finie et cohomologie locale. Applications `a la d´emonstration de conjectures de M. Auslander, H. Bass et A. Grothendieck. Inst. Hautes Etudes Sci. Publ. Math. 42 (1973),47–119.Google Scholar
[18] Schenzel, P., On formal local cohomology and connectedness. J. Algebra 315 (2007), no. 2, 894–923. http://dx.doi.org/10.1016/j.jalgebra.2007.06.015 Google Scholar
[19] Schenzel, P. and Vogel, W., On set-theoretic intersections. J. Algebra 48 (1977), no. 2, 401–408. http://dx.doi.org/10.1016/0021-8693(77)90317-9 Google Scholar
[20] Singh, A. and Walter, U., Local cohomology and pure morphisms. Illinois J. Math. 51 (2007), no. 1, 287–298.Google Scholar
[21] Trung, N. V. and Ikeda, S., When is the Rees algebra Cohen-Macaulay? Comm. Algebra 17 (1989), no. 12, 2893–2922. http://dx.doi.org/10.1080/00927878908823885 Google Scholar
[22] Weibel, C. A., An introduction to homological algebra. Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, Cambridge, 1994.Google Scholar
[23] Yan, Z., An ´etale analog of the Goresky-Macpherson formula for subspace arrangements. J. Pure Appl. Algebra 146 (2000), no. 3, 305–318. http://dx.doi.org/10.1016/S0022-4049(98)00128-5 Google Scholar