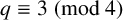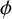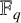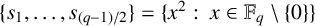2 results
A CONJECTURE OF ZHI-WEI SUN ON MATRICES CONCERNING MULTIPLICATIVE SUBGROUPS OF FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 September 2024, pp. 1-7
-
- Article
-
- You have access
- HTML
- Export citation
ON MATRICES ARISING IN FINITE FIELD HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 421-426
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation