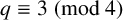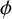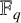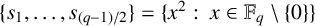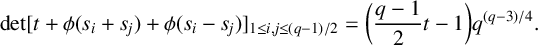1. Introduction
Let p be an odd prime. Research on determinants involving the Legendre symbol
$(\frac {\cdot }{p})$
can be traced back to Lehmer [Reference Lehmer4], Carlitz [Reference Carlitz1] and Chapman [Reference Chapman2]. For example, Carlitz [Reference Carlitz1, Theorem 4] studied the determinant
$$ \begin{align*} \det C(t):=\det\bigg[t+\bigg(\frac{i-j}{p}\bigg)\bigg]_{1\le i,j\le p-1} \end{align*} $$
and showed that
$$ \begin{align*}\det C(t)=(-1)^{{(p-1)}/{2}}p^{{(p-3)}/{2}}((p-1)t+(-1)^{{(p-1)}/{2}}).\end{align*} $$
Chapman [Reference Chapman2] investigated some variants of
$\det C(t)$
. For instance, Chapman considered
$$ \begin{align*}\det C_1(t):=\det \bigg[t+\bigg(\frac{i+j-1}{p}\bigg)\bigg]_{1\le i,j\le (p-1)/2}.\end{align*} $$
If we let
$\varepsilon _p>1$
and
$h_p$
be the fundamental unit and the class number of
$\mathbb {Q}(\sqrt {p})$
, respectively, then Chapman [Reference Chapman2] proved that
$$ \begin{align*}\det C_1(t)=\begin{cases} (-1)^{{(p-1)}/{4}}2^{{(p-1)}/{2}}(-a_pt+b_p) & \text{if}\ p\equiv 1\pmod4,\\ -2^{{(p-1)}/{2}}t & \text{if}\ p\equiv 3\pmod4, \end{cases}\end{align*} $$
where
$a_p,b_p\in \mathbb {Q}$
are defined by the equality
$$ \begin{align*}\varepsilon_p^{h_p}=a_p+b_p\sqrt{p}.\end{align*} $$
In 2019, Sun [Reference Sun5] initiated the study of determinants involving the Legendre symbol and binary quadratic forms. For example, Sun considered the determinant
$$ \begin{align*}\det S_p:=\det\bigg[\bigg(\frac{i^2+j^2}{p}\bigg)\bigg]_{1\le i,j\le (p-1)/2}.\end{align*} $$
Sun [Reference Sun5, Theorem 1.2] showed that
$-\det S_p$
is always a quadratic residue modulo p. See also [Reference Krachun, Petrov, Sun and Vsemirnov3, Reference Wu7] for recent work on this topic.
Recently, Sun [Reference Sun6] posed many interesting conjectures on determinants related to the Legendre symbol. We give one example.
Conjecture 1.1 (Sun; [Reference Sun6, Conjecture 1.1])
Let
$p\equiv 3\pmod 4$
be a prime. Then,
$$ \begin{align*}\det\bigg[t+\bigg(\frac{i^2+j^2}{p}\bigg)+\bigg(\frac{i^2-j^2}{p}\bigg)\bigg]_{1\le i,j\le (p-1)/2}=\bigg(\frac{p-1}{2}t-1\bigg)p^{{(p-3)}/{4}}.\end{align*} $$
Motivated by these results, we will study some determinants involving the quadratic multiplicative character of a finite field. We first introduce some notation.
Let
$q=p^s$
be an odd prime power with p prime and
$s\in \mathbb {Z}^+$
and let
$\mathbb {F}_q$
be the finite field of q elements. Let
$\mathbb {F}_q^{\times }$
be the cyclic group of all nonzero elements of
$\mathbb {F}_q$
. For any positive integer k which divides
$q-1$
, let
$$ \begin{align*}D_k:=\{a_1,a_2,\ldots,a_{(q-1)/k}\}=\{x^k:\ x\in\mathbb{F}_q^{\times}\}\end{align*} $$
be the subgroup of all nonzero kth powers in
$\mathbb {F}_q$
.
Let
$\widehat {\mathbb {F}_q^{\times }}$
be the cyclic group of all multiplicative characters of
$\mathbb {F}_q$
. Throughout this paper, for any
$\psi \in \widehat {\mathbb {F}_q^{\times }}$
, we extend
$\psi $
to
$\mathbb {F}_q$
by setting
$\psi (0)=0$
. Also, if
$2\nmid q$
, we use the symbol
$\phi $
to denote the unique quadratic multiplicative character of
$\mathbb {F}_q$
, that is,
$$ \begin{align*} \phi(x)=\begin{cases} 1 & \text{if}\ x\in D_2,\\ 0 & \text{if}\ x=0,\\ -1 & \text{otherwise.} \end{cases} \end{align*} $$
Inspired by the above results, we define the matrix
$A_k(t)$
by
$$ \begin{align*}A_k(t):=[t+\phi(a_i+a_j)+\phi(a_i-a_j)]_{1\le i,j\le (q-1)/k}.\end{align*} $$
The integers
$c_k$
and
$d_k$
, which are related to the number of
$\mathbb {F}_q$
-rational points of certain hyperelliptic curves over
$\mathbb {F}_q$
, are defined by
$$ \begin{align} |\{\infty\}\cup\{(x,y)\in\mathbb{F}_q\times\mathbb{F}_q:\ y^2=x^k+1\}|=q+1-c_k \end{align} $$
and
$$ \begin{align} |\{\infty\}\cup\{(x,y)\in\mathbb{F}_q\times\mathbb{F}_q:\ y^2=x^k-1\}|=q+1-d_k. \end{align} $$
Now we state the main results of this paper.
Theorem 1.2. Let
$q=p^s$
be an odd prime power with p prime and
$s\in \mathbb {Z}^+$
. Then, for any positive integer k which divides
$q-1$
, the following results hold.
-
(i) Suppose
$q\equiv 1\pmod {2k}$
. Then
$\det A_k(t)=0$
. In particular, if
$q\equiv 1\pmod 4$
, then
$\det A_2(t)=0$
. -
(ii) If
$q\equiv 3\pmod 4$
, then
$$ \begin{align*}\det A_2(t)=\bigg(\frac{q-1}{2}t-1\bigg)q^{{(q-3)}/{4}}.\end{align*} $$
-
(iii) Suppose
$q\equiv 1\pmod 4$
and
$q\not \equiv 1\pmod {2k}$
. Then there is an integer
$u_k$
such that
$$ \begin{align*}\det A_k(t)=\bigg(\frac{q-1}{k}t-\frac{1}{k}(c_k+d_k+2)\bigg)\cdot u_k^2.\end{align*} $$
Remark 1.3. (i) Theorem 1.2(i) generalises [Reference Sun6, Theorem 1.1] to an arbitrary finite field with odd characteristic. In the case where
$q=p$
is an odd prime, Theorem 1.2(ii) confirms Conjecture 1.1 posed by Zhi-Wei Sun.
(ii) For any k with
$3\le k<q-1$
,
$k\mid q-1$
and
$q-1\not \equiv 0\pmod {2k}$
, we can also obtain the explicit value of
$\det A_k(t)$
. However, finding a simple expression for
$\det A_k(t)$
seems very difficult.
We will prove our main results in Section 2.
2. Proof of Theorem 1.2
Throughout this section, we let
$\chi $
be a generator of
$\widehat {\mathbb {F}_q^{\times }}$
. Also, for any
$\chi ^i,\chi ^j\in \widehat {\mathbb {F}_q^{\times }}$
, the Jacobi sum of
$\chi ^i$
and
$\chi ^j$
is defined by
$$ \begin{align*}J(\chi^i,\chi^j)=\sum_{x\in\mathbb{F}_q}\chi^i(x)\chi^j(1-x).\end{align*} $$
We begin with a known result in linear algebra.
Lemma 2.1. Let n be a positive integer and let M be an
$n\times n$
complex matrix. Let
$\lambda _1,\ldots ,\lambda _n\in \mathbb {C}$
, and let
$\mathbf{v}_1,\ldots ,\mathbf{v}_n\in \mathbb {C}^n$
be column vectors. Suppose that
$$ \begin{align*}M\mathbf{v}_i=\lambda_i\mathbf{v}_i\end{align*} $$
for
$1\le i\le n$
and that the vectors
$\mathbf{v}_1,\ldots ,\mathbf{v}_n$
are linearly independent over
$\mathbb {C}$
. Then
$\lambda _1,\ldots ,\lambda _n$
are exactly all the eigenvalues of M (counting multiplicity).
Before the proof of our main results, we first introduce the definition of circulant matrices. Let R be a commutative ring and let
$b_0,b_1,\ldots ,b_{n-1}\in R$
. Then the circulant matrix of the tuple
$(b_0,b_1,\ldots ,b_{n-1})$
is defined by
$$ \begin{align*}C(b_0,b_1,\ldots,b_{n-1}):=[b_{i-j}]_{0\le i,j\le n-1},\end{align*} $$
where the indices are cyclic modulo n.
The second author [Reference Wu7, Lemma 3.4] proved the following result.
Lemma 2.2. Let
$n\ge 1$
be an odd integer. Let R be a commutative ring and let
$b_0,\ldots ,b_{n-1}\in R$
such that
$b_i=b_{n-i}$
for
$1\le i\le n-1$
. Then there is an element
$u\in R$
such that
$$ \begin{align*}\det C(b_0,b_1,\ldots,b_{n-1})=\bigg(\sum_{i=0}^{n-1}b_i\bigg)u^2.\end{align*} $$
Now we are in a position to prove our main results. For simplicity, we set
${n=(q-1)/k}$
.
Proof of Theorem 1.2
(i) Suppose
$q-1\equiv 0\pmod {2k}$
. Let
$\xi _{2k}\in \mathbb {F}_q$
be a primitive
$2k$
th root of unity. Then
$-1=\xi _{2k}^k\in D_k$
. Thus, for any j with
$1\le j\le n$
, there exists an integer
$j'$
with
$1\le j'\le n$
such that
$a_{j'}=-a_j$
and
$j\neq j'$
. This implies that the jth column of
$A_k(t)$
is the same as the
$j'$
th column of
$A_k(t)$
and hence
$\det A_k(t)=0$
.
(ii) Suppose now
$q-1\not \equiv 0\pmod {2k}$
. Then, clearly k is even. For any integers
$m,n$
with
$0\le m\le n-1$
and
$1\le i\le n$
,
$$ \begin{align*} \sum_{1\le j\le n} (\phi(a_i+a_j) +\phi(a_i-a_j))\chi^m(a_j) & =\sum_{1\le j\le n}\bigg(\phi\bigg(1+\frac{a_j}{a_i}\bigg)+\phi\bigg(1-\frac{a_j}{a_i}\bigg)\bigg)\ \chi^m\bigg(\frac{a_j}{a_i}\bigg)\ \chi^m(a_i)\\ & =\sum_{1\le j\le n}(\phi(1+a_j)+\phi(1-a_j))\chi^m(a_j)\chi^m(a_i). \end{align*} $$
Let
$$ \begin{align*}\mathbf{v}_m=(\chi^m(a_1),\chi^m(a_2),\ldots,\chi^m(a_n))^T \quad\text{and}\quad \lambda_m=\sum_{1\le j\le n}(\phi(1+a_j)+\phi(1-a_j))\chi^m(a_j).\end{align*} $$
By the above results,
$$ \begin{align*} A_k(0)\mathbf{v}_m=\lambda_m\mathbf{v}_m \quad\text{for } 0\le m\le n-1. \end{align*} $$
Since
$$ \begin{align*}\det [\chi^i(a_j)]_{0\le i\le n-1,1\le j\le n}=\prod_{1\le i<j\le n}(\chi(a_j)-\chi(a_i))\neq 0,\end{align*} $$
the vectors
$\mathbf{v}_0,\ldots ,\mathbf{v}_{n-1}$
are linearly independent over
$\mathbb {C}$
and hence by Lemma 2.1, the complex numbers
$\lambda _0,\ldots ,\lambda _{n-1}$
are exactly all the eigenvalues of
$A_k(0)$
.
Now let
$k=2$
. Then clearly
$q\equiv 3\pmod 4$
and n is odd in this case. We first evaluate
$\det A_2(0)$
. By the above,
$$ \begin{align} \det A_2(0)=\lambda_0\prod_{1\le m\le n-1}\lambda_m=\lambda_0\prod_{1\le m\le (n-1)/2}|\lambda_{2m}|^2. \end{align} $$
The last equality follows from
$\overline {\lambda _m}=\lambda _{n-m}$
for
$1\le m\le n-1$
. For
$\lambda _0$
,
$$ \begin{align} \lambda_0 =\sum_{1\le j\le n}(\phi(1+a_j)+\phi(1-a_j)) =\frac{1}{2}\sum_{x\in\mathbb{F}_q^{\times}}\phi(1+x^2)-\frac{1}{2}\sum_{x\in\mathbb{F}_q^{\times}}\phi(x^2-1) =-1. \end{align} $$
The last equality follows from
$$ \begin{align*}\sum_{x\in\mathbb{F}_q}\phi(x^2\pm 1)=-1.\end{align*} $$
For
$\lambda _{2m}$
with
$1\le m\le (n-1)/2$
, one can verify that
$$ \begin{align} \lambda_{2m} &=\sum_{1\le j\le n}(\phi(1+a_j)+\phi(1-a_j))\chi^{2m}(a_j) \notag \\ &=\frac{1}{2}\sum_{x\in\mathbb{F}_q}\phi(1+x^2)\chi^{2m}(x^2)+\frac{1}{2}\sum_{x\in\mathbb{F}_q}\phi(1-x^2)\chi^{2m}(-x^2) \notag \\ &=\sum_{x\in\mathbb{F}_q}\phi(1+x)\chi^{2m}(x) \notag \\ &=\sum_{x\in\mathbb{F}_q}\phi(1+x)\chi^{2m}(-x) =J(\phi,\chi^{2m}). \end{align} $$
Combining (2.2) and (2.3) with (2.1),
$$ \begin{align*}\det A_2(0)=-\prod_{1\le m\le (n-1)/2}|J(\phi,\chi^{2m})|^2=-q^{{(q-3)}/{4}}.\end{align*} $$
Now we turn to
$\det A_2(t)$
. By (2.2) for
$1\le j\le n$
,
$$ \begin{align*} \sum_{1\le i\le n}(t+\phi(a_i+a_j)+\phi(a_i-a_j)) & = nt+\sum_{1\le i\le n}(\phi(1+a_j/a_i)+\phi(1-a_j/a_i))\\ & = nt+\sum_{1\le i\le n}(\phi(1+a_i)+\phi(1-a_i))\\ & = nt-1. \end{align*} $$
This implies that
$(nt-1)\mid \det A_2(t)$
. Noting that
$\det A_2(t)\in \mathbb {Z}[t]$
with degree
$\le 1$
,
$$ \begin{align*}\det A_2(t)=-\det A_2(0)\cdot(nt-1)=q^{{(q-3)}/{4}}\bigg(\frac{q-1}{2}t-1\bigg).\end{align*} $$
(iii) Suppose
$q\equiv 1\pmod 4$
and
$q\not \equiv 1\pmod {2k}$
. Clearly,
$k\equiv 0\pmod 2$
in this case. Let
$g\in \mathbb {F}_q$
be a generator of the cyclic group
$\mathbb {F}_q^{\times }$
. Then one can verify that
$$ \begin{align*} \det A_k(t) &=\det[t+\phi(a_i+a_j)+\phi(a_i-a_j)]_{1\le i,j\le n}\\ &=\det [t+\phi(g^{k(i-j)}+1)+\phi(g^{k(i-j)}-1)]_{0\le i,j\le n-1}. \end{align*} $$
For
$0\le i\le n-1$
, let
$$ \begin{align*}b_i=t+\phi(g^{ki}+1)+\phi(g^{ki}-1).\end{align*} $$
Then one can easily verify that
$$ \begin{align*}\det A_k(t)=\det C(b_0,b_1,\ldots,b_{n-1})\end{align*} $$
and that
$b_i=b_{n-i}$
for
$1\le i\le n-1$
. Now applying Lemma 2.2, we see that there is an element
$u_k\in \mathbb {Z}[t]$
such that
$$ \begin{align*}\det A_k(t)=\bigg(\sum_{i=0}^{n-1}b_i\bigg)\cdot u_k^2.\end{align*} $$
One can verify that
$$ \begin{align*} \sum_{i=0}^{n-1}b_i &=nt+\sum_{1\le j\le n}(\phi(a_i+1)+\phi(a_i-1))\\ &=nt+\frac{1}{k}\sum_{x\in\mathbb{F}_q^{\times}}(\phi(x^k+1)+\phi(x^k-1))\\ &=nt-\frac{1}{k}(c_k+d_k+2), \end{align*} $$
where
$c_k$
and
$d_k$
are defined by (1.1) and (1.2), and the last equality follows from
$$ \begin{align*}\sum_{x\in\mathbb{F}_q^{\times}}\phi(x^k+1)=-c_k-1 \quad\text{and}\quad \sum_{x\in\mathbb{F}_q^{\times}}\phi(x^k-1)=-d_k-1.\end{align*} $$
As
$\det A_k(t)\in \mathbb {Z}[t]$
with degree
$\le 1$
, by the above, we see that
$u_k\in \mathbb {Z}$
. Hence,
$$ \begin{align*}\det A_k(t)=\bigg(\frac{q-1}{k}t-\frac{1}{k}(c_k+d_k+2)\bigg)\cdot u_k^2.\end{align*} $$
In view of the above, we have completed the proof of Theorem 1.2.
Acknowledgement
The authors would like to thank the referee for helpful comments.
