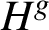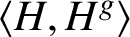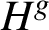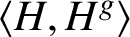A subgroup H of a group G is pronormal in G if each of its conjugates $H^g$ in G is conjugate to it in the subgroup $\langle H,H^g\rangle $ ; a group is prohamiltonian if all of its nonabelian subgroups are pronormal. The aim of the paper is to show that a locally soluble group of (regular) cardinality in which all proper uncountable subgroups are prohamiltonian is prohamiltonian. In order to obtain this result, it is proved that the class of prohamiltonian groups is detectable from the behaviour of countable subgroups. Examples are exhibited to show that there are uncountable prohamiltonian groups that do not behave very well. Finally, it is shown that prohamiltonicity can sometimes be detected through the analysis of the finite homomorphic images of a group.