Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T23:07:13.608Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUPS WITH MANY PRONORMAL SUBGROUPS

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  11 May 2021

MARIA FERRARA Open the ORCID record for MARIA FERRARA [Opens in a new window]  and
MARCO TROMBETTI Open the ORCID record for MARCO TROMBETTI [Opens in a new window]
MARIA FERRARA
Affiliation:
Dipartimento di Matematica e Fisica, Università degli Studi della Campania ‘Luigi Vanvitelli’, Viale Lincoln 5, Caserta, Italy e-mail: [email protected]
MARCO TROMBETTI*
Affiliation:
Dipartimento di Matematica e Applicazioni ‘Renato Caccioppoli’, Università degli Studi di Napoli Federico II, Complesso Universitario Monte S. Angelo, Via Cintia, Napoli, Italy
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A subgroup H of a group G is pronormal in G if each of its conjugates 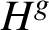$H^g$ in G is conjugate to it in the subgroup 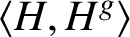$\langle H,H^g\rangle $ ; a group is prohamiltonian if all of its nonabelian subgroups are pronormal. The aim of the paper is to show that a locally soluble group of (regular) cardinality in which all proper uncountable subgroups are prohamiltonian is prohamiltonian. In order to obtain this result, it is proved that the class of prohamiltonian groups is detectable from the behaviour of countable subgroups. Examples are exhibited to show that there are uncountable prohamiltonian groups that do not behave very well. Finally, it is shown that prohamiltonicity can sometimes be detected through the analysis of the finite homomorphic images of a group.

Keywords

prohamiltonian grouppronormal subgroupcountably recognisable group class

MSC classification

Primary: 20E15: Chains and lattices of subgroups, subnormal subgroups
Secondary: 20E25: Local properties 20F16: Solvable groups, supersolvable groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 75 - 86
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Australian Mathematical Publishing Association Inc. 2021

Footnotes

The authors are supported by GNSAGA (INdAM) and are members of the non-profit association ‘Advances in Group Theory and Applications’ (www.advgrouptheory.com). The first author is supported by the project ‘Groups: overlappings between Algebra and Geometry, Logic and Mathematics Education’ (VALERE: VAnviteLli pEr la RicErca).

References

Baer, R., ‘Abzählbar erkennbare gruppentheoretische Eigenschaften’, Math. Z. 79 (1962), 344–363.CrossRefGoogle Scholar
Brescia, M., Ferrara, M. and Trombetti, M., ‘Groups whose subgroups are either abelian or pronormal’, Preprint.Google Scholar
Brescia, M. and Trombetti, M., ‘Locally finite simple groups whose non-abelian subgroups are pronormal’, Preprint.Google Scholar
De Falco, M., de Giovanni, F. and Musella, C., ‘Groups whose finite homomorphic images are metahamiltonian’, Comm. Algebra 37 (2009), 2468–2476.CrossRefGoogle Scholar
De Falco, M., de Giovanni, F. and Musella, C., ‘Metahamiltonian groups and related topics’, Int. J. Group Theory 2 (2013), 117–129.Google Scholar
de Giovanni, F. and Trombetti, M., ‘Uncountable groups with restrictions on subgroups of large cardinality’, J. Algebra 447 (2016), 383–396.CrossRefGoogle Scholar
de Giovanni, F. and Trombetti, M., ‘Nilpotency in uncountable groups’, J. Aust. Math. Soc. 103 (2017), 59–69.CrossRefGoogle Scholar
de Giovanni, F. and Trombetti, M., ‘The class of minimax groups is countably recognizable’, Monatsh. Math. 185 (2018), 81–86.CrossRefGoogle Scholar
de Giovanni, F. and Trombetti, M. ‘Groups with restrictions on proper uncountable subgroups’, Studia Sci. Math. Hungar. 56 (2019), 154–165.Google Scholar
de Giovanni, F. and Trombetti, M., ‘Pronormality in group theory’, Adv. Group Theory Appl. 9 (2020), 123–149.Google Scholar
de Giovanni, F. and Vincenzi, G., ‘Pronormality in infinite group theory’, Math. Proc. R. Ir. Acad. 100A (2000), 189–203.Google Scholar
Dixon, M. R., Evans, M. J. and Smith, H., ‘Groups with all proper subgroups soluble-by-finite rank’, J. Algebra 289 (2005), 135–147.CrossRefGoogle Scholar
Dixon, M. R., Evans, M. J. and Smith, H., ‘Some countably recognizable classes of groups’, J. Group Theory 10 (2007), 641–653.CrossRefGoogle Scholar
Ehrenfeucht, A. and Faber, V., ‘Do infinite nilpotent groups always have equipotent abelian subgroups?’, Indag. Math. 34 (1972), 202–209.CrossRefGoogle Scholar
Esposito, D., de Giovanni, F. and Trombetti, M., ‘Groups whose nonnormal subgroups are metahamiltonian’, Bull. Aust. Math. Soc. 102 (2020), 96–103.CrossRefGoogle Scholar
Ferrara, M. and Trombetti, M., ‘A countable-type theorem for uncountable groups’, Adv. Group Theory Appl. 3 (2017), 97–114.Google Scholar
Ferrara, M. and Trombetti, M., ‘Groups whose non-permutable subgroups are metaquasihamiltonian’, J. Group Theory 23 (2019), 513–529.CrossRefGoogle Scholar
Ferrara, M. and Trombetti, M., ‘A local study of group classes’, Note Mat. 40(2) (2020), 1–20.Google Scholar
Ferrara, M. and Trombetti, M., ‘Locally finite simple groups whose non-nilpotent subgroups are pronormal’, Preprint.Google Scholar
Kuzennyĭ, N. F. and Subbotin, I. Y., ‘Groups in which all of the subgroups are pronormal’, Ukrainian Math. J. 39(3) (1987), 251–254.CrossRefGoogle Scholar
Longobardi, P., Maj, M. and Smith, H., ‘A note on locally graded groups’, Rend. Semin. Mat. Univ. Padova 94 (1995), 275–277.Google Scholar
Ol’shanskii, A. Y., Geometry of Defining Relations in Groups (Kluwer Academic, Dordrecht, 1991).CrossRefGoogle Scholar
Oman, G., ‘Some results on Jónsson modules over a commutative ring’, Houston J. Math. 38 (2010), 3489–3498.Google Scholar
Peng, T. A., ‘Finite groups with pro-normal subgroups’, Proc. Amer. Math. Soc. 20 (1969), 232–234.CrossRefGoogle Scholar
Robinson, D. J. S., ‘A theorem on finitely generated hyperabelian groups’, Invent. Math. 10 (1970), 38–43.CrossRefGoogle Scholar
Robinson, D. J. S., Finiteness Conditions and Generalized Soluble Groups (Springer, Berlin, 1972).CrossRefGoogle Scholar
Robinson, D. J. S., ‘Groups whose homomorphic images have a transitive normality relation’, Trans. Amer. Math. Soc. 176 (1973), 181–213.CrossRefGoogle Scholar
Robinson, D. J. S., ‘Groups in which normality is a transitive relation’, Proc. Cambridge Philos. Soc. 60 (1964), 21–38.CrossRefGoogle Scholar
Rose, J. S., ‘Finite soluble groups with pronormal system normalizers’, Proc. Lond. Math. Soc. (3) 17 (1967), 447–469.CrossRefGoogle Scholar