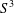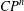1 results
THE MINIMAL
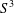 $S^{3}$ WITH CONSTANT SECTIONAL CURVATURE IN
$S^{3}$ WITH CONSTANT SECTIONAL CURVATURE IN 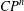 $\mathit{CP}^{n}$
$\mathit{CP}^{n}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 18 February 2015, pp. 63-75
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation