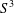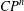Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hu, Zejun
Yin, Jiabin
and
Li, Zhenqi
2018.
Equivariant CR minimal immersions from $$S^3$$S3 into $$\mathbb CP^n$$CPn.
Annals of Global Analysis and Geometry,
Vol. 54,
Issue. 1,
p.
1.
Hu, Zejun
and
Yin, Jiabin
2019.
Equivariant Minimal Immersions from S3 into ℂP3.
Acta Mathematica Scientia,
Vol. 39,
Issue. 4,
p.
1065.