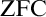1 results
AN AXIOMATIC APPROACH TO FORCING IN A GENERAL SETTING
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 04 April 2022, pp. 427-450
- Print publication:
- September 2022
-
- Article
- Export citation
-
The technique of forcing is almost ubiquitous in set theory, and it seems to be based on technicalities like the concepts of genericity, forcing names and their evaluations, and on the recursively defined forcing predicates, the definition of which is particularly intricate for the basic case of atomic first order formulas. In his [3], the first author has provided an axiomatic framework for set forcing over models of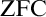
$\mathrm {ZFC}$
that is a collection of guiding principles for extensions over which one still has control from the ground model, and has shown that these axiomatics necessarily lead to the usual concepts of genericity and of forcing extensions, and also that one can infer from them the usual recursive definition of forcing predicates. In this paper, we present a more general such approach, covering both class forcing and set forcing, over various base theories, and we provide additional details regarding the formal setting that was outlined in [3].
