Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T01:56:42.194Z Has data issue: false hasContentIssue false
  • English
  • Français

AN AXIOMATIC APPROACH TO FORCING IN A GENERAL SETTING

Part of: Philosophical aspects of logic and foundations Set theory

Published online by Cambridge University Press:  04 April 2022

RODRIGO A. FREIRE  and
PETER HOLY
RODRIGO A. FREIRE
Affiliation:
DEPARTMENT OF PHILOSOPHY UNIVERSITY OF BRASÍLIABRASÍLIA, BRAZILE-mail: [email protected]
PETER HOLY
Affiliation:
UNIVERSITY OF UDINEUDINE, ITALYE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The technique of forcing is almost ubiquitous in set theory, and it seems to be based on technicalities like the concepts of genericity, forcing names and their evaluations, and on the recursively defined forcing predicates, the definition of which is particularly intricate for the basic case of atomic first order formulas. In his [3], the first author has provided an axiomatic framework for set forcing over models of 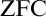$\mathrm {ZFC}$ that is a collection of guiding principles for extensions over which one still has control from the ground model, and has shown that these axiomatics necessarily lead to the usual concepts of genericity and of forcing extensions, and also that one can infer from them the usual recursive definition of forcing predicates. In this paper, we present a more general such approach, covering both class forcing and set forcing, over various base theories, and we provide additional details regarding the formal setting that was outlined in [3].

Keywords

forcingclass forcingaxiomatic framework for forcing

MSC classification

Primary: 03E40: Other aspects of forcing and Boolean-valued models
Secondary: 03E70: Nonclassical and second-order set theories 03A05: Philosophical and critical
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 28 , Issue 3 , September 2022 , pp. 427 - 450
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antos-Kuby, C., Class forcing in class theory , The Hyperuniverse Project and Maximality , Birkhäuser, Basel, 2018.CrossRefGoogle Scholar
Antos-Kuby, C., Sy David Friedman, and Victoria Gitman. Boolean-valued class forcing . Fundamenta Mathematicae , vol. 255 (2021), pp. 231–254.CrossRefGoogle Scholar
Freire, R., An axiomatic approach to forcing and generic extensions . Comptes Rendus Mathématique , vol. 358 (2020), no. 6, pp. 757–775.CrossRefGoogle Scholar
Friedman, S., Constructibility and class forcing , Handbook of Set Theory , vols. 1–3, Springer, Dordrecht, 2010, pp. 557–604.CrossRefGoogle Scholar
Friedman, S. D., Fine Structure and Class Forcing , De Gruyter Series in Logic and its Applications, 3, Walter de Gruyter, Berlin, 2000.CrossRefGoogle Scholar
Gitman, V., Hamkins, J., Holy, P., Schlicht, P., and Williams, K., The exact strength of the class forcing theorem . Journal of Symbolic Logic , vol. 85 (2020), no. 3, pp. 869–905.CrossRefGoogle Scholar
Holy, P., Krapf, R., Lücke, P., Njegomir, A., and Schlicht, P., Class forcing, the forcing theorem and Boolean completions . Journal of Symbolic Logic , vol. 81 (2016), no. 4, pp. 1500–1530.CrossRefGoogle Scholar
Holy, P., Krapf, R., and Schlicht, P., Characterizations of pretameness and the Ord-cc . Annals of Pure and Applied Logic , vol. 169 (2018), no. 8, pp. 775–802.CrossRefGoogle Scholar
Marek, W. and Mostowski, A., On extendability of models of ZF set theory to the models of Kelley–Morse theory of classes , Logic Conference, Kiel 1974, Lecture Notes in Mathematics, 499, Springer, Berlin, 1975, pp. 460–542.Google Scholar
Mathias, A., Provident sets and rudimentary set forcing. Fundamenta Mathematicae, vol. 230 (2015), no. 2, pp. 99–148.CrossRefGoogle Scholar