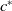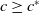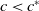1 results
Propagation dynamics of a mutualistic model of mistletoes and birds with nonlocal dispersal
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 04 December 2023, pp. 533-553
-
- Article
-
- You have access
- Open access
- HTML
- Export citation