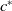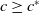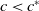1. Introduction
In ecology, mutual benefit between different populations is a common phenomenon. A special case is the relationship between mistletoes and birds. Mistletoes are typical aerial stem-parasites plants. Birds eat the fruit of mistletoes to obtain nutrients, energy and water. In turn, mistletoes receive directed movement of their propagules into safe germination sites [Reference Aukema and del Rio3]. To better understand the interaction between mistletoes and birds, Wang et al. [Reference Wang, Liu, Shi and Martinez26] proposed a reaction-diffusion model
 \begin{align} \begin{cases}\displaystyle u_t(t,x)= \displaystyle -d_mu+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\frac{u(t{-}\tau,y)}{u(t{-}\tau,y)+\omega }v(t{-}\tau, y)dy,\, t\ge 0, \, x\in \bar \Omega, \\[6pt] \displaystyle v_t(t,x)=D\Delta v+v(1-v)-\gamma \nabla (v\nabla u)\\[6pt] \, \, \, \, \, \, \, \, \, \, \, \, \, \, \displaystyle \quad +d\int _{\mathbb{R}}k(x-y)\frac{u(t,y)}{u(t,y)+\omega }v(t, y)dy, \, t\ge 0, \, x\in \bar \Omega,\\[6pt] \displaystyle (D\nabla v-\gamma v\nabla u)\cdot n(x)=0,\, t\ge 0, \, x\in \partial \Omega,\\[4pt] \displaystyle u(s,x)=u_0(s,x),\, v(s,x)=v_0(s,x),\, s\in [{-}\tau,0], \, x\in \Omega, \end{cases} \end{align}
\begin{align} \begin{cases}\displaystyle u_t(t,x)= \displaystyle -d_mu+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\frac{u(t{-}\tau,y)}{u(t{-}\tau,y)+\omega }v(t{-}\tau, y)dy,\, t\ge 0, \, x\in \bar \Omega, \\[6pt] \displaystyle v_t(t,x)=D\Delta v+v(1-v)-\gamma \nabla (v\nabla u)\\[6pt] \, \, \, \, \, \, \, \, \, \, \, \, \, \, \displaystyle \quad +d\int _{\mathbb{R}}k(x-y)\frac{u(t,y)}{u(t,y)+\omega }v(t, y)dy, \, t\ge 0, \, x\in \bar \Omega,\\[6pt] \displaystyle (D\nabla v-\gamma v\nabla u)\cdot n(x)=0,\, t\ge 0, \, x\in \partial \Omega,\\[4pt] \displaystyle u(s,x)=u_0(s,x),\, v(s,x)=v_0(s,x),\, s\in [{-}\tau,0], \, x\in \Omega, \end{cases} \end{align}
where the parameters
![]() $\alpha$
,
$\alpha$
,
![]() $d_i$
,
$d_i$
,
![]() $d_m$
,
$d_m$
,
![]() $D$
,
$D$
,
![]() $d$
,
$d$
,
![]() $\omega$
are positive constants, and the time delay
$\omega$
are positive constants, and the time delay
![]() $\tau$
is non-negative. In this model,
$\tau$
is non-negative. In this model,
![]() $u(t,x)$
and
$u(t,x)$
and
![]() $v(t,x)$
are the densities of mature mistletoes and birds at location
$v(t,x)$
are the densities of mature mistletoes and birds at location
![]() $x \in \Omega$
and time
$x \in \Omega$
and time
![]() $t$
, respectively,
$t$
, respectively,
![]() $\alpha$
is the hanging rate of mistletoe fruits to trees,
$\alpha$
is the hanging rate of mistletoe fruits to trees,
![]() $d_i$
and
$d_i$
and
![]() $d_m$
are the mortality rates of immature and mature mistletoes, respectively,
$d_m$
are the mortality rates of immature and mature mistletoes, respectively,
![]() $\tau$
is the maturation time of mistletoes,
$\tau$
is the maturation time of mistletoes,
![]() $D$
is the diffusion rate of birds,
$D$
is the diffusion rate of birds,
![]() $d$
is the conversion rate from mistletoe fruits into bird population. The term
$d$
is the conversion rate from mistletoe fruits into bird population. The term
![]() $v(1-v)$
models the logistic growth for bird population which measures the bird population growth due to other food resources besides mistletoes in the habitat,
$v(1-v)$
models the logistic growth for bird population which measures the bird population growth due to other food resources besides mistletoes in the habitat,
![]() $\gamma \nabla (v\nabla u)$
is a chemotactic term that models the effect that birds are attracted by trees with more mistletoes,
$\gamma \nabla (v\nabla u)$
is a chemotactic term that models the effect that birds are attracted by trees with more mistletoes,
![]() $\gamma$
is the chemotactic coefficient, and
$\gamma$
is the chemotactic coefficient, and
![]() $\omega$
is used to reflect the fact that birds may perch on other trees without mistletoes and structures irrelevant to the dynamic process of mistletoes. In [Reference Wang, Liu, Shi and Martinez26], the authors studied the spatial pattern formation under two different types of kernel functions
$\omega$
is used to reflect the fact that birds may perch on other trees without mistletoes and structures irrelevant to the dynamic process of mistletoes. In [Reference Wang, Liu, Shi and Martinez26], the authors studied the spatial pattern formation under two different types of kernel functions
![]() $k$
. When
$k$
. When
![]() $\Omega =\mathbb{R}$
and
$\Omega =\mathbb{R}$
and
![]() $\gamma =0$
, Wang et al. [Reference Wang, Liu, Shi and Martinez27] further investigated the existence of an asymptotic spreading speed and travelling wave solutions.
$\gamma =0$
, Wang et al. [Reference Wang, Liu, Shi and Martinez27] further investigated the existence of an asymptotic spreading speed and travelling wave solutions.
Note that in (1.1), the Fickian diffusion
![]() $D\Delta v$
is used to model the random movement of birds. It essentially is a local behaviour and hence maybe not accurate enough to describe the long-range effects of the dispersal of birds. In order to describe the dispersal of birds reasonably, Liang, Weng and Tian [Reference Liang, Weng and Tian19] introduced a nonlocal operator
$D\Delta v$
is used to model the random movement of birds. It essentially is a local behaviour and hence maybe not accurate enough to describe the long-range effects of the dispersal of birds. In order to describe the dispersal of birds reasonably, Liang, Weng and Tian [Reference Liang, Weng and Tian19] introduced a nonlocal operator
in (1.1) and presented the following nonlocal dispersal model of mistletoes and birds:
 \begin{align} \begin{cases}\displaystyle u_t(t,x)= \displaystyle -d_mu+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\frac{u(t{-}\tau,y)}{u(t{-}\tau,y)+\omega }v(t{-}\tau, y)dy, \\[6pt] \displaystyle v_t(t,x)=D(J*v-v)+v(1-v)+d\int _{\mathbb{R}}k(x-y)\frac{u(t,y)}{u(t,y)+\omega }v(t, y)dy, \end{cases} \end{align}
\begin{align} \begin{cases}\displaystyle u_t(t,x)= \displaystyle -d_mu+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\frac{u(t{-}\tau,y)}{u(t{-}\tau,y)+\omega }v(t{-}\tau, y)dy, \\[6pt] \displaystyle v_t(t,x)=D(J*v-v)+v(1-v)+d\int _{\mathbb{R}}k(x-y)\frac{u(t,y)}{u(t,y)+\omega }v(t, y)dy, \end{cases} \end{align}
where
![]() $x\in \mathbb{R}$
and
$x\in \mathbb{R}$
and
![]() $t\ge 0$
. In this system,
$t\ge 0$
. In this system,
![]() $J*v-v$
models nonlocal dispersal processes of birds;
$J*v-v$
models nonlocal dispersal processes of birds;
![]() $\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\frac{u(t{-}\tau,y)}{u(t{-}\tau,y)+\omega }v(t{-}\tau, y)dy$
is mature mistletoes recruitment, where the integral with a kernel function
$\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\frac{u(t{-}\tau,y)}{u(t{-}\tau,y)+\omega }v(t{-}\tau, y)dy$
is mature mistletoes recruitment, where the integral with a kernel function
![]() $k(x-y)$
expresses the spread of mistletoes fruits by birds from location
$k(x-y)$
expresses the spread of mistletoes fruits by birds from location
![]() $y$
to location
$y$
to location
![]() $x$
and at time
$x$
and at time
![]() $t{-}\tau$
, the Holling type II functional response
$t{-}\tau$
, the Holling type II functional response
![]() $\frac{u}{u+\omega }$
is used to model the fruits removal by birds, and
$\frac{u}{u+\omega }$
is used to model the fruits removal by birds, and
![]() $e^{-d_i\tau }$
represents the probability of the mistletoe from immature survival to maturity; the term
$e^{-d_i\tau }$
represents the probability of the mistletoe from immature survival to maturity; the term
![]() $d\int _{\mathbb{R}}k(x-y)\frac{u(t,y)}{u(t,y)+\omega }v(t, y)dy$
represents the growth of birds caused by eating mistletoe fruits; the other terms and parameters have the same meaning as that in (1.1). We should point out that the background and applications of nonlocal dispersal
$d\int _{\mathbb{R}}k(x-y)\frac{u(t,y)}{u(t,y)+\omega }v(t, y)dy$
represents the growth of birds caused by eating mistletoe fruits; the other terms and parameters have the same meaning as that in (1.1). We should point out that the background and applications of nonlocal dispersal
![]() $J*v-v$
are described in Bates et al. [Reference Bates, Fife, Ren and Wang4], Fife [Reference Fife11], Hutson et al. [Reference Hutson, Martinez, Mischaikow and Vickers13], Lee et al. [Reference Lee15], Murray [Reference Murray23] and Medlock and Kot [Reference Medlock and Kot22]. In the past 20 years, nonlocal dispersal equations have been extensively studied. We refer readers to [Reference Bates, Fife, Ren and Wang4, Reference Carr and Chmaj5, Reference Coville and Dupaigne7, Reference Pan, Li and Lin24, Reference Yu and Yuan32, Reference Zhang, Dong and Li34] for travelling wave solutions, [Reference Chasseigne, Chaves and Rossi6, Reference Ignat and Rossi14] for asymptotic behaviours of solutions for initial boundary value problems, [Reference Fang and Zhao8, Reference Hu, Kuang, Li and Liu12, Reference Li, Wang and Zhao18, Reference Zhang and Ma33] for spreading speeds and [Reference Li, Sun and Wang17, Reference Wu and Ruan30] for entire solutions. The following hypotheses are imposed in [Reference Liang, Weng and Tian19]:
$J*v-v$
are described in Bates et al. [Reference Bates, Fife, Ren and Wang4], Fife [Reference Fife11], Hutson et al. [Reference Hutson, Martinez, Mischaikow and Vickers13], Lee et al. [Reference Lee15], Murray [Reference Murray23] and Medlock and Kot [Reference Medlock and Kot22]. In the past 20 years, nonlocal dispersal equations have been extensively studied. We refer readers to [Reference Bates, Fife, Ren and Wang4, Reference Carr and Chmaj5, Reference Coville and Dupaigne7, Reference Pan, Li and Lin24, Reference Yu and Yuan32, Reference Zhang, Dong and Li34] for travelling wave solutions, [Reference Chasseigne, Chaves and Rossi6, Reference Ignat and Rossi14] for asymptotic behaviours of solutions for initial boundary value problems, [Reference Fang and Zhao8, Reference Hu, Kuang, Li and Liu12, Reference Li, Wang and Zhao18, Reference Zhang and Ma33] for spreading speeds and [Reference Li, Sun and Wang17, Reference Wu and Ruan30] for entire solutions. The following hypotheses are imposed in [Reference Liang, Weng and Tian19]:
-
(H1) Both kernels
 $J(x)$
and
$J(x)$
and
 $k(x)$
are non-negative, symmetric and normalised, i.e.and satisfy
$k(x)$
are non-negative, symmetric and normalised, i.e.and satisfy \begin{gather*} \displaystyle J(x)\ge 0, \quad J(x)=J({-}x)\ge 0, \quad \int _{\mathbb{R}}J(x)dx=1,\\[6pt] \displaystyle k(x)\ge 0, \quad k(x)=k({-}x)\ge 0, \quad \int _{\mathbb{R}}k(x)dx=1, \end{gather*}
\begin{gather*} \displaystyle J(x)\ge 0, \quad J(x)=J({-}x)\ge 0, \quad \int _{\mathbb{R}}J(x)dx=1,\\[6pt] \displaystyle k(x)\ge 0, \quad k(x)=k({-}x)\ge 0, \quad \int _{\mathbb{R}}k(x)dx=1, \end{gather*}
 \begin{gather*} \int _{\mathbb{R}}J(x)e^{-\nu |x|}dx\lt {+}\infty \, \mbox{and}\, \int _{\mathbb{R}}k(x)e^{-\nu |x|}dx\lt {+}\infty \, \mbox{for every}\, \nu \gt 0; \end{gather*}
\begin{gather*} \int _{\mathbb{R}}J(x)e^{-\nu |x|}dx\lt {+}\infty \, \mbox{and}\, \int _{\mathbb{R}}k(x)e^{-\nu |x|}dx\lt {+}\infty \, \mbox{for every}\, \nu \gt 0; \end{gather*}
-
(H2)
 $d_m\lt \tilde d_m\,:\!=\frac{\alpha e^{-d_i\tau }}{\omega }$
.
$d_m\lt \tilde d_m\,:\!=\frac{\alpha e^{-d_i\tau }}{\omega }$
.
It is easy to see that system (1.2) always has a trivial equilibrium
![]() $E_0=(0,0)$
and a boundary equilibrium
$E_0=(0,0)$
and a boundary equilibrium
![]() $E_1=(0,1)$
. If (H2) holds, then there exists a unique positive equilibrium
$E_1=(0,1)$
. If (H2) holds, then there exists a unique positive equilibrium
![]() $E_+\,:\!=(u_+,v_+)$
with
$E_+\,:\!=(u_+,v_+)$
with
 \begin{align*} \begin{cases}\displaystyle u_+\,:\!=\frac{1+d+\sqrt{(1+d)^2-4d\omega \sigma }}{2\sigma }-\omega \gt 0,\\[6pt] \displaystyle v_+\,:\!=1+\frac{du_+}{u_++\omega }\in (1,1+d), \end{cases} \end{align*}
\begin{align*} \begin{cases}\displaystyle u_+\,:\!=\frac{1+d+\sqrt{(1+d)^2-4d\omega \sigma }}{2\sigma }-\omega \gt 0,\\[6pt] \displaystyle v_+\,:\!=1+\frac{du_+}{u_++\omega }\in (1,1+d), \end{cases} \end{align*}
where
![]() $\sigma =\displaystyle\frac{d_m}{\alpha e^{-d_i\tau }}$
. It was proved in [Reference Liang, Weng and Tian19] that
$\sigma =\displaystyle\frac{d_m}{\alpha e^{-d_i\tau }}$
. It was proved in [Reference Liang, Weng and Tian19] that
![]() $E_0$
and
$E_0$
and
![]() $E_1$
are linearly unstable with respect to the corresponding kinetic system, while
$E_1$
are linearly unstable with respect to the corresponding kinetic system, while
![]() $E_+$
is locally asymptotically stable.
$E_+$
is locally asymptotically stable.
It is well known that without birds, the adult mistletoes can only spread in a small area. However, with the nonlocal movements of birds, the mistletoes can invade into new large territories. As such, it is a very interesting problem to model the spatial invasion process of the mistletoes. One way to mathematically characterise this dynamics of the process is travelling wave solution. Travelling wave solutions (in short, travelling waves) of (1.1) are bounded functions with the special form
![]() $(u(t,x),v(t,x))=(\phi (\xi ), \psi (\xi ))$
,
$(u(t,x),v(t,x))=(\phi (\xi ), \psi (\xi ))$
,
![]() $\xi = x+ct$
, which connect two equilibria
$\xi = x+ct$
, which connect two equilibria
![]() $E_1$
and
$E_1$
and
![]() $E_+$
, where
$E_+$
, where
![]() $c\gt 0$
is the wave speed. Clearly, each wave profile
$c\gt 0$
is the wave speed. Clearly, each wave profile
![]() $(\phi,\psi )$
to (1.2) satisfies
$(\phi,\psi )$
to (1.2) satisfies
 \begin{align} \begin{cases} \displaystyle c \phi '(\xi )=\displaystyle -d_m\phi +\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\phi (\xi -y-c\tau )}{\phi (\xi -y-c\tau )+\omega }\psi (\xi -y-c\tau )dy, \\[6pt] \displaystyle c \psi '(\xi )=D(J*\psi -\psi )+\psi (1-\psi )+d\int _{\mathbb{R}}k(y)\frac{\phi (\xi -y)}{\phi (\xi -y)+\omega }\psi (\xi -y)dy,\\[6pt] \displaystyle (\phi,\psi )({-}\infty )=E_1,\quad (\phi,\psi )({+}\infty )=E_+, \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle c \phi '(\xi )=\displaystyle -d_m\phi +\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\phi (\xi -y-c\tau )}{\phi (\xi -y-c\tau )+\omega }\psi (\xi -y-c\tau )dy, \\[6pt] \displaystyle c \psi '(\xi )=D(J*\psi -\psi )+\psi (1-\psi )+d\int _{\mathbb{R}}k(y)\frac{\phi (\xi -y)}{\phi (\xi -y)+\omega }\psi (\xi -y)dy,\\[6pt] \displaystyle (\phi,\psi )({-}\infty )=E_1,\quad (\phi,\psi )({+}\infty )=E_+, \end{cases} \end{align}
where
![]() $(\phi,\psi )({\pm}\infty )=\lim _{\xi \rightarrow {\pm}\infty }(\phi,\psi )(\xi )$
. In [Reference Liang, Weng and Tian19], Liang, Weng and Tian have proved the existence of travelling wave solutions by Schauder’s fixed point theorem and upper-lower solutions technique, i.e. there exists
$(\phi,\psi )({\pm}\infty )=\lim _{\xi \rightarrow {\pm}\infty }(\phi,\psi )(\xi )$
. In [Reference Liang, Weng and Tian19], Liang, Weng and Tian have proved the existence of travelling wave solutions by Schauder’s fixed point theorem and upper-lower solutions technique, i.e. there exists
![]() $c^*$
such that for every
$c^*$
such that for every
![]() $c\ge c^*$
, (1.2) admits a travelling wavefront connecting
$c\ge c^*$
, (1.2) admits a travelling wavefront connecting
![]() $E_1$
and
$E_1$
and
![]() $E_+$
. We should remark that the nonexistence of travelling wavefronts
$E_+$
. We should remark that the nonexistence of travelling wavefronts
![]() $c\lt c^*$
is not addressed in [Reference Liang, Weng and Tian19].
$c\lt c^*$
is not addressed in [Reference Liang, Weng and Tian19].
Another way to characterise the spatial invasion process of the mistletoes into new territories is the spatial invasion speeds (or called asymptotic speeds of spread). The asymptotic speed of spread (in short, spreading speed) was first introduced by Aronson and Weinberger [Reference Aronson, Weinberger and Goldstein1] for reaction-diffusion equations and has been an important ecological metric in a wide range of ecological applications, see e.g. [Reference Aronson and Weinberger2, Reference Liang and Zhao20, Reference Liang and Zhao21] and references therein. Since then, there have been extensive investigations on the spreading speed for various evolution systems, see e.g. [Reference Aronson and Weinberger2, Reference Fang, Wei and Zhao9, Reference Fang, Lan, Seo and Wu10, Reference Li, Weinberger and Lewis16, Reference Liang and Zhao20, Reference Liang and Zhao21, Reference Weinberger, Lewis and Li28, Reference Wu, Weng and Ruan31] and references therein. In this paper, we are devoted to investigating the spreading speeds and travelling wavefronts of (1.2). Since system (1.2) is cooperative and its solution maps are monotone, we shall use the theory in [Reference Liang and Zhao20] to study the existence of spreading speeds for (1.2). Note that the theory of spreading speeds was developed in [Reference Liang and Zhao20] for monotonic systems under a very general setting. The verification of some abstract assumptions in [Reference Liang and Zhao20] is highly nontrivial for the solution maps of (1.2) due to the emergence of nonlocal dispersal and time delay along with nonlocal interaction. In addition, we provide the upper and lower bounds of the established spreading speed.
Finally, we investigate the travelling wavefronts of (1.2). With the help of the spreading features, we derive the nonexistence of travelling wavefronts with speed
![]() $c\in (0, c^*)$
. As mentioned earlier, the existence of travelling wavefronts of (1.2) with speed
$c\in (0, c^*)$
. As mentioned earlier, the existence of travelling wavefronts of (1.2) with speed
![]() $c\ge c^*$
has been obtained by Liang, Weng and Tian [Reference Liang, Weng and Tian19] by using Schauder’s fixed point theorem together with the upper-lower solutions. However, in order to construct a pair of upper-lower solutions successfully, they needed an additional condition (A) and
$c\ge c^*$
has been obtained by Liang, Weng and Tian [Reference Liang, Weng and Tian19] by using Schauder’s fixed point theorem together with the upper-lower solutions. However, in order to construct a pair of upper-lower solutions successfully, they needed an additional condition (A) and
![]() $\omega \ge 1$
. In this paper, we shall remove these assumptions and prove the existence of travelling wavefronts of (1.2) with speed
$\omega \ge 1$
. In this paper, we shall remove these assumptions and prove the existence of travelling wavefronts of (1.2) with speed
![]() $c\ge c^*$
. We appeal to the monotone semiflow method which is different from that in [Reference Liang, Weng and Tian19]. Note that the first equation of system (1.2) has no diffusion term and the diffusion term in the second equation is nonlocal dispersal
$c\ge c^*$
. We appeal to the monotone semiflow method which is different from that in [Reference Liang, Weng and Tian19]. Note that the first equation of system (1.2) has no diffusion term and the diffusion term in the second equation is nonlocal dispersal
![]() $J*v-v$
. Thus, the solution maps associated with (1.2) are not compact with respect to the compact open topology. Therefore, the theory in [Reference Liang and Zhao20] is no longer applicable to prove the existence of travelling wavefronts. Fortunately, the monotone semiflow generated by (1.2) has some weak compactness, and hence, we can use the abstract results in [Reference Fang and Zhao8] to obtain the existence of travelling wavefronts with speed
$J*v-v$
. Thus, the solution maps associated with (1.2) are not compact with respect to the compact open topology. Therefore, the theory in [Reference Liang and Zhao20] is no longer applicable to prove the existence of travelling wavefronts. Fortunately, the monotone semiflow generated by (1.2) has some weak compactness, and hence, we can use the abstract results in [Reference Fang and Zhao8] to obtain the existence of travelling wavefronts with speed
![]() $c\ge c^*$
. Our result shows that the asymptotic speed of spread coincides with the minimal wave speed
$c\ge c^*$
. Our result shows that the asymptotic speed of spread coincides with the minimal wave speed
![]() $c^*$
.
$c^*$
.
This paper is organised as follows. In Section 2, we establish the well-posedness and the comparison principle for the initial value problem. In Section 3, we show the existence of the spreading speed of (1.2) and provide some lower and upper bound estimates of the spreading speed. In Section 4, the existence and nonexistence of travelling wavefronts are investigated.
2. Initial value problem
In this section, we shall investigate the existence and uniqueness theorem of solution to the initial value problem and the comparison theorem. By a change of variables
![]() $U=u$
and
$U=u$
and
![]() $V=v-1$
in (1.2), we obtain
$V=v-1$
in (1.2), we obtain
 \begin{align} \begin{cases} \displaystyle U_t(t,x)=-d_mU+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\frac{U(t{-}\tau,y)}{U(t{-}\tau,y)+\omega }(V(t{-}\tau, y)+1)dy, \\[6pt] \displaystyle V_t(t,x)=D(J*V-V)-V(V+1)+d\int _{\mathbb{R}}k(x-y)\frac{U(t,y)}{U(t,y)+\omega }(V(t, y)+1)dy. \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle U_t(t,x)=-d_mU+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\frac{U(t{-}\tau,y)}{U(t{-}\tau,y)+\omega }(V(t{-}\tau, y)+1)dy, \\[6pt] \displaystyle V_t(t,x)=D(J*V-V)-V(V+1)+d\int _{\mathbb{R}}k(x-y)\frac{U(t,y)}{U(t,y)+\omega }(V(t, y)+1)dy. \end{cases} \end{align}
The spatially homogeneous system associated with (2.1) is
 \begin{align} \begin{cases} \displaystyle U'=\frac{\alpha e^{-d_{i}\tau }U(t{-}\tau )(V(t{-}\tau )+1)}{U(t{-}\tau )+\omega }-d_mU, \\[6pt] \displaystyle V'=-V(1+V)+\frac{dU(V+1)}{U+\omega }. \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle U'=\frac{\alpha e^{-d_{i}\tau }U(t{-}\tau )(V(t{-}\tau )+1)}{U(t{-}\tau )+\omega }-d_mU, \\[6pt] \displaystyle V'=-V(1+V)+\frac{dU(V+1)}{U+\omega }. \end{cases} \end{align}
It is easy to see that the equilibria of (1.2), respectively, become
For the convenience, in what follows, we let
![]() $\tilde u_+=u_+$
and
$\tilde u_+=u_+$
and
![]() $\tilde v_+=v_+-1$
. Now we consider the corresponding initial value problem of (2.1):
$\tilde v_+=v_+-1$
. Now we consider the corresponding initial value problem of (2.1):
 \begin{align} \begin{cases} \displaystyle U_t(t,x)=-d_mU+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\frac{U(t{-}\tau,y)}{U(t{-}\tau,y)+\omega }(V(t{-}\tau, y)+1)dy, \\[6pt] \displaystyle V_t(t,x)=D(J*V-V)-V(V+1)+d\int _{\mathbb{R}}k(x-y)\frac{U(t,y)}{U(t,y)+\omega }(V(t, y)+1)dy,\\[6pt] \displaystyle U(s,x)=\phi _1(s,x),\quad V(s,x)=\phi _2(s,x),\quad (s,x)\in [{-}\tau,0]\times \mathbb{R}. \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle U_t(t,x)=-d_mU+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\frac{U(t{-}\tau,y)}{U(t{-}\tau,y)+\omega }(V(t{-}\tau, y)+1)dy, \\[6pt] \displaystyle V_t(t,x)=D(J*V-V)-V(V+1)+d\int _{\mathbb{R}}k(x-y)\frac{U(t,y)}{U(t,y)+\omega }(V(t, y)+1)dy,\\[6pt] \displaystyle U(s,x)=\phi _1(s,x),\quad V(s,x)=\phi _2(s,x),\quad (s,x)\in [{-}\tau,0]\times \mathbb{R}. \end{cases} \end{align}
We begin with some notation. The proper phase space for (2.3) can be chosen as
![]() $\mathcal{C}\,:\!=C ([{-}\tau,0]\times \mathbb{R},\mathbb{R}^2)$
. Clearly, any vector in
$\mathcal{C}\,:\!=C ([{-}\tau,0]\times \mathbb{R},\mathbb{R}^2)$
. Clearly, any vector in
![]() $\mathbb{R}^2$
(which is constant in
$\mathbb{R}^2$
(which is constant in
![]() $(t,x)$
), or any element in
$(t,x)$
), or any element in
![]() $\bar{\mathcal{C}}\,:\!=C ([{-}\tau,0],\mathbb{R}^2)$
(which is constant in
$\bar{\mathcal{C}}\,:\!=C ([{-}\tau,0],\mathbb{R}^2)$
(which is constant in
![]() $x$
), can be regarded as an element in
$x$
), can be regarded as an element in
![]() $\mathcal{C}$
. A natural order “
$\mathcal{C}$
. A natural order “
![]() $\geq$
” in
$\geq$
” in
![]() $\mathcal{C}$
is defined by
$\mathcal{C}$
is defined by
![]() $u\geq v$
for
$u\geq v$
for
![]() $u=(u_1,u_2)$
and
$u=(u_1,u_2)$
and
![]() $v=(v_1,v_2)\in \mathcal{C}$
, if
$v=(v_1,v_2)\in \mathcal{C}$
, if
![]() $u_i(s,x)\geq v_i(s, x)$
for
$u_i(s,x)\geq v_i(s, x)$
for
![]() $i=1, 2$
,
$i=1, 2$
,
![]() $s\in [{-}\tau,0]$
and
$s\in [{-}\tau,0]$
and
![]() $x\in \mathbb{R}$
;
$x\in \mathbb{R}$
;
![]() $u\gt v$
if
$u\gt v$
if
![]() $u\geq v$
and
$u\geq v$
and
![]() $u\neq v$
; and
$u\neq v$
; and
![]() $u\gg v$
if
$u\gg v$
if
![]() $u_i(s,x)\gt v_i(s, x)$
. For any
$u_i(s,x)\gt v_i(s, x)$
. For any
![]() $\mathbf{r}\in \mathbb{R}^2$
and
$\mathbf{r}\in \mathbb{R}^2$
and
![]() $\mathbf{r}\geq 0$
, defined
$\mathbf{r}\geq 0$
, defined
![]() $\mathcal{C}_{\mathbf{r}}\,:\!=\{\phi \in \mathcal{C}\,{:}\,\mathbf{0}\leq \phi \leq \mathbf{r}\}$
and
$\mathcal{C}_{\mathbf{r}}\,:\!=\{\phi \in \mathcal{C}\,{:}\,\mathbf{0}\leq \phi \leq \mathbf{r}\}$
and
![]() $\bar{\mathcal{C}_{\mathbf{r}}}\,:\!=\{\phi \in \bar{\mathcal{C}}\,{:}\,\mathbf{0}\leq \phi \leq \mathbf{r}\}$
. Moreover, let
$\bar{\mathcal{C}_{\mathbf{r}}}\,:\!=\{\phi \in \bar{\mathcal{C}}\,{:}\,\mathbf{0}\leq \phi \leq \mathbf{r}\}$
. Moreover, let
![]() $X\,:\!=BC(\mathbb{R},\mathbb{R}^2)$
be the set of all bounded continuous functions from
$X\,:\!=BC(\mathbb{R},\mathbb{R}^2)$
be the set of all bounded continuous functions from
![]() $\mathbb{R}$
to
$\mathbb{R}$
to
![]() $\mathbb{R}^2$
, and
$\mathbb{R}^2$
, and
![]() $X_{\mathbf{r}}\,:\!=\{\phi \in X\,{:}\,\mathbf{0}\leq \phi \leq \mathbf{r}\}$
.
$X_{\mathbf{r}}\,:\!=\{\phi \in X\,{:}\,\mathbf{0}\leq \phi \leq \mathbf{r}\}$
.
We first study the existence and uniqueness of solution to the initial value problem (2.3).
Lemma 2.1.
For any initial value
![]() $\phi \,:\!= (\phi _1,\phi _2)\in \mathcal{C}_{\mathbf{K}}$
, (2.3) admits a unique solution
$\phi \,:\!= (\phi _1,\phi _2)\in \mathcal{C}_{\mathbf{K}}$
, (2.3) admits a unique solution
![]() $(U(t,x;\,\phi ), V(t,x;\,\phi ))$
satisfying
$(U(t,x;\,\phi ), V(t,x;\,\phi ))$
satisfying
Proof. Let
![]() $\beta \gt 0$
. Then, system (2.3) can be rewritten as
$\beta \gt 0$
. Then, system (2.3) can be rewritten as
 \begin{align} \begin{cases} \displaystyle U_t= -(\beta +d_m)U + \mathcal{F}_1[U,V](t,x), \, \, t\gt 0, \, x\in \mathbb{R}, \\[6pt] \displaystyle V_t= -(\beta +1)V + \mathcal{F}_2[U,V](t,x), \, \, \, \, t\gt 0, \, x\in \mathbb{R}, \\[6pt] \displaystyle U(s,x)\,:\!=\phi _1(s,x), \, \, \, \, {-}\tau \leq s\leq 0, \, x\in \mathbb{R}, \\[6pt] \displaystyle V(s,x)\,:\!=\phi _2(s,x), \, \, \, \, {-}\tau \leq s\leq 0, \, x\in \mathbb{R}, \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle U_t= -(\beta +d_m)U + \mathcal{F}_1[U,V](t,x), \, \, t\gt 0, \, x\in \mathbb{R}, \\[6pt] \displaystyle V_t= -(\beta +1)V + \mathcal{F}_2[U,V](t,x), \, \, \, \, t\gt 0, \, x\in \mathbb{R}, \\[6pt] \displaystyle U(s,x)\,:\!=\phi _1(s,x), \, \, \, \, {-}\tau \leq s\leq 0, \, x\in \mathbb{R}, \\[6pt] \displaystyle V(s,x)\,:\!=\phi _2(s,x), \, \, \, \, {-}\tau \leq s\leq 0, \, x\in \mathbb{R}, \end{cases} \end{align}
where
![]() $(\mathcal{F}_1,\mathcal{F}_2)$
is defined on
$(\mathcal{F}_1,\mathcal{F}_2)$
is defined on
![]() $C([{-}\tau,\infty ]\times \mathbb{R}, I)$
, with
$C([{-}\tau,\infty ]\times \mathbb{R}, I)$
, with
![]() $I=[0,\tilde{u}_+]\times [0,\tilde{v}_+]$
, by
$I=[0,\tilde{u}_+]\times [0,\tilde{v}_+]$
, by
 \begin{align*} \begin{cases} \displaystyle \mathcal{F}_1[U,V](t,x)\,:\!=\beta U+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{U(t{-}\tau,x-y)}{U(t{-}\tau,x-y)+\omega }(V(t{-}\tau,x-y)+1)dy,\\[6pt] \displaystyle \mathcal{F}_2[U,V](t,x)\,:\!=\beta V-V^2+d\int _{\mathbb{R}}k(y)\frac{U(t,x-y)}{U(t,x-y)+\omega }(V(t,x-y)+1)dy \\[6pt] \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,\displaystyle +D\int _{\mathbb{R}}J(y)[V(t,x-y)-V(t,x)]dy \end{cases} \end{align*}
\begin{align*} \begin{cases} \displaystyle \mathcal{F}_1[U,V](t,x)\,:\!=\beta U+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{U(t{-}\tau,x-y)}{U(t{-}\tau,x-y)+\omega }(V(t{-}\tau,x-y)+1)dy,\\[6pt] \displaystyle \mathcal{F}_2[U,V](t,x)\,:\!=\beta V-V^2+d\int _{\mathbb{R}}k(y)\frac{U(t,x-y)}{U(t,x-y)+\omega }(V(t,x-y)+1)dy \\[6pt] \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,\displaystyle +D\int _{\mathbb{R}}J(y)[V(t,x-y)-V(t,x)]dy \end{cases} \end{align*}
for
![]() $t\in (0,\infty )$
. It is easy to verify that if we choose
$t\in (0,\infty )$
. It is easy to verify that if we choose
![]() $\beta$
large enough, then
$\beta$
large enough, then
![]() $\mathcal{F}_i$
is nondecreasing in
$\mathcal{F}_i$
is nondecreasing in
![]() $U$
and
$U$
and
![]() $V$
,
$V$
,
![]() $i=1,2$
. Obviously, system (2.4) is equivalent to the following integral system
$i=1,2$
. Obviously, system (2.4) is equivalent to the following integral system
 \begin{align} \begin{cases} \displaystyle U(t,x)= e^{-(\beta +d_m)t}\phi _1(0,x) +\int _0^te^{-(\beta +d_m)(t-r)}\mathcal{F}_1[U,V](r,x)dr, \\[6pt] \displaystyle V(t,x)= e^{-(\beta +1)t}\phi _2(0,x) +\int _0^te^{-(\beta +1)(t-r)}\mathcal{F}_2[U,V](r,x)dr, \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle U(t,x)= e^{-(\beta +d_m)t}\phi _1(0,x) +\int _0^te^{-(\beta +d_m)(t-r)}\mathcal{F}_1[U,V](r,x)dr, \\[6pt] \displaystyle V(t,x)= e^{-(\beta +1)t}\phi _2(0,x) +\int _0^te^{-(\beta +1)(t-r)}\mathcal{F}_2[U,V](r,x)dr, \end{cases} \end{align}
for
![]() $t\gt 0$
and
$t\gt 0$
and
![]() $x\in \mathbb{R}$
.
$x\in \mathbb{R}$
.
Define the set
and an operator
![]() $\mathcal{G}=(\mathcal{G}_1, \mathcal{G}_2)\,{:}\,\Gamma \rightarrow \Gamma$
by
$\mathcal{G}=(\mathcal{G}_1, \mathcal{G}_2)\,{:}\,\Gamma \rightarrow \Gamma$
by
 \begin{align*} \begin{cases} \displaystyle \mathcal{G}_1[U,V](t,x)\,:\!= e^{-(\beta +d_m)t}\phi _1(0,x) +\int _0^te^{-(\beta +d_m)(t-r)}\mathcal{F}_1[U,V](r,x)dr, \\[6pt] \displaystyle \mathcal{G}_2[U,V](t,x)\,:\!= e^{-(\beta +1)t}\phi _2(0,x) +\int _0^te^{-(\beta +1)(t-r)}\mathcal{F}_2[U,V](r,x)dr, \end{cases} \end{align*}
\begin{align*} \begin{cases} \displaystyle \mathcal{G}_1[U,V](t,x)\,:\!= e^{-(\beta +d_m)t}\phi _1(0,x) +\int _0^te^{-(\beta +d_m)(t-r)}\mathcal{F}_1[U,V](r,x)dr, \\[6pt] \displaystyle \mathcal{G}_2[U,V](t,x)\,:\!= e^{-(\beta +1)t}\phi _2(0,x) +\int _0^te^{-(\beta +1)(t-r)}\mathcal{F}_2[U,V](r,x)dr, \end{cases} \end{align*}
where
![]() $(t,x)\in \mathbb{R}_+\times \mathbb{R}$
. For any
$(t,x)\in \mathbb{R}_+\times \mathbb{R}$
. For any
![]() $(U,V)\in \Gamma$
, by the monotonicity of
$(U,V)\in \Gamma$
, by the monotonicity of
![]() $\mathcal{F}_i$
, we have
$\mathcal{F}_i$
, we have
 \begin{align*} 0\leq \mathcal{G}_1[U,V](t,x)&\leq e^{-(\beta +d_m)t}\tilde{u}_+ + \mathcal{F}_1[\tilde{u}_+,\tilde{v}_+]\int _0^te^{-(\beta +d_m)(t-r)}dr \\ &\leq e^{-(\beta +d_m)t}\tilde{u}_+ + \tilde{u}_+(1-e^{-(\beta +d_m)t})=\tilde{u}_+ \end{align*}
\begin{align*} 0\leq \mathcal{G}_1[U,V](t,x)&\leq e^{-(\beta +d_m)t}\tilde{u}_+ + \mathcal{F}_1[\tilde{u}_+,\tilde{v}_+]\int _0^te^{-(\beta +d_m)(t-r)}dr \\ &\leq e^{-(\beta +d_m)t}\tilde{u}_+ + \tilde{u}_+(1-e^{-(\beta +d_m)t})=\tilde{u}_+ \end{align*}
and
 \begin{align*} 0\leq \mathcal{G}_2[U,V](t,x)&\leq e^{-(\beta +1)t}\tilde{v}_+ + \mathcal{F}_2[\tilde{u}_+,\tilde{v}_+]\int _0^te^{-(\beta +1)(t-r)}dr \\ &\leq e^{-(\beta +1)t}\tilde{v}_+ + \tilde{v}_+(1-e^{-(\beta +1)t})=\tilde{v}_+, \end{align*}
\begin{align*} 0\leq \mathcal{G}_2[U,V](t,x)&\leq e^{-(\beta +1)t}\tilde{v}_+ + \mathcal{F}_2[\tilde{u}_+,\tilde{v}_+]\int _0^te^{-(\beta +1)(t-r)}dr \\ &\leq e^{-(\beta +1)t}\tilde{v}_+ + \tilde{v}_+(1-e^{-(\beta +1)t})=\tilde{v}_+, \end{align*}
and hence,
![]() $\mathcal{G}(\Gamma )\subseteq \Gamma$
.
$\mathcal{G}(\Gamma )\subseteq \Gamma$
.
For
![]() $\mu \gt 0$
and
$\mu \gt 0$
and
![]() $(U,V)\in \Gamma$
, we define
$(U,V)\in \Gamma$
, we define
 \begin{align*} \|(U,V)\|_\mu &=\sup _{t\in [{-}\tau,0],x\in \mathbb{R}}(|U(t,x)|+|V(t,x)|) \\ &\quad + \sup _{t\in [0,{+}\infty ),x\in \mathbb{R}}(|U(t,x)|+|V(t,x)|)e^{-\mu t},\\ d_\mu (w_1,w_2)&\,:\!=\|w_1-w_2\|_\mu, \end{align*}
\begin{align*} \|(U,V)\|_\mu &=\sup _{t\in [{-}\tau,0],x\in \mathbb{R}}(|U(t,x)|+|V(t,x)|) \\ &\quad + \sup _{t\in [0,{+}\infty ),x\in \mathbb{R}}(|U(t,x)|+|V(t,x)|)e^{-\mu t},\\ d_\mu (w_1,w_2)&\,:\!=\|w_1-w_2\|_\mu, \end{align*}
where
![]() $w_1=(U_1,V_1)$
and
$w_1=(U_1,V_1)$
and
![]() $w_2=(U_2, V_2)$
. Then,
$w_2=(U_2, V_2)$
. Then,
![]() $(\Gamma, d_\mu )$
is a complete metric space. For any
$(\Gamma, d_\mu )$
is a complete metric space. For any
![]() $(U,V), (\overline{U},\overline{V})\in \Gamma$
, we obtain
$(U,V), (\overline{U},\overline{V})\in \Gamma$
, we obtain
 \begin{align*} &|\mathcal{G}_1[U,V]-\mathcal{G}_1[\overline{U},\overline{V}]| \\[4pt] &\quad\leq \int _0^t\beta e^{-(\beta +d_m)(t-r)}|U-\overline{U}|(r,x)dr \\[4pt] &\qquad + \int _0^te^{-(\beta +d_m)(t-r)}\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\Bigl |\frac{U(r{-}\tau,x-y)}{U(r{-}\tau,x-y)+\omega }(V(r{-}\tau,x-y)+1) \\[4pt] &\qquad - \frac{\overline{U}(r{-}\tau,x-y)}{\overline{U}(r{-}\tau,x-y)+\omega }(\overline{V}(r{-}\tau,x-y)+1)\Bigr |dydr \\[4pt] &\quad\leq \int _0^t\beta e^{-(\beta +d_m)(t-r)}|U-\overline{U}|(r,x)dr +\alpha e^{-d_i\tau }\int _0^t\int _{\mathbb{R}}e^{-(\beta +d_m)(t-r)}k(y) \\[4pt] &\qquad \times \left [\frac{\tilde{v}_+}{\omega }|U-\overline{U}|(r{-}\tau,x-y)+|V-\overline{V}|(r{-}\tau,x-y)\right ] dydr, \end{align*}
\begin{align*} &|\mathcal{G}_1[U,V]-\mathcal{G}_1[\overline{U},\overline{V}]| \\[4pt] &\quad\leq \int _0^t\beta e^{-(\beta +d_m)(t-r)}|U-\overline{U}|(r,x)dr \\[4pt] &\qquad + \int _0^te^{-(\beta +d_m)(t-r)}\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\Bigl |\frac{U(r{-}\tau,x-y)}{U(r{-}\tau,x-y)+\omega }(V(r{-}\tau,x-y)+1) \\[4pt] &\qquad - \frac{\overline{U}(r{-}\tau,x-y)}{\overline{U}(r{-}\tau,x-y)+\omega }(\overline{V}(r{-}\tau,x-y)+1)\Bigr |dydr \\[4pt] &\quad\leq \int _0^t\beta e^{-(\beta +d_m)(t-r)}|U-\overline{U}|(r,x)dr +\alpha e^{-d_i\tau }\int _0^t\int _{\mathbb{R}}e^{-(\beta +d_m)(t-r)}k(y) \\[4pt] &\qquad \times \left [\frac{\tilde{v}_+}{\omega }|U-\overline{U}|(r{-}\tau,x-y)+|V-\overline{V}|(r{-}\tau,x-y)\right ] dydr, \end{align*}
and hence,
 \begin{align*} &|\mathcal{G}_1[U,V]-\mathcal{G}_1[\overline{U},\overline{V}]|e^{-\mu t} \\[4pt] &\quad\leq \int _0^t\beta e^{-(\beta +d_m+\mu )(t-r)}e^{-\mu r}|U-\overline{U}|(r,x)dr +\alpha e^{-d_i\tau }\int _0^t\int _{\mathbb{R}}e^{-(\beta +d_m+\mu )(t-r)}k(y) \\[4pt] &\qquad \times \left [\frac{\tilde{v}_+}{\omega }e^{-\mu r}|U-\overline{U}|(r{-}\tau,x-y)+e^{-\mu r}|V-\overline{V}|(r{-}\tau,x-y)\right ] dydr. \end{align*}
\begin{align*} &|\mathcal{G}_1[U,V]-\mathcal{G}_1[\overline{U},\overline{V}]|e^{-\mu t} \\[4pt] &\quad\leq \int _0^t\beta e^{-(\beta +d_m+\mu )(t-r)}e^{-\mu r}|U-\overline{U}|(r,x)dr +\alpha e^{-d_i\tau }\int _0^t\int _{\mathbb{R}}e^{-(\beta +d_m+\mu )(t-r)}k(y) \\[4pt] &\qquad \times \left [\frac{\tilde{v}_+}{\omega }e^{-\mu r}|U-\overline{U}|(r{-}\tau,x-y)+e^{-\mu r}|V-\overline{V}|(r{-}\tau,x-y)\right ] dydr. \end{align*}
Similarly, one has
 \begin{align*} &|\mathcal{G}_2[U,V]-\mathcal{G}_2[\overline{U},\overline{V}]| \\[4pt] &\quad\leq \int _0^t e^{-(\beta +1)(t-r)}\left [\beta |V-\overline{V}|+|V^2-\overline{V}^2|\right ]dr \\[4pt] &\qquad + \int _0^te^{-(\beta +1)(t-r)}d\int _{\mathbb{R}}k(y)\Bigl |\frac{U(r,x-y)}{U(r,x-y)+\omega }(V(r,x-y)+1) \\[4pt] &\qquad - \frac{\overline{U}(r,x-y)}{\overline{U}(r,x-y)+\omega }(\overline{V}(r,x-y)+1)\Bigr |dydr \\[4pt] &\qquad + \int _0^te^{-(\beta +1)(t-r)}D\int _{\mathbb{R}}J(y)\left [|V-\overline{V}|(r,x-y)+|V-\overline{V}|(r,x)\right ]dydr \\[4pt] &\quad\leq \int _0^t(\beta +D+2(\tilde{v}_+-1)) e^{-(\beta +1)(t-r)}|V-\overline{V}|(r,x)dr \\[4pt] &\qquad + d\int _0^t\int _{\mathbb{R}}e^{-(\beta +1)(t-r)}k(y)\left [\frac{\tilde{v}_+}{\omega }|U-\overline{U}|(r,x-y)+|V-\overline{V}|(r,x-y)\right ] dydr \\[4pt] &\qquad + D\int _0^t\int _{\mathbb{R}}e^{-(\beta +1)(t-r)}J(y)|V-\overline{V}|(r,x-y)dydr, \end{align*}
\begin{align*} &|\mathcal{G}_2[U,V]-\mathcal{G}_2[\overline{U},\overline{V}]| \\[4pt] &\quad\leq \int _0^t e^{-(\beta +1)(t-r)}\left [\beta |V-\overline{V}|+|V^2-\overline{V}^2|\right ]dr \\[4pt] &\qquad + \int _0^te^{-(\beta +1)(t-r)}d\int _{\mathbb{R}}k(y)\Bigl |\frac{U(r,x-y)}{U(r,x-y)+\omega }(V(r,x-y)+1) \\[4pt] &\qquad - \frac{\overline{U}(r,x-y)}{\overline{U}(r,x-y)+\omega }(\overline{V}(r,x-y)+1)\Bigr |dydr \\[4pt] &\qquad + \int _0^te^{-(\beta +1)(t-r)}D\int _{\mathbb{R}}J(y)\left [|V-\overline{V}|(r,x-y)+|V-\overline{V}|(r,x)\right ]dydr \\[4pt] &\quad\leq \int _0^t(\beta +D+2(\tilde{v}_+-1)) e^{-(\beta +1)(t-r)}|V-\overline{V}|(r,x)dr \\[4pt] &\qquad + d\int _0^t\int _{\mathbb{R}}e^{-(\beta +1)(t-r)}k(y)\left [\frac{\tilde{v}_+}{\omega }|U-\overline{U}|(r,x-y)+|V-\overline{V}|(r,x-y)\right ] dydr \\[4pt] &\qquad + D\int _0^t\int _{\mathbb{R}}e^{-(\beta +1)(t-r)}J(y)|V-\overline{V}|(r,x-y)dydr, \end{align*}
and hence,
 \begin{align*} &|\mathcal{G}_2[U,V]-\mathcal{G}_2[\overline{U},\overline{V}]|e^{-\mu t} \\ &\quad\leq \int _0^t(\beta +D+2(\tilde{v}_+-1)) e^{-(\beta +1+\mu )(t-r)}e^{-\mu r}|V-\overline{V}|(r,x)dr \\ &\qquad + d\int _0^t\int _{\mathbb{R}}e^{-(\beta +1+\mu )(t-r)}k(y) \\ &\qquad \times \left [\frac{\tilde{v}_+}{\omega }e^{-\mu r}|U-\overline{U}|(r,x-y)+e^{-\mu r}|V-\overline{V}|(r,x-y)\right ] dydr \\ &\qquad + D\int _0^t\int _{\mathbb{R}}e^{-(\beta +1+\mu )(t-r)}J(y)e^{-\mu r}|V-\overline{V}|(r,x-y)dydr. \end{align*}
\begin{align*} &|\mathcal{G}_2[U,V]-\mathcal{G}_2[\overline{U},\overline{V}]|e^{-\mu t} \\ &\quad\leq \int _0^t(\beta +D+2(\tilde{v}_+-1)) e^{-(\beta +1+\mu )(t-r)}e^{-\mu r}|V-\overline{V}|(r,x)dr \\ &\qquad + d\int _0^t\int _{\mathbb{R}}e^{-(\beta +1+\mu )(t-r)}k(y) \\ &\qquad \times \left [\frac{\tilde{v}_+}{\omega }e^{-\mu r}|U-\overline{U}|(r,x-y)+e^{-\mu r}|V-\overline{V}|(r,x-y)\right ] dydr \\ &\qquad + D\int _0^t\int _{\mathbb{R}}e^{-(\beta +1+\mu )(t-r)}J(y)e^{-\mu r}|V-\overline{V}|(r,x-y)dydr. \end{align*}
Let
It then follows that
 \begin{align*} \|\mathcal{G}[U,V]-\mathcal{G}[\overline{U},\overline{V}]\|_{\mu } & \leq 2M\int _0^t e^{-(\beta _0+\mu )}(t-r)\|(U,V)-\overline{U},\overline{V}\|_{\mu }dr \\ & \leq \frac{2M}{\beta _0+\mu }\|(U,V)-(\overline{U},\overline{V})\|_{\mu }. \end{align*}
\begin{align*} \|\mathcal{G}[U,V]-\mathcal{G}[\overline{U},\overline{V}]\|_{\mu } & \leq 2M\int _0^t e^{-(\beta _0+\mu )}(t-r)\|(U,V)-\overline{U},\overline{V}\|_{\mu }dr \\ & \leq \frac{2M}{\beta _0+\mu }\|(U,V)-(\overline{U},\overline{V})\|_{\mu }. \end{align*}
Choose
![]() $\mu \gt 0$
large enough such that
$\mu \gt 0$
large enough such that
![]() $\frac{2M}{\beta _0+\mu }\lt 1$
. Then,
$\frac{2M}{\beta _0+\mu }\lt 1$
. Then,
![]() $\mathcal{G}$
is a contracting mapping in
$\mathcal{G}$
is a contracting mapping in
![]() $\Gamma$
. By the contraction mapping theorem, we see that
$\Gamma$
. By the contraction mapping theorem, we see that
![]() $\mathcal{G}$
has a unique fixed point in
$\mathcal{G}$
has a unique fixed point in
![]() $\Gamma$
, which is the solution of (2.3). The proof is complete.
$\Gamma$
, which is the solution of (2.3). The proof is complete.
Next, we establish the comparison principle for upper and lower solutions of (2.3). For this purpose, we introduce the definition of upper and lower solutions.
Definition 2.2.
A function
![]() $(\overline{U},\overline{V})\in C^1([{-}\tau,\infty ), X_{\mathbf{K}})$
is called an upper solution of (2.3) if it satisfies
$(\overline{U},\overline{V})\in C^1([{-}\tau,\infty ), X_{\mathbf{K}})$
is called an upper solution of (2.3) if it satisfies
 \begin{align} \begin{cases} \displaystyle\frac{\partial \overline{U}}{\partial t}\geq -d_{m}\overline{U}(t,x)+\alpha e^{-d_i\tau }\int _{\Omega }k(y)\frac{\overline{U}(t{-}\tau, x-y)}{\overline{U}(t{-}\tau, x-y)+\omega }(\overline{V}(t{-}\tau, x-y)+1)dy, \\[6pt] \displaystyle \frac{\partial \overline{V}}{\partial t}\geq D\int _{\mathbb{R}}J(y)\left [\overline{V}(t, x-y)-\overline{V}(t, x)\right ]dy-\overline{V}(1+\overline{V}) \\[6pt] \, \, \, \, \, \, \, \,\displaystyle +d\int _{\Omega }k(y)\frac{\overline{U}(t, x-y)}{\overline{U}(t, x-y)+\omega }(\overline{V}(t, x-y)+1)dy,\\[6pt] \displaystyle \overline{U}(s,x)\ge \phi _1(s,x),\quad \overline{V}(s,x)\ge \phi _2(s,x),\quad (s,x)\in [{-}\tau,0]\times \mathbb{R}, \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle\frac{\partial \overline{U}}{\partial t}\geq -d_{m}\overline{U}(t,x)+\alpha e^{-d_i\tau }\int _{\Omega }k(y)\frac{\overline{U}(t{-}\tau, x-y)}{\overline{U}(t{-}\tau, x-y)+\omega }(\overline{V}(t{-}\tau, x-y)+1)dy, \\[6pt] \displaystyle \frac{\partial \overline{V}}{\partial t}\geq D\int _{\mathbb{R}}J(y)\left [\overline{V}(t, x-y)-\overline{V}(t, x)\right ]dy-\overline{V}(1+\overline{V}) \\[6pt] \, \, \, \, \, \, \, \,\displaystyle +d\int _{\Omega }k(y)\frac{\overline{U}(t, x-y)}{\overline{U}(t, x-y)+\omega }(\overline{V}(t, x-y)+1)dy,\\[6pt] \displaystyle \overline{U}(s,x)\ge \phi _1(s,x),\quad \overline{V}(s,x)\ge \phi _2(s,x),\quad (s,x)\in [{-}\tau,0]\times \mathbb{R}, \end{cases} \end{align}
for all
![]() $(t,x)\in [0,\infty )\times \mathbb{R}$
. A lower solution of (2.3) is defined in a similar way by reversing the inequalities in (2.6).
$(t,x)\in [0,\infty )\times \mathbb{R}$
. A lower solution of (2.3) is defined in a similar way by reversing the inequalities in (2.6).
Lemma 2.3.
Let
![]() $(\overline{U},\overline{V})$
and
$(\overline{U},\overline{V})$
and
![]() $(\underline{U},\underline{V})$
be a pair of upper and lower solutions of (2.3). Then,
$(\underline{U},\underline{V})$
be a pair of upper and lower solutions of (2.3). Then,
![]() $\overline{U}(t,x)\geq \underline{U}(t,x)$
and
$\overline{U}(t,x)\geq \underline{U}(t,x)$
and
![]() $\overline{V}(t,x)\geq \underline{V}(t,x)$
for all
$\overline{V}(t,x)\geq \underline{V}(t,x)$
for all
![]() $t\geq 0$
and
$t\geq 0$
and
![]() $x\in \mathbb{R}$
.
$x\in \mathbb{R}$
.
Proof. Let
![]() $W_1(t,x)\,:\!=\overline{U}(t,x)-\underline{U}(t,x)$
,
$W_1(t,x)\,:\!=\overline{U}(t,x)-\underline{U}(t,x)$
,
![]() $W_2(t,x)\,:\!=\overline{V}(t,x)-\underline{V}(t,x)$
,
$W_2(t,x)\,:\!=\overline{V}(t,x)-\underline{V}(t,x)$
,
![]() $\forall (t,x)\in \mathbb{R}_+\times \mathbb{R}$
, and
$\forall (t,x)\in \mathbb{R}_+\times \mathbb{R}$
, and
It then follows that
![]() $W(t)$
is a continuous function. We shall prove that
$W(t)$
is a continuous function. We shall prove that
![]() $W(t)\geq 0$
,
$W(t)\geq 0$
,
![]() $\forall t\geq 0$
. Assume, by contradiction, that the assertion is not true. Then, there exists a number
$\forall t\geq 0$
. Assume, by contradiction, that the assertion is not true. Then, there exists a number
![]() $t_0\gt 0$
such that
$t_0\gt 0$
such that
![]() $W(t_0)\lt 0$
. Since
$W(t_0)\lt 0$
. Since
![]() $W(t)e^{-\delta t}$
with
$W(t)e^{-\delta t}$
with
![]() $\delta \gt 0$
is continuous and
$\delta \gt 0$
is continuous and
![]() $W(0)\ge 0$
. By the property of continuous function, without loss of generality, for such
$W(0)\ge 0$
. By the property of continuous function, without loss of generality, for such
![]() $t_0$
, we have
$t_0$
, we have
Thus, there exist an index
![]() $i\in \{1,2\}$
and a sequence of points
$i\in \{1,2\}$
and a sequence of points
![]() $\{x_k\}_{k=1}^\infty$
such that
$\{x_k\}_{k=1}^\infty$
such that
![]() $W_i(t_0,x_k)\lt 0$
,
$W_i(t_0,x_k)\lt 0$
,
![]() $\forall k\ge 1$
and
$\forall k\ge 1$
and
![]() $\lim \limits _{k\rightarrow \infty }W_i(t_0,x_k)=W(t_0)$
. Let
$\lim \limits _{k\rightarrow \infty }W_i(t_0,x_k)=W(t_0)$
. Let
![]() $\{t_k\}_{k=1}^\infty \subset [0,t_0]$
be a sequence such that
$\{t_k\}_{k=1}^\infty \subset [0,t_0]$
be a sequence such that
Moreover,
![]() $\{x_k\}_{k=1}^\infty$
can be chosen properly as local minimisers of
$\{x_k\}_{k=1}^\infty$
can be chosen properly as local minimisers of
![]() $W_i(t_k,x)$
. Then, we obtain that
$W_i(t_k,x)$
. Then, we obtain that
![]() $\int _{\mathbb{R}}J(y)[W_i(t_k,x_k-y)-W_i(t_k,x_k)]dy\geq 0$
. By a similar argument as that in [Reference Weng and Zhao29, Theorem 2.2], we can obtain that
$\int _{\mathbb{R}}J(y)[W_i(t_k,x_k-y)-W_i(t_k,x_k)]dy\geq 0$
. By a similar argument as that in [Reference Weng and Zhao29, Theorem 2.2], we can obtain that
![]() $\displaystyle\frac{\partial W_i(t_k,x_k)}{\partial t}\leq \delta W_i(t_k,x_k)$
. Hence, we further have
$\displaystyle\frac{\partial W_i(t_k,x_k)}{\partial t}\leq \delta W_i(t_k,x_k)$
. Hence, we further have
 \begin{align*} 0\leq & \frac{\partial W_1(t_k,x_k)}{\partial t}+d_m W_1(t_k,x_k) \\[4pt] & -\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\overline{U}(t_k{-}\tau, x_k-y)}{\overline{U}(t_k{-}\tau, x_k-y)+\omega }(\overline{V}(t_k{-}\tau, x_k-y)+1)dy \\[4pt] & +\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\underline{U}(t_k{-}\tau, x_k-y)}{\underline{U}(t_k{-}\tau, x_k-y)+\omega }(\underline{V}(t_k{-}\tau, x_k-y)+1)dy \\[4pt] \leq & (\delta +d_m)W_1(t_k,x_k)-\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\overline{U}}{\overline{U}+\omega }W_2(t_k{-}\tau, x_k-y)dy \\[4pt] & -\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\omega (\underline{V}+1)}{(\overline{U}+\omega )(\underline{U}+\omega )} W_1(t_k{-}\tau, x_k-y)dy \\[4pt] \leq & (\delta +d_m)W_1(t_k,x_k)-\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\left [\frac{\tilde{u}_+}{\tilde{u}_++\omega } +\frac{\tilde{v}_+}{\omega }\right ]W(t_k)dy \\[4pt] \leq & (\delta +d_m)W_1(t_k,x_k)-\frac{\alpha e^{-d_i\tau }\tilde{v}_+}{\omega }W(t_k) \end{align*}
\begin{align*} 0\leq & \frac{\partial W_1(t_k,x_k)}{\partial t}+d_m W_1(t_k,x_k) \\[4pt] & -\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\overline{U}(t_k{-}\tau, x_k-y)}{\overline{U}(t_k{-}\tau, x_k-y)+\omega }(\overline{V}(t_k{-}\tau, x_k-y)+1)dy \\[4pt] & +\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\underline{U}(t_k{-}\tau, x_k-y)}{\underline{U}(t_k{-}\tau, x_k-y)+\omega }(\underline{V}(t_k{-}\tau, x_k-y)+1)dy \\[4pt] \leq & (\delta +d_m)W_1(t_k,x_k)-\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\overline{U}}{\overline{U}+\omega }W_2(t_k{-}\tau, x_k-y)dy \\[4pt] & -\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\omega (\underline{V}+1)}{(\overline{U}+\omega )(\underline{U}+\omega )} W_1(t_k{-}\tau, x_k-y)dy \\[4pt] \leq & (\delta +d_m)W_1(t_k,x_k)-\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\left [\frac{\tilde{u}_+}{\tilde{u}_++\omega } +\frac{\tilde{v}_+}{\omega }\right ]W(t_k)dy \\[4pt] \leq & (\delta +d_m)W_1(t_k,x_k)-\frac{\alpha e^{-d_i\tau }\tilde{v}_+}{\omega }W(t_k) \end{align*}
and
 \begin{align*} 0 \leq & \frac{\partial W_2(t_k,x_k)}{\partial t} -D\int _{\mathbb{R}}J(y)[W_2(t_k,x_k-y)-W_2(t_k,x_k)]dy\\[4pt] &+(1+\overline{V}+\underline{V})W_2(t_k,x_k) -d\int _{\mathbb{R}}k(y)\frac{\overline{U}(t_k, x_k-y)}{\overline{U}(t_k, x_k-y)+\omega }(\overline{V}(t_k, x_k-y)+1)dy \\[4pt] & +d\int _{\mathbb{R}}k(y)\frac{\underline{U}(t_k, x_k-y)}{\underline{U}(t_k, x_k-y)+\omega }(\underline{V}(t_k, x_k-y)+1)dy \\[4pt] \leq & (\delta +1+\overline{V}+\underline{V})W_2(t_k,x_k) \\[4pt] & -d\int _{\mathbb{R}}k(y)\left [\frac{\overline{U}}{\overline{U}+\omega }W_2(t_k, x_k-y)-\frac{\omega (\underline{V}+1)}{(\overline{U}+\omega )(\underline{U}+\omega )} W_1(t_k, x_k-y)\right ] dy \\[4pt] \leq & (\delta +1+\overline{V}+\underline{V})W_2(t_k,x_k)-d\int _{\mathbb{R}}k(y)\left [\frac{\tilde{u}_+}{\tilde{u}_++\omega } +\frac{\tilde{v}_+}{\omega }\right ]W(t_k)dy \\[4pt] \leq & (\delta +1+\overline{V}+\underline{V})W_2(t_k,x_k)-\frac{d\tilde{v}_+}{\omega }W(t_k). \end{align*}
\begin{align*} 0 \leq & \frac{\partial W_2(t_k,x_k)}{\partial t} -D\int _{\mathbb{R}}J(y)[W_2(t_k,x_k-y)-W_2(t_k,x_k)]dy\\[4pt] &+(1+\overline{V}+\underline{V})W_2(t_k,x_k) -d\int _{\mathbb{R}}k(y)\frac{\overline{U}(t_k, x_k-y)}{\overline{U}(t_k, x_k-y)+\omega }(\overline{V}(t_k, x_k-y)+1)dy \\[4pt] & +d\int _{\mathbb{R}}k(y)\frac{\underline{U}(t_k, x_k-y)}{\underline{U}(t_k, x_k-y)+\omega }(\underline{V}(t_k, x_k-y)+1)dy \\[4pt] \leq & (\delta +1+\overline{V}+\underline{V})W_2(t_k,x_k) \\[4pt] & -d\int _{\mathbb{R}}k(y)\left [\frac{\overline{U}}{\overline{U}+\omega }W_2(t_k, x_k-y)-\frac{\omega (\underline{V}+1)}{(\overline{U}+\omega )(\underline{U}+\omega )} W_1(t_k, x_k-y)\right ] dy \\[4pt] \leq & (\delta +1+\overline{V}+\underline{V})W_2(t_k,x_k)-d\int _{\mathbb{R}}k(y)\left [\frac{\tilde{u}_+}{\tilde{u}_++\omega } +\frac{\tilde{v}_+}{\omega }\right ]W(t_k)dy \\[4pt] \leq & (\delta +1+\overline{V}+\underline{V})W_2(t_k,x_k)-\frac{d\tilde{v}_+}{\omega }W(t_k). \end{align*}
Letting
![]() $k\rightarrow \infty$
, we have that
$k\rightarrow \infty$
, we have that
![]() $\left(\delta +d_m-\frac{\alpha e^{-d_i\tau }\tilde{v}_+}{\omega }\right)W(t_0)\ge 0$
or
$\left(\delta +d_m-\frac{\alpha e^{-d_i\tau }\tilde{v}_+}{\omega }\right)W(t_0)\ge 0$
or
![]() $\left(\delta +1-\frac{d\tilde{v}_+}{\omega }\right)W(t_0)\ge 0$
, which imply that
$\left(\delta +1-\frac{d\tilde{v}_+}{\omega }\right)W(t_0)\ge 0$
, which imply that
![]() $W(t_0)\ge 0$
by choosing
$W(t_0)\ge 0$
by choosing
![]() $\delta \gt \max \{-d_m+\frac{\alpha e^{-d_i\tau }\tilde{v}_+}{\omega }, -1+\frac{d\tilde{v}_+}{\omega }\}$
. It contradicts to
$\delta \gt \max \{-d_m+\frac{\alpha e^{-d_i\tau }\tilde{v}_+}{\omega }, -1+\frac{d\tilde{v}_+}{\omega }\}$
. It contradicts to
![]() $W(t_0)\lt 0$
. The proof is complete.
$W(t_0)\lt 0$
. The proof is complete.
Proposition 2.4.
For any
![]() $\phi \in \mathcal{C}_{\mathbf{K}}$
with
$\phi \in \mathcal{C}_{\mathbf{K}}$
with
![]() $\phi \not \equiv 0$
, let
$\phi \not \equiv 0$
, let
![]() $(U(t,x;\,\phi ),V(t,x;\,\phi ))$
be the solution of (2.3). Then, there exists
$(U(t,x;\,\phi ),V(t,x;\,\phi ))$
be the solution of (2.3). Then, there exists
![]() $t_1=t_1(\phi )\gt 0$
such that
$t_1=t_1(\phi )\gt 0$
such that
![]() $U(t,x;\,\phi )\gt 0$
and
$U(t,x;\,\phi )\gt 0$
and
![]() $V(t,x;\,\phi )\gt 0$
for any
$V(t,x;\,\phi )\gt 0$
for any
![]() $t\gt t_1(\phi )$
,
$t\gt t_1(\phi )$
,
![]() $x\in \mathbb{R}$
.
$x\in \mathbb{R}$
.
Proof. In view of Lemma 2.1, when
![]() $\phi \,:\!= (\phi _1,\phi _2)\in \mathcal{C}_{\mathbf{K}}$
,
$\phi \,:\!= (\phi _1,\phi _2)\in \mathcal{C}_{\mathbf{K}}$
,
![]() $(U,V)(t,x)\in [0,\tilde u_+]\times [0,\tilde v_+]$
for
$(U,V)(t,x)\in [0,\tilde u_+]\times [0,\tilde v_+]$
for
![]() $(t,x)\in (0,{+}\infty )\times \mathbb{R}$
. Then, it is easy to see that
$(t,x)\in (0,{+}\infty )\times \mathbb{R}$
. Then, it is easy to see that
 \begin{align} \begin{cases} \displaystyle\frac{\partial V}{\partial t}=(J\ast V-V)-V(1+V)+d\int _{\mathbb{R}}k(x-y)\frac{U(t,y)}{U(t,y)+\omega }(V(t, y)+1)dy\\[6pt] \quad\displaystyle \ \ \ \ \ge (J\ast V-V)-V(1+\tilde v_+),\\[6pt] \displaystyle V(0,x)=\phi _2(0,x), \ \ \ \ x\in \mathbb{R}. \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle\frac{\partial V}{\partial t}=(J\ast V-V)-V(1+V)+d\int _{\mathbb{R}}k(x-y)\frac{U(t,y)}{U(t,y)+\omega }(V(t, y)+1)dy\\[6pt] \quad\displaystyle \ \ \ \ \ge (J\ast V-V)-V(1+\tilde v_+),\\[6pt] \displaystyle V(0,x)=\phi _2(0,x), \ \ \ \ x\in \mathbb{R}. \end{cases} \end{align}
By the strong maximum principle (see e.g. [Reference Li, Sun and Wang17, Theorem 2.1]), we obtain that
![]() $V(t,x)\gt 0$
for
$V(t,x)\gt 0$
for
![]() $(t,x)\in (0,{+}\infty )\times \mathbb{R}$
, if
$(t,x)\in (0,{+}\infty )\times \mathbb{R}$
, if
![]() $\phi _2(0,x)\ge ({\not}{\equiv}) 0$
for
$\phi _2(0,x)\ge ({\not}{\equiv}) 0$
for
![]() $x\in \mathbb{R}$
.
$x\in \mathbb{R}$
.
Next, we show that there exists
![]() $t_0\in [0,\tau ]$
such that
$t_0\in [0,\tau ]$
such that
![]() $U(t_0,x)\not \equiv 0$
for all
$U(t_0,x)\not \equiv 0$
for all
![]() $x\in \mathbb{R}$
, which means there exists some
$x\in \mathbb{R}$
, which means there exists some
![]() $x$
such that
$x$
such that
![]() $U(t_0,x)\gt 0$
. Assume, by contradiction, that
$U(t_0,x)\gt 0$
. Assume, by contradiction, that
![]() $U(t,x)\equiv 0$
for all
$U(t,x)\equiv 0$
for all
![]() $t$
and
$t$
and
![]() $x$
. It then follows from the first equation in (2.5) that
$x$
. It then follows from the first equation in (2.5) that
![]() $\phi _1(t,x)\equiv 0$
for
$\phi _1(t,x)\equiv 0$
for
![]() $t\in [{-}\tau,0]$
and
$t\in [{-}\tau,0]$
and
![]() $x\in \mathbb{R}$
, which is a contradiction. Since
$x\in \mathbb{R}$
, which is a contradiction. Since
![]() $U_t\gt -d_mU$
, we obtain that for
$U_t\gt -d_mU$
, we obtain that for
![]() $t\in [t_0,t_0+\tau ]$
,
$t\in [t_0,t_0+\tau ]$
,
![]() $U(t,x)\not \equiv 0$
for all
$U(t,x)\not \equiv 0$
for all
![]() $x\in \mathbb{R}$
. Thus, by the first equation of (2.3), we get
$x\in \mathbb{R}$
. Thus, by the first equation of (2.3), we get
Let
![]() $t_1(\phi )=t_0+\tau$
. Then by (2.8), we obtain that
$t_1(\phi )=t_0+\tau$
. Then by (2.8), we obtain that
![]() $U(t,x)\gt 0$
for
$U(t,x)\gt 0$
for
![]() $t\gt t_1(\phi )$
,
$t\gt t_1(\phi )$
,
![]() $x\in \mathbb{R}$
. The proof is complete.
$x\in \mathbb{R}$
. The proof is complete.
3. Spreading speeds
3.1. Existence of spreading speed
In this subsection, we are devoted to establishing that the solution of (2.3) has a spreading speed.
Definition 3.1.
A family of mappings
![]() $\{Q_t\}_{t\ge 0}$
is said to be a semiflow on
$\{Q_t\}_{t\ge 0}$
is said to be a semiflow on
![]() $\mathcal{C}_{\mathbf{K}}$
, if the following three properties hold: (i)
$\mathcal{C}_{\mathbf{K}}$
, if the following three properties hold: (i)
![]() $Q_0=I$
, where I is the identity mapping; (ii)
$Q_0=I$
, where I is the identity mapping; (ii)
![]() $Q_t\circ Q_s=Q_{t+s}$
for all
$Q_t\circ Q_s=Q_{t+s}$
for all
![]() $t, s\gt 0$
; (iii)
$t, s\gt 0$
; (iii)
![]() $Q_{t}[\phi ](x)$
is continuous in
$Q_{t}[\phi ](x)$
is continuous in
![]() $(t,\phi )\in (0,{+}\infty )\times \mathcal{C}_{\mathbf{K}}$
.
$(t,\phi )\in (0,{+}\infty )\times \mathcal{C}_{\mathbf{K}}$
.
For any
![]() $u=(u_1(\theta, x), u_2(\theta,x))\in \mathcal{C}$
, define the reflection operator
$u=(u_1(\theta, x), u_2(\theta,x))\in \mathcal{C}$
, define the reflection operator
![]() $\mathcal{R}$
by
$\mathcal{R}$
by
Given
![]() $y\in \mathbb{R}$
, define the translation operator
$y\in \mathbb{R}$
, define the translation operator
![]() $T_y$
by
$T_y$
by
A set
![]() $W\subseteq \mathcal{C}$
is said to be
$W\subseteq \mathcal{C}$
is said to be
![]() $T$
-invariant if
$T$
-invariant if
![]() $T_y[W]=W$
for any
$T_y[W]=W$
for any
![]() $y\in \mathbb{R}$
. For a given operator
$y\in \mathbb{R}$
. For a given operator
![]() $Q\,{:}\,\mathcal{C}_{\mathbf{K}}\rightarrow \mathcal{C}_{\mathbf{K}}$
, we make the following assumptions:
$Q\,{:}\,\mathcal{C}_{\mathbf{K}}\rightarrow \mathcal{C}_{\mathbf{K}}$
, we make the following assumptions:
-
(A1)
 $Q[\mathcal{R}[u]]=\mathcal{R}[Q[u]]$
,
$Q[\mathcal{R}[u]]=\mathcal{R}[Q[u]]$
,
 $T_{y}[Q[u]]=Q[T_{y}[u]]$
,
$T_{y}[Q[u]]=Q[T_{y}[u]]$
,
 $\forall y\in \mathbb{R}$
.
$\forall y\in \mathbb{R}$
. -
(A2)
 $Q\,{:}\,\mathcal{C}_{\mathbf{K}}\rightarrow \mathcal{C}_{\mathbf{K}}$
is continuous with respect to the compact open topology.
$Q\,{:}\,\mathcal{C}_{\mathbf{K}}\rightarrow \mathcal{C}_{\mathbf{K}}$
is continuous with respect to the compact open topology. -
(A3) One of the following two properties holds:
-
(a)
 $\{Q[u](\cdot,x):u\in \mathcal{C}_{\mathbf{K}}, x\in \mathbb{R}\}$
is precompact in
$\{Q[u](\cdot,x):u\in \mathcal{C}_{\mathbf{K}}, x\in \mathbb{R}\}$
is precompact in
 $\bar{\mathcal{C}}_{\mathbf{K}}$
.
$\bar{\mathcal{C}}_{\mathbf{K}}$
. -
(b)
 $Q[\mathcal{C}_{\mathbf{K}}](0,\cdot )$
is precompact in
$Q[\mathcal{C}_{\mathbf{K}}](0,\cdot )$
is precompact in
 $X$
, and there is a positive number
$X$
, and there is a positive number
 $\varsigma \leq \tau$
such that
$\varsigma \leq \tau$
such that
 $Q[u](\theta,x)=u(\theta +\varsigma,x)$
for
$Q[u](\theta,x)=u(\theta +\varsigma,x)$
for
 ${-}\tau \leq \theta \leq -\varsigma$
, and the operator(3.1)has the property that
${-}\tau \leq \theta \leq -\varsigma$
, and the operator(3.1)has the property that \begin{align} S[u](\theta,x)= \begin{cases} \displaystyle u(0,x), \ \ \ \ \ \ \ {-}\tau \leq \theta \leq -\varsigma, \\[6pt] \displaystyle Q[u](\theta,x), \ \ -\varsigma \leq \theta \leq 0, \end{cases} \end{align}
\begin{align} S[u](\theta,x)= \begin{cases} \displaystyle u(0,x), \ \ \ \ \ \ \ {-}\tau \leq \theta \leq -\varsigma, \\[6pt] \displaystyle Q[u](\theta,x), \ \ -\varsigma \leq \theta \leq 0, \end{cases} \end{align}
 $S[\Pi ](\cdot,0)\,:\!=\{S[u](\theta,0)\,{:}\,u\in \Pi \}$
is precompact in
$S[\Pi ](\cdot,0)\,:\!=\{S[u](\theta,0)\,{:}\,u\in \Pi \}$
is precompact in
 $\bar{\mathcal{C}}_{\mathbf{K}}$
for any
$\bar{\mathcal{C}}_{\mathbf{K}}$
for any
 $T$
-invariant set
$T$
-invariant set
 $\Pi \subset \mathcal{C}_{\mathbf{K}}$
with
$\Pi \subset \mathcal{C}_{\mathbf{K}}$
with
 $\Pi (0,\cdot )\,:\!=\{u(0,x)\,{:}\,u\in \Pi \}$
precompact in
$\Pi (0,\cdot )\,:\!=\{u(0,x)\,{:}\,u\in \Pi \}$
precompact in
 $X$
.
$X$
.
-
-
(A4)
 $Q\,{:}\,\mathcal{C}_{\mathbf{K}}\rightarrow \mathcal{C}_{\mathbf{K}}$
is monotone in the sense that
$Q\,{:}\,\mathcal{C}_{\mathbf{K}}\rightarrow \mathcal{C}_{\mathbf{K}}$
is monotone in the sense that
 $Q[u]\geq Q(v)$
whenever
$Q[u]\geq Q(v)$
whenever
 $u\geq v$
in
$u\geq v$
in
 $\mathcal{C}_{\mathbf{K}}$
.
$\mathcal{C}_{\mathbf{K}}$
. -
(A5)
 $Q\,{:}\,\bar{\mathcal{C}}_{\mathbf{K}}\rightarrow \bar{\mathcal{C}}_{\mathbf{K}}$
admits exactly two fixed points
$Q\,{:}\,\bar{\mathcal{C}}_{\mathbf{K}}\rightarrow \bar{\mathcal{C}}_{\mathbf{K}}$
admits exactly two fixed points
 $\mathbf{0}$
and
$\mathbf{0}$
and
 $\mathbf{K}$
, and for any positive number
$\mathbf{K}$
, and for any positive number
 $\epsilon$
, there is a
$\epsilon$
, there is a
 $\zeta \in \bar{\mathcal{C}}_{\mathbf{K}}$
with
$\zeta \in \bar{\mathcal{C}}_{\mathbf{K}}$
with
 $\|\zeta \|\lt \epsilon$
such that
$\|\zeta \|\lt \epsilon$
such that
 $Q[\zeta ]\gg \zeta$
, where
$Q[\zeta ]\gg \zeta$
, where
 $\|\cdot \|$
is the maximum norm in
$\|\cdot \|$
is the maximum norm in
 $\bar{\mathcal{C}}$
.
$\bar{\mathcal{C}}$
.
Let
![]() $Q_t$
be the solution map of (2.3), that is,
$Q_t$
be the solution map of (2.3), that is,
In order to apply the theory in [Reference Liang and Zhao20] to address the existence of a spreading speed for (2.3), we need to verify that the solution map
![]() $Q_t$
defined in (3.2) satisfies the above properties (A1)–(A5). It is straightforward to verify that (A1) holds, since
$Q_t$
defined in (3.2) satisfies the above properties (A1)–(A5). It is straightforward to verify that (A1) holds, since
![]() $(U(t,{-}x),V(t,{-}x))$
and
$(U(t,{-}x),V(t,{-}x))$
and
![]() $(U(t,x-y),V(t,x-y))$
are also solution of (2.1) provided that
$(U(t,x-y),V(t,x-y))$
are also solution of (2.1) provided that
![]() $(U(t,x),V(t,x))$
is a solution (2.1) and
$(U(t,x),V(t,x))$
is a solution (2.1) and
![]() $y\in \mathbb{R}$
.
$y\in \mathbb{R}$
.
Lemma 3.2.
Let
![]() $Q_t$
be the solution map of (2.3) defined in (3.2). Then,
$Q_t$
be the solution map of (2.3) defined in (3.2). Then,
![]() $\{Q_t\}_{t\geq 0}$
is a semiflow on
$\{Q_t\}_{t\geq 0}$
is a semiflow on
![]() $\mathcal{C}_{\mathbf{K}}$
.
$\mathcal{C}_{\mathbf{K}}$
.
Proof. We shall prove that
![]() $Q_t$
is the continuous in
$Q_t$
is the continuous in
![]() $\phi$
with respect to the compact open topology uniformly for
$\phi$
with respect to the compact open topology uniformly for
![]() $t\in [0,t_0]$
with
$t\in [0,t_0]$
with
![]() $t_0\gt 0$
. In view of [Reference Weng and Zhao29, Lemma 3.1], the solution semigroup of the following linear nonlocal dispersal equation
$t_0\gt 0$
. In view of [Reference Weng and Zhao29, Lemma 3.1], the solution semigroup of the following linear nonlocal dispersal equation
 \begin{align} \begin{cases} \displaystyle \frac{\partial V(t,x)}{\partial t}=D(J\ast V-V)(t,x), \ \ t\gt 0, \ x\in \mathbb{R} \\[6pt] \displaystyle V(0,x)=\psi (x), \ \ \ x\in \mathbb{R}, \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle \frac{\partial V(t,x)}{\partial t}=D(J\ast V-V)(t,x), \ \ t\gt 0, \ x\in \mathbb{R} \\[6pt] \displaystyle V(0,x)=\psi (x), \ \ \ x\in \mathbb{R}, \end{cases} \end{align}
is given by
for any
![]() $\psi \in \mathbb{Y}$
, where
$\psi \in \mathbb{Y}$
, where
![]() $\mathbb{Y}$
is the set of all bounded and continuous functions from
$\mathbb{Y}$
is the set of all bounded and continuous functions from
![]() $\mathbb{R}$
to
$\mathbb{R}$
to
![]() $\mathbb{R}$
, and
$\mathbb{R}$
, and
For any
![]() $\psi \in \mathbb{Y}$
, define
$\psi \in \mathbb{Y}$
, define
![]() $\|\cdot \|=\sup _{x\in \mathbb{R}}|\psi (x)|$
. It is easy to see that
$\|\cdot \|=\sup _{x\in \mathbb{R}}|\psi (x)|$
. It is easy to see that
![]() $\|a_0(\psi )\|=\|\psi \|$
,
$\|a_0(\psi )\|=\|\psi \|$
,
![]() $\|a_1(\psi )(x)\|=\|\int _{\mathbb{R}}J(x-y)a_{0}(\psi )(y)dy\|\le \|\psi \|$
. By induction, we can obtain
$\|a_1(\psi )(x)\|=\|\int _{\mathbb{R}}J(x-y)a_{0}(\psi )(y)dy\|\le \|\psi \|$
. By induction, we can obtain
![]() $\|a_k(\psi )(x)\|\le \|\psi \|$
for all
$\|a_k(\psi )(x)\|\le \|\psi \|$
for all
![]() $k=0,1,2,\cdots$
. By (3.4), we have
$k=0,1,2,\cdots$
. By (3.4), we have
It is clear that the system (2.3) can be rewritten into the following integral system
 \begin{align} \begin{cases} \displaystyle U(t,x)= e^{-d_mt}\phi _1(0,x) +\int _0^te^{-d_m(t-s)}\mathcal{H}_1[U,V](s,x)ds, \\[6pt] \displaystyle V(t,x)= P(t)\phi _2(0,x) +\int _0^t P(t-s)\mathcal{H}_2[U,V](s,x)ds, \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle U(t,x)= e^{-d_mt}\phi _1(0,x) +\int _0^te^{-d_m(t-s)}\mathcal{H}_1[U,V](s,x)ds, \\[6pt] \displaystyle V(t,x)= P(t)\phi _2(0,x) +\int _0^t P(t-s)\mathcal{H}_2[U,V](s,x)ds, \end{cases} \end{align}
where
 \begin{align} \begin{cases} \displaystyle \mathcal{H}_1[U,V](t,x) \,:\!=\alpha e^{-d_i\tau } \int _{\mathbb{R}}k(y)\frac{U(t{-}\tau,x-y)}{U(t{-}\tau,x-y)+\omega }(V(t{-}\tau,x-y)+1)dy,\\[6pt] \displaystyle \mathcal{H}_2[U,V](t,x)\,:\!=-V(1+V)+d\int _{\mathbb{R}}k(y)\frac{U(t,x-y)}{U(t,x-y)+\omega }(V(t,x-y)+1)dy. \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle \mathcal{H}_1[U,V](t,x) \,:\!=\alpha e^{-d_i\tau } \int _{\mathbb{R}}k(y)\frac{U(t{-}\tau,x-y)}{U(t{-}\tau,x-y)+\omega }(V(t{-}\tau,x-y)+1)dy,\\[6pt] \displaystyle \mathcal{H}_2[U,V](t,x)\,:\!=-V(1+V)+d\int _{\mathbb{R}}k(y)\frac{U(t,x-y)}{U(t,x-y)+\omega }(V(t,x-y)+1)dy. \end{cases} \end{align}
For
![]() $\phi ^1=(\phi _1^1,\phi ^1_2)$
,
$\phi ^1=(\phi _1^1,\phi ^1_2)$
,
![]() $\phi ^2=(\phi _1^2,\phi _2^2)$
$\phi ^2=(\phi _1^2,\phi _2^2)$
![]() $\in \mathcal{C}_{\mathbf{K}}$
, we define
$\in \mathcal{C}_{\mathbf{K}}$
, we define
where
Choose
![]() $t_0\gt 0$
and for any
$t_0\gt 0$
and for any
![]() $\varepsilon \gt 0$
, we let
$\varepsilon \gt 0$
, we let
It is easy to see that there exists
![]() $(t^*,x^*)\in [{-}\tau,t]\times \mathbb{R}$
such that
$(t^*,x^*)\in [{-}\tau,t]\times \mathbb{R}$
such that
for
![]() $(s,\theta,x)\in [0,t]\times [{-}\tau,0]\times \mathbb{R}$
with
$(s,\theta,x)\in [0,t]\times [{-}\tau,0]\times \mathbb{R}$
with
![]() $t\in [0,t_0]$
. Set
$t\in [0,t_0]$
. Set
with
Then, there exists
![]() $M=M(t_0,\varepsilon )$
such that
$M=M(t_0,\varepsilon )$
such that
for
![]() $0\leq s\leq t$
. Hence, for above
$0\leq s\leq t$
. Hence, for above
![]() $\varepsilon \gt 0$
, choose
$\varepsilon \gt 0$
, choose
![]() $\delta =\displaystyle\frac{\varepsilon }{8}e^{-\sigma t_{0}}$
such that when
$\delta =\displaystyle\frac{\varepsilon }{8}e^{-\sigma t_{0}}$
such that when
![]() $\|\phi ^1-\phi ^2\|_{\Sigma _M(x^*)}\lt \delta$
, by (3.5) and (3.6), we obtain
$\|\phi ^1-\phi ^2\|_{\Sigma _M(x^*)}\lt \delta$
, by (3.5) and (3.6), we obtain
 \begin{align*} & \|w_t(\theta,x)\|_{\Sigma _M(x^*)} \\ &\quad\leq w^1(t^*,x^*)+w^2(t^*,x^*)+\frac{\varepsilon }{4}e^{-\sigma t_{0}} \\ &\quad\leq e^{-d_mt}w^1(0,x^*)+w^2(0,x^*)+\frac{\varepsilon }{4}e^{-\sigma t_{0}} \\ &\qquad +\alpha e^{-d_i\tau }\int _0^{t^*}\int _{\mathbb{R}}e^{-d_m(t^*-s)}k(y)\left [\frac{v_+}{\omega }w^1(s{-}\tau,x^*-y) +w^2(s{-}\tau,x^*-y)\right ] dyds \\ &\qquad +\int _0^{t^*}(2v_+-1)w^2(s,x^*)ds+d\int _0^{t^*}\int _{\mathbb{R}}k(y)\left [\frac{v_+}{\omega }w^1(s,x^*-y) +w^2(s,x^*-y)\right ] dyds \\ &\quad\leq 2\|\phi ^1-\phi ^2\|_{\Sigma _M(x^*)}+\frac{\varepsilon }{4}e^{-\sigma t_{0}}+(2v_+-1)\int _0^{t}(\|w_s\|_{\Sigma _M(x^*)}+\varepsilon _1)ds \\ & \qquad +\frac{(\alpha e ^{-d_i\tau }+d)(v_++\omega )}{\omega }\int _0^{t}(\|w_s\|_{\Sigma _M(x^*)}+\varepsilon _1)ds \\ &\quad\leq 2\delta +\frac{\varepsilon }{4}e^{-\sigma t_{0}}+\varepsilon _1\sigma t+\sigma \int _0^{t}\|w_s\|_{\Sigma _M(x^*)}ds. \end{align*}
\begin{align*} & \|w_t(\theta,x)\|_{\Sigma _M(x^*)} \\ &\quad\leq w^1(t^*,x^*)+w^2(t^*,x^*)+\frac{\varepsilon }{4}e^{-\sigma t_{0}} \\ &\quad\leq e^{-d_mt}w^1(0,x^*)+w^2(0,x^*)+\frac{\varepsilon }{4}e^{-\sigma t_{0}} \\ &\qquad +\alpha e^{-d_i\tau }\int _0^{t^*}\int _{\mathbb{R}}e^{-d_m(t^*-s)}k(y)\left [\frac{v_+}{\omega }w^1(s{-}\tau,x^*-y) +w^2(s{-}\tau,x^*-y)\right ] dyds \\ &\qquad +\int _0^{t^*}(2v_+-1)w^2(s,x^*)ds+d\int _0^{t^*}\int _{\mathbb{R}}k(y)\left [\frac{v_+}{\omega }w^1(s,x^*-y) +w^2(s,x^*-y)\right ] dyds \\ &\quad\leq 2\|\phi ^1-\phi ^2\|_{\Sigma _M(x^*)}+\frac{\varepsilon }{4}e^{-\sigma t_{0}}+(2v_+-1)\int _0^{t}(\|w_s\|_{\Sigma _M(x^*)}+\varepsilon _1)ds \\ & \qquad +\frac{(\alpha e ^{-d_i\tau }+d)(v_++\omega )}{\omega }\int _0^{t}(\|w_s\|_{\Sigma _M(x^*)}+\varepsilon _1)ds \\ &\quad\leq 2\delta +\frac{\varepsilon }{4}e^{-\sigma t_{0}}+\varepsilon _1\sigma t+\sigma \int _0^{t}\|w_s\|_{\Sigma _M(x^*)}ds. \end{align*}
By Gronwall’s inequality, we further have
This shows that
![]() $Q_t$
is continuous in
$Q_t$
is continuous in
![]() $\phi$
with respect to compact open topology uniformly for
$\phi$
with respect to compact open topology uniformly for
![]() $t\in [0,t_0]$
, which, together with the continuity of
$t\in [0,t_0]$
, which, together with the continuity of
![]() $Q_t$
in
$Q_t$
in
![]() $t$
from Lemma 2.1, implies that
$t$
from Lemma 2.1, implies that
![]() $Q_t$
is continuous in
$Q_t$
is continuous in
![]() $(t,\phi )$
with respect to the compact open topology. The proof is complete.
$(t,\phi )$
with respect to the compact open topology. The proof is complete.
By Lemma 3.2, the property (A2) holds. The property (A4) can be guaranteed by Lemma 2.3. It is easy to verify that the property (A5) also holds, see also [Reference Wang, Liu, Shi and Martinez27, Lemma 3.7]. We just need to prove that the solution map
![]() $Q_t$
satisfies the property (A3).
$Q_t$
satisfies the property (A3).
Lemma 3.3.
![]() $Q_t$
satisfies (A3)(a) if
$Q_t$
satisfies (A3)(a) if
![]() $t\ge \tau$
and satisfies (A3)(b) if
$t\ge \tau$
and satisfies (A3)(b) if
![]() $t\lt \tau$
.
$t\lt \tau$
.
Proof. In view of Lemma 2.1, when
![]() $\phi \in \mathcal{C}_{\mathbf{K}}$
, the solution
$\phi \in \mathcal{C}_{\mathbf{K}}$
, the solution
![]() $(U(t,x;\,\phi ),V(t,x;\,\phi ))$
of (2.3) is bounded. More precisely,
$(U(t,x;\,\phi ),V(t,x;\,\phi ))$
of (2.3) is bounded. More precisely,
![]() $\mathbf{0}\leq (U(t,x;\,\phi ),V(t,x;\,\phi )) \leq \mathbf{K}, \ \forall \ t\geq 0, \ x\in \mathbb{R}$
. It then follows from the first equation of (2.3) that
$\mathbf{0}\leq (U(t,x;\,\phi ),V(t,x;\,\phi )) \leq \mathbf{K}, \ \forall \ t\geq 0, \ x\in \mathbb{R}$
. It then follows from the first equation of (2.3) that
 \begin{align*} |U_t(t,x;\,\phi )|\le & d_m|U|+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\left |\frac{U(t{-}\tau,y;\,\phi )}{U(t{-}\tau,y;\,\phi )+\omega }\right ||V(t{-}\tau, y;\,\phi )+1|dy\\ \le & d_m \tilde u_++\alpha e^{-d_i\tau }\frac{\tilde u_+}{\omega }(\tilde v_++1)=\!:\,L, \end{align*}
\begin{align*} |U_t(t,x;\,\phi )|\le & d_m|U|+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(x-y)\left |\frac{U(t{-}\tau,y;\,\phi )}{U(t{-}\tau,y;\,\phi )+\omega }\right ||V(t{-}\tau, y;\,\phi )+1|dy\\ \le & d_m \tilde u_++\alpha e^{-d_i\tau }\frac{\tilde u_+}{\omega }(\tilde v_++1)=\!:\,L, \end{align*}
which means that
![]() $U_t$
is bounded for
$U_t$
is bounded for
![]() $t\geq 0$
. Let
$t\geq 0$
. Let
![]() $[a,b]\subseteq \mathbb{R}$
with
$[a,b]\subseteq \mathbb{R}$
with
![]() $a\gt 0$
be any bounded interval,
$a\gt 0$
be any bounded interval,
![]() $I\subseteq \mathbb{R}$
be a compact interval and
$I\subseteq \mathbb{R}$
be a compact interval and
![]() $\tilde K=\min \{K\in \mathbb{N}\,{:}\,I\subseteq [{-}K,K]\}$
. Then for any
$\tilde K=\min \{K\in \mathbb{N}\,{:}\,I\subseteq [{-}K,K]\}$
. Then for any
![]() $t_1, t_2\in [a, b]$
and
$t_1, t_2\in [a, b]$
and
![]() $x\in I$
, one has
$x\in I$
, one has
Hence, for any
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $\delta =\frac{\varepsilon }{L}$
, such that for any
$\delta =\frac{\varepsilon }{L}$
, such that for any
![]() $\phi \in \mathcal{C}_{\mathbf{K}}$
, any
$\phi \in \mathcal{C}_{\mathbf{K}}$
, any
![]() $x\in I$
,
$x\in I$
,
![]() $s_1, s_2\in [{-}\tau,0]$
with
$s_1, s_2\in [{-}\tau,0]$
with
![]() $|s_1-s_2|\lt \delta$
, we obtain
$|s_1-s_2|\lt \delta$
, we obtain
where
![]() $t_0\gt \tau$
, which implies that
$t_0\gt \tau$
, which implies that
![]() $\{Q_t^1[\phi ](s,x)\,{:}\,\phi \in \mathcal{C}_{\mathbf{K}}, x\in \mathbb{R}\}$
is a family of equicontinuous functions of
$\{Q_t^1[\phi ](s,x)\,{:}\,\phi \in \mathcal{C}_{\mathbf{K}}, x\in \mathbb{R}\}$
is a family of equicontinuous functions of
![]() $s\in [{-}\tau,0]$
. By the Arzela-Ascoli Theorem, we obtain that
$s\in [{-}\tau,0]$
. By the Arzela-Ascoli Theorem, we obtain that
![]() $\{Q_t^1[\phi ](\cdot,x)\,{:}\,\phi \in \mathcal{C}_{\mathbf{K}}, x\in \mathbb{R}\}$
is precompact in
$\{Q_t^1[\phi ](\cdot,x)\,{:}\,\phi \in \mathcal{C}_{\mathbf{K}}, x\in \mathbb{R}\}$
is precompact in
![]() $C([{-}\tau,0],\mathbb{R})$
if
$C([{-}\tau,0],\mathbb{R})$
if
![]() $t\geq \tau$
. Thus,
$t\geq \tau$
. Thus,
![]() $Q_t^1$
satisfies (A3)(a) for
$Q_t^1$
satisfies (A3)(a) for
![]() $t\geq \tau$
. On the other hand, if
$t\geq \tau$
. On the other hand, if
![]() $t\lt \tau$
, we set
$t\lt \tau$
, we set
![]() $\varsigma\,{=}\,1$
. Then, for the
$\varsigma\,{=}\,1$
. Then, for the
![]() $T$
-invariant set
$T$
-invariant set
![]() $\Pi$
defined in (A3), the set
$\Pi$
defined in (A3), the set
![]() $\{S^1[\Pi ](\theta,0)\,{:}\,\theta \in [{-}\varsigma,0]\}$
is precompact in
$\{S^1[\Pi ](\theta,0)\,{:}\,\theta \in [{-}\varsigma,0]\}$
is precompact in
![]() $C([{-}\varsigma,0],\mathbb{R})$
, where
$C([{-}\varsigma,0],\mathbb{R})$
, where
![]() $S^1$
is the first component of the operator
$S^1$
is the first component of the operator
![]() $S$
defined in (3.1). It is clear that
$S$
defined in (3.1). It is clear that
![]() $\{S^1[\Pi ](\theta,0)\,{:}\,\theta \in [{-}\tau,{-}\varsigma ]\}$
is an infinite set of constant functions in
$\{S^1[\Pi ](\theta,0)\,{:}\,\theta \in [{-}\tau,{-}\varsigma ]\}$
is an infinite set of constant functions in
![]() $C([{-}\tau,-\varsigma ],\mathbb{R})$
, and hence, it is precompact in
$C([{-}\tau,-\varsigma ],\mathbb{R})$
, and hence, it is precompact in
![]() $C([{-}\tau,-\varsigma ],\mathbb{R})$
. Therefore,
$C([{-}\tau,-\varsigma ],\mathbb{R})$
. Therefore,
![]() $Q_t^1$
satisfies (A3)(b) for
$Q_t^1$
satisfies (A3)(b) for
![]() $t\lt \tau$
.
$t\lt \tau$
.
Now we prove that
![]() $Q^2_t$
satisfies (A3). By the second equation of (2.3), we have
$Q^2_t$
satisfies (A3). By the second equation of (2.3), we have
By a similar argument as that for
![]() $Q^1_t$
, we obtain that
$Q^1_t$
, we obtain that
![]() $\{Q_t^2[\phi ](\cdot,x)\,{:}\,\phi \in \mathcal{C}_{\mathbf{K}}, x\in \mathbb{R}\}$
is precompact in
$\{Q_t^2[\phi ](\cdot,x)\,{:}\,\phi \in \mathcal{C}_{\mathbf{K}}, x\in \mathbb{R}\}$
is precompact in
![]() $C([{-}\tau,0],\mathbb{R})$
if
$C([{-}\tau,0],\mathbb{R})$
if
![]() $t\geq \tau$
. Thus,
$t\geq \tau$
. Thus,
![]() $Q_t^2$
satisfies (A3)(a) for
$Q_t^2$
satisfies (A3)(a) for
![]() $t\geq \tau$
. In the following, we verify that
$t\geq \tau$
. In the following, we verify that
![]() $Q_t^2$
satisfies (A3)(b) when
$Q_t^2$
satisfies (A3)(b) when
![]() $t\in [0,\tau ]$
. For any
$t\in [0,\tau ]$
. For any
![]() $\phi \in \mathcal{C}_{\mathbf{K}}$
, we fix
$\phi \in \mathcal{C}_{\mathbf{K}}$
, we fix
![]() $\tilde t\in (0,\tau ]$
and define
$\tilde t\in (0,\tau ]$
and define
 \begin{align*} S^2[\phi ](\theta,x)= \begin{cases} \phi _2(0,x), \ \ \ \ \ \ \ {-}\tau \leq \theta \leq -\tilde t, \\ Q^2_{\tilde t}[\phi ](\theta,x), \ \ {-}\tilde t\leq \theta \leq 0. \end{cases} \end{align*}
\begin{align*} S^2[\phi ](\theta,x)= \begin{cases} \phi _2(0,x), \ \ \ \ \ \ \ {-}\tau \leq \theta \leq -\tilde t, \\ Q^2_{\tilde t}[\phi ](\theta,x), \ \ {-}\tilde t\leq \theta \leq 0. \end{cases} \end{align*}
Let
![]() $\Pi \subset \mathcal{C}_{\mathbf{K}}$
be a
$\Pi \subset \mathcal{C}_{\mathbf{K}}$
be a
![]() $T$
-invariant set with
$T$
-invariant set with
![]() $\Pi (0,\cdot )\,:\!=\{u(0,x)\,{:}\,u\in \Pi \}$
precompact in
$\Pi (0,\cdot )\,:\!=\{u(0,x)\,{:}\,u\in \Pi \}$
precompact in
![]() $X$
. We just need to show that for any given compact interval
$X$
. We just need to show that for any given compact interval
![]() $I\in \mathbb{R}$
,
$I\in \mathbb{R}$
,
![]() $S^2(\Pi )$
is equicontinuous on
$S^2(\Pi )$
is equicontinuous on
![]() $[{-}\tau,0]\times I$
.
$[{-}\tau,0]\times I$
.
When
![]() $(s,x)\in [{-}\tau,{-}\tilde t]\times I$
, one has
$(s,x)\in [{-}\tau,{-}\tilde t]\times I$
, one has
![]() $S^2[\phi ](s,x)=\phi _2(0,x)$
for all
$S^2[\phi ](s,x)=\phi _2(0,x)$
for all
![]() $\phi \in \Pi$
. Hence, by the precompactness of
$\phi \in \Pi$
. Hence, by the precompactness of
![]() $\Pi (0,\cdot )$
in
$\Pi (0,\cdot )$
in
![]() $X$
, we obtain that
$X$
, we obtain that
![]() $S^2(\Pi )$
is equicontinuous on
$S^2(\Pi )$
is equicontinuous on
![]() $[{-}\tau,{-}\tilde t]\times I$
.
$[{-}\tau,{-}\tilde t]\times I$
.
Since
![]() $P(t)$
is uniformly continuous for
$P(t)$
is uniformly continuous for
![]() $t$
in a bounded interval in the compact open topology with respect to the initial value, one can show that
$t$
in a bounded interval in the compact open topology with respect to the initial value, one can show that
is bounded in
![]() $X_+$
, where
$X_+$
, where
![]() $\mathcal{H}_2$
is defined in (3.7). Then there exists
$\mathcal{H}_2$
is defined in (3.7). Then there exists
![]() $M\gt 0$
such that
$M\gt 0$
such that
where the norm
with
![]() $|\cdot |$
is the usual norm in
$|\cdot |$
is the usual norm in
![]() $\mathbb{R}$
. Thus, we derive that
$\mathbb{R}$
. Thus, we derive that
![]() $\sup _{|x|\le \tilde K}|P(t-s)\mathcal{H}_2[\phi ](x)|\le 2^{\tilde K}M$
. Hence, for any
$\sup _{|x|\le \tilde K}|P(t-s)\mathcal{H}_2[\phi ](x)|\le 2^{\tilde K}M$
. Hence, for any
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $\delta _1=\min \{\frac{\varepsilon }{2^{\tilde K}4M},\tilde t\}$
, such that for any
$\delta _1=\min \{\frac{\varepsilon }{2^{\tilde K}4M},\tilde t\}$
, such that for any
![]() $t\le \delta _1$
,
$t\le \delta _1$
,
![]() $x\in I$
and
$x\in I$
and
![]() $\phi \in \Pi$
, we have
$\phi \in \Pi$
, we have
In [Reference Ignat and Rossi14, Section 2], Ignat and Rossi showed that the solution of (3.3) can also be written as
![]() $V(t,x)=[P(t)\psi ](x)=\int _{\mathbb{R}}G(t,y)\psi (x-y)dy$
, where
$V(t,x)=[P(t)\psi ](x)=\int _{\mathbb{R}}G(t,y)\psi (x-y)dy$
, where
![]() $G(t,x)=e^{-Dt}\delta _0(x)+R(t,x)$
,
$G(t,x)=e^{-Dt}\delta _0(x)+R(t,x)$
,
![]() $\delta _0(x)$
is the delta measure at zero and
$\delta _0(x)$
is the delta measure at zero and
![]() $R(t,x)=\frac{1}{2\pi }\int _{\mathbb{R}}(e^{D(\hat J(\xi )-1)t}-e^{-Dt})e^{jx\xi }d\xi$
with
$R(t,x)=\frac{1}{2\pi }\int _{\mathbb{R}}(e^{D(\hat J(\xi )-1)t}-e^{-Dt})e^{jx\xi }d\xi$
with
![]() $j=\sqrt{-1}$
and
$j=\sqrt{-1}$
and
![]() $\hat J$
being the Fourier transform of
$\hat J$
being the Fourier transform of
![]() $J$
. Moreover, it is proved that
$J$
. Moreover, it is proved that
![]() $|G(t,\cdot )|_{L^1(\mathbb{R})}\le 3$
for any
$|G(t,\cdot )|_{L^1(\mathbb{R})}\le 3$
for any
![]() $t\gt 0$
. Since
$t\gt 0$
. Since
![]() $(\phi _1,\phi _2)\in \Pi (0, \cdot )$
and
$(\phi _1,\phi _2)\in \Pi (0, \cdot )$
and
![]() $\Pi (0,\cdot )$
is precompact in
$\Pi (0,\cdot )$
is precompact in
![]() $X$
, then for the above
$X$
, then for the above
![]() $I$
, there exists
$I$
, there exists
![]() $\delta _2\gt 0$
such that for any
$\delta _2\gt 0$
such that for any
![]() $x_1, x_2\in I$
satisfying
$x_1, x_2\in I$
satisfying
![]() $|x_1 {-}x_2|\lt \delta _2$
, we have
$|x_1 {-}x_2|\lt \delta _2$
, we have
![]() $|\phi _2(x_1)-\phi _2(x_2)]\lt \frac{\varepsilon }{12}$
, and hence,
$|\phi _2(x_1)-\phi _2(x_2)]\lt \frac{\varepsilon }{12}$
, and hence,
 \begin{align} \left |P(t)[\phi _2](x_1)-P(t)[\phi _2](x_2)\right |=&\left |\int _{\mathbb{R}}G(t,y)[\phi _2(x_1-y)-\phi _2(x_2-y)]dy\right |\notag \\ \le &\int _{\mathbb{R}}|G(t,y)||\phi _2(x_1-y)-\phi _2(x_2-y)|dy\notag \\ \le &\|G(t,\cdot )\|_{L^1(\mathbb{R})}\frac{\varepsilon }{12}\le \frac{\varepsilon }{4},\ \forall t\in [0,\delta _1]. \end{align}
\begin{align} \left |P(t)[\phi _2](x_1)-P(t)[\phi _2](x_2)\right |=&\left |\int _{\mathbb{R}}G(t,y)[\phi _2(x_1-y)-\phi _2(x_2-y)]dy\right |\notag \\ \le &\int _{\mathbb{R}}|G(t,y)||\phi _2(x_1-y)-\phi _2(x_2-y)|dy\notag \\ \le &\|G(t,\cdot )\|_{L^1(\mathbb{R})}\frac{\varepsilon }{12}\le \frac{\varepsilon }{4},\ \forall t\in [0,\delta _1]. \end{align}
On the other hand, for all
![]() $t \gt 0$
,
$t \gt 0$
,
![]() $x \in \mathbb{R}$
and
$x \in \mathbb{R}$
and
![]() $\phi \in \mathcal{C}_{\mathbf{K}}$
, we have
$\phi \in \mathcal{C}_{\mathbf{K}}$
, we have
![]() $|[P(t)\phi _2](x)|\le \tilde v_+$
. It is easy to see that
$|[P(t)\phi _2](x)|\le \tilde v_+$
. It is easy to see that
Hence, for
![]() $t_1, t_2\in [0,\delta _1]$
,
$t_1, t_2\in [0,\delta _1]$
,
![]() $(\phi _1, \phi _2)\in \Pi (0, \cdot )$
, there exists
$(\phi _1, \phi _2)\in \Pi (0, \cdot )$
, there exists
![]() $\delta _3\,:\!=\displaystyle\frac{\varepsilon }{8D\tilde v_+}$
such that when
$\delta _3\,:\!=\displaystyle\frac{\varepsilon }{8D\tilde v_+}$
such that when
![]() $|t_1-t_2|\le \delta _3$
, we derive
$|t_1-t_2|\le \delta _3$
, we derive
Combining (3.8)–(3.10), when
![]() $s_1, s_2\in [{-}\tilde t, \delta _1{-}\tilde t]$
and
$s_1, s_2\in [{-}\tilde t, \delta _1{-}\tilde t]$
and
![]() $x_1, x_2\in I$
satisfying
$x_1, x_2\in I$
satisfying
![]() $|s_1-s_2|\lt \delta _3$
and
$|s_1-s_2|\lt \delta _3$
and
![]() $|x_1-x_2|\lt \delta _2$
, for any
$|x_1-x_2|\lt \delta _2$
, for any
![]() $\phi \in \Pi (0, \cdot )$
, we obtain
$\phi \in \Pi (0, \cdot )$
, we obtain
 \begin{align*} &|S^2(\phi )(s_1,x_2)-S^2(\phi )(s_2,x_2)|=|Q_{\tilde t}^2[\phi ](s_1,x_1)-Q_{\tilde t}^2[\phi ](s_2,x_2)|\\ &\quad=|V(\tilde t+s_1,x_1;\,\phi )-V(\tilde t+s_2,x_2;\,\phi )|\\ &\quad\le |P(\tilde t+s_1)[\phi _2](x_1)-P(\tilde t+s_2)[\phi _2](x_2)|\\ &\qquad +\left |\int _0^{\tilde t+s_1} P(\tilde t+s_1-s)\mathcal{H}_2[U,V](s,x_1)ds-\int _0^{\tilde t+s_2} P(\tilde t+s_2-s)\mathcal{H}_2[U,V](s,x_2)ds\right |\\ &\quad\le |P(\tilde t+s_1)[\phi _2](x_1)-P(\tilde t+s_1)[\phi _2](x_2)|+|P(\tilde t+s_1)[\phi _2](x_2)-P(\tilde t+s_2)[\phi _2](x_2)|\\ &\qquad +\left |\int _0^{\tilde t+s_1} P(\tilde t+s_1-s)\mathcal{H}_2[U,V](s,x_1)ds\right |+\left |\int _0^{\tilde t+s_2} P(\tilde t+s_2-s)\mathcal{H}_2[U,V](s,x_2)ds\right |\\ &\quad\lt \varepsilon, \end{align*}
\begin{align*} &|S^2(\phi )(s_1,x_2)-S^2(\phi )(s_2,x_2)|=|Q_{\tilde t}^2[\phi ](s_1,x_1)-Q_{\tilde t}^2[\phi ](s_2,x_2)|\\ &\quad=|V(\tilde t+s_1,x_1;\,\phi )-V(\tilde t+s_2,x_2;\,\phi )|\\ &\quad\le |P(\tilde t+s_1)[\phi _2](x_1)-P(\tilde t+s_2)[\phi _2](x_2)|\\ &\qquad +\left |\int _0^{\tilde t+s_1} P(\tilde t+s_1-s)\mathcal{H}_2[U,V](s,x_1)ds-\int _0^{\tilde t+s_2} P(\tilde t+s_2-s)\mathcal{H}_2[U,V](s,x_2)ds\right |\\ &\quad\le |P(\tilde t+s_1)[\phi _2](x_1)-P(\tilde t+s_1)[\phi _2](x_2)|+|P(\tilde t+s_1)[\phi _2](x_2)-P(\tilde t+s_2)[\phi _2](x_2)|\\ &\qquad +\left |\int _0^{\tilde t+s_1} P(\tilde t+s_1-s)\mathcal{H}_2[U,V](s,x_1)ds\right |+\left |\int _0^{\tilde t+s_2} P(\tilde t+s_2-s)\mathcal{H}_2[U,V](s,x_2)ds\right |\\ &\quad\lt \varepsilon, \end{align*}
which means
![]() $S^2(\Pi )$
is equicontinuous on
$S^2(\Pi )$
is equicontinuous on
![]() $[{-}\tilde t,\delta _1{-}\tilde t]\times I$
.
$[{-}\tilde t,\delta _1{-}\tilde t]\times I$
.
Finally, we need to verify that
![]() $S^2(\Pi )$
is equicontinuous on
$S^2(\Pi )$
is equicontinuous on
![]() $[\delta _1 {-}\tilde t, 0]\times I$
. Note that if
$[\delta _1 {-}\tilde t, 0]\times I$
. Note that if
![]() $s\in [\delta _1 {-}\tilde t, 0]$
, then
$s\in [\delta _1 {-}\tilde t, 0]$
, then
![]() $\tilde t+ s \in [\delta _1, \tilde t]$
. Thus, we can prove the current case similar to that for (A3)(a). Therefore,
$\tilde t+ s \in [\delta _1, \tilde t]$
. Thus, we can prove the current case similar to that for (A3)(a). Therefore,
![]() $S^2(\Pi )$
is equicontinuous on
$S^2(\Pi )$
is equicontinuous on
![]() $[{-}\tau,0]\times I$
. The proof is complete.
$[{-}\tau,0]\times I$
. The proof is complete.
Now we are ready to apply the general theory in [Reference Liang and Zhao20, Theorem 2.17] to show that the map
![]() $Q_t$
admits a spreading speed
$Q_t$
admits a spreading speed
![]() $c^*$
, which is also the spreading speed of solutions to (2.3).
$c^*$
, which is also the spreading speed of solutions to (2.3).
Theorem 3.4.
Assume that (H1) and (H2) hold. Then, there exists a spreading speed
![]() $c^*$
of
$c^*$
of
![]() $Q_t$
in the following sense.
$Q_t$
in the following sense.
-
(i) For any
 $c\gt c^*$
, if
$c\gt c^*$
, if
 $\phi \in \mathcal{C}_{\mathbf{K}}$
with
$\phi \in \mathcal{C}_{\mathbf{K}}$
with
 $\mathbf{0}\ll \phi \ll \mathbf{K}$
and
$\mathbf{0}\ll \phi \ll \mathbf{K}$
and
 $\phi (\cdot,x)=0$
for
$\phi (\cdot,x)=0$
for
 $x$
outside a bounded interval, then
$x$
outside a bounded interval, then
 \begin{equation*}\lim _{t\rightarrow \infty,|x|\geq ct}U(t,x;\,\phi )=\lim _{t\rightarrow \infty,|x|\geq ct}V(t,x;\,\phi )=0.\end{equation*}
\begin{equation*}\lim _{t\rightarrow \infty,|x|\geq ct}U(t,x;\,\phi )=\lim _{t\rightarrow \infty,|x|\geq ct}V(t,x;\,\phi )=0.\end{equation*}
-
(ii) For any
 $c\lt c^*$
and any
$c\lt c^*$
and any
 $\sigma \in \bar{\mathcal{C}}_{\mathbf{K}}$
with
$\sigma \in \bar{\mathcal{C}}_{\mathbf{K}}$
with
 $\sigma \gg 0$
, there exists a positive number
$\sigma \gg 0$
, there exists a positive number
 $r_\sigma$
such that if
$r_\sigma$
such that if
 $\phi \in \mathcal{C}_{\mathbf{K}}$
and
$\phi \in \mathcal{C}_{\mathbf{K}}$
and
 $\phi \gg \sigma$
for
$\phi \gg \sigma$
for
 $x$
on an interval of length
$x$
on an interval of length
 $2r_\sigma$
, then
$2r_\sigma$
, then
 \begin{equation*}\lim _{t\rightarrow \infty,|x|\leq ct}U(t,x;\,\phi )=\tilde u_+ \ \ \ \text{and} \ \ \ \lim _{t\rightarrow \infty,|x|\leq ct}V(t,x;\,\phi )=\tilde v_+.\end{equation*}
\begin{equation*}\lim _{t\rightarrow \infty,|x|\leq ct}U(t,x;\,\phi )=\tilde u_+ \ \ \ \text{and} \ \ \ \lim _{t\rightarrow \infty,|x|\leq ct}V(t,x;\,\phi )=\tilde v_+.\end{equation*}
3.2. Estimates of spreading speed
In this subsection, we study the upper and lower bounds of the spreading speed established in Section 3.1. We first give an estimate of the upper bound of the spreading speed
![]() $c^*$
. Consider the following linear system
$c^*$
. Consider the following linear system
 \begin{equation} \begin{cases} \displaystyle \frac{\partial U}{\partial t}&=-d_m U+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\left [\frac{1}{\omega }U(t{-}\tau,x-y)+\frac{\tilde{u}_+}{\tilde{u}_++\omega }V(t{-}\tau,x-y)\right ] dy, \\[6pt] \displaystyle \frac{\partial V}{\partial t}&=D\int _{\mathbb{R}}J(y)[V(t,x-y)-V(x,t)]dy -V \\[6pt] & \displaystyle\quad+d\int _{\mathbb{R}}k(y)\left [\frac{1}{\omega }U(t,x-y)+\frac{\tilde{u}_+}{\tilde{u}_++\omega }V(t,x-y)\right ] dy, \end{cases} \end{equation}
\begin{equation} \begin{cases} \displaystyle \frac{\partial U}{\partial t}&=-d_m U+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\left [\frac{1}{\omega }U(t{-}\tau,x-y)+\frac{\tilde{u}_+}{\tilde{u}_++\omega }V(t{-}\tau,x-y)\right ] dy, \\[6pt] \displaystyle \frac{\partial V}{\partial t}&=D\int _{\mathbb{R}}J(y)[V(t,x-y)-V(x,t)]dy -V \\[6pt] & \displaystyle\quad+d\int _{\mathbb{R}}k(y)\left [\frac{1}{\omega }U(t,x-y)+\frac{\tilde{u}_+}{\tilde{u}_++\omega }V(t,x-y)\right ] dy, \end{cases} \end{equation}
where
![]() $t\gt 0$
,
$t\gt 0$
,
![]() $x\in \mathbb{R}$
. For any
$x\in \mathbb{R}$
. For any
![]() $\mu \in \mathbb{R}_+$
, define
$\mu \in \mathbb{R}_+$
, define
![]() $U(t,x)=e^{-\mu x}\eta _1(t)$
and
$U(t,x)=e^{-\mu x}\eta _1(t)$
and
![]() $V(t,x)=e^{-\mu x}\eta _2(t)$
. Then, it is easy to see that
$V(t,x)=e^{-\mu x}\eta _2(t)$
. Then, it is easy to see that
![]() $\eta =(\eta _1,\eta _2)$
satisfies
$\eta =(\eta _1,\eta _2)$
satisfies
where
 \begin{align*} M =\left ( \begin{array}{cc} -d_m & 0 \\ \frac{d\tilde{k}(\mu )}{\omega } & D\tilde{J}(\mu )-D-1+\frac{d\tilde{u}_+\tilde{k}(\mu )}{\tilde{u}_++\omega } \end{array} \right ) \end{align*}
\begin{align*} M =\left ( \begin{array}{cc} -d_m & 0 \\ \frac{d\tilde{k}(\mu )}{\omega } & D\tilde{J}(\mu )-D-1+\frac{d\tilde{u}_+\tilde{k}(\mu )}{\tilde{u}_++\omega } \end{array} \right ) \end{align*}
and
 \begin{align*} B =\left ( \begin{array}{cc} \frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega } & \frac{\alpha e^{-d_i\tau }\tilde{u}_{+}\tilde{k}(\mu )}{\tilde{u}_++\omega } \\ 0 & 0 \end{array} \right ), \end{align*}
\begin{align*} B =\left ( \begin{array}{cc} \frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega } & \frac{\alpha e^{-d_i\tau }\tilde{u}_{+}\tilde{k}(\mu )}{\tilde{u}_++\omega } \\ 0 & 0 \end{array} \right ), \end{align*}
where
![]() $\tilde{k}(\mu )=\int _{\mathbb{R}}k(y)e^{\mu y}dy\lt \infty$
and
$\tilde{k}(\mu )=\int _{\mathbb{R}}k(y)e^{\mu y}dy\lt \infty$
and
![]() $\tilde{J}(\mu )=\int _{\mathbb{R}}J(y)e^{\mu y}dy\lt \infty$
for any
$\tilde{J}(\mu )=\int _{\mathbb{R}}J(y)e^{\mu y}dy\lt \infty$
for any
![]() $\mu \gt 0$
. It is clear that if
$\mu \gt 0$
. It is clear that if
![]() $\eta (t)$
is a solution of (3.12), then
$\eta (t)$
is a solution of (3.12), then
![]() $e^{-\mu x}\eta (t)$
is a solution of (3.11). Define
$e^{-\mu x}\eta (t)$
is a solution of (3.11). Define
here
![]() $N_t$
is the solution operator of (3.11), and
$N_t$
is the solution operator of (3.11), and
![]() $\eta (t,\eta ^0)$
is the solution of (3.12) with
$\eta (t,\eta ^0)$
is the solution of (3.12) with
![]() $\eta ^0=\eta (\theta )$
for
$\eta ^0=\eta (\theta )$
for
![]() $\theta \in [{-}\tau,0]$
. Since system (3.12) is cooperative and irreducible, by [Reference Smith25, Theorem 5.1], we obtain that the characteristic equation
$\theta \in [{-}\tau,0]$
. Since system (3.12) is cooperative and irreducible, by [Reference Smith25, Theorem 5.1], we obtain that the characteristic equation
has a real root
![]() $\lambda (\mu )\gt 0$
, and the real parts of all other roots are less than
$\lambda (\mu )\gt 0$
, and the real parts of all other roots are less than
![]() $\lambda (\mu )$
. Let
$\lambda (\mu )$
. Let
![]() $\zeta =(\zeta _1(\theta ),\zeta _2(\theta ))$
be the eigenfunction of the infinitesimal generator corresponding to
$\zeta =(\zeta _1(\theta ),\zeta _2(\theta ))$
be the eigenfunction of the infinitesimal generator corresponding to
![]() $\lambda (\mu )$
. In fact,
$\lambda (\mu )$
. In fact,
![]() $\zeta$
can take the form
$\zeta$
can take the form
![]() $(\zeta _1(\theta ),\zeta _2(\theta ))=(\zeta _{10}e^{\lambda (\mu )\theta },\zeta _{20}e^{\lambda (\mu )\theta })$
with
$(\zeta _1(\theta ),\zeta _2(\theta ))=(\zeta _{10}e^{\lambda (\mu )\theta },\zeta _{20}e^{\lambda (\mu )\theta })$
with
![]() $\zeta _{10},\zeta _{20}\gt 0$
,
$\zeta _{10},\zeta _{20}\gt 0$
,
![]() $\theta \in [{-}\tau,0]$
. Then,
$\theta \in [{-}\tau,0]$
. Then,
![]() $e^{\lambda (\mu )t}$
is the principle eigenvalue of
$e^{\lambda (\mu )t}$
is the principle eigenvalue of
![]() $\mathcal{B}_\mu ^t$
with eigenfunction
$\mathcal{B}_\mu ^t$
with eigenfunction
![]() $\zeta$
. In particular,
$\zeta$
. In particular,
![]() $\gamma (\mu )\,:\!=e^{\lambda (\mu )}$
is the eigenvalue of
$\gamma (\mu )\,:\!=e^{\lambda (\mu )}$
is the eigenvalue of
![]() $\mathcal{B}_\mu ^1$
. Define
$\mathcal{B}_\mu ^1$
. Define
By using [Reference Liang and Zhao20, Lemma 3.8], we can easily obtain the following properties of
![]() $\Phi (\mu )$
.
$\Phi (\mu )$
.
Lemma 3.5. The statements are valid:
-
(i)
 $\Phi (\mu )\rightarrow \infty$
as
$\Phi (\mu )\rightarrow \infty$
as
 $\mu \rightarrow 0^+$
;
$\mu \rightarrow 0^+$
; -
(ii)
 $\Phi (\mu )$
is strictly decreasing for
$\Phi (\mu )$
is strictly decreasing for
 $\mu$
near
$\mu$
near
 $0$
;
$0$
; -
(iii)
 $\Phi '(\mu )$
changes sign at most once on
$\Phi '(\mu )$
changes sign at most once on
 $(0,\infty)$
;
$(0,\infty)$
; -
(iv)
 $\lim \limits _{\mu \rightarrow \infty }\Phi (\mu )$
exists, where the limit may be infinite.
$\lim \limits _{\mu \rightarrow \infty }\Phi (\mu )$
exists, where the limit may be infinite.
Then, we can get an estimate of an upper bound of the spreading speed
![]() $c^*$
.
$c^*$
.
Proposition 3.6.
Let
![]() $c^*$
be the spreading speed of
$c^*$
be the spreading speed of
![]() $Q_t$
defined as in Theorem 3.4, and let
$Q_t$
defined as in Theorem 3.4, and let
![]() $\lambda (\mu )$
and
$\lambda (\mu )$
and
![]() $\Phi (\mu )$
be defined as above. Then,
$\Phi (\mu )$
be defined as above. Then,
Proof. Clearly, the solution
![]() $(U(t,x),V(t,x))$
of (2.1) is a lower solution of (3.11), and hence,
$(U(t,x),V(t,x))$
of (2.1) is a lower solution of (3.11), and hence,
![]() $Q_1(\phi )\leq N_1(\phi )$
for any
$Q_1(\phi )\leq N_1(\phi )$
for any
![]() $\phi \in \mathcal{C}_{\mathbf{K}}$
. It is easy to verify that
$\phi \in \mathcal{C}_{\mathbf{K}}$
. It is easy to verify that
![]() $N_1$
and
$N_1$
and
![]() $\mathcal{B}_\mu ^1$
satisfies (C1)–(C6) in [Reference Liang and Zhao20]. By [Reference Liang and Zhao20, Theorem 3.10], it suffices to show that the principal eigenvalue
$\mathcal{B}_\mu ^1$
satisfies (C1)–(C6) in [Reference Liang and Zhao20]. By [Reference Liang and Zhao20, Theorem 3.10], it suffices to show that the principal eigenvalue
![]() $\gamma (0)$
is greater than
$\gamma (0)$
is greater than
![]() $1$
, and the infimum of
$1$
, and the infimum of
![]() $\Phi (\mu )$
is attained at some
$\Phi (\mu )$
is attained at some
![]() $\mu ^*\gt 0$
.
$\mu ^*\gt 0$
.
When
![]() $\mu =0$
, it follows from (3.13) that
$\mu =0$
, it follows from (3.13) that
 \begin{align*} \mathcal{P}(\lambda ) & =\left (\lambda +d_m-\frac{\alpha e^{-d_i\tau }}{\omega }e^{-\lambda \tau }\right )\left (\lambda +1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\right ) -\frac{d\alpha e^{-d_i\tau }\tilde{u}_+}{\omega (\tilde{u}_++\omega )}e^{-\lambda \tau } \\ & =\lambda ^2+\left (d_m+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\right )\lambda +\left (1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\right )d_m -\frac{\alpha e^{-d_i\tau }}{\omega }(\lambda +1)e^{-\lambda \tau }=0. \end{align*}
\begin{align*} \mathcal{P}(\lambda ) & =\left (\lambda +d_m-\frac{\alpha e^{-d_i\tau }}{\omega }e^{-\lambda \tau }\right )\left (\lambda +1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\right ) -\frac{d\alpha e^{-d_i\tau }\tilde{u}_+}{\omega (\tilde{u}_++\omega )}e^{-\lambda \tau } \\ & =\lambda ^2+\left (d_m+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\right )\lambda +\left (1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\right )d_m -\frac{\alpha e^{-d_i\tau }}{\omega }(\lambda +1)e^{-\lambda \tau }=0. \end{align*}
Let
 \begin{align*} & f_1(\lambda )=\lambda ^2+\left (d_m+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\right )\lambda +\left (1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\right )d_m, \\ & f_2(\lambda,\tau )=\frac{\alpha e^{-d_i\tau }}{\omega }(\lambda +1)e^{-\lambda \tau }. \end{align*}
\begin{align*} & f_1(\lambda )=\lambda ^2+\left (d_m+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\right )\lambda +\left (1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\right )d_m, \\ & f_2(\lambda,\tau )=\frac{\alpha e^{-d_i\tau }}{\omega }(\lambda +1)e^{-\lambda \tau }. \end{align*}
Since
![]() $d_m\lt \tilde{d}_m\,:\!=\frac{\alpha e^{-d_i\tau }}{\omega }$
by (H2), we obtain
$d_m\lt \tilde{d}_m\,:\!=\frac{\alpha e^{-d_i\tau }}{\omega }$
by (H2), we obtain
It is easy to see that
![]() $\frac{\partial f _2(\lambda, \tau )}{\partial \lambda }=\frac{\alpha e^{-d_i\tau }}{\omega }e^{-\lambda \tau }(1{-}\tau (\lambda +1))$
. Hence, if
$\frac{\partial f _2(\lambda, \tau )}{\partial \lambda }=\frac{\alpha e^{-d_i\tau }}{\omega }e^{-\lambda \tau }(1{-}\tau (\lambda +1))$
. Hence, if
![]() $\tau \geq 1$
, then
$\tau \geq 1$
, then
![]() $\frac{\partial f _2(\lambda, \tau )}{\partial \lambda }\leq 0$
for
$\frac{\partial f _2(\lambda, \tau )}{\partial \lambda }\leq 0$
for
![]() $\lambda \geq 0$
. If
$\lambda \geq 0$
. If
![]() $\tau \lt 1$
, then
$\tau \lt 1$
, then
![]() $f_2(\lambda,\tau )$
reaches its unique local (thus global) maximum at
$f_2(\lambda,\tau )$
reaches its unique local (thus global) maximum at
![]() $\lambda =\frac{1}{\tau }-1$
and tends to
$\lambda =\frac{1}{\tau }-1$
and tends to
![]() $0$
as
$0$
as
![]() $\lambda \rightarrow {+}\infty$
. Moreover,
$\lambda \rightarrow {+}\infty$
. Moreover,
![]() $f_1(\lambda )$
is convex for
$f_1(\lambda )$
is convex for
![]() $\lambda \gt 0$
, while for any fixed
$\lambda \gt 0$
, while for any fixed
![]() $\tau \gt 0$
,
$\tau \gt 0$
,
![]() $f_2(\lambda,\tau )$
has at most one reflection point for
$f_2(\lambda,\tau )$
has at most one reflection point for
![]() $\lambda \gt 0$
. Hence, there is a unique
$\lambda \gt 0$
. Hence, there is a unique
![]() $\lambda ^*\gt 0$
such that
$\lambda ^*\gt 0$
such that
![]() $f_1(\lambda ^*)=f_2(\lambda ^*,\tau )$
no matter what value
$f_1(\lambda ^*)=f_2(\lambda ^*,\tau )$
no matter what value
![]() $\tau$
takes. This implies that
$\tau$
takes. This implies that
![]() $\lambda (0)=\lambda ^*\gt 0$
, and hence,
$\lambda (0)=\lambda ^*\gt 0$
, and hence,
![]() $\gamma (0)=e^{\lambda (0)}\gt 1$
, i.e. the condition (C7) in [Reference Liang and Zhao20] is satisfied.
$\gamma (0)=e^{\lambda (0)}\gt 1$
, i.e. the condition (C7) in [Reference Liang and Zhao20] is satisfied.
We now prove that
![]() $\Phi (\mu )$
attains its infimum at some
$\Phi (\mu )$
attains its infimum at some
![]() $\mu ^*\gt 0$
, which can be obtained by proving that
$\mu ^*\gt 0$
, which can be obtained by proving that
![]() $\lim \limits _{\mu \rightarrow {+}\infty }\Phi (\mu )={+}\infty$
. By (3.13), we have
$\lim \limits _{\mu \rightarrow {+}\infty }\Phi (\mu )={+}\infty$
. By (3.13), we have
 \begin{align} \mathcal{P}(\lambda ) = &\lambda ^2+\left (d_m-D\tilde{J}(\mu )+D+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\tilde{k}(\mu )\right )\lambda \notag \\ & +\left (-D\tilde{J}(\mu )+D+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\tilde{k}(\mu )\right )d_m \notag \\ & -\frac{\alpha e^{-d_i\tau }}{\omega }\tilde{k}(\mu )(\lambda -D\tilde{J}(\mu )+D+1)e^{-\lambda \tau } = 0. \end{align}
\begin{align} \mathcal{P}(\lambda ) = &\lambda ^2+\left (d_m-D\tilde{J}(\mu )+D+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\tilde{k}(\mu )\right )\lambda \notag \\ & +\left (-D\tilde{J}(\mu )+D+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\tilde{k}(\mu )\right )d_m \notag \\ & -\frac{\alpha e^{-d_i\tau }}{\omega }\tilde{k}(\mu )(\lambda -D\tilde{J}(\mu )+D+1)e^{-\lambda \tau } = 0. \end{align}
Let
 \begin{align*} f_3(\lambda )&= \lambda ^2+\left (d_m-D\tilde{J}(\mu )+D+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\tilde{k}(\mu )\right )\lambda \\[2pt] &\quad +\left (-D\tilde{J}(\mu )+D+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\tilde{k}(\mu )\right )d_m, \\[2pt] f_4(\lambda,\tau )&=\frac{\alpha e^{-d_i\tau }}{\omega }\tilde{k}(\mu )(\lambda -D\tilde{J}(\mu )+D+1)e^{-\lambda \tau }. \end{align*}
\begin{align*} f_3(\lambda )&= \lambda ^2+\left (d_m-D\tilde{J}(\mu )+D+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\tilde{k}(\mu )\right )\lambda \\[2pt] &\quad +\left (-D\tilde{J}(\mu )+D+1-\frac{d\tilde{u}_+}{\tilde{u}_++\omega }\tilde{k}(\mu )\right )d_m, \\[2pt] f_4(\lambda,\tau )&=\frac{\alpha e^{-d_i\tau }}{\omega }\tilde{k}(\mu )(\lambda -D\tilde{J}(\mu )+D+1)e^{-\lambda \tau }. \end{align*}
It is easy to compute that
![]() $\tilde J'(\mu )\gt 0$
for
$\tilde J'(\mu )\gt 0$
for
![]() $\mu \gt 0$
and
$\mu \gt 0$
and
![]() $\lim _{\mu \rightarrow {+}\infty }\tilde J(\mu )={+}\infty$
. Hence, for any large
$\lim _{\mu \rightarrow {+}\infty }\tilde J(\mu )={+}\infty$
. Hence, for any large
![]() $\mu$
, we have
$\mu$
, we have
 \begin{align*} &f_3\left(D\tilde{J}(\mu )-D-1+\frac{1}{\tau }\right)\lt 0,\\ &f^{\prime}_3(\lambda )\gt 0,\quad \forall \lambda \gt D\tilde{J}(\mu )-D-1+\frac{1}{\tau },\\ &\lim \limits _{\lambda \rightarrow {+}\infty }f_3(\lambda )={+}\infty, \end{align*}
\begin{align*} &f_3\left(D\tilde{J}(\mu )-D-1+\frac{1}{\tau }\right)\lt 0,\\ &f^{\prime}_3(\lambda )\gt 0,\quad \forall \lambda \gt D\tilde{J}(\mu )-D-1+\frac{1}{\tau },\\ &\lim \limits _{\lambda \rightarrow {+}\infty }f_3(\lambda )={+}\infty, \end{align*}
and
 \begin{align*} &f_4\left(D\tilde{J}(\mu )-D-1+\frac{1}{\tau },\tau \right)\gt 0,\\ &\frac{\partial f_4(\lambda,\tau )}{\partial \lambda }\lt 0,\quad \forall \lambda \gt D\tilde{J}(\mu )-D-1+\frac{1}{\tau },\\ &\lim \limits _{\lambda \rightarrow {+}\infty }f_4(\lambda,\tau )=0. \end{align*}
\begin{align*} &f_4\left(D\tilde{J}(\mu )-D-1+\frac{1}{\tau },\tau \right)\gt 0,\\ &\frac{\partial f_4(\lambda,\tau )}{\partial \lambda }\lt 0,\quad \forall \lambda \gt D\tilde{J}(\mu )-D-1+\frac{1}{\tau },\\ &\lim \limits _{\lambda \rightarrow {+}\infty }f_4(\lambda,\tau )=0. \end{align*}
Thus, (3.14) has a unique positive root
![]() $\lambda (\mu )\gt D\tilde{J}(\mu )-D-1+\frac{1}{\tau }$
. Hence,
$\lambda (\mu )\gt D\tilde{J}(\mu )-D-1+\frac{1}{\tau }$
. Hence,
The proof is complete.
Next, we provide an estimate of the lower bound of the spreading speed
![]() $c^*$
.
$c^*$
.
Proposition 3.7.
Let
![]() $c^*$
be the spreading speed of
$c^*$
be the spreading speed of
![]() $Q_t$
defined as in Theorem 3.4. Then,
$Q_t$
defined as in Theorem 3.4. Then,
Here,
![]() $\Lambda (\mu )=\max \{D\tilde{J}(\mu )-D-1,\Lambda _2(\mu )\}$
, where
$\Lambda (\mu )=\max \{D\tilde{J}(\mu )-D-1,\Lambda _2(\mu )\}$
, where
![]() $\Lambda _2(\mu )$
is the unique positive root of
$\Lambda _2(\mu )$
is the unique positive root of
![]() $\mathcal{L}(\Lambda,\mu )\,:\!=\Lambda +d_m-\frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega }e^{-\Lambda \tau }=0.$
$\mathcal{L}(\Lambda,\mu )\,:\!=\Lambda +d_m-\frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega }e^{-\Lambda \tau }=0.$
Proof. Choose any small
![]() $\varepsilon \gt 0$
. Let
$\varepsilon \gt 0$
. Let
![]() $P^\varepsilon _t$
be the solution operator of the following linear system:
$P^\varepsilon _t$
be the solution operator of the following linear system:
 \begin{align} \begin{cases} \displaystyle \frac{\partial U}{\partial t}=-d_m U+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{1}{\omega +\varepsilon }U(t{-}\tau,x-y)dy, \\[8pt] \displaystyle \frac{\partial V}{\partial t}=D\int _{\mathbb{R}}J(y)[V(t,x-y)-V(x,t)]dy -(1+\varepsilon )V \\[8pt] \displaystyle \, \, \, \, \, \, \, \ +d\int _{\mathbb{R}}k(y)\frac{1}{\omega +\varepsilon }U(t,x-y)dy, \end{cases} \end{align}
\begin{align} \begin{cases} \displaystyle \frac{\partial U}{\partial t}=-d_m U+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{1}{\omega +\varepsilon }U(t{-}\tau,x-y)dy, \\[8pt] \displaystyle \frac{\partial V}{\partial t}=D\int _{\mathbb{R}}J(y)[V(t,x-y)-V(x,t)]dy -(1+\varepsilon )V \\[8pt] \displaystyle \, \, \, \, \, \, \, \ +d\int _{\mathbb{R}}k(y)\frac{1}{\omega +\varepsilon }U(t,x-y)dy, \end{cases} \end{align}
where
![]() $t\gt 0$
,
$t\gt 0$
,
![]() $x\in \mathbb{R}$
. By a similar argument as that in the proof of Proposition 3.6, we can obtain that
$x\in \mathbb{R}$
. By a similar argument as that in the proof of Proposition 3.6, we can obtain that
![]() $P^\varepsilon _t$
satisfies (C1)–(C7) in [Reference Liang and Zhao20]. Moreover, for any given
$P^\varepsilon _t$
satisfies (C1)–(C7) in [Reference Liang and Zhao20]. Moreover, for any given
![]() $\varepsilon \in (0,1)$
, there exists
$\varepsilon \in (0,1)$
, there exists
![]() $\delta =(\delta _1,\delta _2)$
such that the solution
$\delta =(\delta _1,\delta _2)$
such that the solution
![]() $(U,V)$
of (3.15) satisfying
$(U,V)$
of (3.15) satisfying
for any initial
![]() $\phi =(\phi _1,\phi _2)$
with
$\phi =(\phi _1,\phi _2)$
with
![]() $0\leq \phi _1\leq \delta _1$
,
$0\leq \phi _1\leq \delta _1$
,
![]() $0\leq \phi _2\leq \delta _2$
. Hence,
$0\leq \phi _2\leq \delta _2$
. Hence,
![]() $(U(t,x;\,\phi ),V(t,x;\,\phi ))$
satisfies
$(U(t,x;\,\phi ),V(t,x;\,\phi ))$
satisfies
 \begin{align*} \frac{\partial U}{\partial t} & =-d_{m}U+\alpha e^{-d_i\tau }\int _{\Omega }k(y)\frac{U(t{-}\tau, x-y)}{U(t{-}\tau, x-y)+\omega }(V(t{-}\tau, x-y)+1)dy\\ & \geq -d_m U+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{1}{\omega +\varepsilon }U(t{-}\tau,x-y)dy, \ \ \ t\in [0,1], \end{align*}
\begin{align*} \frac{\partial U}{\partial t} & =-d_{m}U+\alpha e^{-d_i\tau }\int _{\Omega }k(y)\frac{U(t{-}\tau, x-y)}{U(t{-}\tau, x-y)+\omega }(V(t{-}\tau, x-y)+1)dy\\ & \geq -d_m U+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{1}{\omega +\varepsilon }U(t{-}\tau,x-y)dy, \ \ \ t\in [0,1], \end{align*}
and
 \begin{align*} \frac{\partial V}{\partial t} & =D\int _{\mathbb{R}}J(y)[V(t, x-y)-V(t, x)]dy-V(1+V) \\ &\ \ \ +d\int _{\Omega }k(y)\frac{U(t, x-y)}{U(t, x-y)+\omega }(V(t, x-y)+1)dy \\ &\geq D\int _{\mathbb{R}}J(y)[V(t,x-y)-V(t,x)]dy -(1+\varepsilon )V \\ &\ \ \ +d\int _{\mathbb{R}}k(y)\frac{1}{\omega +\varepsilon }U(t,x-y)dy, \ \ \ t\in [0,1]. \end{align*}
\begin{align*} \frac{\partial V}{\partial t} & =D\int _{\mathbb{R}}J(y)[V(t, x-y)-V(t, x)]dy-V(1+V) \\ &\ \ \ +d\int _{\Omega }k(y)\frac{U(t, x-y)}{U(t, x-y)+\omega }(V(t, x-y)+1)dy \\ &\geq D\int _{\mathbb{R}}J(y)[V(t,x-y)-V(t,x)]dy -(1+\varepsilon )V \\ &\ \ \ +d\int _{\mathbb{R}}k(y)\frac{1}{\omega +\varepsilon }U(t,x-y)dy, \ \ \ t\in [0,1]. \end{align*}
By the comparison principle, we obtain that
![]() $P^\varepsilon _t[\phi ]\leq Q_t[\phi ]$
for
$P^\varepsilon _t[\phi ]\leq Q_t[\phi ]$
for
![]() $t\in [0,1]$
. In particular,
$t\in [0,1]$
. In particular,
![]() $P^\varepsilon _1[\phi ]\leq Q_1[\phi ]$
for
$P^\varepsilon _1[\phi ]\leq Q_1[\phi ]$
for
![]() $0\leq \phi _1\leq \delta _1$
and
$0\leq \phi _1\leq \delta _1$
and
![]() $0\leq \phi _2\leq \delta _2$
. It then follows from [Reference Liang and Zhao20, Theorem 3.10] that the spreading speed of
$0\leq \phi _2\leq \delta _2$
. It then follows from [Reference Liang and Zhao20, Theorem 3.10] that the spreading speed of
![]() $P^\varepsilon _t$
can be attained by the infimum of
$P^\varepsilon _t$
can be attained by the infimum of
![]() $\Psi ^\varepsilon (\mu )\,:\!=\frac{\Lambda ^\varepsilon (\mu )}{\mu }$
, where
$\Psi ^\varepsilon (\mu )\,:\!=\frac{\Lambda ^\varepsilon (\mu )}{\mu }$
, where
![]() $\Lambda ^\varepsilon (\mu )$
is the principle eigenvalue of
$\Lambda ^\varepsilon (\mu )$
is the principle eigenvalue of
 \begin{align*} \left (\Lambda +d_m-\frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega +\varepsilon }e^{-\Lambda \tau }\right )\left (\Lambda -D\tilde{J}(\mu )+D+1+\varepsilon \right )=0, \end{align*}
\begin{align*} \left (\Lambda +d_m-\frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega +\varepsilon }e^{-\Lambda \tau }\right )\left (\Lambda -D\tilde{J}(\mu )+D+1+\varepsilon \right )=0, \end{align*}
which is the characteristic equation for the equation of
![]() $\eta$
corresponding to (3.15). It is easy to verify that the statements in Lemma 3.5 also hold for
$\eta$
corresponding to (3.15). It is easy to verify that the statements in Lemma 3.5 also hold for
![]() $\Psi ^\varepsilon (\mu )$
. Then we obtain
$\Psi ^\varepsilon (\mu )$
. Then we obtain
Since
![]() $\varepsilon \gt 0$
can be chosen arbitrarily, one further has
$\varepsilon \gt 0$
can be chosen arbitrarily, one further has
where
![]() $\Lambda (\mu )$
is the principal eigenvalue of
$\Lambda (\mu )$
is the principal eigenvalue of
 \begin{align*} \left (\Lambda +d_m-\frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega }e^{-\Lambda \tau }\right )\left (\Lambda -D\tilde{J}(\mu )+D+1\right )=0. \end{align*}
\begin{align*} \left (\Lambda +d_m-\frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega }e^{-\Lambda \tau }\right )\left (\Lambda -D\tilde{J}(\mu )+D+1\right )=0. \end{align*}
The proof is complete.
Remark 3.8. For a fixed
![]() $\mu \gt 0$
, we can compute that
$\mu \gt 0$
, we can compute that
![]() $\frac{\partial \mathcal{L}(\Lambda,\mu )}{\partial \Lambda }=1+\tau \frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega }e^{-\Lambda \tau }\gt 0$
and
$\frac{\partial \mathcal{L}(\Lambda,\mu )}{\partial \Lambda }=1+\tau \frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega }e^{-\Lambda \tau }\gt 0$
and
![]() $\mathcal{L}(0,\mu )=d_m-\frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega }$
. Since
$\mathcal{L}(0,\mu )=d_m-\frac{\alpha e^{-d_i\tau }\tilde{k}(\mu )}{\omega }$
. Since
![]() $d_m-\frac{\alpha e^{-d_i\tau }}{\omega }\lt 0$
by (H2) and
$d_m-\frac{\alpha e^{-d_i\tau }}{\omega }\lt 0$
by (H2) and
![]() $\tilde{k}(\mu )\gt 1$
for
$\tilde{k}(\mu )\gt 1$
for
![]() $\mu \gt 0$
by (H1), we have that
$\mu \gt 0$
by (H1), we have that
![]() $\mathcal{L}(0,\mu )\lt 0$
. Hence, the existence and uniqueness of
$\mathcal{L}(0,\mu )\lt 0$
. Hence, the existence and uniqueness of
![]() $\Lambda _2(\mu )$
can be easily obtained.
$\Lambda _2(\mu )$
can be easily obtained.
4. Travelling wavefronts
In this section, we shall prove the existence of travelling wavefronts with speed
![]() $c\geq c^*$
, and nonexistence of travelling wavefronts with speed
$c\geq c^*$
, and nonexistence of travelling wavefronts with speed
![]() $c\lt c^*$
, where
$c\lt c^*$
, where
![]() $c^*$
is the spreading speed defined in Section 3. A travelling wavefront of (2.1) is a monotone solution with the special form
$c^*$
is the spreading speed defined in Section 3. A travelling wavefront of (2.1) is a monotone solution with the special form
where
![]() $\xi =x+ct$
,
$\xi =x+ct$
,
![]() $c\gt 0$
is the wave speed. Substituting (4.1) into (2.1) gives
$c\gt 0$
is the wave speed. Substituting (4.1) into (2.1) gives
 \begin{align*} \begin{cases} c\varphi^{\prime}_1=-d_m\varphi _1+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\varphi _1(\xi -y-c\tau )}{\varphi _1(\xi -y-c\tau )+\omega }(\varphi _2(\xi -y-c\tau )+1)dy, \\ c\varphi^{\prime}_2=D\int _{\mathbb{R}}J(y)[\varphi _2(\xi -y)-\varphi _2(\xi )]dy-\varphi _2(1+\varphi _2) \\ \, \, \, \, \, \, \, \quad +d\int _{\mathbb{R}}k(y)\frac{\varphi _1(\xi -y)}{\varphi _1(\xi -y)+\omega }(\varphi _2(\xi -y)+1)dy, \end{cases} \end{align*}
\begin{align*} \begin{cases} c\varphi^{\prime}_1=-d_m\varphi _1+\alpha e^{-d_i\tau }\int _{\mathbb{R}}k(y)\frac{\varphi _1(\xi -y-c\tau )}{\varphi _1(\xi -y-c\tau )+\omega }(\varphi _2(\xi -y-c\tau )+1)dy, \\ c\varphi^{\prime}_2=D\int _{\mathbb{R}}J(y)[\varphi _2(\xi -y)-\varphi _2(\xi )]dy-\varphi _2(1+\varphi _2) \\ \, \, \, \, \, \, \, \quad +d\int _{\mathbb{R}}k(y)\frac{\varphi _1(\xi -y)}{\varphi _1(\xi -y)+\omega }(\varphi _2(\xi -y)+1)dy, \end{cases} \end{align*}
where
![]() $'$
denotes
$'$
denotes
![]() $\frac{d}{d\xi }$
.
$\frac{d}{d\xi }$
.
In Section 3, we have verified that the map
![]() $Q_t$
satisfies (A1)–(A5). Then, the nonexistence of travelling wavefronts of (2.1) follows from [Reference Liang and Zhao20, Theorem 4.3].
$Q_t$
satisfies (A1)–(A5). Then, the nonexistence of travelling wavefronts of (2.1) follows from [Reference Liang and Zhao20, Theorem 4.3].
Theorem 4.1.
Assume that (H1) and hold. Then, for any
![]() $0\lt c\lt c^{\ast }$
, system (2.1) has no travelling wavefronts connecting
$0\lt c\lt c^{\ast }$
, system (2.1) has no travelling wavefronts connecting
![]() $\mathbf{0}$
and
$\mathbf{0}$
and
![]() $\mathbf{K}$
.
$\mathbf{K}$
.
Since the solution map of (2.3) is not compact, we need to use the theory of travelling wavefronts developed in [Reference Fang and Zhao8] for monotone semiflows with weak compactness to establish the existence of travelling wavefronts of (2.1). Let
![]() $(X, X^+)$
be a Banach lattice with the norm
$(X, X^+)$
be a Banach lattice with the norm
![]() $\|\cdot \|$
and the positive cone
$\|\cdot \|$
and the positive cone
![]() $X^+$
. We use
$X^+$
. We use
![]() $\mathcal{M}$
to denote the set of all bounded and nondecreasing functions from
$\mathcal{M}$
to denote the set of all bounded and nondecreasing functions from
![]() $\mathbb{R}$
to
$\mathbb{R}$
to
![]() $X$
and equip
$X$
and equip
![]() $\mathcal{M}$
with the compact open topology. We use the Kuratowski measure of noncompactness in
$\mathcal{M}$
with the compact open topology. We use the Kuratowski measure of noncompactness in
![]() $X$
(see e.g. [Reference Carr and Chmaj5]), which is defined by
$X$
(see e.g. [Reference Carr and Chmaj5]), which is defined by
for any bounded set
![]() $B$
. It is easy to see that
$B$
. It is easy to see that
![]() $B$
is precompact (i.e. the closure of B is compact) if and only if
$B$
is precompact (i.e. the closure of B is compact) if and only if
![]() $\alpha (B) = 0$
. Let
$\alpha (B) = 0$
. Let
![]() $\beta \in Int X^+\not =\emptyset$
. We define
$\beta \in Int X^+\not =\emptyset$
. We define
![]() $X_\beta \,:\!=\{u \in X\,{:}\,0\le u\le \beta \}$
and
$X_\beta \,:\!=\{u \in X\,{:}\,0\le u\le \beta \}$
and
![]() $\mathcal{M}_\beta \,:\!= \{u\in \mathcal{M}\,{:}\,0 \le u\le \beta \}$
.
$\mathcal{M}_\beta \,:\!= \{u\in \mathcal{M}\,{:}\,0 \le u\le \beta \}$
.
By employing arguments similar to those in Lemma 2.1, we can easily prove the following well-posedness result.
Lemma 4.2.
For any initial value
![]() $\phi \,:\!= (\phi _1,\phi _2)\in \mathcal{M}_{\mathbf{K}}$
, system (2.3) has a unique non-negative solution
$\phi \,:\!= (\phi _1,\phi _2)\in \mathcal{M}_{\mathbf{K}}$
, system (2.3) has a unique non-negative solution
![]() $(U(t,x;\,\phi ),V(t,x;\,\phi ))$
which exists globally in time
$(U(t,x;\,\phi ),V(t,x;\,\phi ))$
which exists globally in time
![]() $t\ge {-}\tau$
, satisfying
$t\ge {-}\tau$
, satisfying
Definition 4.3.
A family of mappings
![]() $\{Q_t\}_{t\ge 0}$
is said to be a semiflow on
$\{Q_t\}_{t\ge 0}$
is said to be a semiflow on
![]() $\mathcal{M}_\beta$
, if the following three properties hold: (i)
$\mathcal{M}_\beta$
, if the following three properties hold: (i)
![]() $Q_0=I$
, where I is the identity mapping; (ii)
$Q_0=I$
, where I is the identity mapping; (ii)
![]() $Q_t\circ Q_s=Q_{t+s}$
for all
$Q_t\circ Q_s=Q_{t+s}$
for all
![]() $t, s\gt 0$
; (iii)
$t, s\gt 0$
; (iii)
![]() $t_n\rightarrow t$
and
$t_n\rightarrow t$
and
![]() $\phi _n\rightarrow \phi$
in
$\phi _n\rightarrow \phi$
in
![]() $\mathcal{M}_\beta$
, then both
$\mathcal{M}_\beta$
, then both
![]() $Q_{t_n}[\phi ](x)\rightarrow Q_t[\phi ](x)$
and
$Q_{t_n}[\phi ](x)\rightarrow Q_t[\phi ](x)$
and
![]() $Q_{t}[\phi _n](x)\rightarrow Q_t[\phi ](x)$
in
$Q_{t}[\phi _n](x)\rightarrow Q_t[\phi ](x)$
in
![]() $\mathcal{M}_\beta$
almost everywhere.
$\mathcal{M}_\beta$
almost everywhere.
Choose
![]() $X=\mathbb{R}^2$
and let
$X=\mathbb{R}^2$
and let
![]() $Q_t$
be the solution mapping of system (2.3), i.e.
$Q_t$
be the solution mapping of system (2.3), i.e.
where
where
![]() $\phi =(\phi _1, \phi _2)\in \mathcal{M}_{\mathbf{K}}$
and
$\phi =(\phi _1, \phi _2)\in \mathcal{M}_{\mathbf{K}}$
and
![]() $(U(t,x;\,\phi ), V(t,x;\,\phi ))$
is the mild solution of system (2.3).
$(U(t,x;\,\phi ), V(t,x;\,\phi ))$
is the mild solution of system (2.3).
Clearly, the solution mapping
![]() $\{Q_t\}_{t\ge 0}$
is a semiflow on
$\{Q_t\}_{t\ge 0}$
is a semiflow on
![]() $\mathcal{M}_{\mathbf{K}}$
. We need to verify that the solution semiflow
$\mathcal{M}_{\mathbf{K}}$
. We need to verify that the solution semiflow
![]() $Q_t$
satisfies the assumptions in [Reference Fang and Zhao8] for each
$Q_t$
satisfies the assumptions in [Reference Fang and Zhao8] for each
![]() $t \gt 0$
, which are listed as follows.
$t \gt 0$
, which are listed as follows.
-
(B1)
 $Q[\mathcal{R}[u]]=\mathcal{R}[Q[u]]$
,
$Q[\mathcal{R}[u]]=\mathcal{R}[Q[u]]$
,
 $T_{y}[Q[u]]=Q[T_{y}[u]]$
,
$T_{y}[Q[u]]=Q[T_{y}[u]]$
,
 $\forall y\in \mathbb{R}$
.
$\forall y\in \mathbb{R}$
. -
(B2)
 $Q\,{:}\,\mathcal{M}_{\mathbf{K}}\rightarrow \mathcal{M}_{\mathbf{K}}$
is continuous with respect to the compact open topology.
$Q\,{:}\,\mathcal{M}_{\mathbf{K}}\rightarrow \mathcal{M}_{\mathbf{K}}$
is continuous with respect to the compact open topology. -
(B3) (Point-
 $\alpha$
-contraction) There exists
$\alpha$
-contraction) There exists
 $k\in [0, 1)$
such that for any
$k\in [0, 1)$
such that for any
 $\mathcal{U}\subseteq \mathcal{M}_\beta$
,
$\mathcal{U}\subseteq \mathcal{M}_\beta$
,
 $\alpha (Q[\mathcal{U}](0))\le k\alpha (\mathcal{U}(0))$
.
$\alpha (Q[\mathcal{U}](0))\le k\alpha (\mathcal{U}(0))$
. -
(B4)
 $Q: \mathcal{M}_{\mathbf{K}}\rightarrow \mathcal{M}_{\mathbf{K}}$
is monotone in the sense that
$Q: \mathcal{M}_{\mathbf{K}}\rightarrow \mathcal{M}_{\mathbf{K}}$
is monotone in the sense that
 $Q[u]\geq Q(v)$
whenever
$Q[u]\geq Q(v)$
whenever
 $u\geq v$
in
$u\geq v$
in
 $\mathcal{M}_{\mathbf{K}}$
.
$\mathcal{M}_{\mathbf{K}}$
. -
(B5)
 $Q:\bar{\mathcal{C}}_{\mathbf{K}}\rightarrow \bar{\mathcal{C}}_{\mathbf{K}}$
admits exactly two fixed points
$Q:\bar{\mathcal{C}}_{\mathbf{K}}\rightarrow \bar{\mathcal{C}}_{\mathbf{K}}$
admits exactly two fixed points
 $\mathbf{0}$
and
$\mathbf{0}$
and
 $\mathbf{K}$
, and for any positive number
$\mathbf{K}$
, and for any positive number
 $\epsilon$
, there is a
$\epsilon$
, there is a
 $\zeta \in \bar{\mathcal{C}}_{\mathbf{K}}$
with
$\zeta \in \bar{\mathcal{C}}_{\mathbf{K}}$
with
 $\|\zeta \|\lt \epsilon$
such that
$\|\zeta \|\lt \epsilon$
such that
 $Q[\zeta ]\gg \zeta$
, where
$Q[\zeta ]\gg \zeta$
, where
 $\|\cdot \|$
is the maximum norm in
$\|\cdot \|$
is the maximum norm in
 $\bar{\mathcal{C}}$
.
$\bar{\mathcal{C}}$
.
Now we are in a position to prove the main result of this subsection.
Theorem 4.4.
Assume that (H1) and (H2) hold, let
![]() $c^*$
be the asymptotic spreading speed of
$c^*$
be the asymptotic spreading speed of
![]() $Q_t$
defined as in Theorem 3.4. Then, for any
$Q_t$
defined as in Theorem 3.4. Then, for any
![]() $c\geq c^{\ast }$
, system (2.1) admits a travelling wavefront
$c\geq c^{\ast }$
, system (2.1) admits a travelling wavefront
![]() $(\varphi _1(x+ct),\varphi _2(x+ct))$
connecting
$(\varphi _1(x+ct),\varphi _2(x+ct))$
connecting
![]() $\mathbf{0}$
and
$\mathbf{0}$
and
![]() $\mathbf{K}$
. Furthermore,
$\mathbf{K}$
. Furthermore,
![]() $(\varphi _1(x+ct),\varphi _2(x+ct))$
is also a classical solution to (2.1).
$(\varphi _1(x+ct),\varphi _2(x+ct))$
is also a classical solution to (2.1).
Proof. It is easy to see that each time-
![]() $t$
map
$t$
map
![]() $Q_t$
with
$Q_t$
with
![]() $t \gt 0$
satisfies (B1), (B2), (B4) and (B5) with
$t \gt 0$
satisfies (B1), (B2), (B4) and (B5) with
![]() $Q = Q_t$
. Thus, it remains to show that
$Q = Q_t$
. Thus, it remains to show that
![]() $Q_t$
satisfies the weak compactness assumption (B3). We write
$Q_t$
satisfies the weak compactness assumption (B3). We write
![]() $Q_t=L_t+S_t$
, where
$Q_t=L_t+S_t$
, where
 \begin{align*} L_t[\phi ](\theta,x)= \begin{cases} \phi (t+\theta,x)-\phi (0,x),\quad &t+\theta \lt 0,\\ 0,\quad &t+\theta \ge 0, \end{cases} \end{align*}
\begin{align*} L_t[\phi ](\theta,x)= \begin{cases} \phi (t+\theta,x)-\phi (0,x),\quad &t+\theta \lt 0,\\ 0,\quad &t+\theta \ge 0, \end{cases} \end{align*}
and
 \begin{align*} S_t[\phi ](\theta,x)= \begin{cases} \displaystyle\phi (0,x),\quad &t+\theta \lt 0,\\[6pt] \displaystyle Q_t[\phi ](\theta,x),\quad &t+\theta \ge 0. \end{cases} \end{align*}
\begin{align*} S_t[\phi ](\theta,x)= \begin{cases} \displaystyle\phi (0,x),\quad &t+\theta \lt 0,\\[6pt] \displaystyle Q_t[\phi ](\theta,x),\quad &t+\theta \ge 0. \end{cases} \end{align*}
For any bounded set
![]() $\mathcal{U}$
in
$\mathcal{U}$
in
![]() $\mathcal{M}_{\mathbf{K}}$
, the set
$\mathcal{M}_{\mathbf{K}}$
, the set
![]() $S_t[\mathcal{U}](\cdot, 0)$
is compact due to the uniform boundedness of the derivatives
$S_t[\mathcal{U}](\cdot, 0)$
is compact due to the uniform boundedness of the derivatives
![]() $(\partial _t U(t, 0; \,\phi ), \partial _t V(t, 0;\, \phi ))$
for
$(\partial _t U(t, 0; \,\phi ), \partial _t V(t, 0;\, \phi ))$
for
![]() $t \gt 0$
and
$t \gt 0$
and
![]() $\phi \in \mathcal{U}$
. On the other hand, by the
$\phi \in \mathcal{U}$
. On the other hand, by the
![]() $\alpha$
-contraction property of the solution map of delay differential equations (see e.g. [Reference Liang and Zhao21]), there exists some constant
$\alpha$
-contraction property of the solution map of delay differential equations (see e.g. [Reference Liang and Zhao21]), there exists some constant
![]() $\gamma \gt 0$
such that
$\gamma \gt 0$
such that
![]() $\alpha (L_t[\mathcal{U}](0))\le e^{-\gamma t}\alpha (\mathcal{U}(0))$
. Then we obtain that
$\alpha (L_t[\mathcal{U}](0))\le e^{-\gamma t}\alpha (\mathcal{U}(0))$
. Then we obtain that
for some positive
![]() $\gamma \gt 0$
, which implies that
$\gamma \gt 0$
, which implies that
![]() $Q_t$
satisfies
$Q_t$
satisfies
![]() $(B3)$
with
$(B3)$
with
![]() $k=e^{-\gamma t}$
. By [Reference Fang and Zhao8, Theorem 3.8], it follows that
$k=e^{-\gamma t}$
. By [Reference Fang and Zhao8, Theorem 3.8], it follows that
![]() $Q_t$
admits a left-continuous travelling wavefront connecting
$Q_t$
admits a left-continuous travelling wavefront connecting
![]() $\mathbf{0}$
and
$\mathbf{0}$
and
![]() $\mathbf{K}$
.
$\mathbf{K}$
.
Finally, we show that the obtained travelling wavefront
![]() $(\varphi _1(x+ct),\varphi _2(x+ct))$
for any
$(\varphi _1(x+ct),\varphi _2(x+ct))$
for any
![]() $c\geq c^*$
is also a classical solution of (2.1). Note that
$c\geq c^*$
is also a classical solution of (2.1). Note that
By the expression of
![]() $P(t)$
, it is easy to calculate that
$P(t)$
, it is easy to calculate that
which indicates that the right side of (4.2) is differential with respect to
![]() $t$
. Hence,
$t$
. Hence,
![]() $\varphi _2$
is differentiable. On the other hand,
$\varphi _2$
is differentiable. On the other hand,
which implies
![]() $\varphi _1^{\prime}$
exists for any
$\varphi _1^{\prime}$
exists for any
![]() $x\in \mathbb{R}$
. Hence,
$x\in \mathbb{R}$
. Hence,
![]() $(\varphi _1(x+ct), \varphi _2(x+ct))$
is also a classical solution to (2.1). The proof is complete.
$(\varphi _1(x+ct), \varphi _2(x+ct))$
is also a classical solution to (2.1). The proof is complete.
5. Conclusions
In this paper, we have studied the propagation dynamics of a mutualistic model of mistletoes and birds with nonlocal dispersal. We proved the well-posedness and the comparison principle for the initial value problem. We have also established the existence of the spreading speed and provided the upper and lower bound estimates of the spreading speed. In addition, the travelling wavefronts are considered again. Our result shows that the spreading speed coincides with the minimal wave speed of travelling wavefronts for this model. Our main methods are based on the comparison argument and the theory of asymptotic speeds of spread for the monotone semiflow developed in [Reference Fang and Zhao8, Reference Liang and Zhao20].
Financial support
The second author is supported by NSF of Gansu Province (21JR7RA121), NSF of China (12261081) and Department of Education of Gansu Province: Youth Doctoral Fund Project (2021QB-018). The first author is supported by 2022 Gansu Province Excellent Graduate Student "Innovation Star" Proiect (2022CXZX-239).
Competing interest
We declare that we have no Competing interest.