Consider a two-type Moran population of size N with selection and mutation, where the selective advantage of the fit individuals is amplified at extreme environmental conditions. Assume selection and mutation are weak with respect to N, and extreme environmental conditions rarely occur. We show that, as 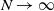$N\to\infty$, the type frequency process with time sped up by N converges to the solution to a Wright–Fisher-type SDE with a jump term modeling the effect of the environment. We use an extension of the ancestral selection graph (ASG) to describe the genealogical picture of the model. Next, we show that the type frequency process and the line-counting process of a pruned version of the ASG satisfy a moment duality. This relation yields a characterization of the asymptotic type distribution. We characterize the ancestral type distribution using an alternative pruning of the ASG. Most of our results are stated in annealed and quenched form.

We prove a result concerning the joint distribution of alleles at linked loci on a chromosome drawn from the population at stationarity. For a neutral locus, the allele is a draw from the stationary distribution of the mutation process. Furthermore, this allele is independent of the alleles at different loci on any chromosomes in the population.

We consider a nonneutral population genetics model with parent-independent mutations and two selective classes. We calculate the stationary distribution of the type of the common ancestor of a sample of genes from this model. The expected fitness of any ancestor (including the most recent common ancestor of any sample) is shown to be greater than the expected fitness of a randomly chosen gene from the population. The process of mutations to the common ancestor is also analysed. Our results are related to, but more general than, results obtained from diffusion theory.