Published online by Cambridge University Press: 09 March 2023
Consider a two-type Moran population of size N with selection and mutation, where the selective advantage of the fit individuals is amplified at extreme environmental conditions. Assume selection and mutation are weak with respect to N, and extreme environmental conditions rarely occur. We show that, as 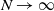 $N\to\infty$, the type frequency process with time sped up by N converges to the solution to a Wright–Fisher-type SDE with a jump term modeling the effect of the environment. We use an extension of the ancestral selection graph (ASG) to describe the genealogical picture of the model. Next, we show that the type frequency process and the line-counting process of a pruned version of the ASG satisfy a moment duality. This relation yields a characterization of the asymptotic type distribution. We characterize the ancestral type distribution using an alternative pruning of the ASG. Most of our results are stated in annealed and quenched form.
$N\to\infty$, the type frequency process with time sped up by N converges to the solution to a Wright–Fisher-type SDE with a jump term modeling the effect of the environment. We use an extension of the ancestral selection graph (ASG) to describe the genealogical picture of the model. Next, we show that the type frequency process and the line-counting process of a pruned version of the ASG satisfy a moment duality. This relation yields a characterization of the asymptotic type distribution. We characterize the ancestral type distribution using an alternative pruning of the ASG. Most of our results are stated in annealed and quenched form.