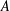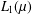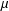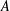In this doctoral thesis, we show how the bounded functional interpretation of F. Ferreira and P. Oliva can be used and contribute to the Proof Mining program, a program which aims to extract computational information from mathematical theorems using proof-theoretic techniques. We present a method for the elimination of sequential weak compactness arguments from the quantitative analysis of certain mathematical results. This method works as a “macro” and allowed us to obtain quantitative versions of important results of F. E. Browder, R. Wittmann, and H. H. Bauschke in fixed point theory in Hilbert spaces. Although the theorems of Browder and Wittmann were previously analyzed by U. Kohlenbach using the monotone functional interpretation, it was not clear why such analyses did not require the use of functionals defined by bar recursion. This phenomenon is now fully understood by a theoretical justification for the elimination of sequential weak compactness in the context of the bounded functional interpretation. Bauschke’s theorem is an important generalization of Wittmann’s theorem and its original proof is also analyzed here. The analyses of these results also require a quantitative version of a projection argument which turned out to be simpler when guided by the bounded functional interpretation than when using the monotone functional interpretation. In the context of the theory of monotone operators, results due to Boikanyo/Moroşanu and Xu for the strong convergence of variants of the proximal point algorithm are analyzed and bounds on the metastablility property of these iterations are obtained. These results are the first applications of the bounded functional interpretation to the proof mining of concrete mathematical results.

Abstract prepared by Pedro Pinto.

E-mail: [email protected]

URL: http://hdl.handle.net/10451/42661

We show that for a bounded subset $A$ of the $L_{1}(\unicode[STIX]{x1D707})$ space with finite measure $\unicode[STIX]{x1D707}$, the measure of weak noncompactness of $A$ based on the convex separation of sequences coincides with the measure of deviation from the Banach–Saks property expressed by the arithmetic separation of sequences. A similar result holds for a related quantity with the alternating signs Banach–Saks property. The results provide a geometric and quantitative extension of Szlenk’s theorem saying that every weakly convergent sequence in the Lebesgue space $L_{1}$ has a subsequence whose arithmetic means are norm convergent.

Let (E, ℱ) be a weakly compactly generated Frechet space and let ℱ0 be another weaker Hausdorff locally convex topology on E. Let X be an ℱ-bounded compact subset of (E, ℱ0). The ℱ0-closed convex hull of X in E is then ℱ0-compact. We also give a new proof, without using Riemann–Lebesgue-integrable (Birkoff-integrable) functions, with the result that if (E, ∥ · ∥) is any Banach space and ℱ0 is fragmented by ∥ · ∥, then the same result holds. Furthermore, the closure of the convex hull of X in ℱ0-topology and in the original topology of E is the same.

We study countable splitting of Markushevich bases in weakly Lindelöf Banach spaces in connection with the geometry of these spaces.