Article contents
A QUANTITATIVE EXTENSION OF SZLENK’S THEOREM
Published online by Cambridge University Press: 20 February 2019
Abstract
We show that for a bounded subset 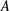 $A$ of the
$A$ of the 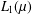 $L_{1}(\unicode[STIX]{x1D707})$ space with finite measure
$L_{1}(\unicode[STIX]{x1D707})$ space with finite measure 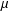 $\unicode[STIX]{x1D707}$, the measure of weak noncompactness of
$\unicode[STIX]{x1D707}$, the measure of weak noncompactness of 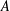 $A$ based on the convex separation of sequences coincides with the measure of deviation from the Banach–Saks property expressed by the arithmetic separation of sequences. A similar result holds for a related quantity with the alternating signs Banach–Saks property. The results provide a geometric and quantitative extension of Szlenk’s theorem saying that every weakly convergent sequence in the Lebesgue space
$A$ based on the convex separation of sequences coincides with the measure of deviation from the Banach–Saks property expressed by the arithmetic separation of sequences. A similar result holds for a related quantity with the alternating signs Banach–Saks property. The results provide a geometric and quantitative extension of Szlenk’s theorem saying that every weakly convergent sequence in the Lebesgue space 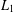 $L_{1}$ has a subsequence whose arithmetic means are norm convergent.
$L_{1}$ has a subsequence whose arithmetic means are norm convergent.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 338 - 343
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by


