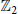8 results
3 - Objectivity of Transport Barriers
-
- Book:
- Transport Barriers and Coherent Structures in Flow Data
- Published online:
- 20 February 2023
- Print publication:
- 16 March 2023, pp 60-97
-
- Chapter
- Export citation
THE BOCHNER–SCHOENBERG-EBERLEIN PROPERTY OF EXTENSIONS OF BANACH ALGEBRAS AND BANACH MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 09 July 2021, pp. 134-145
- Print publication:
- February 2022
-
- Article
- Export citation
Vector field path following of a full-wing solar-powered Unmanned Aerial Vehicle (UAV) landing based on Dubins path: a lesson from multiple landing failures
-
- Journal:
- The Aeronautical Journal / Volume 125 / Issue 1290 / August 2021
- Published online by Cambridge University Press:
- 13 April 2021, pp. 1283-1312
-
- Article
- Export citation
7 - FEA for Multi-Dimensional Vector Field Problems
-
- Book:
- Introduction to the Finite Element Method and Implementation with MATLAB®
- Published online:
- 09 December 2020
- Print publication:
- 30 July 2020, pp 319-404
-
- Chapter
- Export citation
Global Phase Portraits for the Abel Quadratic Polynomial Differential Equations of the Second Kind With Z2-symmetries
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 149-165
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
Vector Fields Tangent to Foliations
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 51 / Issue 3 / October 2008
- Published online by Cambridge University Press:
- 12 December 2008, pp. 765-778
-
- Article
-
- You have access
- Export citation
Real and complex indices of vector fields on complete intersection curves with isolated singularity
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 2 / March 2005
- Published online by Cambridge University Press:
- 10 February 2005, pp. 525-540
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation