Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-10T12:43:32.643Z Has data issue: false hasContentIssue false
  • English
  • Français

THE BOCHNER–SCHOENBERG-EBERLEIN PROPERTY OF EXTENSIONS OF BANACH ALGEBRAS AND BANACH MODULES

Part of: Commutative Banach algebras and commutative topological algebras

Published online by Cambridge University Press:  09 July 2021

NASRIN ALIZADEH Open the ORCID record for NASRIN ALIZADEH [Opens in a new window] ,
ALI EBADIAN Open the ORCID record for ALI EBADIAN [Opens in a new window] ,
SAEID OSTADBASHI Open the ORCID record for SAEID OSTADBASHI [Opens in a new window]  and
ALI JABBARI Open the ORCID record for ALI JABBARI [Opens in a new window]
NASRIN ALIZADEH
Affiliation:
Department of Mathematics, Faculty of Science, Urmia University, Urmia, Iran e-mail: [email protected]
ALI EBADIAN*
Affiliation:
Department of Mathematics, Faculty of Science, Urmia University, Urmia, Iran
SAEID OSTADBASHI
Affiliation:
Department of Mathematics, Faculty of Science, Urmia University, Urmia, Iran e-mail: [email protected]
ALI JABBARI
Affiliation:
Department of Mathematics, Faculty of Science, Urmia University, Urmia, Iran e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

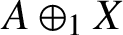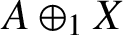Let A be a Banach algebra and let X be a Banach A-bimodule. We consider the Banach algebra ${A\oplus _1 X}$ , where A is a commutative Banach algebra. We investigate the Bochner–Schoenberg–Eberlein (BSE) property and the BSE module property on $A\oplus _1 X$ . We show that the module extension Banach algebra $A\oplus _1 X$ is a BSE Banach algebra if and only if A is a BSE Banach algebra and 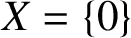$X=\{0\}$ . Furthermore, we consider 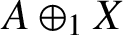$A\oplus _1 X$ as a Banach $A\oplus _1 X$ -module and characterise the BSE module property on $A\oplus _1 X$ . 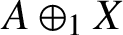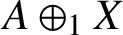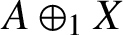We show that $A\oplus _1 X$ is a BSE Banach 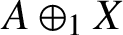$A\oplus _1 X$ -module if and only if A and X are BSE Banach A-modules.

Keywords

BSE Banach algebraBSE Banach modulecharacterlocally compact groupmodule extension Banach algebramultipliervector field

MSC classification

Primary: 46J05: General theory of commutative topological algebras
Secondary: 46J20: Ideals, maximal ideals, boundaries
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 134 - 145
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abtahi, F., Kamali, Z. and Toutounchi, M., ‘The Bochner–Schoenberg–Eberlein property for vector-valued Lipschitz algebras’, J. Math. Anal. Appl. 479(1) (2019), 1172–1181.CrossRefGoogle Scholar
Bade, W. G., Dales, H. G. and Lykova, Z. A., Algebraic and Strong Splittings of Extensions of Banach Algebras, Memoirs of the American Mathematical Society, 137(656) (American Mathematical Society, Providence, RI, 1999).CrossRefGoogle Scholar
Daws, M., ‘Multipliers, self-induced and dual Banach algebras’, Diss. Math. 470 (2010), 1–62.Google Scholar
Essmaili, M. and Filali, M., ‘ $\phi$ -amenability and character amenability of some classes of Banach algebras’, Houston J. Math. 39(2) (2013), 515–529.Google Scholar
Fozouni, M. and Nemati, M., ‘BSE-property for some certain Segal and Banach algebras’, Mediterr. J. Math. 16(2) (2019), Article ID 38.CrossRefGoogle Scholar
Jabbari, A. and Ebadian, A., ‘The second cohomology group of module extensions Banach algebras’, Rocky Mountain J. Math., to appear.Google Scholar
Kamali, Z. and Lashkarizadeh Bami, M., ‘The multiplier algebra and BSE property of the direct sum of Banach algebras’, Bull. Aust. Math. Soc. 88 (2013), 250–258.CrossRefGoogle Scholar
Kamali, Z. and Lashkarizadeh, M., ‘The Bochner–Schoenberg–Eberlein property for ${L}^1\left({\mathbb{R}}^{+}\right)$ ’, J. Fourier Anal. Appl. 20(2) (2014), 225–233.CrossRefGoogle Scholar
Kamali, Z. and Lashkarizadeh, M., ‘The Bochner–Schoenberg–Eberlein property for totally ordered semigroup algebras’, J. Fourier Anal. Appl. 22(6) (2016), 1225–1234.CrossRefGoogle Scholar
Kaniuth, E., ‘The Bochner–Schoenberg–Eberlein property and spectral synthesis for certain Banach algebra products’, Canad. J. Math. 67 (2015), 827–847.CrossRefGoogle Scholar
Kaniuth, E. and Ülger, A., ‘The Bochner–Schoenberg–Eberlein property for commutative Banach algebras, especially Fourier and Fourier–Stieltjes algebras’, Trans. Amer. Math. Soc. 362 (2010), 4331–4356.CrossRefGoogle Scholar
Larsen, R., An Introduction to the Theory of Multipliers (Springer, New York, 1971).CrossRefGoogle Scholar
Medghalchi, A. R. and Pourmahmood-Aghababa, H., ‘The first cohomology group of module extension Banach algebras’, Rocky Mountain J. Math. 41(5) (2011), 1639–1651.CrossRefGoogle Scholar
Rudin, W., Fourier Analysis on Groups (Wiley Interscience, New York, 1962).Google Scholar
Takahasi, S.-E., ‘BSE Banach modules and multipliers’, J. Funct. Anal. 125 (1994), 67–68.CrossRefGoogle Scholar
Takahasi, S.-E. and Hatori, O., ‘Commutative Banach algebras which satisfy a Bochner–Schoenberg–Eberlein-type theorem’, Proc. Amer. Math. Soc. 110 (1990), 148–158.Google Scholar
Zhang, Y., ‘Weak amenability of module extensions of Banach algebras’, Trans. Amer. Math. Soc. 354(10) (2002), 4131–4151.CrossRefGoogle Scholar