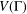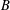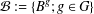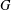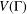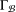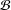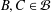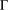2 results
FINITE SYMMETRIC GRAPHS WITH 2-ARC-TRANSITIVE QUOTIENTS: AFFINE CASE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 17 September 2015, pp. 13-18
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Algebras with Transitive Automorphism Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 2 / 01 June 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 224-226
- Print publication:
- 01 June 1986
-
- Article
-
- You have access
- Export citation