Published online by Cambridge University Press: 17 September 2015
Let 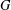 $G$ be a finite group and
$G$ be a finite group and 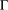 ${\rm\Gamma}$ a
${\rm\Gamma}$ a 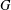 $G$-symmetric graph. Suppose that
$G$-symmetric graph. Suppose that 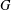 $G$ is imprimitive on
$G$ is imprimitive on 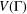 $V({\rm\Gamma})$ with
$V({\rm\Gamma})$ with 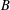 $B$ a block of imprimitivity and
$B$ a block of imprimitivity and 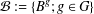 ${\mathcal{B}}:=\{B^{g};g\in G\}$ a system of imprimitivity of
${\mathcal{B}}:=\{B^{g};g\in G\}$ a system of imprimitivity of 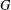 $G$ on
$G$ on 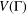 $V({\rm\Gamma})$. Define
$V({\rm\Gamma})$. Define 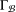 ${\rm\Gamma}_{{\mathcal{B}}}$ to be the graph with vertex set
${\rm\Gamma}_{{\mathcal{B}}}$ to be the graph with vertex set 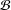 ${\mathcal{B}}$ such that two blocks
${\mathcal{B}}$ such that two blocks 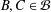 $B,C\in {\mathcal{B}}$ are adjacent if and only if there exists at least one edge of
$B,C\in {\mathcal{B}}$ are adjacent if and only if there exists at least one edge of 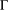 ${\rm\Gamma}$ joining a vertex in
${\rm\Gamma}$ joining a vertex in 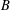 $B$ and a vertex in
$B$ and a vertex in 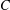 $C$. Xu and Zhou [‘Symmetric graphs with 2-arc-transitive quotients’, J. Aust. Math. Soc. 96 (2014), 275–288] obtained necessary conditions under which the graph
$C$. Xu and Zhou [‘Symmetric graphs with 2-arc-transitive quotients’, J. Aust. Math. Soc. 96 (2014), 275–288] obtained necessary conditions under which the graph 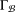 ${\rm\Gamma}_{{\mathcal{B}}}$ is 2-arc-transitive. In this paper, we completely settle one of the cases defined by certain parameters connected to
${\rm\Gamma}_{{\mathcal{B}}}$ is 2-arc-transitive. In this paper, we completely settle one of the cases defined by certain parameters connected to 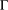 ${\rm\Gamma}$ and
${\rm\Gamma}$ and 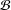 ${\mathcal{B}}$ and show that there is a unique graph corresponding to this case.
${\mathcal{B}}$ and show that there is a unique graph corresponding to this case.