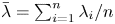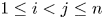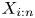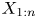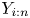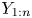3 results
Dependence comparisons of order statistics in the proportional hazards model
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 21 April 2022, pp. 730-736
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
OPTIMUM INSURANCE CONTRACTS WITH BACKGROUND RISK AND HIGHER-ORDER RISK ATTITUDES
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 48 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 25 April 2018, pp. 1025-1047
- Print publication:
- September 2018
-
- Article
- Export citation
Stability and structural properties of stochastic storage networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1169-1180
- Print publication:
- December 1996
-
- Article
- Export citation