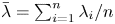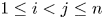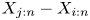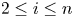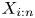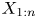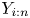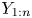1. Introduction
Several notions of monotone dependence have been introduced and studied in the literature. Researchers have also developed the corresponding dependence (partial) orderings which compare the degree of (monotone) dependence within the components of different random vectors of the same length. For details, see the pioneering paper of Lehmann [Reference Lehmann16] and Chapter 5 of Barlow and Proschan [Reference Barlow and Proschan2] for different notions of positive dependence, and that of Kimeldorf and Sampson [Reference Kimeldorf and Sampson12] for a unified treatment of families, orderings and measures of monotone dependence. For more detailed discussion of these concepts, see Chapter 2 of Joe [Reference Joe9] and Chapter 5 of Nelsen [Reference Nelsen17].
Let ![]() $\{X_1, \ldots, X_n\}$ be a set of continuous random variables. Many authors have investigated the nature of the dependence that may exist between two order statistics
$\{X_1, \ldots, X_n\}$ be a set of continuous random variables. Many authors have investigated the nature of the dependence that may exist between two order statistics ![]() $X_{i:n}$ and
$X_{i:n}$ and ![]() $X_{j:n}$ for
$X_{j:n}$ for ![]() $1 \le i \lt j \le n$ under different distributional scenarios. It seems natural to expect some degree of positive dependence between them. It is well known that the order statistics based on independent (but not necessarily identically distributed) random variables are associated (cf., [Reference Barlow and Proschan2, p. 32]). This yields many useful product inequalities for order statistics of independent random variables, and in particular,
$1 \le i \lt j \le n$ under different distributional scenarios. It seems natural to expect some degree of positive dependence between them. It is well known that the order statistics based on independent (but not necessarily identically distributed) random variables are associated (cf., [Reference Barlow and Proschan2, p. 32]). This yields many useful product inequalities for order statistics of independent random variables, and in particular, ![]() ${\rm Cov}(X_{i:n},X_{j:n}) \geq 0$ for all
${\rm Cov}(X_{i:n},X_{j:n}) \geq 0$ for all ![]() $i$ and
$i$ and ![]() $j$, which was initially proved by Bickel [Reference Bickel, LeCam and Neyman3] when the
$j$, which was initially proved by Bickel [Reference Bickel, LeCam and Neyman3] when the ![]() $X$'s are independent and identically distributed (i.i.d.).
$X$'s are independent and identically distributed (i.i.d.).
Boland et al. [Reference Boland, Hollander, Joag-Dev and Kochar4] studied the problem of dependence among order statistics in detail and discussed different types of dependence that hold between them. It is shown in that paper that in the case of i.i.d. observations, any pair of order statistics is ![]() $TP_2$ dependent (also called monotone likelihood ratio dependent) which is the strongest type of dependence in the hierarchy of various dependence criteria as described in [Reference Barlow and Proschan2]). But this is not the case in the non-i.i.d. case. However, as is shown in Boland et al. [Reference Boland, Hollander, Joag-Dev and Kochar4], in general, whereas
$TP_2$ dependent (also called monotone likelihood ratio dependent) which is the strongest type of dependence in the hierarchy of various dependence criteria as described in [Reference Barlow and Proschan2]). But this is not the case in the non-i.i.d. case. However, as is shown in Boland et al. [Reference Boland, Hollander, Joag-Dev and Kochar4], in general, whereas ![]() $X_{j:n}$ may not be stochastically increasing in
$X_{j:n}$ may not be stochastically increasing in ![]() $X_{i:n}$ for
$X_{i:n}$ for ![]() $i \lt j$,
$i \lt j$, ![]() $X_{j:n}$ is always right tail increasing (RTI) in
$X_{j:n}$ is always right tail increasing (RTI) in ![]() $X_{i:n}$. The reader is referred to Chapter 5 of Barlow and Proschan [Reference Barlow and Proschan2] for basic definitions and relations among various types of dependence.
$X_{i:n}$. The reader is referred to Chapter 5 of Barlow and Proschan [Reference Barlow and Proschan2] for basic definitions and relations among various types of dependence.
It is also of interest to compare the strength of dependence that may exist between two pairs of order statistics. When the parent distribution from which the random sample is drawn has an increasing hazard rate and a decreasing reverse hazard rate, Tukey [Reference Tukey22] showed that
for either ![]() $i=i'$ and
$i=i'$ and ![]() $j\le j'$; or
$j\le j'$; or ![]() $j=j'$ and
$j=j'$ and ![]() $i'\le i$. Kim and David [Reference Kim and David11] proved that if both the hazard and the reverse hazard rates of the
$i'\le i$. Kim and David [Reference Kim and David11] proved that if both the hazard and the reverse hazard rates of the ![]() $X_i$'s are increasing, then inequality (1.1) remains valid when
$X_i$'s are increasing, then inequality (1.1) remains valid when ![]() $i=i'$ and
$i=i'$ and ![]() $j\le j'$; However, the inequality (1.1) is reversed when
$j\le j'$; However, the inequality (1.1) is reversed when ![]() $j=j'$ and
$j=j'$ and ![]() $i'\le i$.
$i'\le i$.
Let ![]() $X_1, \ldots, X_n$ be mutually independent exponentials with distinct hazard rates
$X_1, \ldots, X_n$ be mutually independent exponentials with distinct hazard rates ![]() $\lambda _1, \ldots, \lambda _n$ and let
$\lambda _1, \ldots, \lambda _n$ and let ![]() $Y_1, \ldots, Y_n$ form a random sample from the exponential distribution with hazard rate
$Y_1, \ldots, Y_n$ form a random sample from the exponential distribution with hazard rate ![]() $\bar {\lambda } = ( \sum _{i=1}^{n} X_i)/n$. Sathe [Reference Sathe18] proved that for any
$\bar {\lambda } = ( \sum _{i=1}^{n} X_i)/n$. Sathe [Reference Sathe18] proved that for any ![]() $i \in \{2,\ldots,n\}$
$i \in \{2,\ldots,n\}$
Although this observation is interesting, it merely compares the relative degree of linear association within the two pairs. It is now widely recognized, however, that margin-free measures of association are more appropriate than Pearson's correlation, because they are based on the unique underlying copula which governs the dependence between the components of a continuous random pair.
In this paper, a long-standing open problem that for ![]() $1\le i \lt j \le n$, the generalized spacing
$1\le i \lt j \le n$, the generalized spacing ![]() $X_{j:n} - X_{i:n}$ is more dispersed than
$X_{j:n} - X_{i:n}$ is more dispersed than ![]() $Y_{j:n} - Y_{i:n}$ according to dispersive ordering, has been solved (cf. [Reference Xu and Balakrishnan23]). This result is used to solve a related open problem that for
$Y_{j:n} - Y_{i:n}$ according to dispersive ordering, has been solved (cf. [Reference Xu and Balakrishnan23]). This result is used to solve a related open problem that for ![]() $2\le i \le n$, the dependence of
$2\le i \le n$, the dependence of ![]() $X_{i:n}$ on
$X_{i:n}$ on ![]() $X_{1:n}$ is less than that of
$X_{1:n}$ is less than that of ![]() $Y_{i:n}$ on
$Y_{i:n}$ on ![]() $Y_{1:n}$, in the sense of the more stochastically increasing ordering. This dependence result is also extended to the proportional hazard rates (PHR) model. This extends the earlier work of Genest et al. [Reference Genest, Kochar and Xu8] who proved this result for
$Y_{1:n}$, in the sense of the more stochastically increasing ordering. This dependence result is also extended to the proportional hazard rates (PHR) model. This extends the earlier work of Genest et al. [Reference Genest, Kochar and Xu8] who proved this result for ![]() $i =n$. Section 2 is on some preliminaries where various definitions and notations are given. The main results of this paper are given in Section 3.
$i =n$. Section 2 is on some preliminaries where various definitions and notations are given. The main results of this paper are given in Section 3.
2. Preliminaries
For ![]() $i = 1, 2$, let
$i = 1, 2$, let ![]() $(X_i, Y_i)$ be a pair of continuous random variables with joint cumulative distribution function
$(X_i, Y_i)$ be a pair of continuous random variables with joint cumulative distribution function ![]() $H_i$ and margins
$H_i$ and margins ![]() $F_i$,
$F_i$, ![]() $G_i$. Let
$G_i$. Let
be the unique copula associated with ![]() $H_i$. In other words,
$H_i$. In other words, ![]() $C_i$ is the distribution of the pair
$C_i$ is the distribution of the pair ![]() $(U_i,V_i) \equiv (F_i(X_i),G_i(Y_i))$ whose margins are uniform on the interval
$(U_i,V_i) \equiv (F_i(X_i),G_i(Y_i))$ whose margins are uniform on the interval ![]() $(0,1)$. See, for example, Chapter 1 of Nelsen [Reference Nelsen17] for details.
$(0,1)$. See, for example, Chapter 1 of Nelsen [Reference Nelsen17] for details.
The most well-understood partial order to compare the strength of dependence within two random vectors is that of positive quadrant dependence (PQD) as defined below.
Definition 2.1. A copula ![]() $C_1$ is said to be less dependent than copula
$C_1$ is said to be less dependent than copula ![]() $C_2$ in the positive quadrant dependence (PQD) ordering, denoted
$C_2$ in the positive quadrant dependence (PQD) ordering, denoted ![]() $(X_1, Y_1) \prec _{\rm PQD} (X_2, Y_2)$, if and only if
$(X_1, Y_1) \prec _{\rm PQD} (X_2, Y_2)$, if and only if
This condition implies that ![]() $\kappa (S_1, T_1) \le \kappa (S_2, T_2)$ for all concordance measures meeting the axioms of Scarsini [Reference Scarsini19] like Kendall's
$\kappa (S_1, T_1) \le \kappa (S_2, T_2)$ for all concordance measures meeting the axioms of Scarsini [Reference Scarsini19] like Kendall's ![]() $\tau$ and Spearman's
$\tau$ and Spearman's ![]() $\rho$. See Tchen [Reference Tchen21] for details.
$\rho$. See Tchen [Reference Tchen21] for details.
Lehmann [Reference Lehmann16] in his seminal work introduced the notion of monotone regression dependence (MRD) which is also known as stochastic increasingness (SI) in the literature.
Definition 2.2. Let ![]() $(X,Y)$ be a bivariate random vector with joint distribution function
$(X,Y)$ be a bivariate random vector with joint distribution function ![]() $H$. The variable
$H$. The variable ![]() $Y$ is said to be stochastically increasing (SI) in
$Y$ is said to be stochastically increasing (SI) in ![]() $X$ if for all
$X$ if for all ![]() $(x_1,x_2) \in {I\!\!R}^{2}$,
$(x_1,x_2) \in {I\!\!R}^{2}$,
If we denote by ![]() $H_x$ the distribution function of the conditional distribution of
$H_x$ the distribution function of the conditional distribution of ![]() $Y$ given
$Y$ given ![]() $X=x$, then (2.1) can be rewritten as
$X=x$, then (2.1) can be rewritten as
Note that in case ![]() $X$ and
$X$ and ![]() $Y$ are independent,
$Y$ are independent, ![]() $H_{x_2}\circ H_{x_1}^{-1}(u) = u$, for
$H_{x_2}\circ H_{x_1}^{-1}(u) = u$, for ![]() $0 \le u \le 1$ and for all
$0 \le u \le 1$ and for all ![]() $(x_1, x_2)$. The SI property is not symmetric in
$(x_1, x_2)$. The SI property is not symmetric in ![]() $X$ and
$X$ and ![]() $Y$. It is a very strong notion of positive dependence and many of the other notions of positive dependence follow from it.
$Y$. It is a very strong notion of positive dependence and many of the other notions of positive dependence follow from it.
Denoting by ![]() $\xi _p = {F^{-1}}(p)$, the
$\xi _p = {F^{-1}}(p)$, the ![]() $p$th quantile of the marginal distribution of
$p$th quantile of the marginal distribution of ![]() $X$, we see that (2.2) will hold if and only if for all
$X$, we see that (2.2) will hold if and only if for all ![]() $0\le u \le 1$,
$0\le u \le 1$,
In his book, Joe [Reference Joe9] mentions a number of bivariate stochastic ordering relations. One such notion is that of greater monotone regression (or more SI) dependence, originally considered by Yanagimoto and Okamoto [Reference Yanagimoto and Okamoto24] and later extended and further investigated by Schriever [Reference Schriever20], Capéraà and Genest [Reference Capéraà and Genest5], and Avérous et al. [Reference Avérous, Genest and Kochar1], among others.
As discussed in the books by Joe [Reference Joe9] and Nelsen [Reference Nelsen17], a reasonable way to compare the relative degree of dependence between two random vectors is through their copulas. We will discuss here the concept of more SI, a partial order to compare the strength of dependence that may exist between two bivariate random vectors in the sense of monotone regression dependence (stochastic increasingness).
Suppose we have two pairs of continuous random variables ![]() $(X_1,Y_1)$ and
$(X_1,Y_1)$ and ![]() $(X_2,Y_2)$ with joint cumulative distribution functions
$(X_2,Y_2)$ with joint cumulative distribution functions ![]() $H_i$ and marginals
$H_i$ and marginals ![]() $F_i$ and
$F_i$ and ![]() $G_i$ for
$G_i$ for ![]() $i=1,2$.
$i=1,2$.
Definition 2.3. ![]() $Y_2$ is said to be more stochastically increasing in
$Y_2$ is said to be more stochastically increasing in ![]() $X_2$ than
$X_2$ than ![]() $Y_1$ is in
$Y_1$ is in ![]() $X_1$, denoted by
$X_1$, denoted by ![]() $(Y_1 \,| \, X_1) \prec _{\rm SI} (Y_2\, | \, X_2)$ or
$(Y_1 \,| \, X_1) \prec _{\rm SI} (Y_2\, | \, X_2)$ or ![]() $H_1 \prec _{\rm SI} H_2$, if
$H_1 \prec _{\rm SI} H_2$, if
for all ![]() $u \in (0,1)$, where for
$u \in (0,1)$, where for ![]() $i=1,2$,
$i=1,2$, ![]() $H_{i, s}$ denotes the conditional distribution of
$H_{i, s}$ denotes the conditional distribution of ![]() $Y_i$ given
$Y_i$ given ![]() $X_i = s$, and
$X_i = s$, and ![]() $\xi _{ip} = F_i^{-1} (p)$ stands for the
$\xi _{ip} = F_i^{-1} (p)$ stands for the ![]() $p$th quantile of the marginal distribution of
$p$th quantile of the marginal distribution of ![]() $X_i$.
$X_i$.
Obviously, (2.3) implies that ![]() $Y_2$ is stochastically increasing in
$Y_2$ is stochastically increasing in ![]() $X_2$ if
$X_2$ if ![]() $X_1$ and
$X_1$ and ![]() $Y_1$ are independent. It also implies that if
$Y_1$ are independent. It also implies that if ![]() $Y_1$ is stochastically increasing in
$Y_1$ is stochastically increasing in ![]() $X_1$, then so is
$X_1$, then so is ![]() $Y_2$ in
$Y_2$ in ![]() $X_2$; and conversely, if
$X_2$; and conversely, if ![]() $Y_2$ is stochastically decreasing in
$Y_2$ is stochastically decreasing in ![]() $X_2$, then so is
$X_2$, then so is ![]() $Y_1$ in
$Y_1$ in ![]() $X_1$. The above definition of more SI is copula based and
$X_1$. The above definition of more SI is copula based and
Avérous et al. [Reference Avérous, Genest and Kochar1] have shown in their paper that in the case of i.i.d. observations, the copula of any pair of order statistics is independent of the distribution of the parent observations as long as they are continuous. In a sense, their copula has a distribution-free property. But this is not the case if the observations are not i.i.d.
The natural question is to see if we can extend the result given in (1.2) to a copula-based positive dependence ordering. Genest et al. [Reference Genest, Kochar and Xu8] proved that under the given conditions,
It has been an open problem to see whether this result can be generalized from the the largest order statistic to other order statistics. We prove in this paper that for ![]() $2\le i \le n$,
$2\le i \le n$,
This implies in particular that
where ![]() $\kappa (S,T)$ represents any concordance measure between random variables
$\kappa (S,T)$ represents any concordance measure between random variables ![]() $S$ and
$S$ and ![]() $T$ in the sense of Scarsini [Reference Scarsini19], for example, Spearman's rho or Kendall's tau. A related work to this problem is Dolati et al. [Reference Dolati, Genest and Kochar7].
$T$ in the sense of Scarsini [Reference Scarsini19], for example, Spearman's rho or Kendall's tau. A related work to this problem is Dolati et al. [Reference Dolati, Genest and Kochar7].
3. Main results
The proof of our main result relies heavily on the notion of dispersive ordering between two random variables ![]() $X$ and
$X$ and ![]() $Y$, and properties thereof. For completeness, the definition of this concept is recalled below.
$Y$, and properties thereof. For completeness, the definition of this concept is recalled below.
Definition 3.1. A random variable ![]() $X$ with distribution function
$X$ with distribution function ![]() $F$ is said to be less dispersed than another variable
$F$ is said to be less dispersed than another variable ![]() $Y$ with distribution
$Y$ with distribution ![]() $G$, written as
$G$, written as ![]() $X \le _{{\rm disp}} Y$ or
$X \le _{{\rm disp}} Y$ or ![]() $F \le _{{\rm disp}} G$, if and only if
$F \le _{{\rm disp}} G$, if and only if
for all ![]() $0 \lt u \le v \lt 1$.
$0 \lt u \le v \lt 1$.
The dispersive order is closely related to the star-ordering which is a partial order to compare the relative aging or skewness and is defined as below.
Definition 3.2. A random variable ![]() $X$ with distribution function
$X$ with distribution function ![]() $F$ is said to be star ordered with respect to another random variable
$F$ is said to be star ordered with respect to another random variable ![]() $Y$ with distribution
$Y$ with distribution ![]() $G$, written as
$G$, written as ![]() $X \le _{*} Y$ or
$X \le _{*} Y$ or ![]() $F \le _{*} G$, if and only if
$F \le _{*} G$, if and only if
For nonnegative random variables, the star order is related to the dispersive order by
The proof of the next lemma, which is a refined version of a result by Deshpande and Kochar [Reference Deshpandé and Kochar6], on relation between the star order and the dispersive order, can be found in Kochar and Xu [Reference Kochar and Xu15].
Lemma 3.1. Let ![]() $X$ and
$X$ and ![]() $Y$ be two random variables. If
$Y$ be two random variables. If ![]() $X \le _{*} Y$ and
$X \le _{*} Y$ and ![]() $X \le _{{\rm st}} Y$, then
$X \le _{{\rm st}} Y$, then ![]() $X\le _{{\rm disp}} Y$.
$X\le _{{\rm disp}} Y$.
The following result of Khaledi and Kochar [Reference Khaledi and Kochar10] will be used to prove our main theorem.
Lemma 3.2. ([Reference Khaledi and Kochar10])
Let ![]() $X_i$ and
$X_i$ and ![]() $Y_i$ be independent random variables with distribution functions
$Y_i$ be independent random variables with distribution functions ![]() $F_i$ and
$F_i$ and ![]() $G_i$, respectively for
$G_i$, respectively for ![]() $i=1,2$. Then
$i=1,2$. Then
The next theorem on dispersive ordering between general spacings which is also of independent interest, will be used to prove our main result.
Theorem 3.1. Let ![]() $X_1, \ldots, X_n$ be mutually independent exponential random variables with distinct hazard rates
$X_1, \ldots, X_n$ be mutually independent exponential random variables with distinct hazard rates ![]() $\lambda _1, \ldots, \lambda _n$ and let
$\lambda _1, \ldots, \lambda _n$ and let ![]() $Y_1, \ldots, Y_n$ be a random sample from the exponential distribution with hazard rate
$Y_1, \ldots, Y_n$ be a random sample from the exponential distribution with hazard rate ![]() $\bar \lambda$. Then for
$\bar \lambda$. Then for ![]() $1 \le i \lt j \le n$,
$1 \le i \lt j \le n$,
Proof. Yu [Reference Yu25] proved in Corollary 1 of his paper that for ![]() $1 \le i \lt j \le n$,
$1 \le i \lt j \le n$,
and Kochar and Rojo [Reference Kochar and Rojo14] proved in their Corollary 2.1 that
Xu and Balakrishnan [Reference Xu and Balakrishnan23] proved a special case of the above result when ![]() $i=n$.
$i=n$.
Now, we give the main result of this paper.
Theorem 3.2. Let ![]() $X_1, \ldots, X_n$ be mutually independent exponentials with distinct hazard rates
$X_1, \ldots, X_n$ be mutually independent exponentials with distinct hazard rates ![]() $\lambda _1, \ldots, \lambda _n$ and let
$\lambda _1, \ldots, \lambda _n$ and let ![]() $Y_1, \ldots, Y_n$ form a random sample from the exponential distribution with hazard rate
$Y_1, \ldots, Y_n$ form a random sample from the exponential distribution with hazard rate ![]() $\overline {\lambda } = ( \sum _{i=1}^{n} \lambda _i)/n$. Then, for
$\overline {\lambda } = ( \sum _{i=1}^{n} \lambda _i)/n$. Then, for ![]() $i \in \{2,\ldots,n\}$,
$i \in \{2,\ldots,n\}$,
Proof. It follows from Theorem 3.1 above that for ![]() $2\le i \le n$,
$2\le i \le n$,
Kochar and Korwar [Reference Kochar and Korwar13] proved that ![]() $(X_{i:n} - X_{1:n})$ is independent of
$(X_{i:n} - X_{1:n})$ is independent of ![]() $X_{1:n}$ and
$X_{1:n}$ and ![]() $X_{1:n} \stackrel {st}{=} Y_{1:n}$. Similarly,
$X_{1:n} \stackrel {st}{=} Y_{1:n}$. Similarly, ![]() $(Y_{i:n} - Y_{1:n})$ is independent of
$(Y_{i:n} - Y_{1:n})$ is independent of ![]() $Y_{1:n}$. Moreover,
$Y_{1:n}$. Moreover,
Now, we can express ![]() $X_{i:n}$ and
$X_{i:n}$ and ![]() $Y_{i:n}$ as
$Y_{i:n}$ as
Using (3.4) and the above two equations, it follows from Lemma 3.2 that
This proves the required result.
Remark 3.1. Since the copula of the order statistics of a random sample has the distribution-free property, it is not required that the common hazard rate of ![]() $Y$'s is necessarily
$Y$'s is necessarily ![]() $\bar \lambda$ in the above theorems. In fact, the
$\bar \lambda$ in the above theorems. In fact, the ![]() $Y$'s could be a random sample from any continuous distribution.
$Y$'s could be a random sample from any continuous distribution.
The above theorem can be extended to the PHR model using the technique used in Genest et al. [Reference Genest, Kochar and Xu8].
Theorem 3.3. Let ![]() $X_1,\ldots,X_n$ be independent continuous random variables following the PHR model with
$X_1,\ldots,X_n$ be independent continuous random variables following the PHR model with ![]() $\lambda _1, \ldots, \lambda _n$ as the proportionality parameters. Let
$\lambda _1, \ldots, \lambda _n$ as the proportionality parameters. Let ![]() $Y_1,\ldots,Y_n$ be i.i.d. continuous random variables with common survival function
$Y_1,\ldots,Y_n$ be i.i.d. continuous random variables with common survival function ![]() $\bar {F}^{\bar \lambda }$, then
$\bar {F}^{\bar \lambda }$, then
Proof. Let ![]() $R(t)= - \log \{ {\bar F} (t) \}$ in the PHR model. Make the monotone transformations
$R(t)= - \log \{ {\bar F} (t) \}$ in the PHR model. Make the monotone transformations ![]() $X_i^{*} = R(X_i)$ and
$X_i^{*} = R(X_i)$ and ![]() $Y_i^{*} = - \log \{ {\bar F} (Y_i) \}$. Then, the transformed variable
$Y_i^{*} = - \log \{ {\bar F} (Y_i) \}$. Then, the transformed variable ![]() $X^{*}_i$ has exponential distribution with hazard rate
$X^{*}_i$ has exponential distribution with hazard rate ![]() $\lambda _i$,
$\lambda _i$, ![]() $i=1,\ldots,n$ and
$i=1,\ldots,n$ and ![]() $Y_1^{*}, \ldots, Y_i^{*}$ is a random sample from an exponential distribution with parameter
$Y_1^{*}, \ldots, Y_i^{*}$ is a random sample from an exponential distribution with parameter ![]() ${\bar \lambda }$. Let
${\bar \lambda }$. Let ![]() $X^{*}_{(1)} \lt \cdots \lt X^{*}_{(n)}$ and
$X^{*}_{(1)} \lt \cdots \lt X^{*}_{(n)}$ and ![]() $Y^{*}_{(1)} \lt \cdots \lt Y^{*}_{(n)}$ be the order statistics corresponding to the new sets of variables.
$Y^{*}_{(1)} \lt \cdots \lt Y^{*}_{(n)}$ be the order statistics corresponding to the new sets of variables.
In view of their invariance by monotone increasing transformations of the margins, the copulas associated with the pairs ![]() $(X_{1:n}, X_{n:n})$ and
$(X_{1:n}, X_{n:n})$ and ![]() $(X^{*}_{1:n}, X^{*}_{n:n})$ coincide. Similarly, the pairs
$(X^{*}_{1:n}, X^{*}_{n:n})$ coincide. Similarly, the pairs ![]() $(Y_{1:n}, Y_{n:n})$ and
$(Y_{1:n}, Y_{n:n})$ and ![]() $(Y^{*}_{1:n}, Y^{*}_{i:n})$ have the same copula.
$(Y^{*}_{1:n}, Y^{*}_{i:n})$ have the same copula.
Also, since the more SI dependence ordering is copula-based,
Under the conditions of Theorem 3.3, an upper bound on ![]() $\kappa (X_{1:n}, X_{i:n})$ is given by
$\kappa (X_{1:n}, X_{i:n})$ is given by ![]() $\kappa (Y_{1:n}, Y_{i:n})$. Avérous et al. [Reference Avérous, Genest and Kochar1] obtained an analytic expression for computing the exact values of the Kendall's
$\kappa (Y_{1:n}, Y_{i:n})$. Avérous et al. [Reference Avérous, Genest and Kochar1] obtained an analytic expression for computing the exact values of the Kendall's ![]() $\tau$ for any pair of order statistics from a random sample from a continuous distribution which in our case reduces to
$\tau$ for any pair of order statistics from a random sample from a continuous distribution which in our case reduces to
 $$\tau(Y_{1:n}, Y_{i:n}) = 1-\frac{ 2(n-1)}{2n-1}\left(\begin{array}{c} {n-2}\\ {i-2} \end{array}\right) \sum_{s=0}^{n-i}\left(\begin{array}{c} {n} \\ {s} \end{array}\right) \left/\, \left(\begin{array}{c} {2n-2} \\ {n-i+s} \end{array}\right)\right..$$
$$\tau(Y_{1:n}, Y_{i:n}) = 1-\frac{ 2(n-1)}{2n-1}\left(\begin{array}{c} {n-2}\\ {i-2} \end{array}\right) \sum_{s=0}^{n-i}\left(\begin{array}{c} {n} \\ {s} \end{array}\right) \left/\, \left(\begin{array}{c} {2n-2} \\ {n-i+s} \end{array}\right)\right..$$
Acknowledgments
The author is grateful to the editors and two anonymous referees for their constructive comments and suggestions which led to this improved version of the paper.