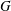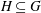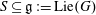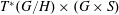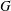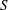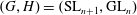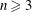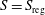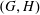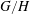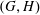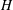This work is concerned with Bielawski’s hyperkähler slices in the cotangent bundles of homogeneous affine varieties. One can associate such a slice with the data of a complex semisimple Lie group 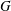$G$, a reductive subgroup 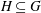$H\subseteq G$, and a Slodowy slice 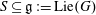$S\subseteq \mathfrak{g}:=\text{Lie}(G)$, defining it to be the hyperkähler quotient of 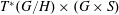$T^{\ast }(G/H)\times (G\times S)$ by a maximal compact subgroup of 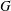$G$. This hyperkähler slice is empty in some of the most elementary cases (e.g., when 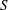$S$ is regular and 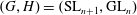$(G,H)=(\text{SL}_{n+1},\text{GL}_{n})$, 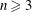$n\geqslant 3$), prompting us to seek necessary and sufficient conditions for non-emptiness.

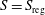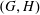We give a spherical-geometric characterization of the non-empty hyperkähler slices that arise when $S=S_{\text{reg}}$ is a regular Slodowy slice, proving that non-emptiness is equivalent to the so-called $\mathfrak{a}$-regularity of $(G,H)$. This $\mathfrak{a}$-regularity condition is formulated in several equivalent ways, one being a concrete condition on the rank and complexity of 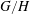$G/H$. We also provide a classification of the $\mathfrak{a}$-regular pairs 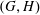$(G,H)$ in which 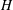$H$ is a reductive spherical subgroup. Our arguments make essential use of Knop’s results on moment map images and Losev’s algorithm for computing Cartan spaces.