Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T01:26:09.861Z Has data issue: false hasContentIssue false
  • English
  • Français

An Application of Spherical Geometry to Hyperkähler Slices

Part of: Special varieties Global differential geometry Linear algebraic groups and related topics

Published online by Cambridge University Press:  24 February 2020

Peter Crooks  and
Maarten van Pruijssen
Peter Crooks
Affiliation:
Department of Mathematics, Northeastern University, 360 Huntington Ave., Boston, MA02115, USA e-mail: [email protected]
Maarten van Pruijssen
Affiliation:
Department of Mathematics, Radboud Universiteit Nijmegen, P.O. Box 9010, 6500 GL Nijmegen, Netherlands e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This work is concerned with Bielawski’s hyperkähler slices in the cotangent bundles of homogeneous affine varieties. One can associate such a slice with the data of a complex semisimple Lie group 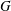$G$, a reductive subgroup 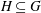$H\subseteq G$, and a Slodowy slice 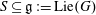$S\subseteq \mathfrak{g}:=\text{Lie}(G)$, defining it to be the hyperkähler quotient of 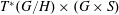$T^{\ast }(G/H)\times (G\times S)$ by a maximal compact subgroup of 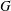$G$. This hyperkähler slice is empty in some of the most elementary cases (e.g., when 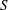$S$ is regular and 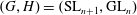$(G,H)=(\text{SL}_{n+1},\text{GL}_{n})$, 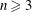$n\geqslant 3$), prompting us to seek necessary and sufficient conditions for non-emptiness.

We give a spherical-geometric characterization of the non-empty hyperkähler slices that arise when 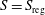$S=S_{\text{reg}}$ is a regular Slodowy slice, proving that non-emptiness is equivalent to the so-called $\mathfrak{a}$-regularity of 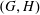$(G,H)$. This $\mathfrak{a}$-regularity condition is formulated in several equivalent ways, one being a concrete condition on the rank and complexity of 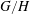$G/H$. We also provide a classification of the $\mathfrak{a}$-regular pairs 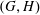$(G,H)$ in which 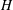$H$ is a reductive spherical subgroup. Our arguments make essential use of Knop’s results on moment map images and Losev’s algorithm for computing Cartan spaces.

Keywords

hyperkähler quotientSlodowy slicespherical geometry

MSC classification

Primary: 20G20: Linear algebraic groups over the reals, the complexes, the quaternions
Secondary: 53C26: Hyper-Kähler and quaternionic Kähler geometry, “special” geometry 14M17: Homogeneous spaces and generalizations
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 3 , June 2021 , pp. 687 - 716
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is supported by the Natural Sciences and Engineering Research Council of Canada [PDF–516638–2018].

References

Abe, H. and Crooks, P., Hessenberg varieties, Slodowy slices, and integrable systems. Math. Z. 291(2019), 1093–1132. https://doi.org/10.1007/s00209-019-02235-7 CrossRefGoogle Scholar
Arzhantsev, I. V. and Chuvashova, O. V., Classification of affine homogeneous spaces of complexity one . Mat. Sb. 195(2004), 3–20. https://doi.org/10.1070/SM2004v195n06ABEH000819 Google Scholar
Avdeev, R. S., Extended weight semigroups of affine spherical homogeneous spaces of nonsimple semisimple algebraic groups. Izv. Ross. Akad. Nauk Ser. Mat. 74(2010), 3–26. https://doi.org/10.1070/IM2010v074n06ABEH002518Google Scholar
Bielawski, R., Hyperkähler structures and group actions . J. London Math. Soc. (2) 55(1997), 400–414. https://doi.org/10.1112/S0024610796004723 CrossRefGoogle Scholar
Bielawski, R., Slices to sums of adjoint orbits, the Atiyah–Hitchin manifold, and Hilbert schemes of points . Complex Manifolds 4(2017), 16–36. https://doi.org/10.1515/coma-2017-0003 CrossRefGoogle Scholar
Biquard, O., Sur les équations de Nahm et la structure de Poisson des algèbres de Lie semi-simples complexes. Math. Ann. 304(1996), 253–276. https://doi.org/10.1007/BF01446293 CrossRefGoogle Scholar
Brion, M., Classification des espaces homogènes sphériques. Compositio Math. 63(1987), 189–208.Google Scholar
Crooks, P., An equivariant description of certain holomorphic symplectic varieties. Bull. Aust. Math. Soc. 97(2018), 207–214. https://doi.org/10.1017/S0004972717001095 CrossRefGoogle Scholar
Crooks, P. and Rayan, S., Abstract integrable systems on hyperkähler manifolds arising from Slodowy slices. Math. Res. Lett. 26(2019), no. 1, 9–33.CrossRefGoogle Scholar
Dancer, A. and Swann, A., Hyperkähler metrics associated to compact Lie groups. Math. Proc. Cambridge Philos. Soc. 120(1996), 61–69. https://doi.org/10.1017/S0305004100074673 CrossRefGoogle Scholar
Dynkin, E. B., Semisimple subalgebras of semisimple Lie algebras. Transl. Ser. 2, Am. Math. Soc. 6(1957), 111–243.Google Scholar
Élašvili, A. G., Canonical form and stationary subalgebras of points in general position for simple linear Lie groups. Funkcional. Anal. i Priložen. 6(1972), 51–62.Google Scholar
Élašvili, A. G., Stationary subalgebras of points of general position for irreducible linear Lie groups . Funkcional. Anal. i Priložen. 6(1972), 65–78.Google Scholar
Hitchin, N. J., The self-duality equations on a Riemann surface . Proc. London Math. Soc. (3) 55(1987), 59–126.CrossRefGoogle Scholar
Hitchin, N. J., Karlhede, A., Lindström, U., and Roček, M., Hyperkähler metrics and supersymmetry . Comm. Math. Phys. 108(1987), 535–589.CrossRefGoogle Scholar
Knop, F., Weylgruppe und Momentabbildung . Invent. Math. 99(1990), 1–23. https://doi.org/10.1007/BF01234409 CrossRefGoogle Scholar
Knop, F., The asymptotic behavior of invariant collective motion . Invent. Math. 116(1994), 309–328. https://doi.org/10.1007/BF01231563 CrossRefGoogle Scholar
Kostant, B., Lie group representations on polynomial rings . Amer. J. Math. 85(1963), 327–404. https://doi.org/10.2307/2373130 CrossRefGoogle Scholar
Kovalev, A. G., Nahm’s equations and complex adjoint orbits . Quart. J. Math. Oxford Ser. (2) 47(1996), 41–58. https://doi.org/10.1093/qmath/47.1.41 CrossRefGoogle Scholar
Krämer, M., Eine Klassifikation bestimmter Untergruppen kompakter zusammenhängender Liegruppen . Comm. Algebra 3(1975), 691–737. https://doi.org/10.1080/00927877508822068 CrossRefGoogle Scholar
Krämer, M., Sphärische Untergruppen in kompakten zusammenhängenden Liegruppen . Compositio Math. 38(1979), 129–153.Google Scholar
Kronheimer, P., A hyperkaḧler structure on the cotangent bundle of a complex Lie group. 1988. arxiv:math/0409253 Google Scholar
Kronheimer, P. B., A hyperkählerian structure on coadjoint orbits of a semisimple complex group. J. London Math. Soc. 42(1990), 193–208.CrossRefGoogle Scholar
Kronheimer, P. B., Instantons and the geometry of the nilpotent variety . J. Differential Geom. 32(1990), 473–490.Google Scholar
Losev, I. V., Calculating Cartan spaces for affine homogeneous spaces . Mat. Sb. 198(2007), 31–56. https://doi.org/10.1070/SM2007v198n10ABEH003889 Google Scholar
Marsden, J. E., Ratiu, T., and Raugel, G., Symplectic connections and the linearisation of Hamiltonian systems . Proc. Roy. Soc. Edinburgh Sect. A 117(1991), 329–380. https://doi.org/10.1017/S030821050002477X CrossRefGoogle Scholar
Mayrand, M., Stratified hyperkähler spaces from semisimple Lie algebras. Transformation Groups, to appear. arxiv:1709.09126 Google Scholar
Mikityuk, I. V., Integrability of invariant Hamiltonian systems with homogeneous configuration spaces . Mat. Sb. (N.S.) 129(1986), no 171, 514–534, 591.Google Scholar
Nakajima, H., Instantons on ALE spaces, quiver varieties, and Kac–Moody algebras . Duke Math. J. 76(1994), 365–416. https://doi.org/10.1215/S0012-7094-94-07613-8 CrossRefGoogle Scholar
Nakajima, H., Quiver varieties and Kac–Moody algebras . Duke Math. J. 91(1998), 515–560. https://doi.org/10.1215/S0012-7094-98-09120-7 CrossRefGoogle Scholar
Panyushev, D. I., Complexity and rank of actions in invariant theory . Algebraic geometry, 8, J. Math. Sci. (New York) 95(1999), 1925–1985. https://doi.org/10.1007/BF02169155 CrossRefGoogle Scholar
Richardson, R. W. Jr., Principal orbit types for algebraic transformation spaces in characteristic zero . Invent. Math. 16(1972), 6–14. https://doi.org/10.1007/BF01391211 CrossRefGoogle Scholar
Tauvel, P. and Yu, R. W. T., Lie algebras and algebraic groups . Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2005.CrossRefGoogle Scholar
Timashev, D. A., Homogeneous spaces and equivariant embeddings . Encyclopaedia of Mathematical Sciences, 138, Invariant Theory and Algebraic Transformation Groups, 8, Springer, Heidelberg, 2011. https://doi.org/10.1007/978-3-642-18399-7 CrossRefGoogle Scholar