1 results
Finite group actions on 4-manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-296
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
-
Let X be a closed, oriented, smooth 4-manifold with a finite fundamental group and with a non-vanishing Seiberg-Witten invariant. Let G be a finite group. If G acts smoothly and freely on X, then the quotient X/G cannot be decomposed as X1#X2 with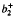
(Xi) > 0, i = 1, 2. In addition let X be symplectic and c1(X)2 > 0 and b+2(X) > 3. If σ is a free anti-symplectic involution on X then the Seiberg-Witten invariants on X/σ vanish for all spinc structures on X/σ, and if η is a free symplectic involution on X then the quotients X/σ and X/η are not diffeomorphic to each other.
(