Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T00:57:56.838Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite group actions on 4-manifolds

Part of: Topological manifolds Differential topology

Published online by Cambridge University Press:  09 April 2009

Yong Seung Cho
Yong Seung Cho
Affiliation:
Department of Mathematics, Ewha Women's University, Seoul 120-750, Korea e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a closed, oriented, smooth 4-manifold with a finite fundamental group and with a non-vanishing Seiberg-Witten invariant. Let G be a finite group. If G acts smoothly and freely on X, then the quotient X/G cannot be decomposed as X1#X2 with 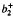(Xi) > 0, i = 1, 2. In addition let X be symplectic and c1(X)2 > 0 and b+2(X) > 3. If σ is a free anti-symplectic involution on X then the Seiberg-Witten invariants on X/σ vanish for all spinc structures on X/σ, and if η is a free symplectic involution on X then the quotients X/σ and X/η are not diffeomorphic to each other.

Keywords

4-manifoldfinite group actionsymplecticspinc structureSeiberg-Witten invariant

MSC classification

Secondary: 57R55: Differentiable structures 57N13: Topology of $E^4$, $4$-manifolds 57S17: Finite transformation groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 66 , Issue 3 , June 1999 , pp. 287 - 296
Copyright
Copyright © Australian Mathematical Society 1999

References

[C1]Cho, Y. S., ‘Finite group actions on the moduli space of self-dual connections (II)’, Michigan Math. J. 37 (1990), 125–132.Google Scholar
[C2]Cho, Y. S., ‘Finite group actions on the moduli space of self-dual connections (I)’, Trans. Amer. Math. Soc. 323 (1991), 233–261.Google Scholar
[C3]Cho, Y. S., ‘Equivariant metrics for smooth moduli spaces’, Topology Appl. 62 (1995), 77–85.CrossRefGoogle Scholar
[C4]Cho, Y. S., ‘Seiberg-Witten invariants on non-symplectic 4-manifolds’, Osaka J. Math. 34 (1997), 169–173.Google Scholar
[C5]Cho, Y. S., ‘Finite group actions on Spinc bundles’, Acta Math. Hungarica, to appear.Google Scholar
[D1]Donaldson, S., ‘Irrationality and the h-cobordism conjecture’, J. Diff. Geom. 26 (1987 a), 14x1–168.Google Scholar
[D2]Donaldson, S., ‘The Seiberg-Witten equations and 4-manifold topology’, Bull. Amer. Math. Soc. (N.S.) 33 (1996), 45–70.CrossRefGoogle Scholar
[FS]Fintushel, R. and Stern, R., ‘An exotic free involution on S 4’, Ann. Math. (2) 113 (1981), 357–365.CrossRefGoogle Scholar
[FM]Friedman, R. and Morgan, J., ‘On the diffeomorphism type of certain algebraic surface I’, J. Diff. Geom. 27 (1988), 297–369.Google Scholar
[G]Gompf, R., ‘A new construction of symplectic manifolds’, Ann. of Math. 142 (1995), 527–595.Google Scholar
[Gr]Gromov, M., ‘Pseudo-holomorphic curves in symplectic manifolds’, Invent. Math. 82 (1985), 307–347.CrossRefGoogle Scholar
[HK1]Hambleton, I. and Kreck, M., ‘Smooth structures on algebraic surfaces with cyclic fundamental group’, Invent. Math. 91 (1988), 53–59.CrossRefGoogle Scholar
[HK2]Hambleton, I. and Kreck, M., ‘Smooth structures on algebraic surfaces with finite fundamental group’, Invent. Math. 102 (1990), 109–114.Google Scholar
[HK3]Hambleton, I. and Kreck, M., ‘Cancellation, elliptic surfaces and the topology of certain four-manifolds’, J. Reine Angew. Math. 444 (1993), 79–100.Google Scholar
[K] D. Kotschick, ‘On irreducible four-manifolds’, preprint.Google Scholar
[KMT]Kotschick, D., Morgan, S. and Taubes, C., ‘Four-manifolds without symplectic structures but with nontrivial Seiberg-Witten invariants’, Math. Res. Lett. 2 (1995), 119–124.CrossRefGoogle Scholar
[KM]Kronheimer, P. and Mrowka, T., ‘The genus of embedded surfaces in the projective plane’, Math. Res. Lett. 1 (1994), 794–808.CrossRefGoogle Scholar
[T1]Taubes, C. H., ‘The Seiberg-Witten invariants and symplectic forms’, Math. Res. Lett. 1 (1994), 809–822.Google Scholar
[T2]Taubes, C. H., ‘The Seiberg-Witten and Gromov invariants’, Math. Res. Lett. 2 (1995), 221–238.Google Scholar
[W1]Wang, S., ‘A vanishing theorem for Seiberg-Witten invariants’, Math. Res. Lett. 2 (1995), 305–311.Google Scholar
[W2]Taubes, C. H., ‘Smooth structures on complex surfaces with fundamental group’, Proc. Amer Math. Soc. 125 (1997), 287–291.Google Scholar
[W]Witten, E., ‘Monopoles and four-manifolds’, Math. Res. Lett. 1 (1994), 769–796.CrossRefGoogle Scholar